图论-最短路算法
1. Floyd算法
- 作用:用于求解多源最短路,可以求解出任意两点的最短路

- 利用动态规划只需三重循环即可(动态规划可以把问题求解分为多个阶段)
- 定义dp[k][i][j]表示点i到点j的路径(除去起点终点)中最大编号不超过k的情况下,点i到点j的最短距离。
- 当加入第k个点作为i到j的中间点:
发现可以使用滚动数组优化第一维度:
枚举所有k,判断是否可以作为中间点,可以作为中间点则优化最短路。
初始化:如果<i, j>无边,则dp[i][j] = INF, 有边则等于边权;dp[i][i] = 0(自己到自己是不用走的)
为了理解更深刻,简单举个例子:
各点之间的关系用邻接矩阵保存(下图中又两个邻接矩阵,一个是两点之间的最短距离,还有一个是两点之间的最短路中经过的节点。)
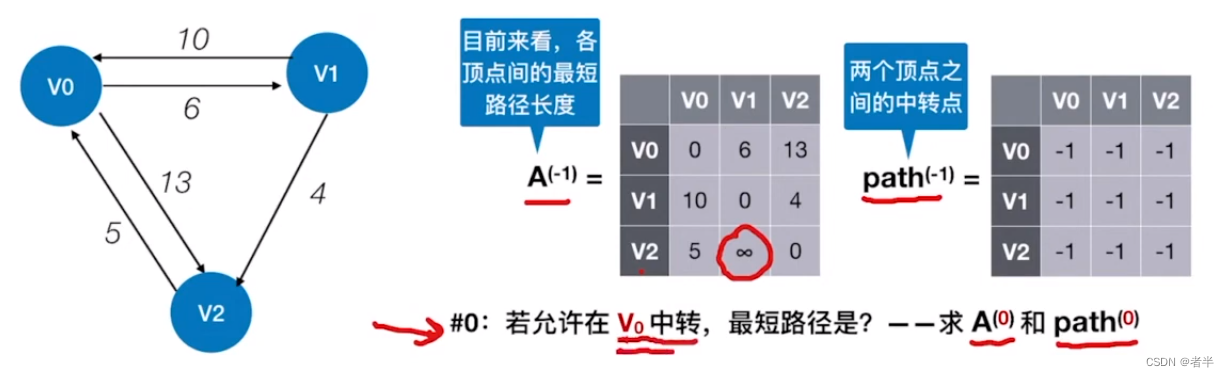

更新
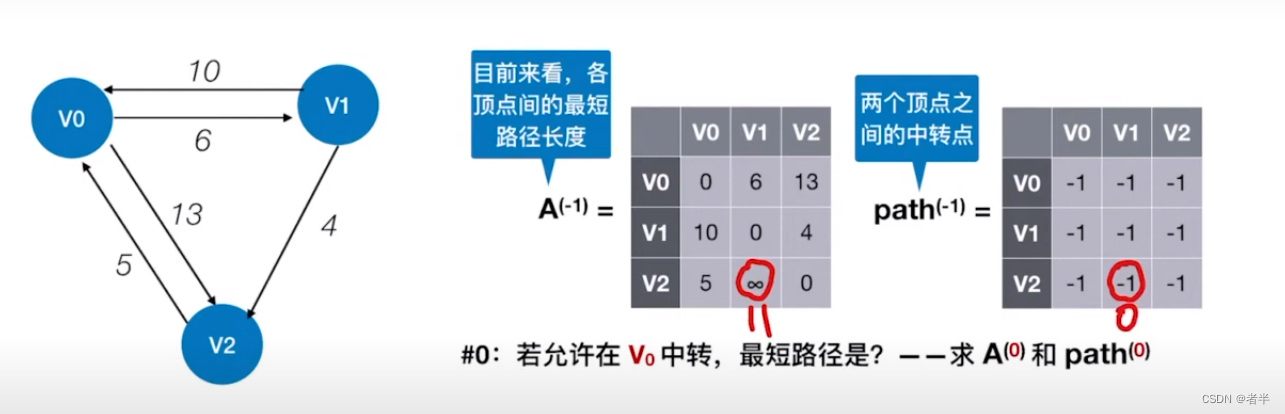
每次基于之前能找到的最短路径,如果比它短就更新。
以2号节点作为中转站是基于1号节点作为中转站的,经过n轮递推就可以得到最终答案(任意两点的最短路)
例题:
蓝桥1121

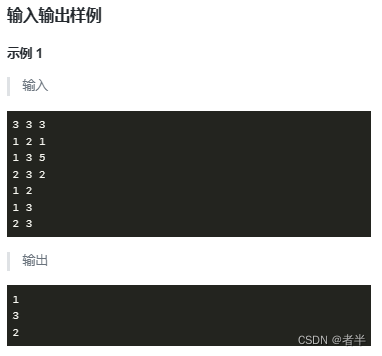
为什么先遍历k,之后遍历i,j?
因为要符合顺序,遍历完中间点后, 就要遍历邻接矩阵,进行最短距离的更新。
import os
import sys# 请在此输入您的代码
n, m, q = map(int, input().split())
INF = 10 ** 18
# dp[i][j]表示i到j的最短路
dp = [[INF] * (n + 1) for i in range(n + 1)] # 初始值设较大值
for i in range(1, n + 1):dp[i][i] = 0 # 自己到自己的距离为0
for _ in range(m):u, v, w = map(int, input().split())dp[u][v] = dp[v][u] = min(dp[u][v], w) # 双向边/无向边(可能有重边)# Floyd算法模板
# dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j])
for k in range(1, n + 1):for i in range(1, n + 1):for j in range(1, n + 1):dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j])for _ in range(q):u, v = map(int, input().split())if dp[u][v] == INF:print(-1)else:print(dp[u][v])蓝桥8336

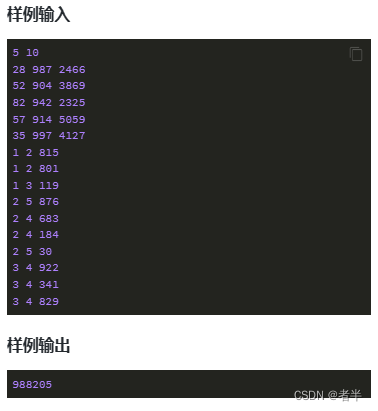
import os
import sys# 请在此输入您的代码
"""
翻译题意:有n个城市,m条边就是有m条路径可以流通,每个城市有自己的商品产出,可以拿去别的地方销售,
需要求出最大利润,但是商品产量ai是不变的,生产成本pi也是不变的,只有售卖单价会随着商品运输到其他
城市会改变,以及带来的运输费用(这里的运输费用有一个路径的问题,需要用最短路算出来最少支付。
"""n, m = map(int, input().split())
# g = s - p - f(路径费用)
INF = 10 ** 17
a, p, s = [0] * (n + 1), [0] * (n + 1), [0] * (n + 1) # 商品的产量, 生产成本, 售卖单价
f = [[INF] * (n + 1) for i in range(n + 1)] # 记录最短路(也就是最短的运输费用)
g = [[0] * (n + 1) for i in range(n + 1)] # 记录利润
for i in range(1, n + 1):a[i], p[i], s[i] = map(int, input().split())
for _ in range(1, m + 1):u, v, w = map(int, input().split())f[u][v] = f[v][u] = min(f[u][v], w)
for i in range(1, n + 1):f[i][i] = 0for k in range(1, n + 1):for i in range(1, n + 1):for j in range(1, n + 1):f[i][j] = min(f[i][k] + f[k][j], f[i][j])
# g[i][j]表示城市1的物品运输到城市j可得的利润=城市j的售价-城市i的成本-运输f[i][j]
for i in range(1, n + 1):for j in range(1, n + 1):g[i][j] = s[j] - p[i] - f[i][j]
ans = 0
for i in range(1, n + 1):# 遍历每个城市的商品now_ans = 0# 遍历移动到的城市(包括自己本身)for j in range(1, n + 1):now_ans = max(now_ans, a[i] * g[i][j])ans += now_ans # 记录每个城市的利润print(ans)总结下解题步骤:
- 初始化邻接矩阵(有边直接连接的直接存,没有的存INF最大值,自己到自己的路径长度为0)
- 遍历(k,i,j)更新i到j的最短路,通过k
- 依据题意更新答案
2. Dijkstra算法
作用:处理非负权边的单源最短路问题
利用贪心+动态规划思想,实现从源点s出发到所有点的最短距离
核心思想:从起点出发,每次选择距离最短的点进行”松弛”操作
算法步骤:
1.将起点入队列,d数组表示从起点s出发到达每个最短距离
2.不断取出队列中距离最小的点u,进行“松弛”:
对于从u到v,权重为w的边
正在更新中...
相关文章:
图论-最短路算法
1. Floyd算法 作用:用于求解多源最短路,可以求解出任意两点的最短路 利用动态规划只需三重循环即可(动态规划可以把问题求解分为多个阶段)定义dp[k][i][j]表示点i到点j的路径(除去起点终点)中最大编号不超…...
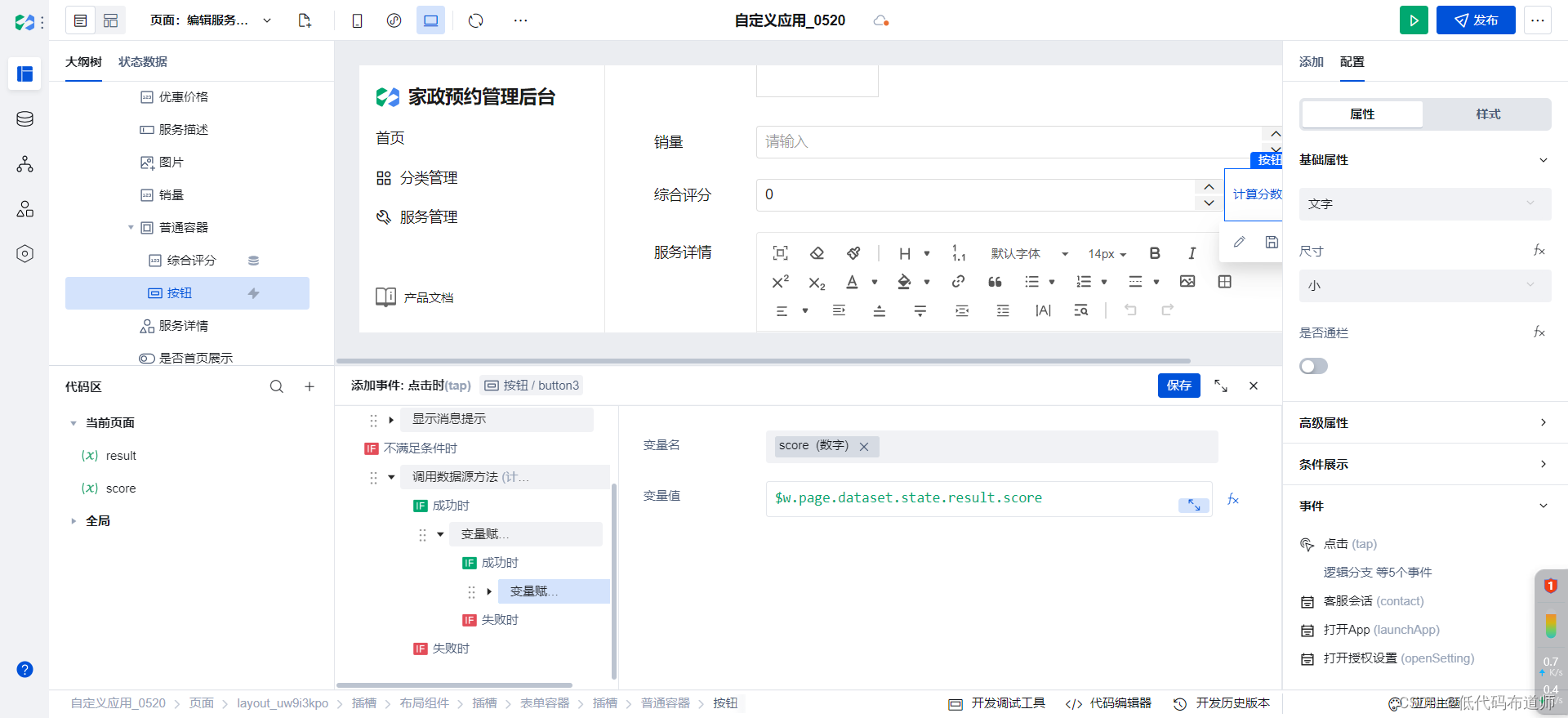
家政预约小程序05服务管理
目录 1 设计数据源2 后台管理3 后端API4 调用API总结 家政预约小程序的核心是展示家政公司提供的各项服务的能力,比如房屋维护修缮,家电维修,育婴,日常保洁等。用户在选择家政服务的时候,价格,评价是影响用…...
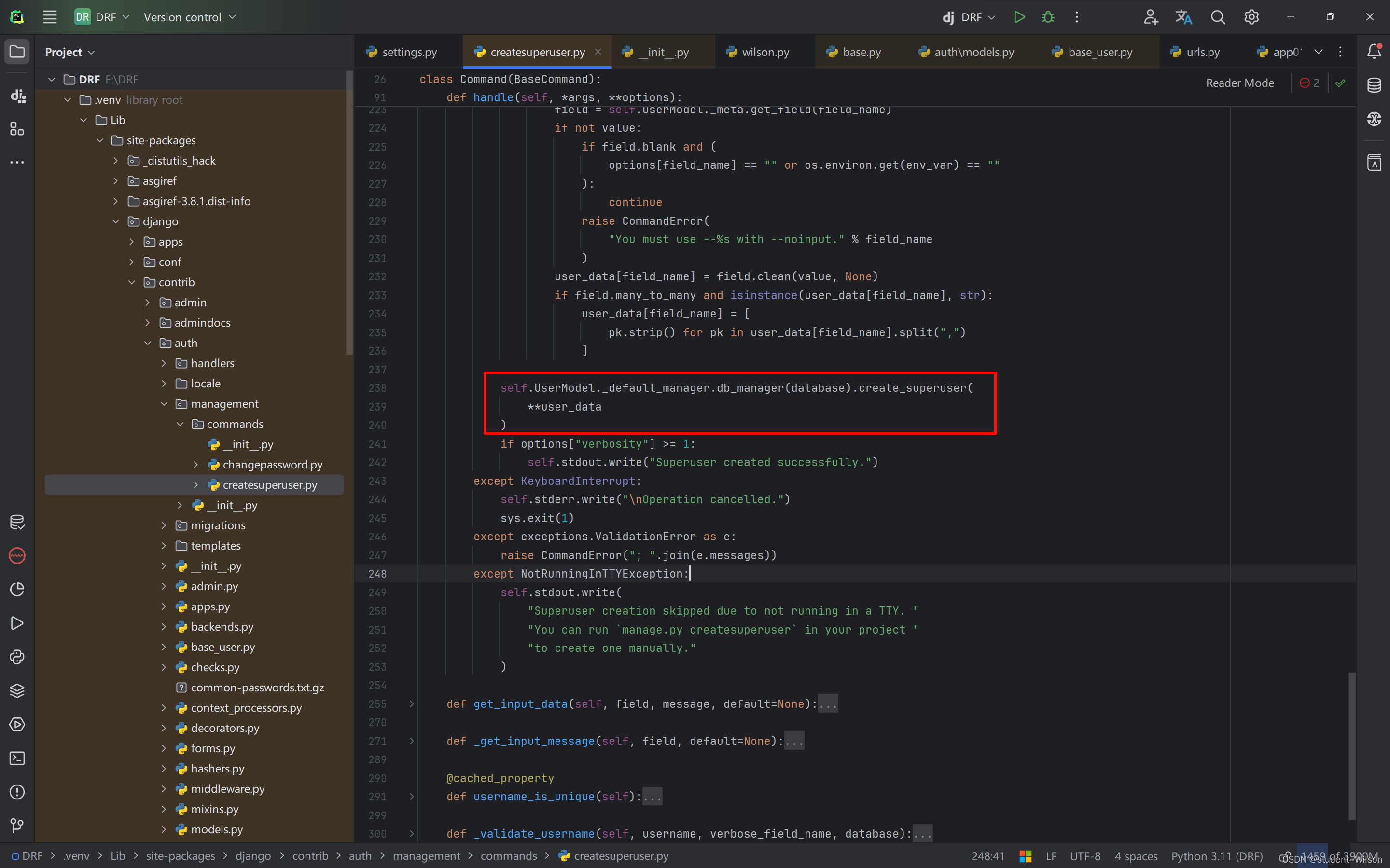
Django自定义命令
Django自定义命令 我们知道,Django内部内置了很多命令,例如 python manage.py runserver python manage.py makemigrations python manage.py migrate我们可以在python控制台中查看所有命令 我们也可以自定义命令,让python manage.py执行…...

详解VLSM技术
在现代网络设计中,如何高效地分配和管理IP地址是一个关键问题。传统的子网划分方法虽然简单,但在实际应用中常常导致IP地址的浪费。为了应对这一问题,VLSM(Variable Length Subnet Mask,可变长子网掩码)技术…...
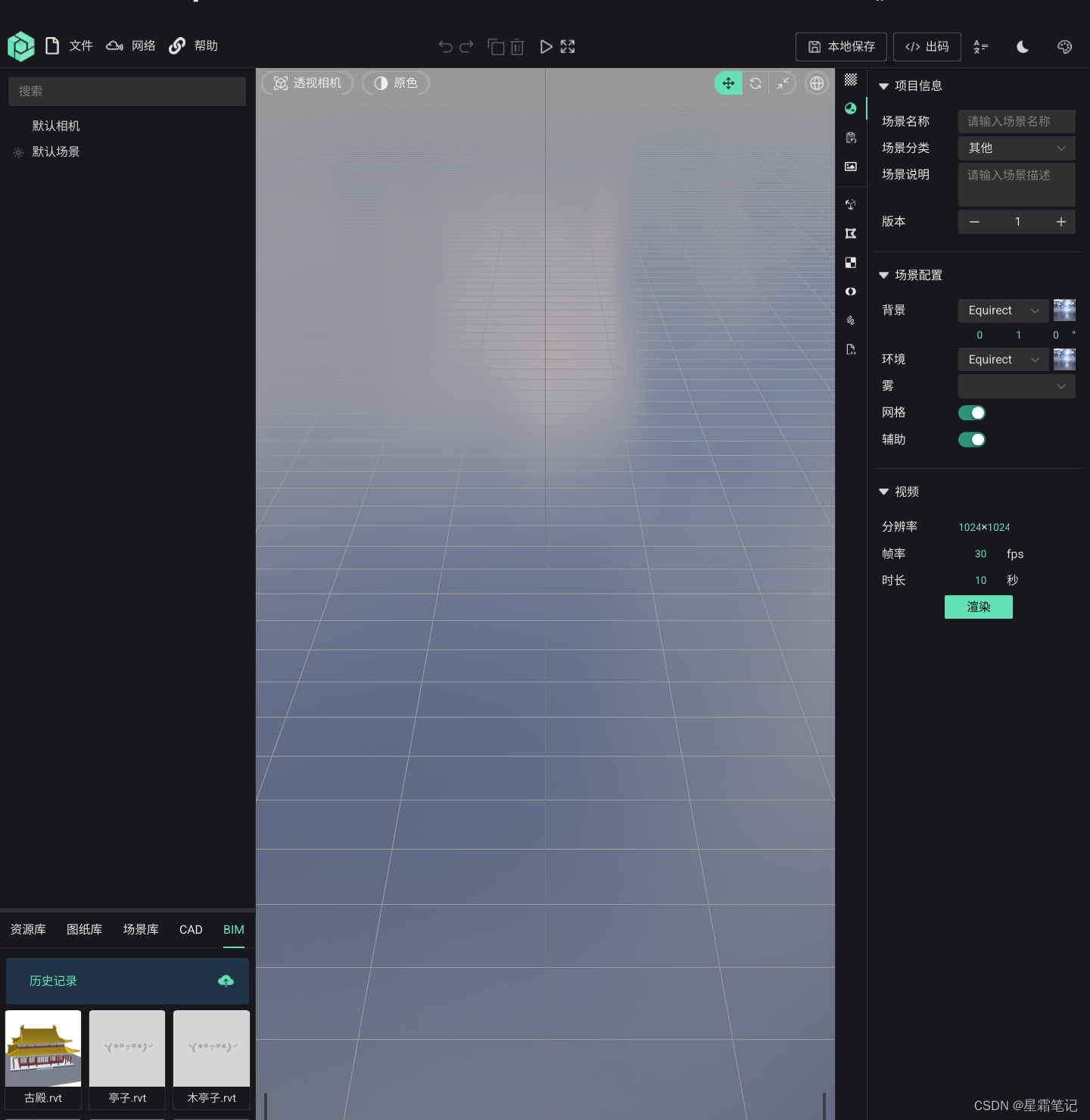
面向浏览器端免费开源的三维可视化编辑器,包含BIM轻量化,CAD解析预览等特色功能。
ES 3DEditor 🌍Github地址 https://github.com/mlt131220/ES-3DEditor 🌍在线体验 https://editor.mhbdng.cn/#/ 基于vue3与ThreeJs,具体查看Doc 主要功能: 模型导入展示,支持OBJ、FBX、GLTF、GLB、RVT、IFC、SEA、3…...
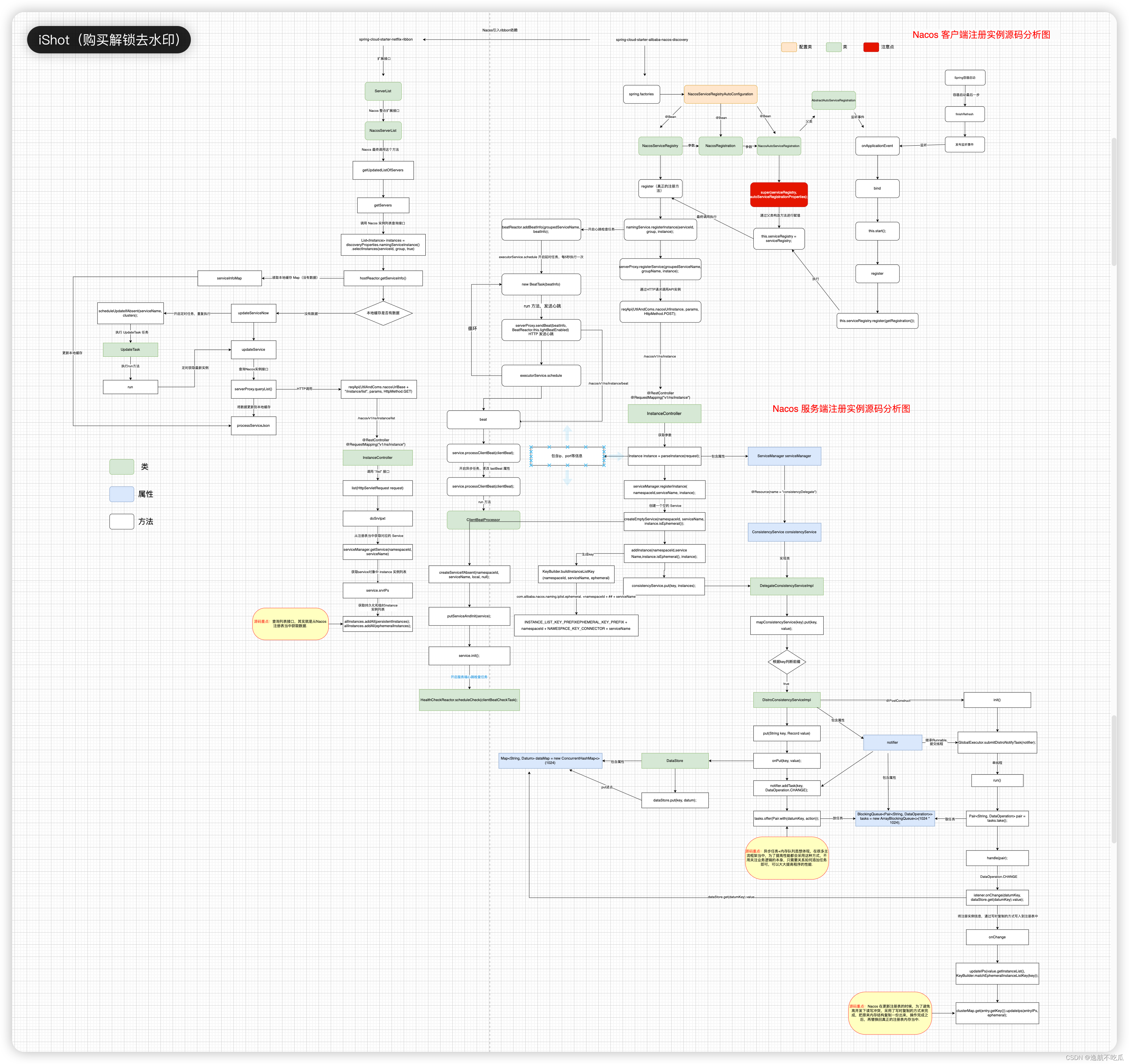
Nacos 进阶篇---Nacos服务端怎么维护不健康的微服务实例 ?(七)
一、引言 在 Nacos 后台管理服务列表中,我们可以看到微服务列表,其中有一栏叫“健康实例数” (如下图),表示对应的客户端实例信息是否可用状态。 那Nacos服务端是怎么感知客户端的状态是否可用呢 ? 本章…...
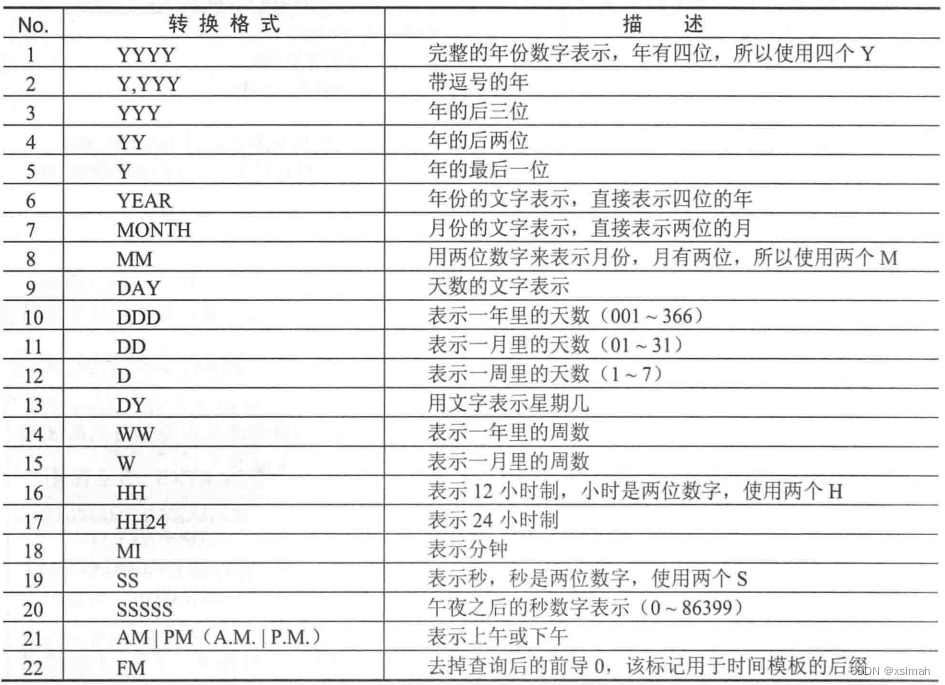
【oracle004】oracle内置函数手册总结(已更新)
1.熟悉、梳理、总结下oracle相关知识体系。 2.日常研发过程中使用较少,随着时间的推移,很快就忘得一干二净,所以梳理总结下,以备日常使用参考 3.欢迎批评指正,跪谢一键三连! 总结源文件资源下载地址&#x…...
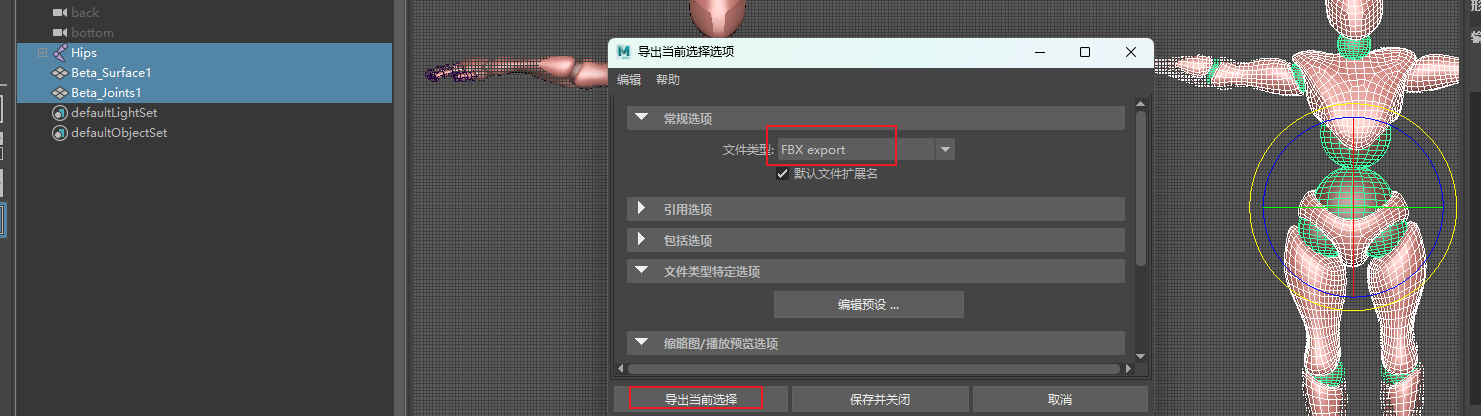
建模:Maya
一、常用按键 1、alt 左键 —— 环绕查看 2、alt 中键 —— 拖动模型所在面板 3、空格 —— 进入三视图模式;空格 左键按住拖动 —— 切换到对应视图 二、骨骼归零 1、T Pose 旋转模式,点击模型,摆好T姿势即可 2、复制模型设置200距离…...
)
持续总结中!2024年面试必问 20 道 Redis面试题(四)
上一篇地址:持续总结中!2024年面试必问 20 道 Redis面试题(三)-CSDN博客 七、Redis过期键的删除策略? Redis 过期键的删除策略主要涉及以下几种方式: 1. 定时删除(Timed Expirationÿ…...

Java中关于List的一些常用操作
先定义一个List,代码如下 //定义一个实例类 public class Model{private String id;private String code;private String name;//setter getter 方法省略}//定义一个List,赋值过程省略 List<Model> list new ArrayList<>();1.将List中每一个对象的id…...

Docker仓库解析
目录 1、Docker仓库类型2、Docker仓库的作用3、工作原理4、管理与使用最佳实践 Docker仓库是Docker生态系统中的重要组成部分,它是用于存储和分发Docker镜像的集中化服务。无论是公共还是私有,仓库都是开发者之间共享和复用容器镜像的基础。 1、Docker仓…...

开发人员容易被骗的原因有很多,涉及技术、安全意识、社会工程学以及工作环境等方面。以下是一些常见原因:
技术方面: 漏洞和补丁管理不当:未及时更新软件和依赖库可能存在已知漏洞,容易被攻击者利用。缺乏安全编码实践:没有遵循安全编码规范,容易引入SQL注入、跨站脚本(XSS)等安全漏洞。错误配置&…...
)
使用Python实现深度学习模型:自动编码器(Autoencoder)
自动编码器(Autoencoder)是一种无监督学习的神经网络模型,用于数据的降维和特征学习。它由编码器和解码器两个部分组成,通过将输入数据编码为低维表示,再从低维表示解码为原始数据来学习数据的特征表示。本教程将详细介…...

数据结构--树与二叉树--编程实现以孩子兄弟链表为存储结构递归求树的深度
数据结构–树与二叉树–编程实现以孩子兄弟链表为存储结构递归求树的深度 题目: 编程实现以孩子兄弟链表为存储结构,递归求树的深度。 ps:题目来源2025王道数据结构 思路: 从根结点开始 结点 N 的高度 max{N 孩子树的高度 1, N兄弟树的…...
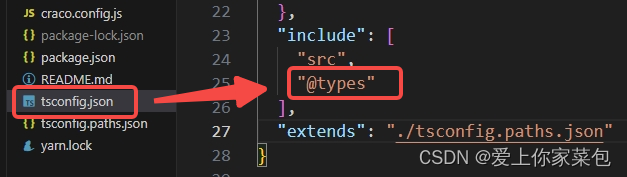
Property xxx does not exist on type ‘Window typeof globalThis‘ 解决方法
问题现象 出现以上typescript警告,是因为代码使用了window的非标准属性,即原生 window 对象上不存在该属性。 解决办法 在项目 根目录 或者 src目录 下新建 xxx.d.ts 文件,然后进行对该 属性 进行声明即可。 注意:假如xxx.d.ts文…...

BOM..
区别:...

rust的版本问题,安装问题,下载问题
rust的版本、安装、下载问题 rust版本问题, 在使用rust的时候,应用rust的包,有时候包的使用和rust版本有关系。 error: failed to run custom build command for pear_codegen v0.1.2 Caused by: process didnt exit successfully: D:\rus…...

SDUT 链表9-------7-9 sdut-C语言实验-约瑟夫问题
7-9 sdut-C语言实验-约瑟夫问题 分数 20 全屏浏览 切换布局 作者 马新娟 单位 山东理工大学 n个人想玩残酷的死亡游戏,游戏规则如下: n个人进行编号,分别从1到n,排成一个圈,顺时针从1开始数到m,数到m的…...

Anthropic绘制出了大型语言模型的思维图:大型语言模型到底是如何工作
今天,我们报告了在理解人工智能模型的内部运作方面取得的重大进展。我们已经确定了如何在 Claude Sonnet(我们部署的大型语言模型之一)中表示数百万个概念。这是对现代生产级大型语言模型的首次详细了解。这种可解释性的发现将来可以帮助我们…...

网络工程师练习题
网络工程师 随着company1网站访问量的不断增加,公司为company1设立了多台服务器。下面是不同用户ping网站www.company1.com后返回的IP地址及响应状况,如图8.58所示。从图8.58可以看出,域名www.company1.com对应了多个IP地址,说明在图8.59所示的NDS属性中启用了循环功能。在…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
