C语言 | Leetcode C语言题解之第108题将有序数组转换为二叉搜索树

题目：

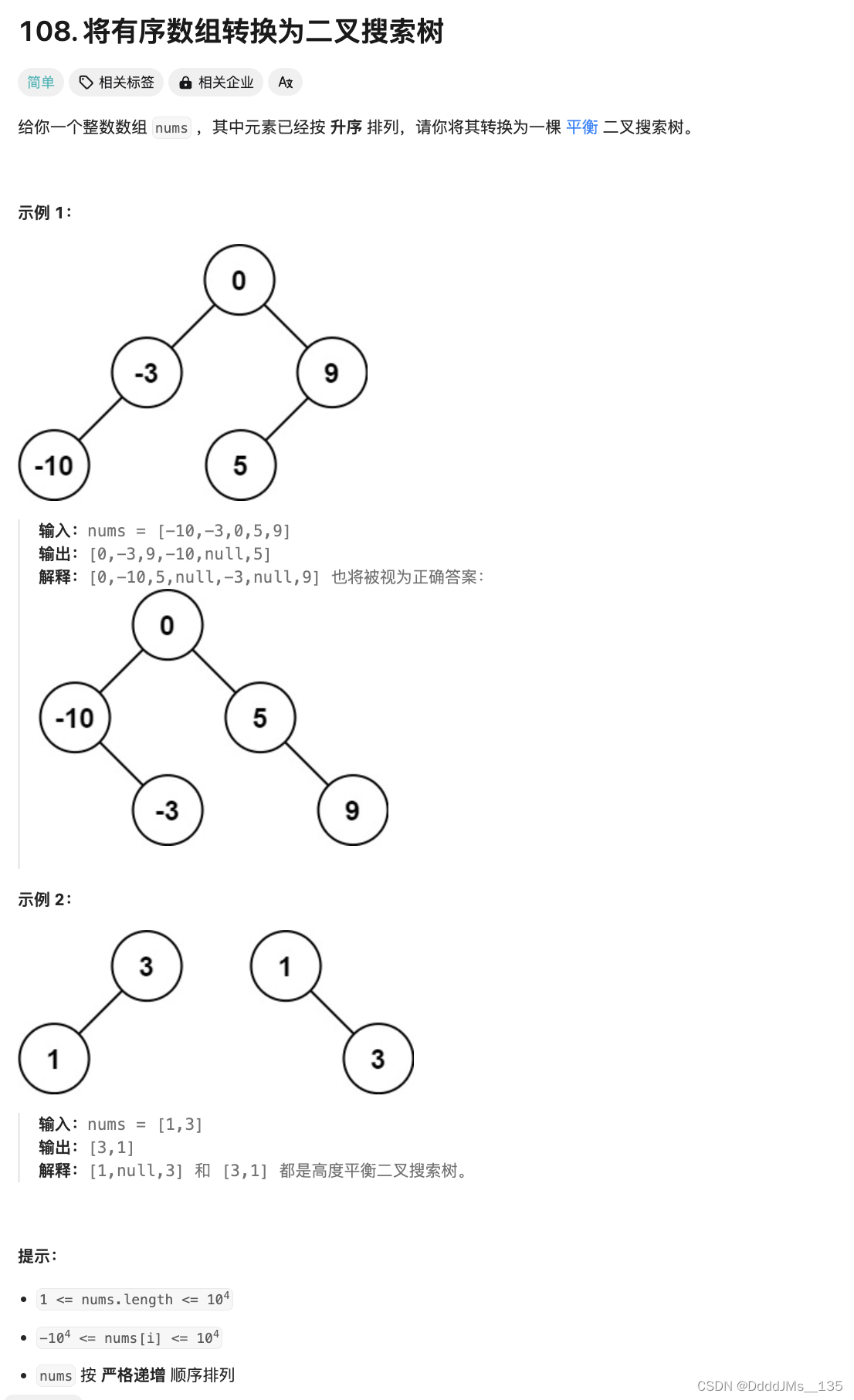
题解：

struct TreeNode* helper(int* nums, int left, int right) {if (left > right) {return NULL;}// 选择任意一个中间位置数字作为根节点int mid = (left + right + rand() % 2) / 2;struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->val = nums[mid];root->left = helper(nums, left, mid - 1);root->right = helper(nums, mid + 1, right);return root;
}struct TreeNode* sortedArrayToBST(int* nums, int numsSize) {return helper(nums, 0, numsSize - 1);
}