「动态规划」按摩师
力扣原题链接,点击跳转。
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列nums,总共有n个预约,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。
我们用动态规划的思想解决这个问题。首先创建dp表,确定状态表示,很自然地想到,可以用dp[i]表示一直收到下标为i的请求后,接受的预约的最长总时长。然而,这么想是不够的,因为对于每个预约,都有可能接受或者不接受。所以要分类讨论:用f[i]表示接受下标为i的请求后,接受的预约的最长总时长;用g[i]表示不接受下标为i的请求后,接受的预约的最长总时长。
接着推导状态转移方程。对于f[i],接受了下标为i的预约,说明没有接受下标为i-1的预约,此时接受的预约的最长总时长应为g[i-1]+nums[i]。对于g[i],不接受下标为i的预约,有可能接受了下标为i-1的预约,也有可能不接受下标为i-1的预约,由于要求最长总时长,所以g[i]=max(f[i-1],g[i-1])。
初始化时,只需把f[0]初始化成nums[0],g[0]初始化成0,再从左往右同时填f表和g表。最后,返回max(f[n-1],g[n-1])。
class Solution
{
public:int massage(vector<int>& nums){int n = nums.size();// 处理边界情况if (n == 0)return 0;// 创建dp表vector<int> f(n);auto g = f;// 初始化f[0] = nums[0];// 填表for (int i = 1; i < n; i++){f[i] = g[i - 1] + nums[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[n - 1], g[n - 1]);}
};相关文章:

「动态规划」按摩师
力扣原题链接,点击跳转。 一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列nums,总共有n个预约,替按摩师找到…...

小程序-滚动触底-页面列表数据无限加载
// index/index.vue <template> <!-- 自定义导航栏 --> <CustomNavbar /> <scroll-view scrolltolower"onScrolltolower" scroll-y class"scroll-view"> <!-- 猜你喜欢 --> <Guess ref"guessRef" /> </s…...
监控上网的软件有哪些?含泪推荐的电脑监控软件
监控上网的软件有很多,企业选择的时候应该遵循什么样的原则呢?鄙人愚见,认为以下四项原则是选择监控软件时首要考虑的。 1、功能需求: 监控软件不应该只是起到控制上网的作用,因为一些泄密行为可能是通过USB接口、打印…...

linux系统防火墙开放端口命令
目录 linux相关命令参考文章1.开放端口1.1 开发单个端口1.2 一次性开放多个端口 2.保存设置3.查看所有开放的端口4.查看防火墙状态 linux相关命令参考文章 管理、设置防火墙规则(firewalld): https://download.csdn.net/blog/column/8489557/137911049 i…...

WebGL渲染引擎优化方向——渲染帧率的优化
作者:caven chen 对此内容感兴趣还可以看前文: WebGL渲染引擎优化方向——加载性能优化 前言 WebGL 是一种强大的图形渲染技术,可以在浏览器中快速渲染复杂的 3D 场景。但是,由于 WebGL 的高性能和高质量要求,如果…...

【文献阅读】ESG评级分化和企业绿色创新
ESG评级分化和企业绿色创新 摘要 (1)本研究通过实证探讨了ESG评级差异是否以及如何影响企业绿色创新。以中国上市公司为样本,我们发现ESG评级差异对企业绿色创新有积极的影响 。经过几次稳健性检查后,该结果仍然成立。 ÿ…...
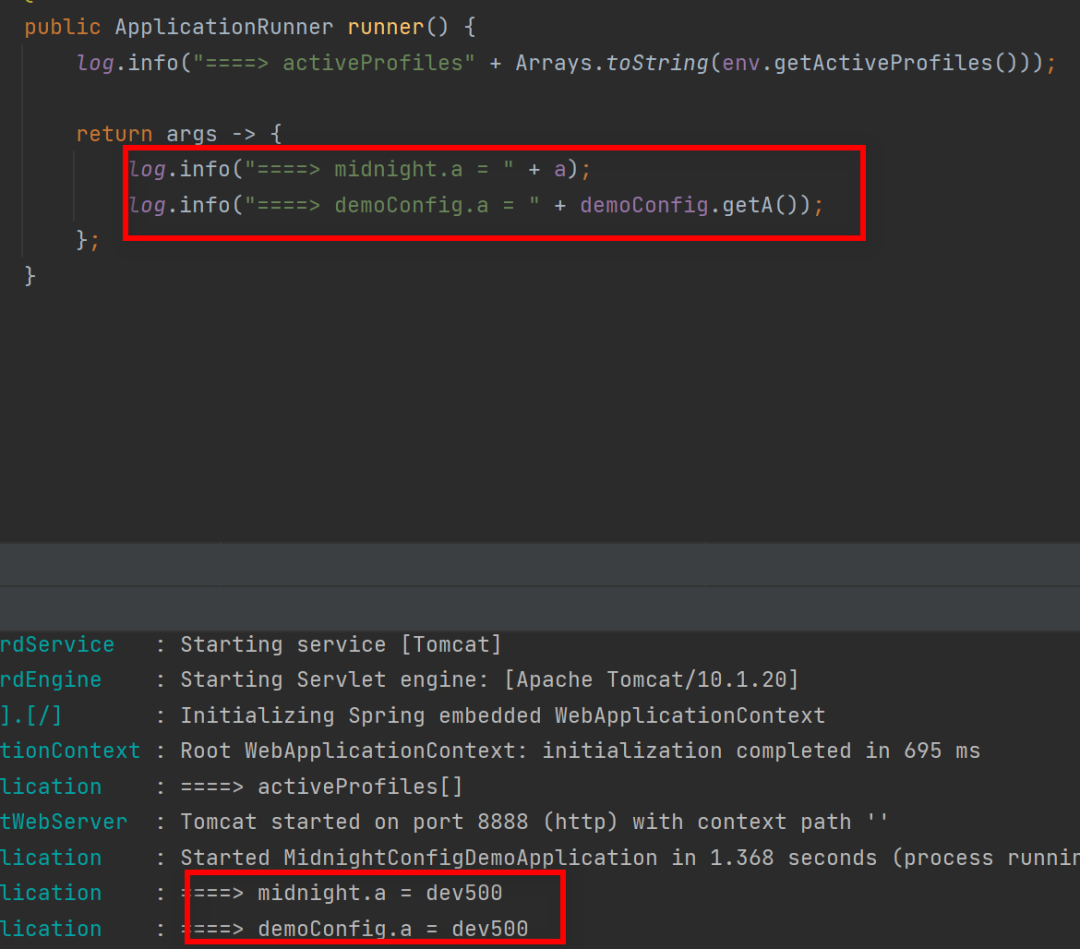
2024-5-6-从0到1手写配置中心Config之实现配置中心客户端
配置加载原理 在Spring中PropertySource类实现了所有属性的实例化。 启动赋值: 定义自定义属性配置源,从config-server获取全局属性;Spring启动时,插入自定义属性配置源;绑定属性会优先使用,给自定义属性…...
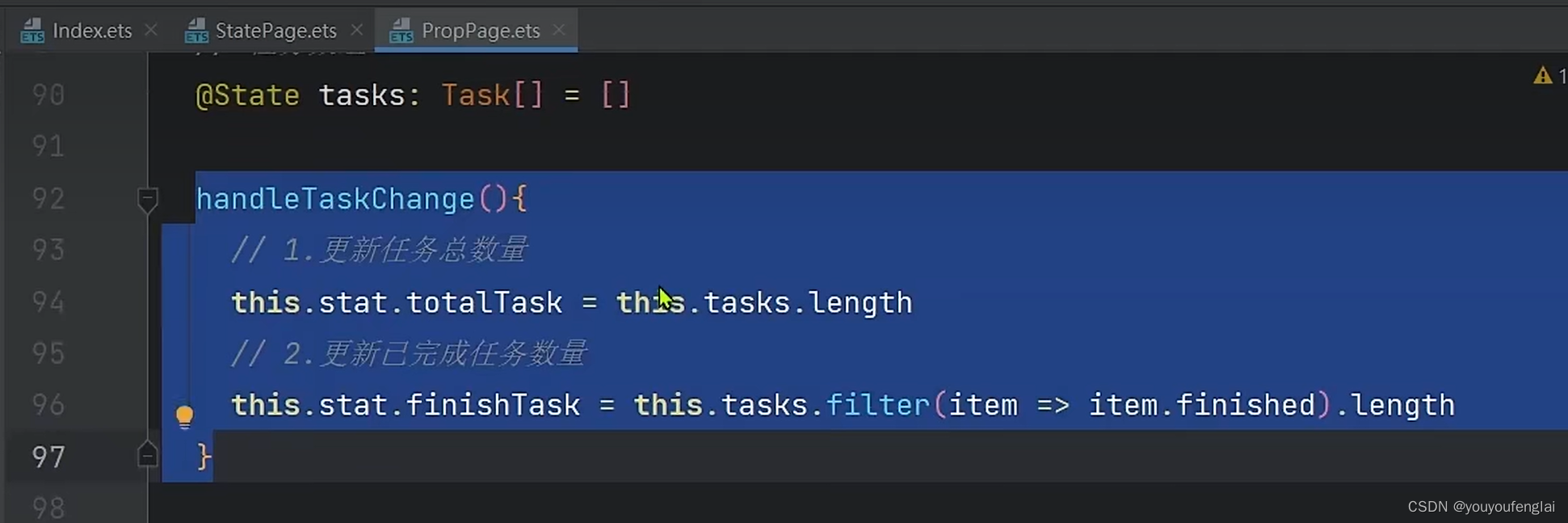
【HarmonyOS4学习笔记】《HarmonyOS4+NEXT星河版入门到企业级实战教程》课程学习笔记(十一)
课程地址: 黑马程序员HarmonyOS4NEXT星河版入门到企业级实战教程,一套精通鸿蒙应用开发 (本篇笔记对应课程第 18 节) P18《17.ArkUI-状态管理Observed 和 ObjectLink》 第一件事:嵌套对象的类型上加上 Observed 装饰器…...
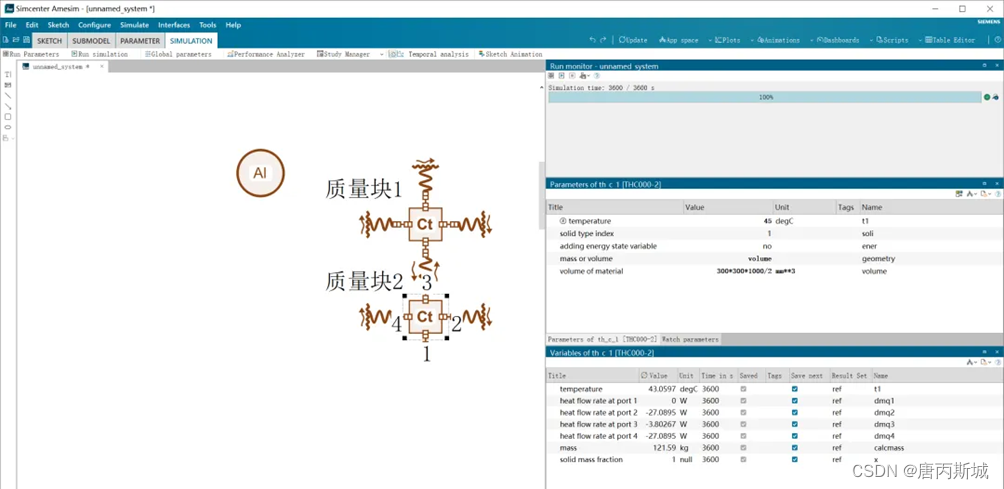
Amesim示例篇-案例1:空间中的铝块散热
前言 本文将通过一个案例继续对Thermal库的元件进一步讲解。 案例1:一个300mm*300mm*1000mm(长*宽*高)的铝板初始温度为45℃,竖直在环境为25℃的空间内静置60min。对流换热系数设置为5W/m2K。本文将通过两种建模方法对铝块的温度…...

深度神经网络——什么是自动编码器?
自动编码器 自动编码器(Autoencoders)是无监督学习领域中一种重要的神经网络架构,它们主要用于数据压缩和特征学习。 自动编码器的定义: 自动编码器是一种无监督机器学习算法,它通过反向传播进行训练,目标…...

初见flyway
flyway (一种数据库版本控制工具 document) 两种文件 V 和 R V: V 开头是不可重复执行的文件,每次修改完都该更改名称 R: R 开头是可重复执行的文件,需要保证内部sql都是可以重复执行的 名称格式: V__table_name.sql, R__table_name.sql …...
)
9.6 Go语言入门(数组、切片和指针)
Go语言入门(数组、切片和指针) 目录五、数组、切片和指针1. 数组1.1 声明和初始化数组1.2 访问和修改数组元素1.3 多维数组 2. 切片2.1 声明和初始化切片2.2 访问和修改切片元素2.3 切片操作2.4 切片的追加和拷贝 3. 指针3.1 声明和初始化指针3.2 指针与…...
)
Web面试题(一)
一:以前公司的测试流程? (1)问题分析 面试官主要为了考察候选者对软件测试流程的理解和掌握程度。 (2)核心答案讲解 1)需求分析与评审 2ÿ…...
【Crypto】一眼就解密
文章目录 前言一眼就解密解题感悟 前言 Basic写累了,写写别的 一眼就解密 一眼md5试一试 小小flag 拿下! 解题感悟 30秒搞定...
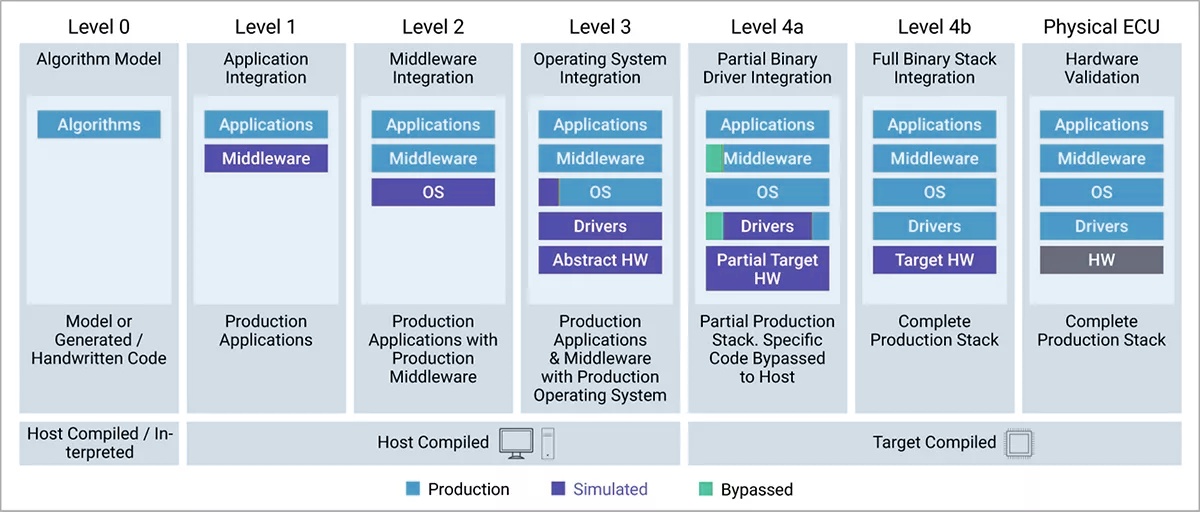
虚拟ECU:彻底改变汽车软件开发与测试
汽车开发领域有着垂直性较强的一系列需求,其中最为瞩目的需求之一就是对安全高效的软件测试方法的需求。传统的汽车开发偏向使用硬件原型与真实ECU进行软件测试,但由于硬件设备往往在开发周期的中后阶段才生产完成,给汽车开发带来了成本与时间…...
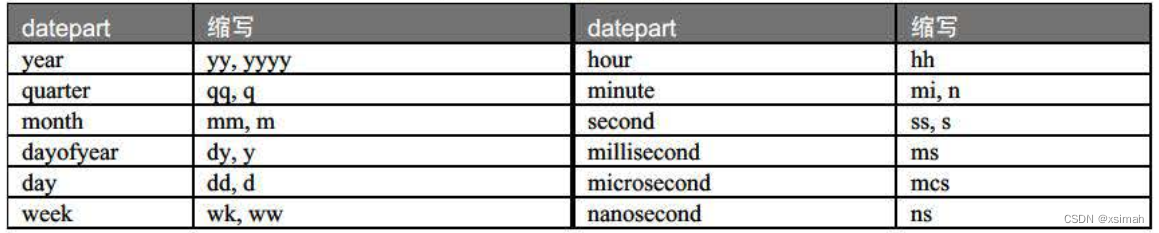
【SQL Server001】SQLServer2016常用函数实战总结(已更新)
1.熟悉、梳理、总结下SQL Server相关知识体系。 2.日常研发过程中使用较少,随着时间的推移,很快就忘得一干二净,所以梳理总结下,以备日常使用参考 3.欢迎批评指正,跪谢一键三连! 总结源文件资源下载地址&am…...

51单片机简单控制180度舵机
代码: 链接:https://pan.baidu.com/s/1K9dg2NwRhy49db_O_hqv-g?pwd1234 提取码:1234 一、路线 我在了解这个舵机之前最像想看到的是一个完全的路径。 比如我想学习b站上那个智能门锁,那就得每个模块的基本代码都会才能结合各…...

PCL 常用小知识
文章目录 一、时间计算二、实现类似`pcl::PointCloud::Ptr`和`pcl::PointCloud`的两个类相互转换三、查找点云的x,y,z的极值四、知道需要保存点的索引,从原点云中拷贝点到新点云五、从点云里删除和添加点六、对点云进行全局或局部变换七、链接两个点云字段(两点云大小必须相…...
)
rbd块设备数据IO流程(client端)
一、rbd内核驱动写入流程 1)初始化 首先是rbd驱动的初始化工作:包括验证libceph的兼容性,分配内存,在sysfs中创建块设备控制文件、创建工作队列rbd_wq并调用INIT_WORK初始化它 module_init(rbd_init); static int __init rbd_i…...

数据仓库、数据中台、大数据平台之间的关系
数据行业经常会出现数据仓库、数据中台、大数据平台等概念,容易产生疑问,它们中间是相等,还是包含的关系? 数据中台和数据仓库概念的关系 数据中台概念是包含数据仓库的,数据仓库是数据中台中的一部分,包含…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
