交换排序、归并排序、计数排序
冒泡排序:
void BubbleSort(int* a, int n)
{//第一层循环是趟数,第二层是交换for (int i = 0; i <= n-2; i++){int flag = 0;for (int j = 0; j <= n - 2 - i; j++){if (a[j] > a[j + 1]){swap(&a[j], &a[j + 1]);flag = 1;}}if (flag == 0){break;}
}
}这里做了一个小优化,通过flag的值来减少运行趟数,防止已经有序的情况下继续比较,最坏时间复杂度N方,最好时间复杂度o(N) ,具有稳定性
快速排序:
void _QuickSort1(int* a, int left, int right)
{int key = left; int begin = left, end = right;if (begin >=end){return;}三数取中法//int mid =Getmid(a, left, right);//swap(&a[left], &a[mid]);//随机数法//int randi = rand() % (right - left) + left;//swap(&a[randi], &a[left]);while (begin<end){while (begin<end){if (a[key] <= a[end])//一定保证右边先走{end--;}else{break;}}while (begin<end){if (a[key] >=a[begin]){begin++;}else{break;}}swap(&a[begin], &a[end]);}swap(&a[left], &a[begin]);key = begin;_QuickSort1(a, 0, key - 1);_QuickSort1(a, key + 1, right);
}快排时间复杂度是o(nlogn),但是当整个数组为有序序列时,快排时间复杂度就为N方,所以这里有三数取中法和随机数法, 使key的值变得随机,这里更推荐三数取中,因为交换后所得到的值肯定为中间值,但有一种特殊情况,就是整个数列中的数都为同一个值,这时候时间复杂度只能为N方,具有不稳定性
三数取中法
int Getmid(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] > a[mid]){if (a[mid] > a[right]) {return mid;}else if (a[left] > a[right]){return right;}else{return left;}}else{if (a[left] > a[right]){return left;}else if (a[right] < a[mid]){return right;}else{return mid;}}
}随机数法
//随机数法//int randi = rand() % (right - left) + left;快排双指针法:
void _QuickSort2(int* a, int left, int right)
{if (left >= right){return;}int key = left;int prev = left;int cur = left+1;while (cur <= right){if (a[cur] < a[key] && ++prev != cur){swap(&a[prev], &a[cur]);}cur++;}swap(&a[key], &a[prev]);key = prev;_QuickSort2(a, 0, key - 1);_QuickSort2(a, key + 1, right);
}相比最原始的快排更好理解,代码量也少
快排非递归
void _QuickSort(int* a, int n)
{ST st;STInit(&st);STPush(&st, n-1);STPush(&st, 0);while (!STEmpty(&st)){int left = STTop(&st);STPop(&st);int right = STTop(&st);STPop(&st);int key = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[key] && ++prev != cur){swap(&a[prev], &a[cur]);}cur++;}swap(&a[key], &a[prev]);key = prev;if ((key+1)<right){STPush(&st, right);STPush(&st, key + 1);}if (left<(key-1)){STPush(&st, key - 1);STPush(&st, left);}}STDestroy(&st);
}当递归次数太多时会建立大量函数栈帧,所以在这里实现快排的非递归排序,这里用到了栈的知识 ,模拟了快排的递归过程,类似于二叉树的前序遍历,运用队列也可以实现,但队列是模拟了二叉树的层序遍历,快排的本质还是前序遍历
归并排序:
void _MergeSort(int* a, int left, int right,int*tem)
{if (left>= right){return;}int mid = (left + right) / 2;int begin1 = left;int end1 = mid;int begin2 = mid + 1;int end2 = right;_MergeSort(a, left, mid, tem);_MergeSort(a, mid + 1, right, tem);int i = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tem[i++]=a[begin1++];}else{tem[i++] = a[begin2++];}}while (begin1 <= end1){tem[i++] = a[begin1++];}while (begin2 <= end2){tem[i++] = a[begin2++];}memcpy(a + left, tem + left,sizeof(int)*( right - left + 1));
}时间复杂度nlogn,具有稳定性
归并排序的非递归
void _MergeSort1(int* a, int n)
{int* tem = (int*)malloc(sizeof(int) * n);if (tem == NULL){perror("malloc fail");return;}int gap = 1;//gap是每组长度,长度等于n的时候不用归并,理解本质while (gap < n){for (int i = 0; i <n; i+=2*gap){int left = i;int right = i + 2 * gap - 1;int begin1 = i;int end1 = i + gap - 1;int begin2 = end1 + 1;int end2 = begin2 + gap - 1;int j = begin1;if (end1 >= n-1 || begin2 >= n){break;}if (end2 >=n){end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tem[j++] = a[begin1++];}else{tem[j++] = a[begin2++];}}while (begin1 <= end1){tem[j++] = a[begin1++];}while (begin2 <= end2){tem[j++] = a[begin2++];}memcpy(a + left, tem + left, sizeof(int) * (end2 - left + 1));//end2可能会变,这里不能用right减}gap *= 2;}free(tem);tem = NULL;
}计数排序
void CountSort(int* a, int n)
{int min = a[0], max =a[ 0];for (int i = 1; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}int range = max - min + 1;int* count = (int*)calloc(sizeof(int),range);if (count == NULL){return;}for (int i = 0; i < n; i++){count[a[i]-min]++;//出现几次}int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}
}时间复杂度o(n+range),空间复杂度 o(range),比较适合处理相对集中的数据,计数排序只能对整数排序,所以这里不讨论其稳定性
相关文章:

交换排序、归并排序、计数排序
冒泡排序: void BubbleSort(int* a, int n) {//第一层循环是趟数,第二层是交换for (int i 0; i < n-2; i){int flag 0;for (int j 0; j < n - 2 - i; j){if (a[j] > a[j 1]){swap(&a[j], &a[j 1]);flag 1;}}if (flag 0){break;…...

怎么查看 iOS ipa包 mobileprovision 改动
查看 iOS .ipa 包中的 .mobileprovision 文件(即配置文件或描述文件)的改动,可以通过以下步骤进行: 重命名 .ipa 文件:将 .ipa 文件扩展名改为 .zip。例如,如果文件名为 MyApp.ipa,则重命名为 M…...

【Unitydemo制作】音游制作—控制器与特效
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:就业…...

[程序员] 最近的感悟,错误处理占大头?
根据昨天分享的一个问题,想到的。 在代码里,异常处理的代码也算是占大头,扑面而来的就是发生错误时怎么处理的大片代码;而且出现问题的概率是绝对的占大头。所以,异常代码出现bug的概率也在不知不觉中增加!…...
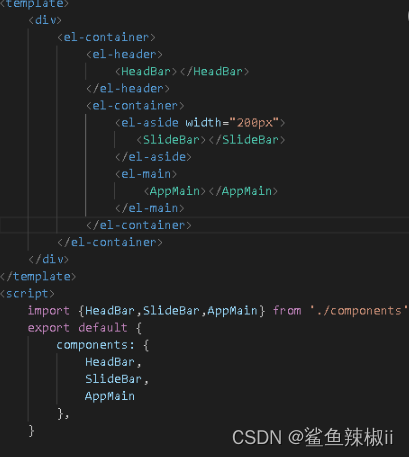
vue3(一) - 结构认识
通过之前博客应该已经完成了vue脚手架的认识和创建(地址),这节我们简单介绍一下需要使用的一些关键技术,后续在详细介绍 结构目录 创建脚手架时,我选择了TypeScript,store,route这三个选项 index.html入口 node_mo…...
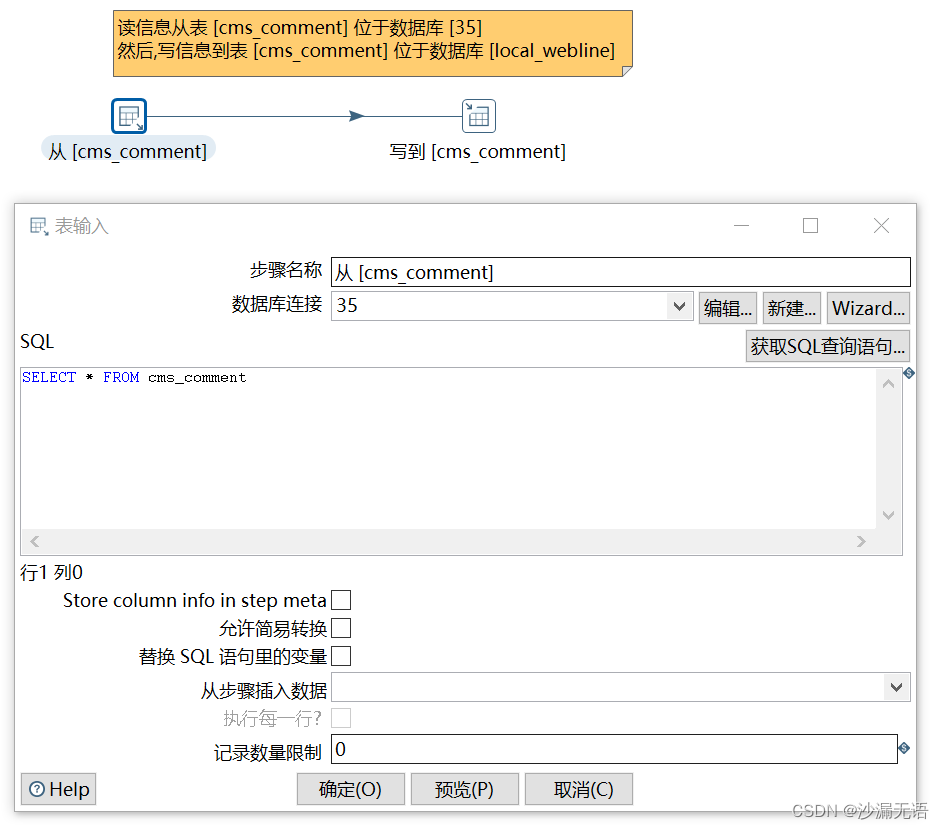
数据库迁移——kettle开发01
背景:数据库的多种多样,在搭建项目之初,并没有详细考虑到数据库的建设,当增加配置不能满足业务场景需要时,这时候考虑到使用更高性能的数据库,如将MySQL更换为oracle数据库。或者在搭建新项目时,…...

Netty: Netty中的组件
文章目录 一、EventLoop1、EventLoop2、EventLoopGroup(1)处理普通时间和定时任务(2)处理IO任务 二、Channel三、Future&Promise四、Handler&Pipeline五、ByteBuf 一、EventLoop 1、EventLoop EventLoop本质是一个单线程…...

Julia编程01:Julia语言介绍
在2020上半年,因为疫情无法返校,所以在家待了半年,期间学习一点了R语言、Python、Julia、linux和C语言,只是学习基础语法并没有项目练习,因此返校半年后差不多都不记得了,现在重新捡起Julia丰富下当时写的笔…...
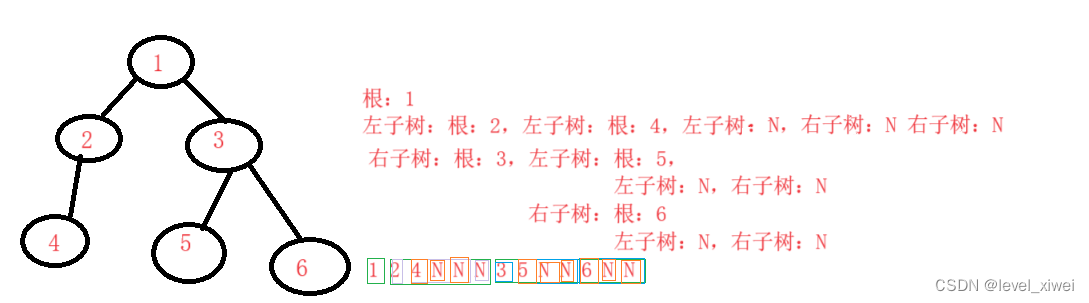
二叉树顺序结构及链式结构
一.二叉树的顺序结构 1.定义:使用数组存储数据,一般使用数组只适合表示完全二叉树,此时不会有空间的浪费 注:二叉树的顺序存储在逻辑上是一颗二叉树,但是在物理上是一个数组,此时需要程序员自己想清楚调整…...

【Python】pandas连续变量分箱
路过了学校花店 荒野到海边 有一种浪漫的爱 是浪费时间 徘徊到繁华世界 才发现你背影 平凡得特别 绕过了城外边界 还是没告别 爱错过了太久 反而错得完美无缺 幸福兜了一个圈 🎵 林宥嘉《兜圈》 import pandas as pd import numpy as np from sklearn.model_selecti…...

Qt 打卡小程序总结
1.Qt::Alignment(枚举类型)用于指定控件或文本的对齐方式 Qt::AlignLeft:左对齐。Qt::AlignRight:右对齐。Qt::AlignHCenter:水平居中对齐。Qt::AlignTop:顶部对齐。Qt::AlignBottom:底部对齐。…...

【qt】标准项模型
标准项模型 一.使用标准型项模型1.应用场景2.界面拖放3.创建模型4.配套模型5.视图设置模型6.视图属性的设置 二.从文件中拿到数据1.文件对话框获取文件名2.创建文件对象并初始化3.打开文件对象4.创建文本流并初始化5.读取文本流6.关闭文件7.完整代码 三.为模型添加数据1.自定义…...
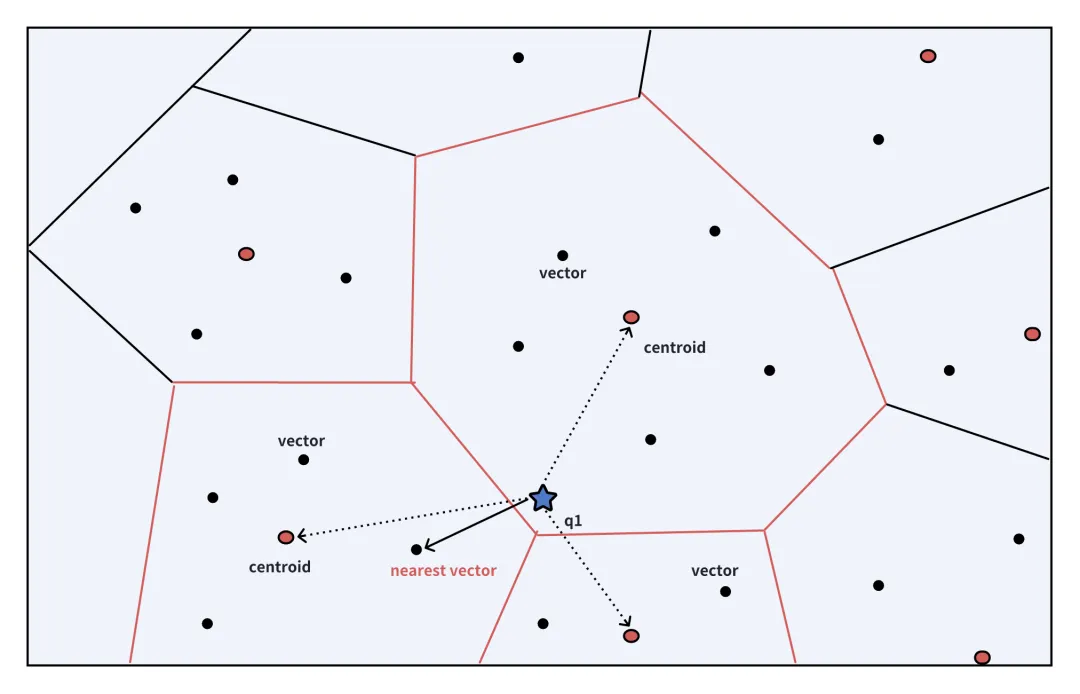
一文深度剖析 ColBERT
近年来,向量搜索领域经历了爆炸性增长,尤其是在大型语言模型(LLMs)问世后。学术界开始重点关注如何通过扩展训练数据、采用先进的训练方法和新的架构等方法来增强 embedding 向量模型。 在之前的文章中,我们已经深入探…...
css左右滚动互不影响
想实现左右都可以滚动,且互不影响。 只需要再左边的css里面 .threedlist {cursor: pointer;width: 280px;position: fixed;height: 100vh; /* 定义父容器高度 */overflow-y: auto; /* 只有在内容超过父容器高度时才出现滚动条 */} 如果想取消滚动条样式 .threedli…...

【linux-uboot移植-mmc及tftp启动-IMX6ULL】
目录 1. uboot简介2. 移植前的基本介绍:2.1 环境系统信息: 3. 初次编译4. 烧录编译的u-boot4.1 修改网络驱动 5. 通过命令启动linux内核5.1 通过命令手动启动mmc中的linux内核5.1.1 fatls mmc 1:15.1.2 fatload mmc 1:1 0x80800000 zImage5.1.3 fatload mmc 1:1 0x8…...
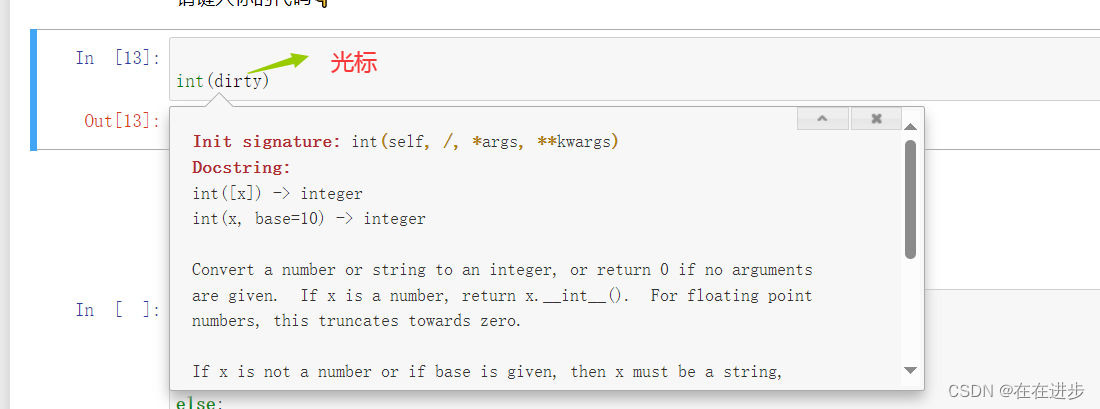
Python-温故知新
1快速打开.ipynb文件 安装好anaconda后,在需要打开notebook的文件夹中, shift键右键——打开powershell窗口——输入jupyter notebook 即可在该文件夹中打开notebook的页面: 2 快速查看函数用法 光标放在函数上——shift键tab 3......

绿联NAS DXP系列发布:内网穿透技术在私有云的应用分析
5月23日,绿联科技举行了“新一代存储方式未来已来”发布会,发布了绿联NAS私有云DXP系列(包括两盘位到八盘位的九款新品)以及由绿联科技自研的全新NAS系统UGOS Pro。此次绿联发布的DXP系列九款产品,共有两盘位、四盘位、…...

力扣:242. 有效的字母异位词
242. 有效的字母异位词 给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。 注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。 示例 1: 输入: s "anagram", t "nagaram"…...
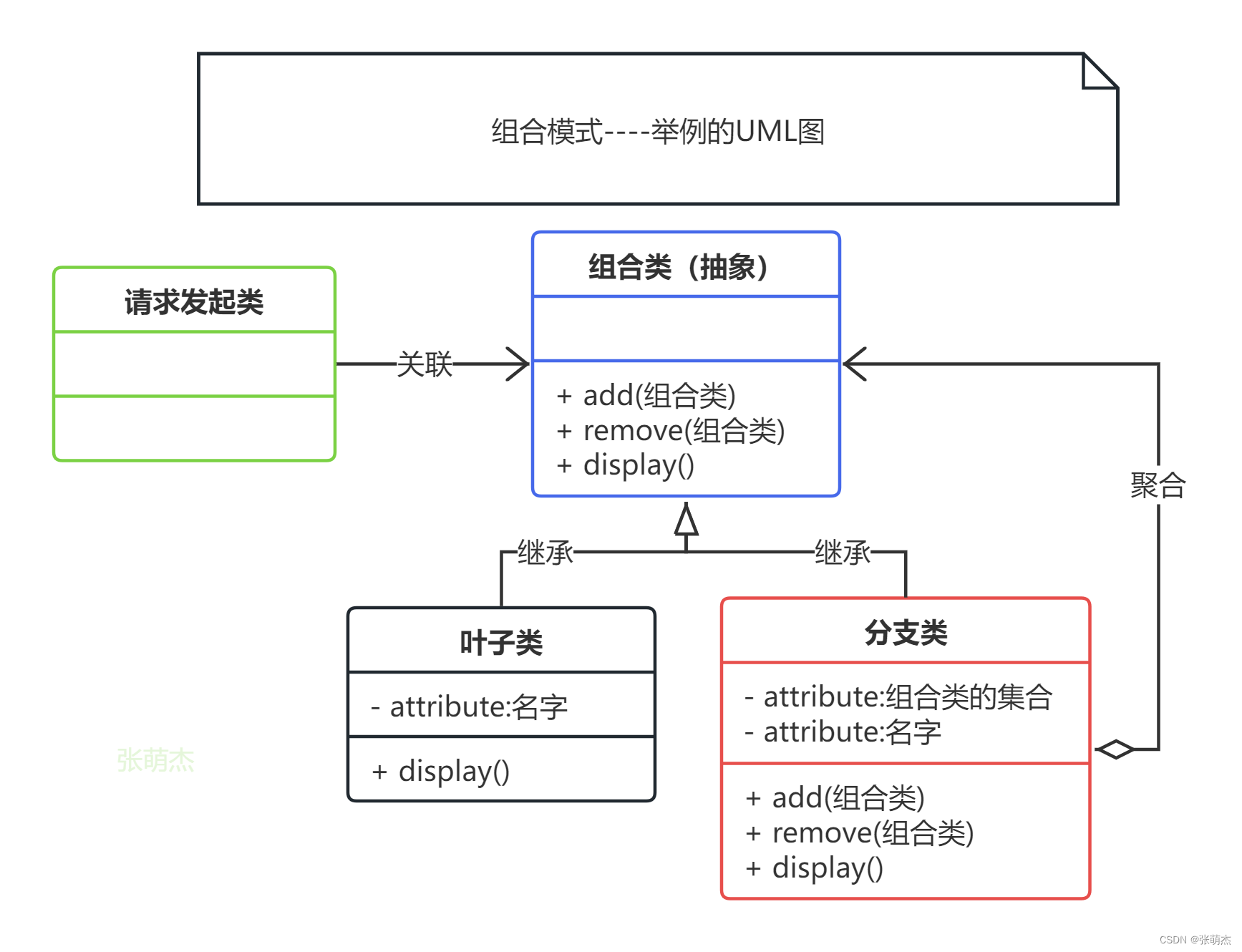
设计模式14——组合模式
写文章的初心主要是用来帮助自己快速的回忆这个模式该怎么用,主要是下面的UML图可以起到大作用,在你学习过一遍以后可能会遗忘,忘记了不要紧,只要看一眼UML图就能想起来了。同时也请大家多多指教。 组合模式(Composit…...
)
MyBatis面试题(Mybaits的优点、缺点、适用场合、与Hibernate有哪些不同)
一、Mybaits的优点: 1、基于 SQL 语句编程,相当灵活,不会对应用程序或者数据库的现有设计造成任 何影响,SQL 写在 XML里,解除 sql与程序代码的耦合,便于统一管理;提供 XML 标签,支持…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...
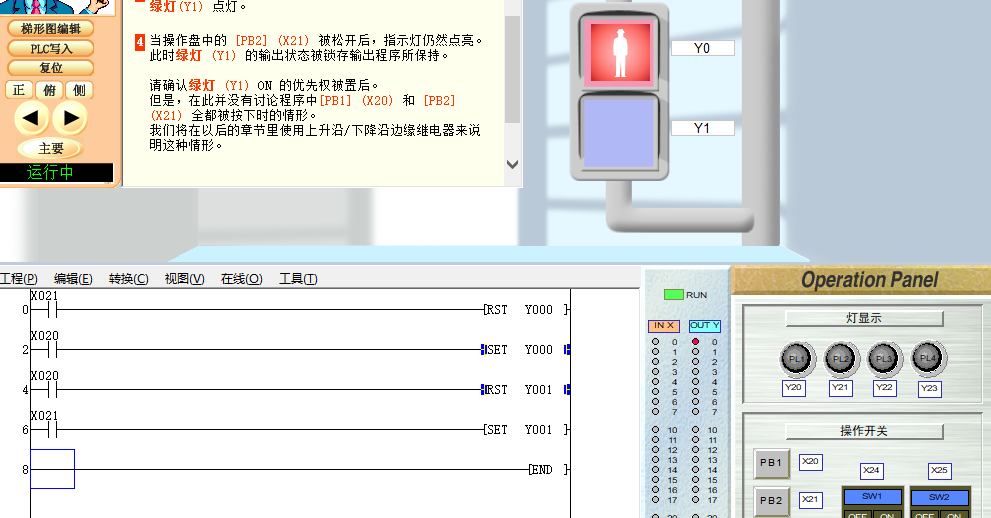
PLC入门【4】基本指令2(SET RST)
04 基本指令2 PLC编程第四课基本指令(2) 1、运用上接课所学的基本指令完成个简单的实例编程。 2、学习SET--置位指令 3、RST--复位指令 打开软件(FX-TRN-BEG-C),从 文件 - 主画面,“B: 让我们学习基本的”- “B-3.控制优先程序”。 点击“梯形图编辑”…...

详解ZYNQ中的 RC 和 EP
详解ZYNQ中的 RC 和 EP 一、ZYNQ FPGA 开发板基础( ZC706 ) 1. 核心特点 双核大脑 灵活积木: ZC706 集成了 ARM Cortex-A9 双核处理器(相当于电脑 CPU)和 FPGA 可编程逻辑单元(相当于可自定义的硬件积木…...

【电路笔记】-变压器电压调节
变压器电压调节 文章目录 变压器电压调节1、概述2、变压器电压调节3、变压器电压调节示例14、变压器电压调节示例25、变压器电压调节示例36、总结变压器电压调节是变压器输出端电压因连接负载电流的变化而从其空载值向上或向下变化的比率或百分比值。 1、概述 电压调节是衡量变…...
)
CSS中justify-content: space-between首尾贴边中间等距(两端元素紧贴左右边缘,中间元素等距均匀分布)
justify-content: space-between; 是 CSS Flexbox 布局中的一个属性值,主要作用是在弹性容器的主轴方向上均匀分布子元素,具有以下核心特性: 作用效果: 首尾贴边 第一个子元素紧贴容器起始端 最后一个子元素紧贴容器结束端 中…...
