【因果推断从入门到精通二】随机实验3

目录
检验无因果效应假说
硬币投掷的特殊性何在?
检验无因果效应假说
无因果效应假说认为,有些人存活,有些人死亡,但接受mAb114治疗而不是ZMapp与此无关。在174例接受mAb14治疗的患者中,113/174=64.9%存活了28天,在169例接受ZMapp治疗的病人中,有85/169=50.3%存活了28天。这是无因果效应假说为错误假说的确凿证据吗?这种差异可能是由偶然性——一系列运气不好的硬币投掷将人们分配给了mAb114或ZMapp——而不是由治疗引起的效应吗?
在PALM试验中,我们看到了几个我们知道是由硬币正面或反面掉落的偶然性造成的差异。硬币投掷显示,ZMapp组中有87名女性和82名男性,其中87/(87+82)=51.5%的比例为女性。硬币投掷将98名女性和76名男性纳入mAb114组,因此该组女性的比例为98/(98+76)=56.3%。这种差异,4.8%=56.3%-51.5%,是由偶然性,即硬币一次又一次下落的特殊方式造成的。存活率的差异,14.6%=64.9%一50.3%,是否也可能是由偶然性,而不是处理效应造成的呢?
显然,存活率的差异确实可能是由偶然性所致,前提是我们接受任38何逻辑上可能的东西现实中也可能。当然,没有人会这样做;如果你那
样想的话,你就连过马路也做不到了。许多逻辑上可能的事情都是不可
思议的。
在343例患者中,有113+85=198 例存活者,或比例为198/343一57.7%。在343例患者和198例存活者的总体中,如果没有处理效应,从逻辑上讲,一系列硬市投掷可能会选择174例患者和113例存活者施予mAb114,也可能选择169例患者和85例存活者施予ZMapp。事实上,这种情况可能以多种方式发生。实际上,有1.51×109个不同的343个正面和反面序列正是这样做的。尽管1.5×10乍一看似乎是一个令人印象深刻的大数字,但有7.4×101个348次硬币投掷序列,可以选择17%例患者施予mAb114。存活率的差异为14.6%=64.9%-50.3%,这可能是偶然造成的吗?这个问题显然比逻辑上的可能性更重要。
认为mAb114和ZMapp的效果没有差异的假说到底是什么呢?简单地说,我们经常谈到无因果效应假说,但我们的意思是,处理和对照情况的效果并没有什么不同。这一假说表明,343例患者中的每一例患者i,无论施予mAb114还是ZMapp,存活到28天的情况都是相同的。如同第一章所述,我们把mAb114写为T,把ZMapp写为C,无因果效应假说声称,对于每个i,都有rri=rc,i=1,2,…,343。这个假设通常被称为“费歇尔无因果效应假说”,因为它在他的随机实验理论中发挥了重要作用。关于硬币投掷,你必须相信些什么才能认同这个假说?如果这一假说是真的,14.6%=64.9%-50.3%的存活率差异会是一个常见的事件(比如在一枚公平硬币的两次投掷中得到两个正面),还是一个相当罕见的事件(比如投掷硬币七次得到七个正面)?
在一枚公平硬币的两次投掷中有两个正面的概率是(1/2)2=1/4,但在一枚公平硬币的七次投掷中有七个正面的概率是(1/2)'=0.0078。如果1000人投掷两次公平的硬币,我们预计250人会得到两个正面。如果1000人投掷七次公平的硬币,我们预计只有不到8人能得到七个正面。掷硬币七次得到七个正面,是怀疑硬币是否公平的理由,但掷硬币两次得到两个正面并不是怀疑硬币是否公平的理由。
PALM试验中的存活率类似于两次投掷中两个正面还是七次投掷中七个正面?如果在所有343例患者中,mAb114和ZMapp之间没有差异,那么14.6%的存活率差异是罕见还是常见事件呢?
在这一点上,有两个细节需要注意。事实上,mAb114以14.6%的优势击败了ZMapp。如果mAb114以大于14.6%的优势击败 ZMapp,那么我们的印象会更深刻。因此,我们真正在考虑的是差异等于或大于14.6%的概率,而不是差异正好等于14.6%的概率。此外,在试验之前,我们并不知道mAb114会是胜出者。如果ZMapp以14.6%的优势获胜,那么我们就将讨论ZMapp至少以14.6%获胜的可能性。我们来修正这两个细节,修正后的问题是:如果mAb114和ZMapp的效果没有差异,那么单是投掷硬币在存活方面产生明显差异的可能性有多大?是正的还是负的?与我们实际看到的差异一样大还是更大?事实证明,答案是0.0083。在PALM试验中,存活率的差异更接近于一枚硬币投掷七次得到七个正面,其概率为(1/2)7=0.0078,而不是两次投掷得到两个正面,其概率为(1/2)9=0.25。在mAb114导致的死亡率没有真正降低的情况下,要产生14.6%=64.9%一50.3%的存活差异,需要一个非常罕见的硬币投掷序列。
0.0083的概率是从哪里来的?它来自公平投掷硬币的表现。我们可以把任务交给计算机。无因果效应假说表明,343例患者中,无论给予mAb114还是ZMapp,都有113+85=198人存活,343-198=145人死亡,如果用一种药物替代另一种药物,没有人的存活率会发生改41变。这个假说可能是真的,也可能是假的,但上述内容就是假说之所言。在这个假说的总体中,我们可以告诉计算机投掷一枚公平硬币343次,通过投掷硬币将患者分配到mAb114组或ZMapp组。这将产生某个mAb114-ZMapp的存活率差异。这种存活率差异是由偶然性所致,因为在假说的总体中,没有人的存活取决于施予哪种药物。我们可以让计算机重复计算。如果计算机做了1000次这个任务,创建了1000个假的PALM试验,我们预计1000个中大约有8个会产生与我们看到的相同或更大的存活率差异,1000个中大约有992个会产生更小的存活率差异。我们看到的存活率差异14.6%=64.9%-50.3%,可能是由于偶然——这是一种逻辑上的可能性——但这是一种非常不可能的可能性。
简要概括一下,推理如下。我们的问题是,如果mAb114和ZMapp之间没有差异,那么观察到的14.6%=64.9%-50.3%的存活率差异是不是由一个患者被分配到mAb114,另一个患者被分配到ZMapp的不幸序列所致?我们发现这在逻辑上是可能的,但现实非常不可能:这样一个硬币投掷序列出现的概率是0.0083。为了维护42 mAb114和ZMapp对存活率的影响没有区别的观点,你一定要坚持说你是偶然观察到一个非常不可能的硬币投掷序列。
硬币投掷的特殊性何在?
随机实验根据一枚公平硬币新的投掷来分配处理或对照。在随机实
验中硬币投掷的哪些性质是重要的?哪些属性是次要的呢?
硬币正面朝上的概率是二分之一这一点并不重要。我们可以掷骰子,当1或2出现时,将一个人分配到处理组,当3、4、5或6出现时,将一个人分配到对照组。在这种情况下,进入处理组的概率是三分之一,而进人对照组的概率是三分之二,但这仍然是一个完全随机的实验。这类实验有时是在个体处理费用昂贵而对照条件不昂贵的情况下进行的。投掷硬币和掷骰子有一个重要的共同点:它们产生的是一种公平的彩票。这种彩票中奖的概率并不重要。关键之处在于,每个人都有相同的中奖机会。用硬币,中奖的概率是一半,但对每个人来说都是一半。前面所提到的那种掷骰子方式,中奖的概率是三分之一,但对每个人来说都是三分之一我们每个人都是独一无二的。不可能将独一无二的个人同时分配到处理组和对照组,从而使两组完全相同。华盛顿是独一无二的,如果他在一个组而不是另一个组,处理组和对照组就不可能完全相同。随机化并不能让不同的人变得相同;这是不可能的。由于是一种公平的彩票,随机化使得接受处理或对照与否,与使人们有所不同的一切因素都无关。在一切发生之前,我们经常说,这是那种能上大学的人,这是那种会进监狱的人,或者这是一个能成为好父亲的人。相比之下,在随机实验中,在实验发生之前,我们永远不能说,这是处理组的人的类型。因为这是一种公平的彩票,没有哪种类型的人最终会进入处理组。你可以根据自己的喜好虚构出不同类型的人,但一个人的类型永远无法预测他是否会受到处理,因为它永远无法预测投掷硬币的结果。
给乔治·华盛顿放血和体液说
18世纪的医生会发现放血对病人有害吗?我们来想想那个时代的医生们。他们有硬币。他们知道怎么投掷它们。他们可以衡量结果,区分死者和生者。他们甚至对概率有基本的了解。他们缺少的是什么呢?也许,正如之前提到的,他们缺少的是杜威所称的那种实验的思维习惯。
如果18世纪发现病人因放血而受到伤害,医生们可能会对建立在体液理论基础上的医学知识结构提出质疑。随机试验中一项处理的成败可能会刺激疾病生物学的基础研究;这反过来可能会产生更好的治疗方法,以便在进一步的试验中进行评估
-就像今天一样。
print('要天天开心啊')相关文章:

【因果推断从入门到精通二】随机实验3
目录 检验无因果效应假说 硬币投掷的特殊性何在? 检验无因果效应假说 无因果效应假说认为,有些人存活,有些人死亡,但接受mAb114治疗而不是ZMapp与此无关。在174例接受mAb14治疗的患者中,113/17464.9%存活了28天&…...
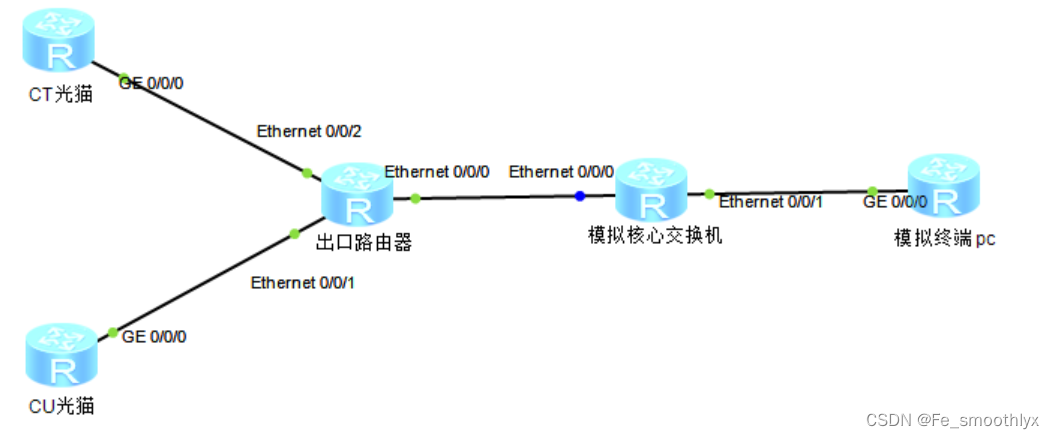
真实案例分享,终端pc直接telnet不到出口路由器。
1、背景信息 我终端pc的网卡地址获取的网关是在核心交换机上,在核心交换机上telnet出口路由器可以实现。 所有终端网段都不能telnet出口路由器,客户希望能用最小的影响方式进行解决。 2、现有配置信息 终端的无线和有线分别在两个网段中,…...

YOLOv8_seg的训练、验证、预测及导出[实例分割实践篇]
实例分割数据集链接,还是和目标检测篇一样,从coco2017val数据集中挑出来person和surfboard两类:链接:百度网盘 请输入提取码 提取码:3xmm 1.实例分割数据划分及配置 1.1实例分割数据划分 从上面得到的数据还不能够直接训练,需要按照一定的比例划分训练集和验证集,并按…...

Linux基础(四):Linux系统文件类型与文件权限
各位看官,好久不见,在正式介绍Linux的基本命令之前,我们首先了解一下,关于文件的知识。 目录 一、文件类型 二、文件权限 2.1 文件访问者的分类 2.2 文件权限 2.2.1 文件的基本权限 2.2.2 文件权限值的表示方法 三、修改文…...

本是梦中人,常作花下客。心中自往来,知我有几个。
我们总是喜欢拿“顺其自然”来敷衍人生道路上的荆棘坎坷,却很少承认,真正的顺其自然, 其实是竭尽所能之后的不强求, 而非两手一摊的不作为。 一花凋零荒芜不了整个春天, 一次挫折也荒废不了整个人生。 多年后&#x…...

创新指南|利用电商产品视频进行渠道营销的最佳策略,不断提升销售额
无论企业的利基市场如何,电商产品视频都已被证明是非常可靠的资产,可以让目标受众了解您所提供的产品——关键功能、展示重要的差异化优势甚至改变大多数营销活动的游戏规则。阅读本文,全面了解电商产品视频如何融入营销推广,以最…...
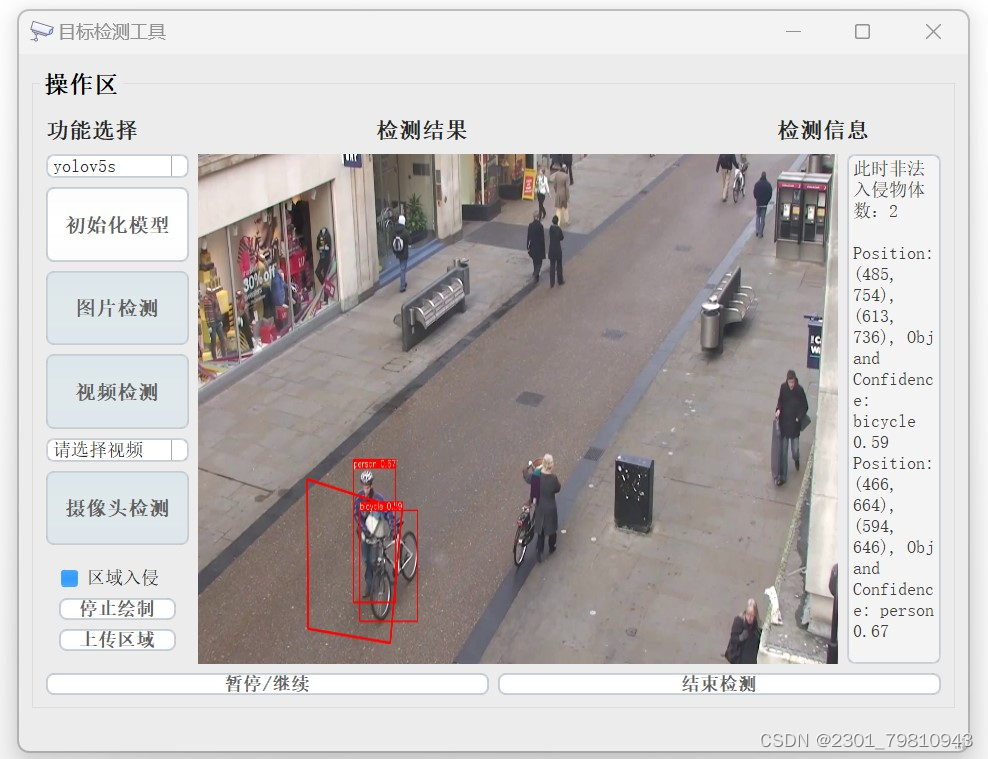
深度学习之基于YoloV5入侵检测系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 一、项目背景 随着信息技术的飞速发展,网络安全问题日益凸显。入侵检测系统(IDS࿰…...
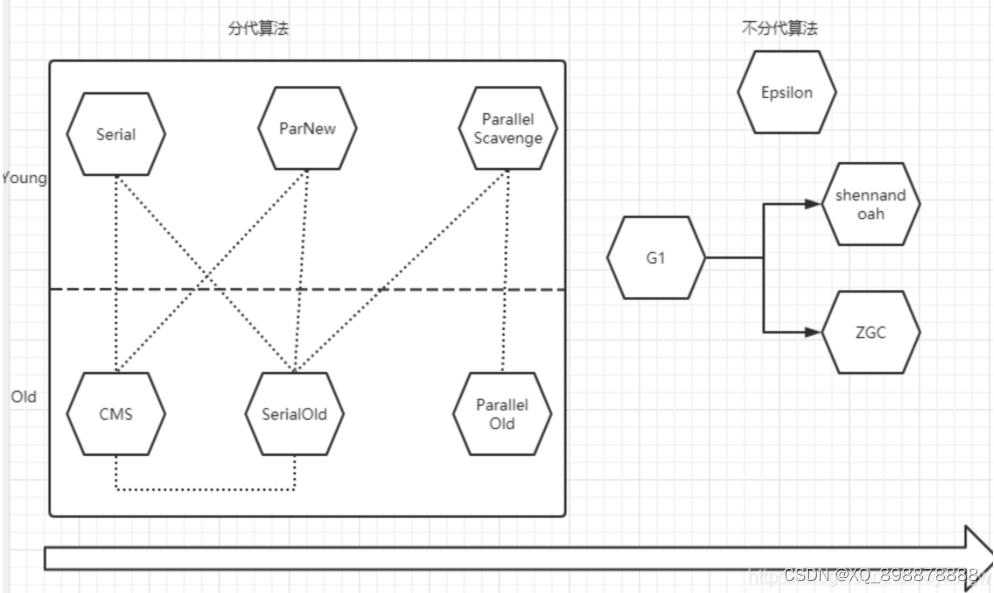
【01】全面理解JVM虚拟机
一、前言 学习JVM是进行JVM调优的基础。写的代码部署到线上它会如何运行?要配多少内存?线上环境出问题了,服务崩溃了,应该怎么快速定位?这些问题都与JVM有着一定的关系。好的程序员都应该尽自己的能力把JVM每个底层逻…...
CentOS7离线安装Nginx
目录 1. 安装gcc2. 安装g3. 安装openssl4. 安装pcre5. 安装zlib6. 安装Nginx7. 启动nginx8. 开放80端口9. 访问测试10. 设置开机自启 Nginx离线安装需要依赖gcc、g环境,安装前要先检查linux系统中是否自带gcc和g,如果没有就需要先进行安装。 然后再安装o…...

面试字节大模型算法实习岗,感觉有点崩溃。。。
节前,我们组织了一场算法岗技术&面试讨论会,邀请了一些互联网大厂朋友、今年参加社招和校招面试的同学。 针对大模型技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备面试攻略、面试常考点等热门话题进行了深入的讨论。 总结链接…...
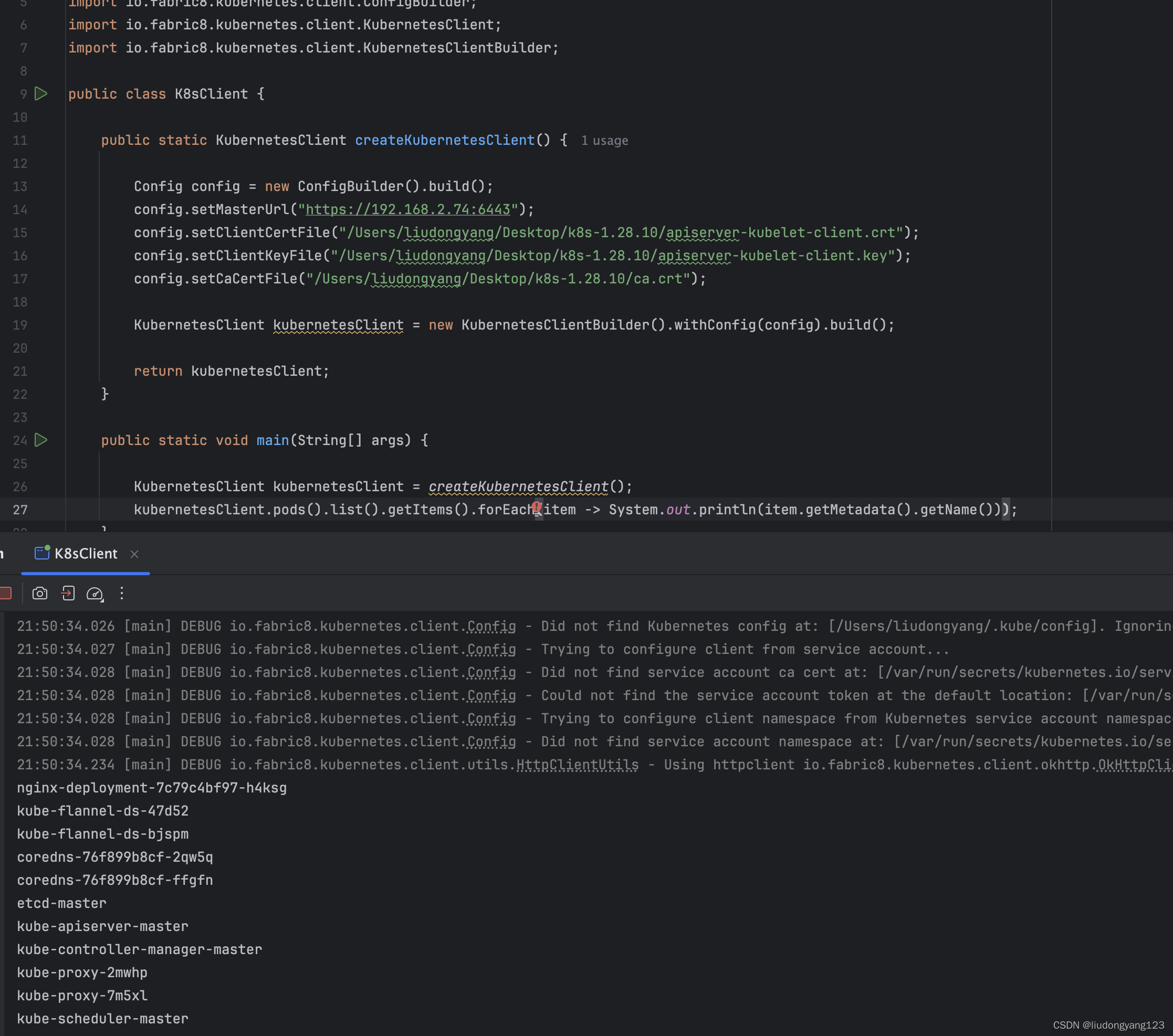
k8s 1.24.x之后如果rest 访问apiserver
1.由于 在 1.24 (还是 1.20 不清楚了)之后,下面这两个apiserver的配置已经被弃用 了,简单的说就是想不安全的访问k8s是不可能了,所以只能走安全的访问方式也就是 https://xx:6443了,所以需要证书。 - --ins…...

深度解析:用 Python 爬虫逆向破解 solscan 的请求头加密参数 Sol-Aut
大家好!我是爱摸鱼的小鸿,关注我,收看每期的编程干货。 逆向是爬虫工程师进阶必备技能,当我们遇到一个问题时可能会有多种解决途径,而如何做出最高效的抉择又需要经验的积累。本期文章将以实战的方式,带你详细地逆向分析 solscan 网站请求头加密字段 Sol-Aut 的构造逻辑,…...

Flutter 中的 InputDecorator 小部件:全面指南
Flutter 中的 InputDecorator 小部件:全面指南 在Flutter中,InputDecorator是一个用于装饰输入字段的组件,它为TextField和TextFormField提供了一个统一的外观和布局。InputDecorator可以让您自定义输入框的标签、填充、边框、图标、光标、错…...

useTransition:开启React并发模式
写在前面:并发 并发模式(Concurrent Mode)1的一个关键特性是渲染可中断。 React 18 之前,更新内容渲染的方式是通过一个单一的且不可中断的同步事务进行处理。同步渲染意味着,一旦开始渲染就无法中断,直到…...

Android 12系统源码_多窗口模式(二)系统实现分屏的功能原理
前言 上一篇我们具体分析了系统处于多窗口模式下,Android应用和多窗口模式相关方法的调用顺序,对于应用如何适配多窗口模式有了一个初步的认识,本篇文章我们将会结合Android12系统源码,具体来梳理一下系统是如何触发多窗口分屏模…...

字符函数:分类函数与转换函数
字符函数 一.字符分类函数二.字符转换函数 在编程的过程中,我们经常要处理字符和字符串,为了方便操作字符和字符串,C语⾔标准库中提供了一系列库函数,接下来我们就学习⼀下这些函数。 一.字符分类函数 C语言中有⼀系列的函数是专门…...

SpringBoot 集成Mybatis
SpringBoot集成第三方技术,一般都分为导坐标,改配置,写代码三个步骤。 集成Mybatis也类似,新建一个SpringBoot项目。修改:pom.xml文件。 一、导入坐标 <!--druid--> <dependency><groupId>com.al…...

C语言-atoi()库函数的模拟实现
文章目录 前言一、atoi()库函数的介绍及使用1.1 atoi()库函数介绍1.2 atoi()库函数使用 二、atoi()库函数的模拟实现2.1 函数设计2.2 函数实现思路2.3 具体实现2.4 测试 总结 前言 本篇文章介绍c语言中库函数atoi()的使用,以及模拟实现库函数。 一、atoi()库函数的…...

定时监测服务器磁盘是否超过阈值,超过就删除docker 镜像
达到指定百分比 删除镜像脚本 df -h 查找到 内存占用信息 ,得到的 文件系统名称是 overlay的,Use% 达到70就进行删除docker 镜像 #!/bin/bash# 设置磁盘使用阈值 THRESHOLD70# 获取 overlay 文件系统的磁盘使用百分比 DISK_USAGES$(df -h | grep overl…...

UDP聊天室
服务器端 #include <myhead.h>#define SER_IP "192.168.124.38" #define SER_PORT 8888 #define RBUFSIZE 128 #define WBUFSIZE 128typedef struct node{char usrName[20];struct sockaddr_in cli_sockaddr;struct node* next; }node, *node_p;node_p create…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
