当前位置： 首页 > news >正文

机器学习--数学部分笔记

news 2026/2/9 10:32:11

前言

因为周三要考试,所以数学部分写一下笔记

正文

随机事件和随机实验

条件概率

• 在已知事件 𝐵 发生的条件下，事件𝐴发生的概率称为事件 𝐴 的条件概率，记为𝑃(𝐴|𝐵)

全概率公式

贝叶斯公式

相关文章：

机器学习--数学部分笔记

前言 因为周三要考试,所以数学部分写一下笔记 正文 随机事件和随机实验 条件概率 • 在已知事件 𝐵 发生的条件下，事件𝐴发生的概率称为事件 𝐴 的条件概率，记为𝑃(𝐴|𝐵) 全概率…...

编程日记 2024/5/25 14:29:33

基于springboot的在线宠物用品交易网站源码数据库

基于springboot的在线宠物用品交易网站源码数据库 随着信息技术在管理上越来越深入而广泛的应用，管理信息系统的实施在技术上已逐步成熟。本文介绍了在线宠物用品交易网站的开发全过程。通过分析在线宠物用品交易网站管理的不足，创建了一个计算机管理在…...

编程日记 2024/5/25 14:26:29

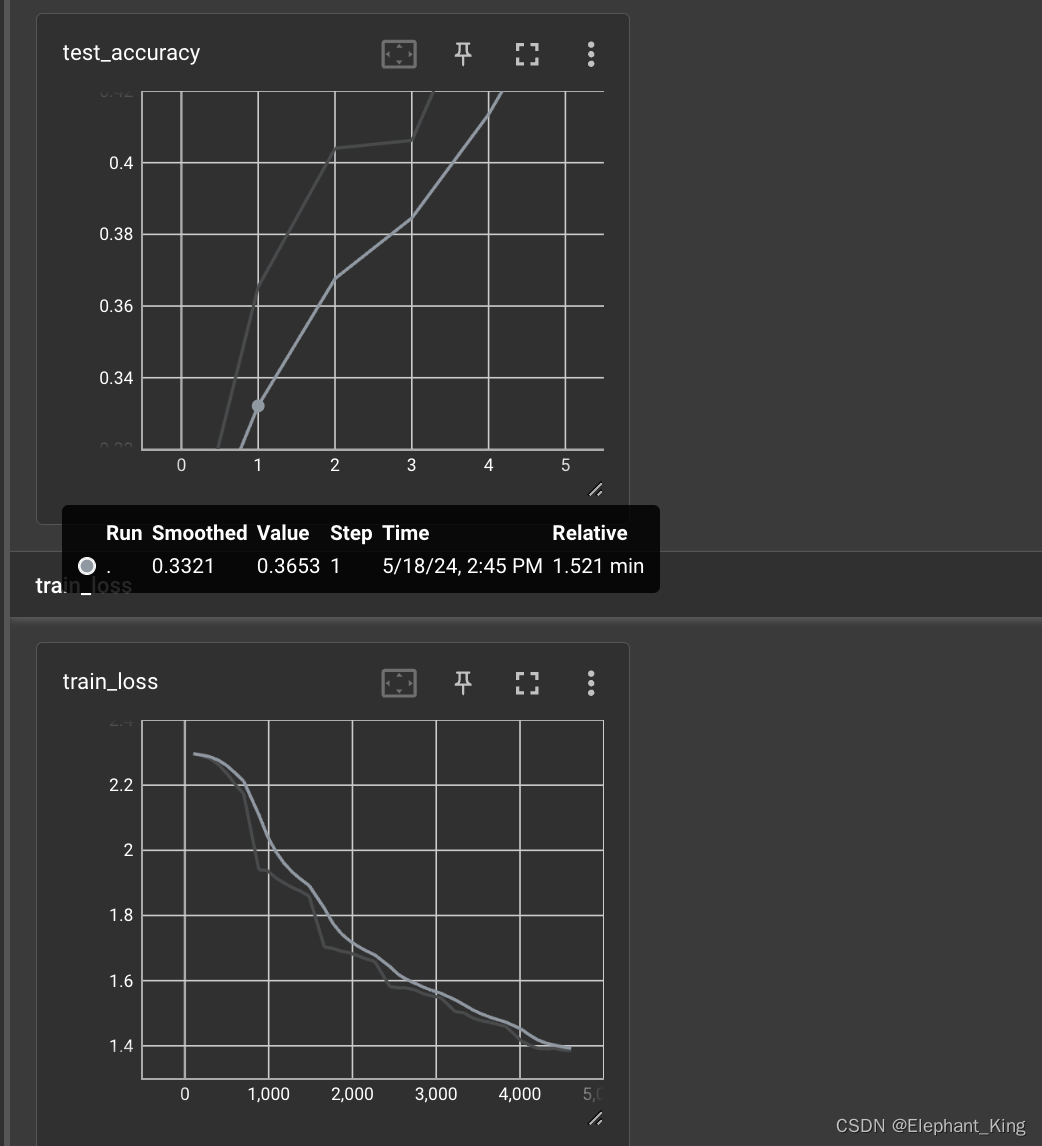
【Pytorch】13.搭建完整的CIFAR10模型

项目源码 已上传至githubCIFAR10Model，如果有帮助可以点个star 简介 在前文【Pytorch】10.CIFAR10模型搭建我们学习了用Module来模拟搭建CIFAR10的训练流程 本节将会加入损失函数，梯度下降，TensorBoard来完整搭建一个训练的模型 基本步骤 搭建…...

编程日记 2024/5/25 14:25:28

护目镜佩戴自动识别预警摄像机

护目镜佩戴自动识别预警摄像机是一种智能监测设备，专门用于佩戴护目镜的工人进行作业时，能够自动识别有潜在风险的场景，并及时发出预警信号。该摄像机配备人脸识别和智能预警系统，可以检测危险情况并为工人提供实时安全保护&#…...

编程日记 2024/5/25 14:22:25

keep-alive的使用

Vue中的<keep-alive>组件是前端开发中的一个宝藏功能&#xff0c;它如同时光胶囊般保留组件的状态&#xff0c;让组件在切换时仿佛按下暂停键&#xff0c;再次回来时还能继续播放&#xff0c;极大地优化了用户体验和性能。&#x1f680;✨ 作用 状态保留&#xff1a;当包…...

编程日记 2024/5/25 14:21:24

【Linux】中的常见的重要指令（中）

目录 一、man指令 二、cp指令 三、cat指令 四、mv指令 五、more指令 六、less指令 七、head指令 八、tail指令 一、man指令 Linux的命令有很多参数&#xff0c;我们不可能全记住&#xff0c;我们可以通过查看联机手册获取帮助。访问Linux手册页的命令是 man 语法: m…...

编程日记 2024/5/25 14:20:23

营收净利双降、股东减持，大降价也救不了良品铺子

号称“高端零食第一股”的良品铺子(603719.SH)&#xff0c;正遭遇部分股东的“用脚投票”。 5月17日晚间&#xff0c;良品铺子连发两份减持公告&#xff0c;其控股股东宁波汉意创业投资合伙企业、持股5%以上股东达永有限公司&#xff0c;两者均计划减持。 其中&#xff0c;宁…...

编程日记 2024/5/25 14:19:21

【设计模式】设计模式的分类

通常设计模式的分类有创建型、行为型和结构型。 创建型 常用的有&#xff1a;单例模式、工厂模式&#xff08;工厂方法和抽象工厂&#xff09;、建造者模式。 不常用的有&#xff1a;原型模式。 创建型模式涉及到将对象实例化&#xff0c;这类模式都提供一个方法&#xff0c;将…...

编程日记 2024/5/25 14:18:20

TCP/UDP的连接机制

TCP/UDP的连接机制 TCP的连接机制 TCP&#xff08;Transmission Control Protocol&#xff09;是一种面向连接的协议&#xff0c;提供可靠的、按顺序的数据传输服务。TCP的连接机制包括连接建立、数据传输和连接终止。 1. 连接建立&#xff08;三次握手&#xff09; TCP通过…...

编程日记 2024/5/25 14:17:18

供应链金融模式学习资料

目录 产生背景 供应链金融的诞生 供应链金额的六大特征...

编程日记 2024/5/25 14:16:18

代码随想录-算法训练营day50【动态规划12：最佳买卖股票时机含冷冻期、买卖股票的最佳时机含手续费、股票问题总结】

代码随想录-035期-算法训练营【博客笔记汇总表】-CSDN博客 第九章 动态规划part12● 309.最佳买卖股票时机含冷冻期 ● 714.买卖股票的最佳时机含手续费 ●总结309.最佳买卖股票时机含冷冻期 本题加了一个冷冻期，状态就多了，有点难度，大家要把各个状态分清，思路才能清晰…...

编程日记 2024/5/25 14:15:17

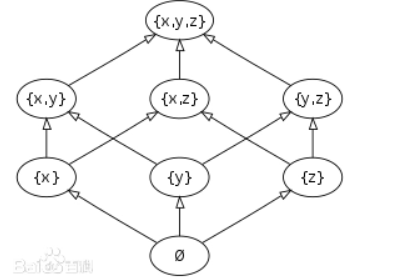
Dilworth 定理

这是一个关于偏序集的定理&#xff0c;事实上它也可以扩展到图论&#xff0c;dp等中&#xff0c;是一个很有意思的东西 偏序集 偏序集是由集合 S S S以及其上的一个偏序关系 R R R定义的&#xff0c;记为 ( S , R ) (S,R) (S,R) 偏序关系&#xff1a; 对于一个二元关系 R ⊂…...

编程日记 2024/5/25 14:14:16

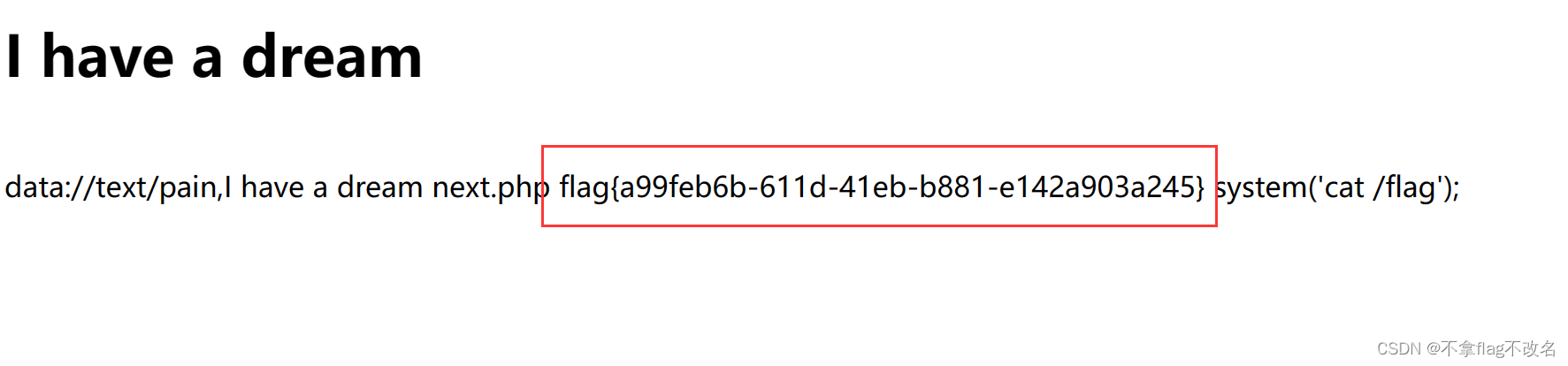
BUUCTF---web---[BJDCTF2020]ZJCTF，不过如此

1、点开连接&#xff0c;页面出现了提示 传入一个参数text&#xff0c;里面的内容要包括I have a dream。 构造&#xff1a;?/textI have a dream。发现页面没有显示。这里推测可能得使用伪协议 在文件包含那一行&#xff0c;我们看到了next.php的提示&#xff0c;我们尝试读取…...

编程日记 2024/5/25 14:13:14

力扣刷题---2206. 将数组划分成相等数对【简单】

题目描述&#x1f357; 给你一个整数数组 nums &#xff0c;它包含 2 * n 个整数。 你需要将 nums 划分成 n 个数对&#xff0c;满足&#xff1a; 每个元素 只属于一个 数对。 同一数对中的元素 相等 。 如果可以将 nums 划分成 n 个数对&#xff0c;请你返回 true &#xf…...

编程日记 2024/5/25 14:12:13

2461. 长度为 K 子数组中的最大和（c++）

给你一个整数数组 nums 和一个整数 k 。请你从 nums 中满足下述条件的全部子数组中找出最大子数组和&#xff1a; 子数组的长度是 k&#xff0c;且子数组中的所有元素 各不相同 。 返回满足题面要求的最大子数组和。如果不存在子数组满足这些条件&#xff0c;返回 0 。 子数…...

编程日记 2024/5/25 14:10:11

range for

1. 基于范围的for循环语法 C11标准引入了基于范围的for循环特性&#xff0c;该特性隐藏了迭代器 的初始化和更新过程&#xff0c;让程序员只需要关心遍历对象本身&#xff0c;其语法也 比传统for循环简洁很多&#xff1a; for ( range_declaration : range_expression ) {loo…...

编程日记 2024/5/25 14:08:08

leetcode230 二叉搜索树中第K小的元素

题目 给定一个二叉搜索树的根节点 root &#xff0c;和一个整数 k &#xff0c;请你设计一个算法查找其中第 k 个最小元素&#xff08;从 1 开始计数&#xff09;。 示例 输入&#xff1a;root [5,3,6,2,4,null,null,1], k 3 输出&#xff1a;3 解析 这道题应该是能做出…...

编程日记 2024/5/25 14:07:07

.Net Core学习笔记 框架特性（注入、配置）

注&#xff1a;直接学习的.Net Core 6&#xff0c;此版本有没有startup.cs相关的内容 项目Program.cs文件中 是定义项目加载 启动的地方 //通过builder对项目进行配置、服务的加载 var builder WebApplication.CreateBuilder(args); builder.Services.AddControllers();//将…...

编程日记 2024/5/25 14:06:05

利用AI技术做电商网赚，这些百万级赛道流量，你还不知道？！

大家好&#xff0c;我是向阳 AI技术的飞速扩展已经势不可挡&#xff0c;不管你承不承认&#xff0c;AI 已经毫无争议的在互联网中占有一席之地了 无论你是做内容产业的&#xff0c;还是做电商的&#xff0c;你现在都躲不开 AI。 现在互联网行业的竞争就是这么残酷 互联网行业…...

编程日记 2024/5/25 14:05:04

leetcode-560 和为k的数组

一、题目描述 给你一个整数数组 nums 和一个整数 k &#xff0c;请你统计并返回 该数组中和为 k 的子数组的个数 。 子数组是数组中元素的连续非空序列。 注意&#xff1a;nums中的元素可为负数 输入&#xff1a;nums [1,1,1], k 2 输出&#xff1a;2输入&#xff1a;num…...

编程日记 2024/5/25 14:02:01

基于服务器使用 apt 安装、配置 Nginx

&#x1f9fe; 一、查看可安装的 Nginx 版本 首先&#xff0c;你可以运行以下命令查看可用版本&#xff1a; apt-cache madison nginx-core输出示例&#xff1a; nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

编程新知 2026/1/9 12:53:59

ffmpeg（四）：滤镜命令

FFmpeg 的滤镜命令是用于音视频处理中的强大工具&#xff0c;可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下&#xff1a; ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜&#xff1a; ffmpeg…...

编程新知 2026/2/4 23:47:47

Qt Http Server模块功能及架构

Qt Http Server 是 Qt 6.0 中引入的一个新模块&#xff0c;它提供了一个轻量级的 HTTP 服务器实现&#xff0c;主要用于构建基于 HTTP 的应用程序和服务。 功能介绍&#xff1a; 主要功能 HTTP服务器功能&#xff1a; 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

编程新知 2025/10/17 21:16:57

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用

1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

编程新知 2025/10/3 17:30:30

【Android】Android 开发 ADB 常用指令

查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

编程新知 2025/11/18 18:31:30

python爬虫——气象数据爬取

一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用&#xff1a; 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests&#xff1a;发送 …...

编程新知 2025/12/16 7:53:39

第八部分：阶段项目 6：构建 React 前端应用

现在&#xff0c;是时候将你学到的 React 基础知识付诸实践&#xff0c;构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段&#xff0c;你可以先使用模拟数据&#xff0c;或者如果你的后端 API&#xff08;阶段项目 5&#xff09;已经搭建好&#xff0c;可以直接连…...

编程新知 2025/9/21 1:58:01

云安全与网络安全：核心区别与协同作用解析

在数字化转型的浪潮中&#xff0c;云安全与网络安全作为信息安全的两大支柱&#xff0c;常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异&#xff0c;并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全&#xff1a;聚焦于保…...

编程新知 2026/2/8 1:53:29

ui框架-文件列表展示

ui框架-文件列表展示 介绍 UI框架的文件列表展示组件&#xff0c;可以展示文件夹&#xff0c;支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项&#xff0c;适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

编程新知 2026/2/4 17:34:02

React从基础入门到高级实战：React 实战项目 - 项目五：微前端与模块化架构

React 实战项目&#xff1a;微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇&#xff01;在前 29 篇文章中&#xff0c;我们从 React 的基础概念逐步深入到高级技巧&#xff0c;涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

编程新知 2025/10/18 20:50:06