HarmonyOS 鸿蒙应用开发 - 创建自定义组件
开发者定义的称为自定义组件。在进行 UI 界面开发时,通常不是简单的将系统组件进行组合使用,而是需要考虑代码可复用性、业务逻辑与UI分离,后续版本演进等因素。因此,将UI和部分业务逻辑封装成自定义组件是不可或缺的能力。
1、创建自定义组件
1、组件必须使用 @Component 修饰 ;
2、@Entry 修饰 表示应用程序入口
3、build 方法里面必须有一个根容器 :如 Row 、Column 等
4、在自定组件中,任务成员都是私有(类似 java的 private)
5、@State状态机制,自动更新build方法里的内容
6、this 可以获取成员变量
列如:
//自定义组件
@Component
struct CountButton {//在自定组件中,任务成员都是私有(类似 java的 private)tip: String = "计数按钮"//@State状态机制,自动更新build方法里的内容@State count: number = 0build() {Column() { //根组件Text(this.tip + '').margin({ top: 10 }).fontColor(Color.Black).fontWeight(FontWeight.Bold).fontSize(20)Row() {Text(this.count + '').fontColor(Color.Red).fontSize(20)Button('点击计数').width(120).margin({left:10}).onClick(()=>{this.count+=1;})}.margin({top:14})}.width(200).height(100).backgroundColor('#89CFF0').borderRadius(12)}
}
2、使用自定义组件
@Entry
@Component
struct CommonText{build(){Column(){Text("使用自定义组件").fontSize(30).margin({top:20,bottom:20})CountButton() //使用自定义组件CountButton().margin({top:20})}.height('100%').width('100%').alignItems(HorizontalAlign.Center)//水平居中}
}3、效果图
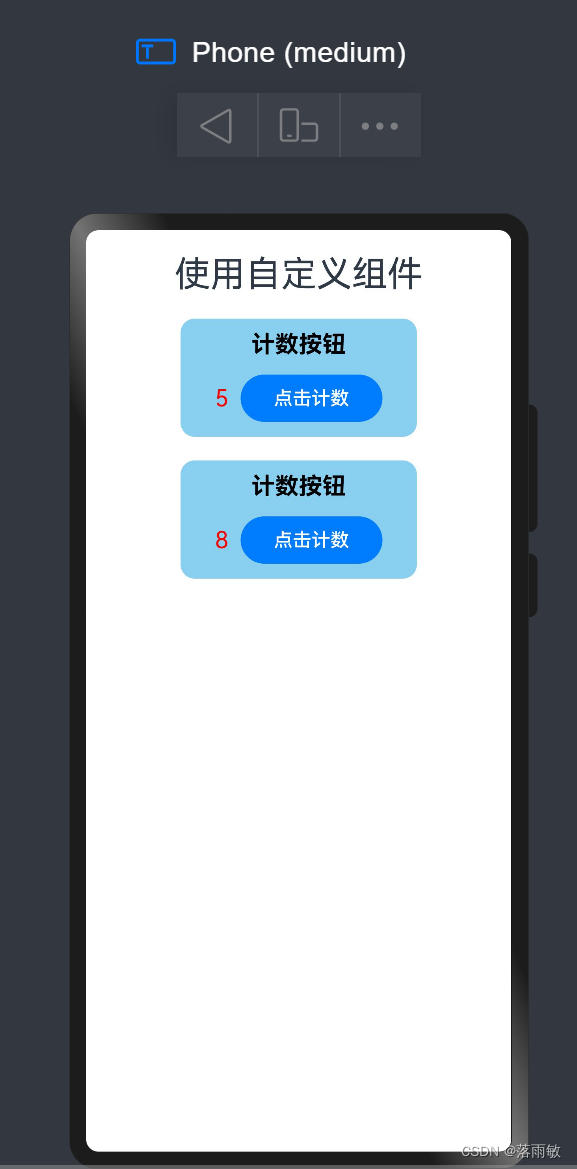
相关文章:

HarmonyOS 鸿蒙应用开发 - 创建自定义组件
开发者定义的称为自定义组件。在进行 UI 界面开发时,通常不是简单的将系统组件进行组合使用,而是需要考虑代码可复用性、业务逻辑与UI分离,后续版本演进等因素。因此,将UI和部分业务逻辑封装成自定义组件是不可或缺的能力。 1、创…...
【Vue3】封装axios请求(cli和vite)
原文作者:我辈李想 版权声明:文章原创,转载时请务必加上原文超链接、作者信息和本声明。 Vue 【Vue3】env环境变量的配置和使用(区分cli和vite) 文章目录 Vue前言一、常见用法二、vue3cli封装接口1..env配置2..dev(开…...

Java8 Optional常用方法使用场景
前言: Optional 是 Java 8 的新特性,专治空指针异常(NullPointerException, 简称 NPE)问题,它是一个容器类,里面只存储一个元素(这点不同于 Conllection)。 为方便用户通过 Lambda 表…...

isscc2024 short course4 In-memory Computing Architectures
新兴的ML加速器方法:内存计算架构 1. 概述 内存计算(In-memory Computing)架构是一种新兴的机器学习加速器方法,通过将计算能力集成到存储器中,以减少数据移动的延迟和能耗,从而提高计算效率和性能。这种方…...

ubuntu 安装 kvm 启动虚拟机
1. 基础环境设置 #更新环境 apt update apt upgrade#配置网卡 cat >/etc/netplan/br.yml<<EOF network:ethernets:eth2: {}bridges:br0:interfaces:- eth2addresses:- 192.192.1.213/24gateway4: 192.192.1.1nameservers:addresses:- 8.8.8.8- 8.8.4.4 EOF #安装组件…...

[OpenGL] opengl切线空间
目录 一 引入 二 TBN矩阵 三 代码实现 3.1手工计算切线和副切线 3.2 像素着色器 3.3 切线空间的两种使用方法 3.4 渲染效果 四 复杂的物体 本章节源码点击此处 继上篇法线贴图 来熟悉切线空间是再好不过的。对于法线贴图来说,我们知道它就是一个2D的颜色纹理,根据rgb…...

SpringCloud微服务03-微服务保护-分布式事务-MQ基础-MQ高级
一、微服务保护 1.雪崩问题 如何做好后备方案就是后续: 2.雪崩解决方案 某一个服务的线程是固定的,出现故障线程占满后,就不会让取调用这个服务,对其他服务就没有影响。 3.Sentinel ①初识Sentinel 配置过程:day05-服…...

住宅IP?
住宅IP是由主要运营商(如电信、移动、联通等)为用户开通的宽带业务所分配的IP地址。这些IP地址是真实的、具有实际位置的IP,与普通用户的设备IP和宽带网络IP一致。它们不是连续的,而是散点分布,这使得它们在使用时更加…...

SpringBoot实现邮箱验证码
自行创建一个SpringBoot项目 导入SpringBoot所需要的邮箱验证码的包 <!--邮件发送--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId><version>2.6.1</version>…...

GPT提示词技巧,使用教程,国内版官网直达,非套壳
GPT提示词技巧,使用教程,国内版官网直达,非套壳 主站点:https://chatgpt-plus.top(江苏福建地区打不开,需要魔法) 店铺地址:https://buy.chatgpt-plus.top/ 选择plus账号进入&…...
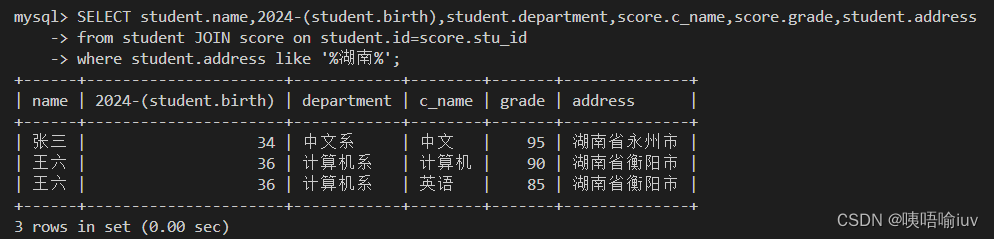
MySQL多表关联查询习题
一、素材 -- Active: 1714203732007127.0.0.13306db_stu -- 1.创建student和score表 CREATE TABLE student ( id INT(10) NOT NULL UNIQUE PRIMARY KEY , name VARCHAR(20) NOT NULL , sex VARCHAR(4) , birth YEAR, department VARCHAR(20) , address VARCHAR(50) ); -- 创建…...
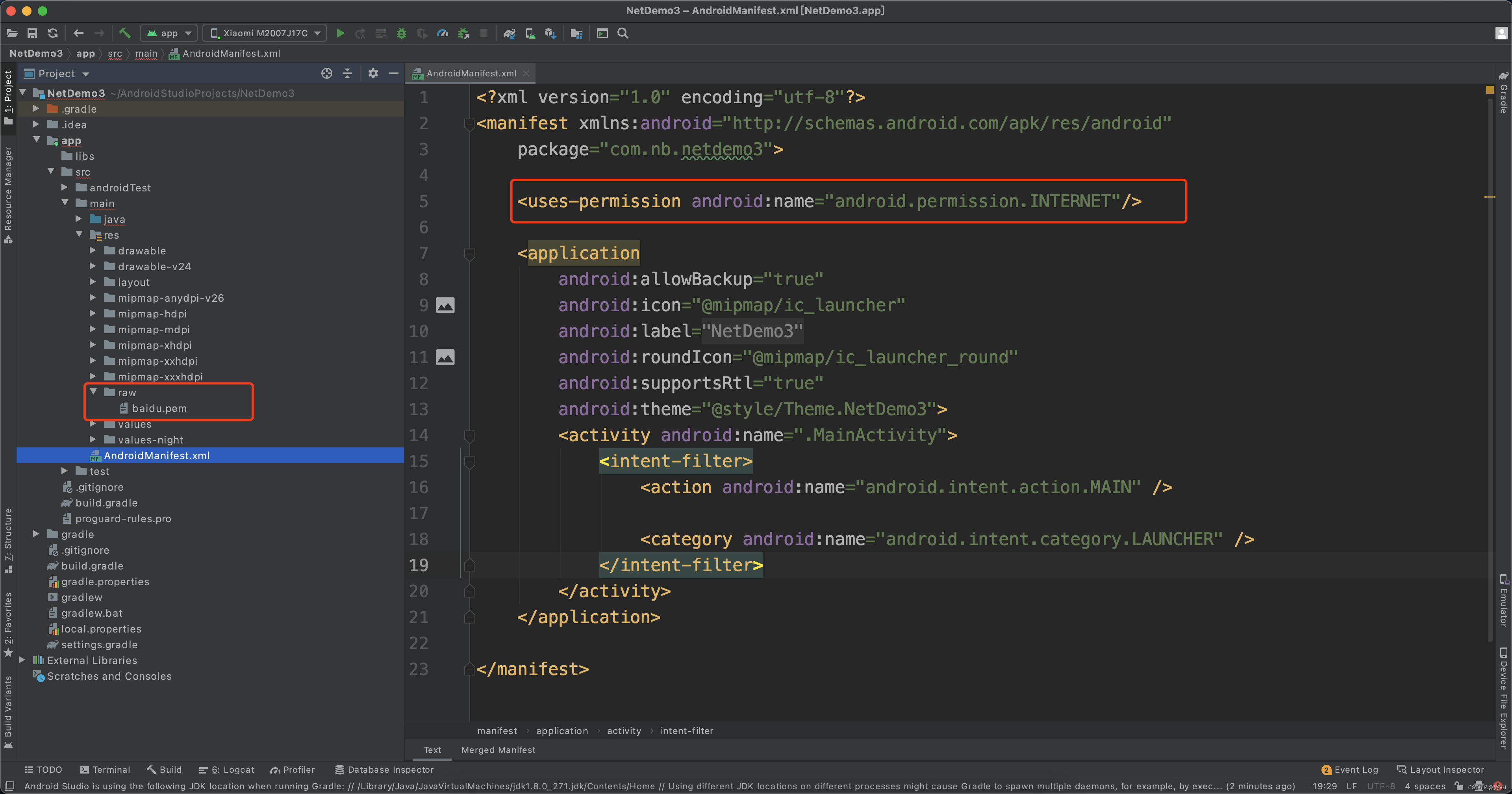
Android正向开发实现客户端证书认证
前言 如果第三方模块被混淆,那hook方式均不能生效。这时就需要根据系统包去定位校验的函数,因此需要对安卓开发者是如何实现客户端证书校验的有一定了解,接下来就介绍这部分内容。 开发者实现客户端证书校验的本质是:证书/密钥 + 代码。 在形式上有:证书校验、公钥校验和…...

【Kubernetes】Pod无法访问Service域名问题排查
背景 部署过多套k8s集群,发现在其中一套k8s环境中,在Pod内无法访问Service Name,访问了很多次,偶尔又能通,使用Service的IP能正常访问,域名解析的问题基本确定与CoreDNS有关系,于是开始了一系列…...

【JAVA基础之网络编程】UDP和TCP协议以及三次握手和四次挥手的过程
🔥作者主页:小林同学的学习笔录 🔥mysql专栏:小林同学的专栏 目录 1. 网络编程 1.1 概述 1.2 网络编程的三要素 1.2.1 IP地址 1.2.2 InetAddress 1.2.3 端口和协议 1.3 UDP协议 1.3.1 UDP发送数据 1.3.2 UDP接收数据 1.4…...

基于python+Django大数据的电影市场预测分析系统设计与实现
博主介绍: 大家好,本人精通Java、Python、C#、C、C编程语言,同时也熟练掌握微信小程序、Php和Android等技术,能够为大家提供全方位的技术支持和交流。 我有丰富的成品Java、Python、C#毕设项目经验,能够为学生提供各类…...

消息传递与集成:使用Springboot进行异步通信
消息传递与集成:使用Spring Boot进行异步通信 在现代的分布式系统中,异步通信已经成为了一种常见的设计模式。通过使用消息队列和事件驱动架构,我们可以实现系统之间的解耦,提高系统的可扩展性和可靠性。本文将介绍如何使用Sprin…...
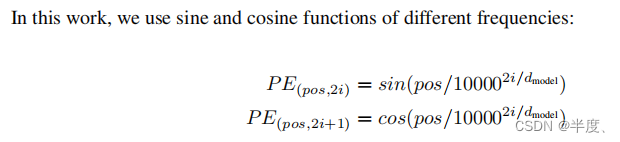
【论文速读】Transformer:Attention Is All You Need
Transformer:Attention Is All You Need 摘要模型架构注意力模型Scaled Dot-ProductMulti-Head Attention Position-wise Feed-Forward NetworksEmbeddings and SoftmaxPositional Encoding 摘要 我们提出了一种新的简单的网络架构,Transformer…...

小短片创作-组装场景(一)
1、项目基础设置 通过第三人称模板,创建1个项目 1.自动曝光:关闭,因为要做专业的小短片,曝光需要手动控制。 2.扩展自动曝光中的默认亮度范围:启用 3.全局光照系统:选择屏幕空间光照(SSGI&am…...
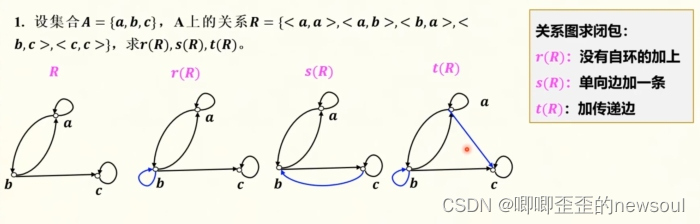
二元关系表示
一、二元关系的定义和表示 什么是二元关系?对集合A和B,A\timesB的任意子集R为A到B的一个二元关系。当AB时,A\timesA的任一子集R称为A上的一个二元关系。在不引起误解的情况下,二元关系可简称关系。 若|A|m,|B|n,则A到…...
)
Android Audio基础——AudioFlinger音频流管理(八)
从前面 AudioTrack、PlaybackThread、输出流设备三者的关系中,我们看到 AudioTrack 把音频流数据送入到对应的 PlaybackThread 中,那么应用进程是如何控制音频流的开始播放 start()、停止播放 stop()、暂停播放 pause()。这一章节我们就来继续分析。 一、音频流管理 应用进程…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
