leetcode力扣 2024. 考试的最大困扰度
一位老师正在出一场由 n 道判断题构成的考试,每道题的答案为 true (用 ‘T’ 表示)或者 false (用 ‘F’ 表示)。老师想增加学生对自己做出答案的不确定性,方法是最大化有连续相同结果的题数。(也就是连续出现 true 或者连续出现 false)。
给你一个字符串 answerKey,其中 answerKey[i] 是第 i 个问题的正确结果。除此以外,还给你一个整数 k,表示你能进行以下操作的最多次数:
每次操作中,将问题的正确答案改为 ‘T’ 或者 ‘F’(也就是将 answerKey[i] 改为 ‘T’ 或者 ‘F’)。请你返回在不超过 k 次操作的情况下,最大连续 ‘T’ 或者 ‘F’ 的数目。
示例 1:
输入:answerKey = “TTFF”, k = 2
输出:4
解释:我们可以将两个 ‘F’ 都变为 ‘T’,得到 answerKey = “TTTT”。
总共有四个连续的 ‘T’。
示例 2:
输入:answerKey = “TFFT”, k = 1
输出:3
解释:我们可以将最前面的 ‘T’ 换成 ‘F’,得到 answerKey = “FFFT”。
或者,我们可以将第二个 ‘T’ 换成 ‘F’,得到 answerKey = “TFFF”。
两种情况下,都有三个连续的 ‘F’。
示例 3:
输入:answerKey = “TTFTTFTT”, k = 1
输出:5
解释:我们可以将第一个 ‘F’ 换成 ‘T’,得到 answerKey = “TTTTTFTT”。
或者我们可以将第二个 ‘F’ 换成 ‘T’,得到 answerKey = “TTFTTTTT”。
两种情况下,都有五个连续的 ‘T’。
提示:
n == answerKey.length
1 <= n <= 5 * 10^4
answerKey[i] 要么是 ‘T’,要么是 ‘F’
1 <= k <= n
题解:
在指定字符的情况下,我们可以计算其最大连续数目。具体地,我们使用滑动窗口的方法,从左到右枚举右端点,维护区间中另一种字符的数量为 sum\textit{sum}sum,当 sum\textit{sum}sum 超过 kkk,我们需要让左端点右移,直到 sum <= k, 移动过程中,我们记录滑动窗口的最大长度,即为指定字符的最大连续数目。
本题的答案为分别指定字符为 TTT 和 FFF 时的最大连续数目的较大值。
滑动窗口, 不多解释了
ac代码👇
class Solution {
public:int maxConsecutiveChar(string& answerKey, int k, char ch) {int n = answerKey.length();int ans = 0;for (int left = 0, right = 0, sum = 0; right < n; right++) {sum += answerKey[right] != ch;while (sum > k) {sum -= answerKey[left++] != ch;}ans = max(ans, right - left + 1);}return ans;}int maxConsecutiveAnswers(string answerKey, int k) {return max(maxConsecutiveChar(answerKey, k, 'T'),maxConsecutiveChar(answerKey, k, 'F'));}
};觉得写的不错的话, 点个赞吧~
相关文章:

leetcode力扣 2024. 考试的最大困扰度
一位老师正在出一场由 n 道判断题构成的考试,每道题的答案为 true (用 ‘T’ 表示)或者 false (用 ‘F’ 表示)。老师想增加学生对自己做出答案的不确定性,方法是最大化有连续相同结果的题数。(…...
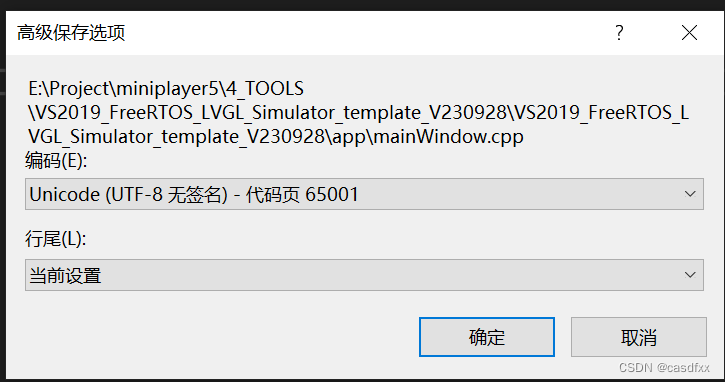
lvgl无法显示中文
环境: VS2019、LVGL8.3 问题: VS2019默认编码为GB2312, 解决: VS2022设置编码方式为utf-8的三种方式_vs utf8-CSDN博客 我用的方法2,设置为 utf-8无签名就行。...

读书笔记-Java并发编程的艺术-第1章 并发编程的挑战
文章目录 1.1 上下文切换1.1.1 多线程一定快吗1.1.2 如何减少上下文切换 1.2 死锁1.3 资源限制的挑战 1.1 上下文切换 即时是单核处理器也支持多线程执行代码,CPU通过给每个线程分配CPU时间片来实现这个机制。时间片是CPU分配给多个线程的时间,因为时间…...

RUST 和 GO 如何管理它们的内存
100编程书屋_孔夫子旧书网 Go 中的内存管理 Go 中的内存不会在缓存键被驱逐时立即释放。 相反,垃圾收集器会经常运行以发现任何没有引用的内存并释放它。 换句话说,内存会一直挂起,直到垃圾收集器可以评估它是否真正不再使用,而…...

对于高速信号完整性,一块聊聊啊(12)
常见的无源电子器件 电子系统中的无源器件可以按照所担当的电路功能分为电路类器件、连接类器件。 A、电路类器件: (1)二极管(diode) (2)电阻器(resistor) …...

C++学习笔记(19)——模板
目录 模板参数与非类型模板参数 模板参数 类型模板参数——传递类型 非类型模板参数——传递数量 C11希望array替代静态数组,但实际上vector包揽了一切 模板总结 优点: 缺点: 模板特化:针对某些类型进行特殊化处理 特化…...
java8新特性——函数式编程详解
目录 一 概述1.1 背景1.2 函数式编程的意义1.3 函数式编程的发展 Lambda表达式1.1 介绍1.2 使用Lambda的好处1.3 Lambda方法1.3.1 Lambda表达式结构1.3.2 Lambda表达式的特征 1.4 Lambda的使用1.4.1 定义函数式接口1.4.2 Lambda表达式实现函数式接口1.4.3 简化Lambda表达式1.4.…...

mybatis-plus小课堂: apply 拼接 in SQL,来查询从表某个范围内的数据
文章目录 引言I mybatis-Plus 之 apply 拼接 in SQL1.1 apply源码实现1.2 apply 拼接 in SQL : 非字符串数组1.3 apply 拼接 in SQL : 字符串数组II 如果in的数量太多,采用子查询。III 常见问题: Cause: comColumn xxx in where clause is ambiguoussee also引言 I mybati…...

民宿推荐系统-手把手调试搭建
民宿推荐系统-手把手调试搭建 民宿推荐系统-手把手调试搭建...
线性回归模型
目录 1.概述 2.线性回归模型的定义 3.线性回归模型的优缺点 4.线性回归模型的应用场景 5.线性回归模型的未来展望 6.小结 1.概述 线性回归是一种广泛应用于统计学和机器学习的技术,用于研究两个或多个变量之间的线性关系。在本文中,我们将深入探讨…...

西门子全球业务调整:数十亿欧元交易额,开启新篇章
导语 大家好,我是社长,老K。专注分享智能制造和智能仓储物流等内容。 新书《智能物流系统构成与技术实践》 导语 大家好,我是社长,老K。专注分享智能制造和智能仓储物流等内容。 在风起云涌的全球经济舞台上,西门子&am…...
AI遇上遥感,未来会怎样?
随着航空、航天、近地空间等多个遥感平台的不断发展,近年来遥感技术突飞猛进。由此,遥感数据的空间、时间、光谱分辨率不断提高,数据量也大幅增长,使其越来越具有大数据特征。对于相关研究而言,遥感大数据的出现为其提…...
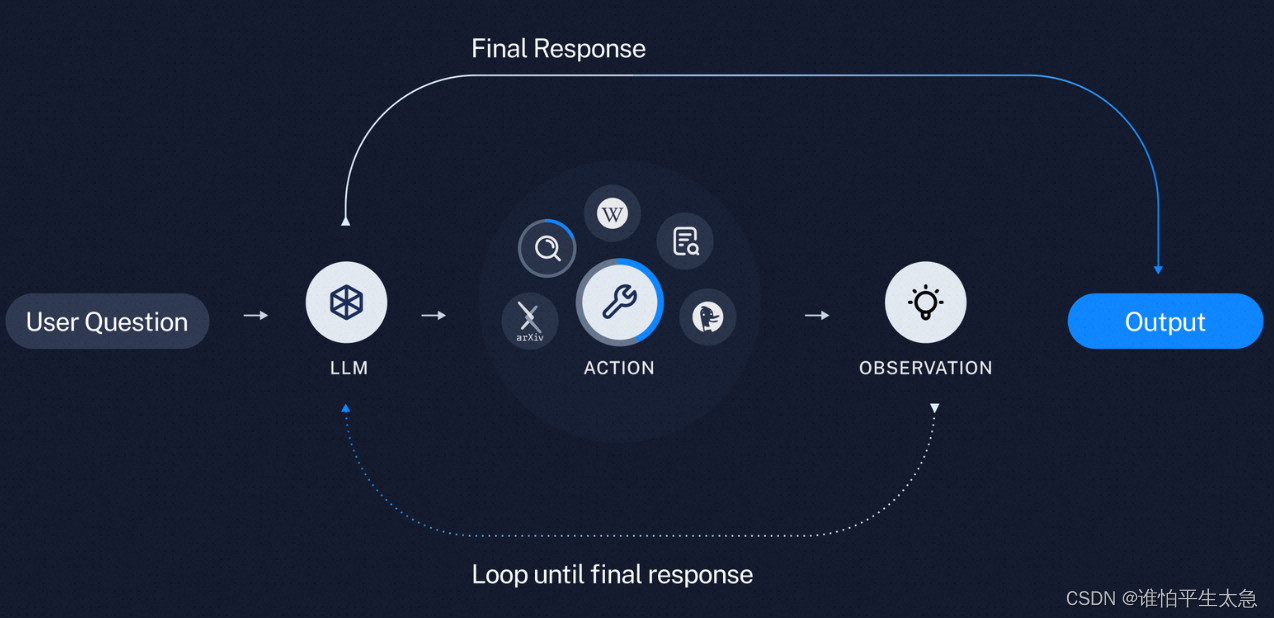
认知架构 cognitive architecture
Assistants API:以开发人员为中心。 有状态的API:允许存储以前的消息、上传文件、访问内置工具(代码解释器)、通过函数调用控制其他工具。 认知架构应用的两个组件:(1)如何提供上下文给应用 &…...

数据插值之朗格朗日插值(一)
目录 一、引言 二、代码实现 2.1 Lagrange插值求插值多项式: 代码解析: 1.vpa解释 2.ploy(x)解释: 3.conv()解释 4.poly2sym()解释 2.2 Lagrange插值求新样本值和误差估计: 代码解析&…...

【CCF-CSP】 202309-3 梯度求解
思路: 将表达式整理成只有目标求导变量的无括号加法表达式,其他变量均代入其值,然后利用最简单的求导公式,求出最终值。 样例1 x1 x1 x1 * x2 *转换成 x1*x1*x1x1*x2 若求导x1,则只留下x1,变为 x1*x1*x1…...
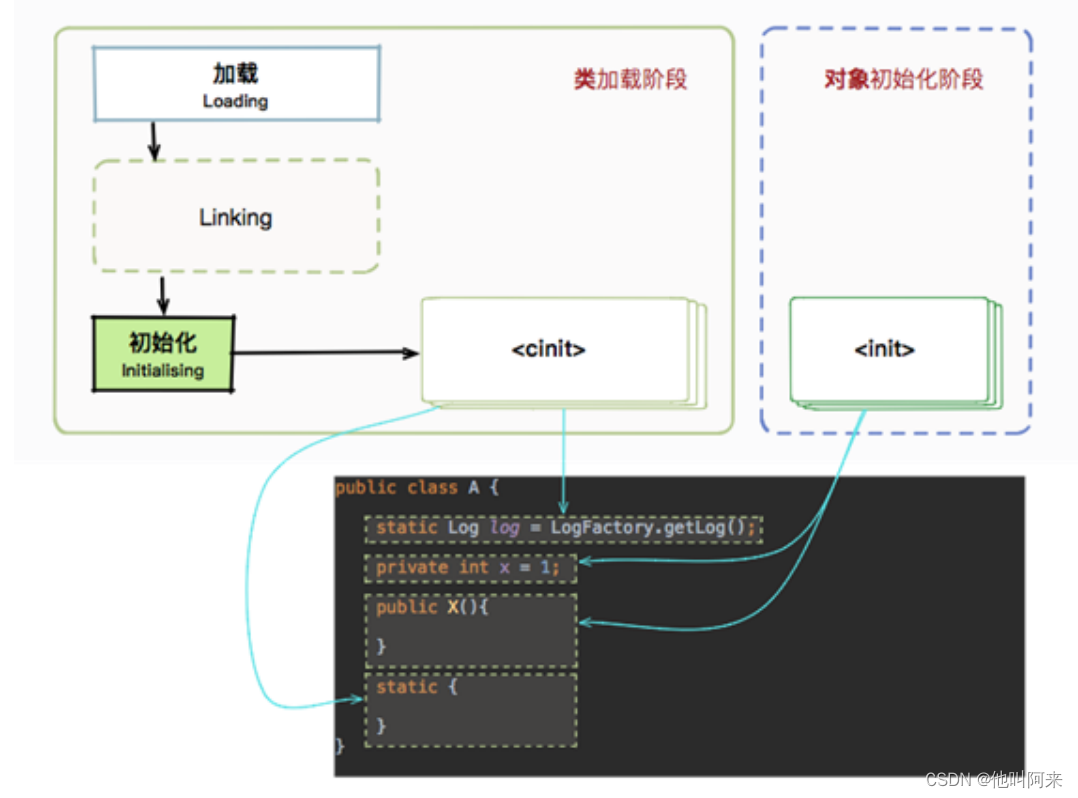
jvm的类加载
文章目录 概要加载类加载器分类双亲委派模型自定义加载器 验证准备解析初始化<cinit>与<init> 概要 jvm运行时的整体结构如下 一个Car类,类跟Car对象的转换过程如下: 加载后的class类信息存放于方法区;ClassLoader只负责clas…...

2024年汉字小达人活动4个多月开赛:18道历年选择题和答案、解析
根据近年的安排,2024年第11届汉字小达人比赛还有4个多月就启动,那么孩子们如何利用这段时间有条不紊地备考呢?我的建议是两手准备:①把小学1-5年级的语文课本上的知识点熟悉,重点是字、词、成语、古诗。②把历年真题刷…...

群晖安装青龙脚本
青龙定时任务管理面板,支持 Python3、JavaScript、Shell、Typescript 这几种环境,通过它可以方便的管理和运行定时任务(在某个时间执行一段代码),并且只需简单的配置,就可以在各个平台收到任务执行的结果通…...

【机器学习系列】使用高斯贝叶斯模型进行数据分类的完整流程
目录 一、导入数据 二、选择特征 三、十折交叉验证 四、划分训练集和测试集 五、训练高斯贝叶斯模型 六、预测测试集 七、查看训练集和测试集上的分数 八、查看混合矩阵 九、输出评估指标 一、导入数据 # 根据商户数据预测其是否续约案例 import pandas #读取数据到 da…...

Python中的单例模式:原理、实现与应用
Python中的单例模式:原理、实现与应用 一、引言 在软件开发中,设计模式是一种用于解决常见问题的最佳实践。单例模式(Singleton Pattern)是这些设计模式中的一种,它确保一个类仅有一个实例,并提供一个全局…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
