C++ 红黑树
目录
1.红黑树的概念
2.红黑树的性质
3.红黑树节点的定义
4.红黑树的插入操作
5.数据测试
1.红黑树的概念
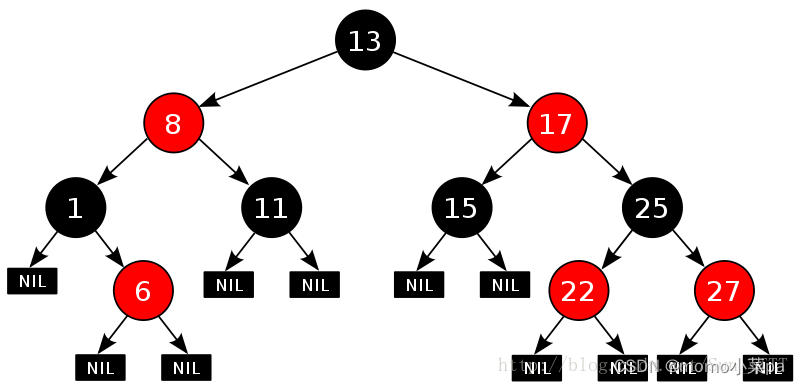
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的
2.红黑树的性质
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
思考:为什么满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍?
- 最短路径:由于性质4规定从任意节点到叶子节点的所有路径都包含相同数量的黑色节点,因此由纯黑色节点组成的路径将是最短路径。这是因为黑色节点是每条路径上必须包含的,而且没有其他颜色的节点可以“缩短”这条路径。
- 最长路径:最长路径将是由红色和黑色节点交替组成的路径。由于性质3禁止了连续红色节点的出现,因此最长路径将是黑色节点与红色节点交替出现的情况。由于每条路径上的黑色节点数量相同(性质4),红色节点的插入不会增加路径上黑色节点的数量,而是增加了路径的总长度。
- 路径长度比较:在最长路径中,每两个黑色节点之间可能插入一个红色节点,这使得最长路径的长度大致为最短路径(纯黑色节点)的两倍。这是因为在保持黑色节点数量相同的情况下,红色节点的插入只是在黑色节点之间增加了额外的节点,而这些额外的红色节点最多只能使路径长度加倍。
3.红黑树节点的定义
enum Colour {RED,BLACK };template<class K, class V> struct RBTreeNode {RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){} };template<class K, class V> class RBTree {typedef RBTreeNode<K, V> Node;private:Node* _root = nullptr; };
- 成员变量:
_left、_right和_parent分别指向节点的左子节点、右子节点和父节点。_kv是一个pair<K, V>,存储节点的键和值。_col表示节点的颜色,可以是RED或BLACK。- 构造函数:
接收一个pair<K, V>作为参数,初始化节点的键值对,并将节点的颜色初始化为RED。其他指针成员初始化为nullptr。
4.红黑树的插入操作
我们在进行插入操作时,新节点默认是红色。红色节点的插入可能导致红黑树的性质被破坏,但通过将新节点设为红色,我们可以更容易地通过颜色变换和旋转来恢复平衡。具体来说,红色节点的插入只会影响局部区域的平衡,而黑色节点的插入则可能影响整棵树的平衡。
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何
性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连
在一起的红色节点,此时需要对红黑树分情况来讨论:
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
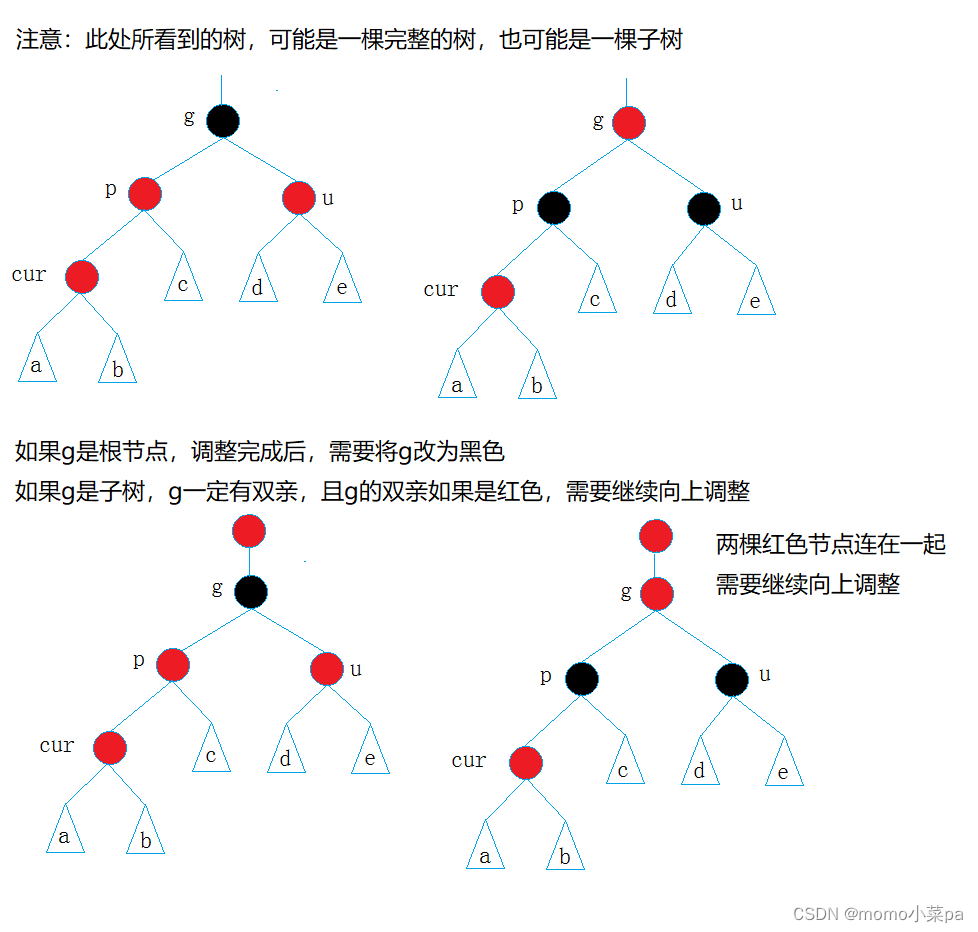
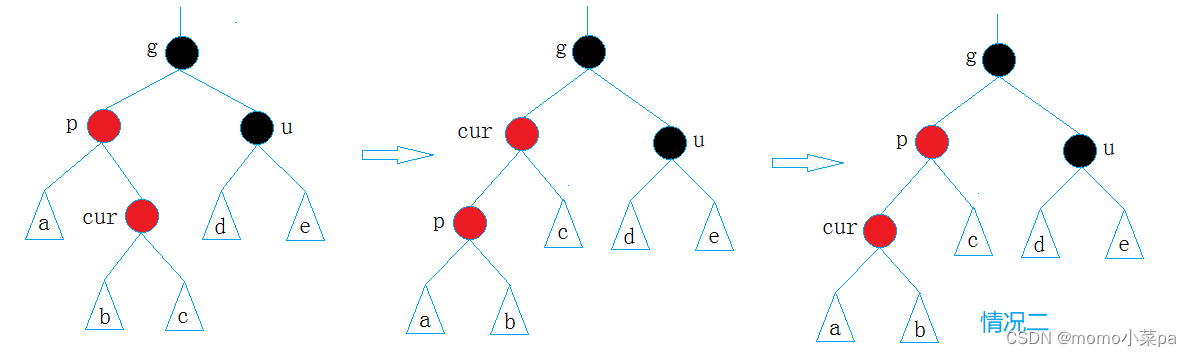
情况一: cur为红,p为红,g为黑,u存在且为红情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑
p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,
p为g的右孩子,cur为p的右孩子,则进行左单旋转
p、g变色--p变黑,g变红
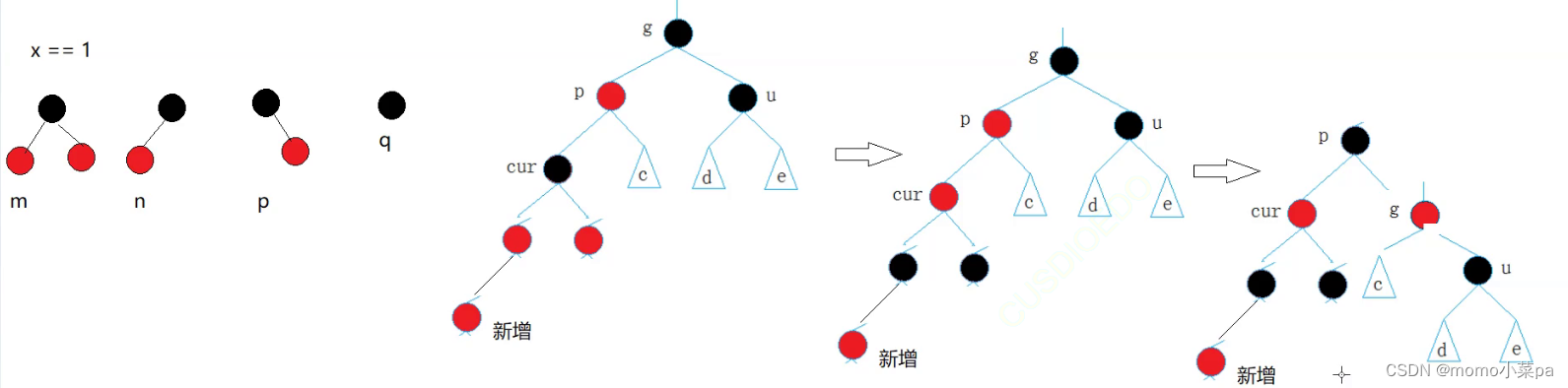
情况三: cur为红,p为红,g为黑,u不存在/u存在且为黑(双旋)
p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;相反,
p为g的右孩子,cur为p的左孩子,则针对p做右单旋转
则转换成了情况2
针对每种情况进行相应的处理即可。据以上情况写代码:
}cur = new Node(kv);cur->_col = RED; // 新增节点给红色if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// parent的颜色是黑色也结束while (parent && parent->_col == RED){// 关键看叔叔Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;// 叔叔存在且为红,-》变色即可if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else // 叔叔不存在,或者存在且为黑{if (cur == parent->_left){// g // p u// c RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g // p u// c RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;// 叔叔存在且为红,-》变色即可if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else // 叔叔不存在,或者存在且为黑{// 情况二:叔叔不存在或者存在且为黑// 旋转+变色// g// u p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}代码解释:
- 初始化新节点:
- 创建一个新的节点
cur,并为其分配键值对kv。- 将新节点的颜色设置为红色(RED),因为在红黑树的规则中,新插入的节点默认为红色。
- 根据键值对的大小,将新节点插入到其父节点的左子树或右子树。
- 设置新节点的父节点。
- 调整红黑树以保持其性质:
- 如果父节点是黑色的,那么不需要进行任何调整,因为插入红色节点不会违反红黑树的性质。
- 如果父节点是红色的,那么需要进行调整以恢复红黑树的性质。这是通过一个循环来完成的,该循环会持续进行,直到父节点不再是红色或者已经进行了必要的调整。
- 调整过程:
- 首先,根据父节点是其祖父节点的左子节点还是右子节点,分为两种情况处理。
- 在每种情况下,都会考虑叔叔节点的颜色和存在性。
- 如果叔叔节点是红色的,那么可以通过重新着色父节点、叔叔节点和祖父节点来恢复红黑树的性质,然后将当前节点移动到祖父节点,并更新父节点为祖父节点的父节点,继续向上调整。
- 如果叔叔节点是黑色的或者不存在,那么需要进行旋转操作来恢复红黑树的性质。根据当前节点是父节点的左子节点还是右子节点,进行相应的旋转操作,并重新着色节点。
- 结束调整:
- 一旦退出调整循环,将根节点着色为黑色,以确保红黑树的根节点总是黑色的性质。
以下是旋转逻辑的代码示例:
void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppNode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppNode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_right == parent){ppNode->_right = subR;}else{ppNode->_left = subR;}subR->_parent = ppNode;}}
5.数据测试
为了更好的测试数据,我们需要写一个检查一棵红黑树是否满足红黑树的性质,以确保红黑树的正确性:
bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){//cout << blackNum << endl;if (refNum != blackNum){cout << "存在黑色节点的数量不相等的路径" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红色节点" << endl;return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);}代码解释:
空节点检查:
- 如果
root是空指针(即已经到达了一个叶节点),函数会检查当前路径上的黑色节点数量blackNum是否与参考数量refNum相等。- 如果不相等,会输出错误信息,并返回
false,表示检查失败。- 如果相等,则返回
true,表示这条路径满足红黑树的性质。连续红色节点检查:
- 如果当前节点的颜色是红色,并且其父节点的颜色也是红色,那么会输出错误信息,并返回
false。因为红黑树的一个关键性质是不允许有两个连续的红色节点。黑色节点计数:
- 如果当前节点的颜色是黑色,
blackNum会递增,以记录从根节点到当前节点的路径上黑色节点的数量。递归检查:
- 函数会递归地对左子树和右子树进行相同的检查。
- 如果左右子树都满足红黑树的性质(即递归调用都返回
true),则整个子树满足性质,函数返回true。- 如果有任何一个子树不满足性质,函数返回
false。下面是红黑树的完整代码:
enum Colour {RED,BLACK };template<class K, class V> struct RBTreeNode {RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){} };template<class K, class V> class RBTree {typedef RBTreeNode<K, V> Node; public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED; // 新增节点给红色if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// parent的颜色是黑色也结束while (parent && parent->_col == RED){// 关键看叔叔Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;// 叔叔存在且为红,-》变色即可if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else // 叔叔不存在,或者存在且为黑{if (cur == parent->_left){// g // p u// c RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g // p u// c RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;// 叔叔存在且为红,-》变色即可if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else // 叔叔不存在,或者存在且为黑{// 情况二:叔叔不存在或者存在且为黑// 旋转+变色// g// u p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppNode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppNode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_right == parent){ppNode->_right = subR;}else{ppNode->_left = subR;}subR->_parent = ppNode;}}void InOrder(){_InOrder(_root);cout << endl;}bool IsBalance(){if (_root->_col == RED){return false;}int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);}private:bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){//cout << blackNum << endl;if (refNum != blackNum){cout << "存在黑色节点的数量不相等的路径" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红色节点" << endl;return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}private:Node* _root = nullptr; };数据测试:
void TestRBTree1() {int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14,8, 3, 1, 10, 6, 4, 7, 14, 13 };RBTree<int, int> t1;for (auto e : a){if (e == 10){int i = 0;}t1.Insert({ e,e });cout << "Insert:" << e << "->" << t1.IsBalance() << endl;}t1.InOrder();cout << t1.IsBalance() << endl; }
符合预期,代码正确。
相关文章:

C++ 红黑树
目录 1.红黑树的概念 2.红黑树的性质 3.红黑树节点的定义 4.红黑树的插入操作 5.数据测试 1.红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个…...

PTA 6-4 配对问题
许多大学生报名参与大运会志愿者工作。其中运动场引导员需要男女生组队,每组一名男生加一名女生,男生和女生各自排成一队,依次从男队和女队队头各出一人配成小组,若两队初始人数不同,则较长那一队未配对者调到其他志愿…...

sklearn基础教程
scikit-learn是一个用于机器学习的Python库,提供了多种机器学习的方法和模型,以及数据预处理、特征选择、模型评估等功能。它简化了机器学习流程,并且具有易于使用和灵活的特点。 本教程将介绍sklearn的基础知识和常用功能,帮助你…...

MySQL入门学习-查询进阶.别名
别名(Alias)是为数据库中的表、列或表达式赋予的一个临时名称。使用别名可以使查询结果更具可读性,并且在复杂的查询中更方便地引用和处理数据。 在 MySQL 中,别名可以通过 AS 关键字来定义,例如: SELECT…...

【Rust日报】嵌入式 Rust:一份简化指南
EvilHelix 编辑器 EvilHelix 是一个采用 Vim 风格的模态编辑器,旨在提供快速且高效的编辑体验。它是 Helix 编辑器的一个分支,增加了 Vim binding,同时积极同步上游的特性,兼备了 Vim 和 Hexli 的优点: Vim 风格的模态…...

Web课外练习9
<!DOCTYPE html> <html> <head><meta charset"utf-8"><title>邮购商品业务</title><!-- 引入vue.js --><script src"./js/vue.global.js" type"text/javascript"></script><link rel&…...

rtsp协议分析
rtsp (real-time stream protocol)实时流媒体控制协议 属于基于文本的应用层协议,rtsp的底层协议可以是udp也可以是tcp ffmpeg 参数-rtsp_transport tcp 用于指定RTSP会话底层传输协议为TCP 本身并不传输流媒体数据,只是提供流媒体的控制,实…...
Spring Web MVC(2)
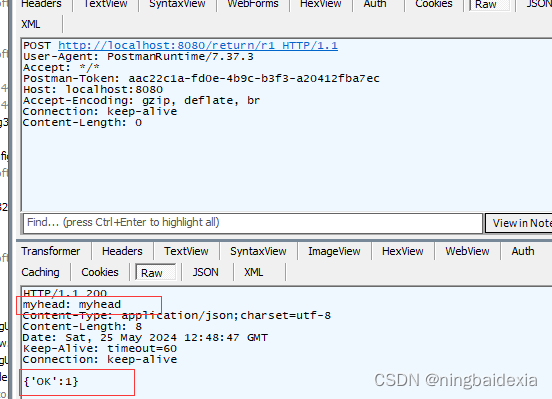
响应 Http响应的结果可以是数据也可以是静态页面可以针对响应设置状态码 Header信息 返回静态页面注解RestController和Controller 我们创建一个前端页面 package com.example.demo.demos.web.controller;import org.springframework.web.bind.annotation.RequestMapping; i…...

Python-图片旋转360,保存对应图片
#Author :susocool #Creattime:2024/5/25 #FileName:turn360 #Description: 会旋转指定的图像文件360度,并将每个旋转后的图像保存到指定目录,文件名以旋转角度命名。 from PIL import Imagedef rotate_and_save(image_path, output_dir) :# …...

JavaSE——集合框架二(1/6)-前置知识-可变参数、Collections工具类
目录 可变参数 Collections工具类 Collections的常用静态方法 实例演示 可变参数 可变参数 就是一种特殊形参,定义在方法、构造器的形参列表里,格式是:数据类型...参数名称 可变参数的特点和好处 特点:可以不传数据给它&am…...

我用LLaMA-Factory微调大模型来实现商品评论情感分析,准确率高达91.70%
大家好,我是程序锅。 最近在modelscope上闲逛的时候,在数据集板块发现有一个商品评论情感预测数据集。这个数据集源自一个比赛,它的目的是为了预测电商平台顾客的评论是好评还是差评。 数据示例如下所示(其中0代表差评ÿ…...

四大进制--详解--以及进制转换规则
进制介绍 对于整数, 有四种表达方式: 二进制BIN: 0,1 , 满2进1.以0b或0B开头 所谓2进制就是使用0和1来表示一个数, 满2进1如果在开发中看到有这种写法: int n1 0b1010; 这种写法没有错, 这是二进制的一种表示方式 十进制DEC: 0-9, 满10进1 十进制就是0-9来表示一个数, 满10进…...

谈谈API和人工智能领域的开发和使用以及AI大模型开发进程。
API,全称为Application Programming Interface,即应用程序编程接口,是一些预先定义的函数。 它的主要目的是提供应用程序与开发人员基于某软件或硬件得以访问一组例程的能力,而无需访问源码,或理解内部工作机制的细节。API函数包含在操作系统的动态连接库文件中,例如Win…...
用Python Pygame做的一些好玩的小游戏
有些游戏的代码比较长就不公布了 1.简简单单 1.疯狂的鸡哥 你要准备的图片: 命名为:ji.png 代码: import pygame import random as r pygame.init() pygame.display.set_caption(aaa) pm pygame.display.set_mode((800,600))class Ls(py…...

【吊打面试官系列】Java高并发篇 - ThreadLocal 是什么?有什么用?
大家好,我是锋哥。今天分享关于 【ThreadLocal 是什么?有什么用?】面试题,希望对大家有帮助; ThreadLocal 是什么?有什么用? ThreadLocal 是一个本地线程副本变量工具类。主要用于将私有线程和该…...
)
Spring MVC的数据转换及数据格式化:java 转换器接口(将一种类型的对象转换为另一种类型及其子类对象)
文章目录 引言I 将String转为BaseEnum的子类对象1.1 注册转换器工厂1.2 实现转换器工厂1.3 实现转换器接口 `interface Converter<S, T> `1.4 根据枚举code和type获取枚举II 枚举2.1 枚举接口2.2 枚举子类2.3 请求实体引言 Spring MVC的数据转换及数据格式化 应用场景:…...
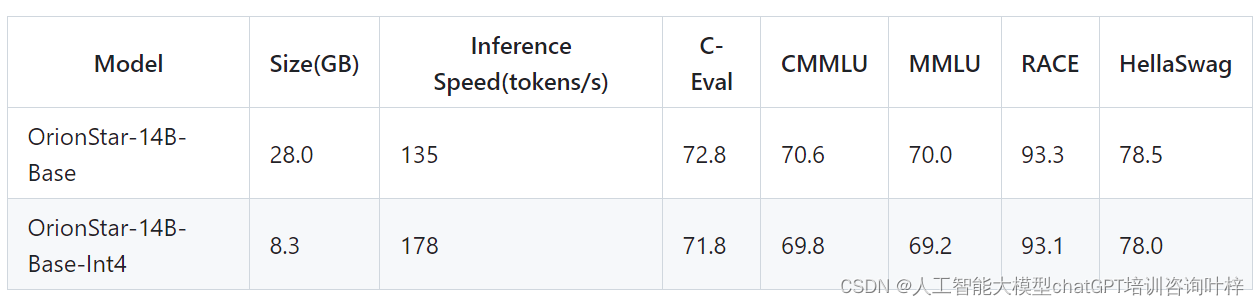
【开源】多语言大型语言模型的革新:百亿参数模型超越千亿参数性能
大型人工智能模型,尤其是那些拥有千亿参数的模型,因其出色的商业应用表现而受到市场的青睐。但是,直接通过API使用这些模型可能会带来数据泄露的风险,尤其是当模型提供商如OpenAI等可能涉及数据隐私问题时。私有部署虽然是一个解决…...

DDL—表—数据类型—日期时间类型相关语法
(1)表格如下: 类型大小范围格式描述DATE31000-01-01 至 9999-12-31YYYY-MM-DD日期值(年月日)TIME3-838:59:59 至 838:59:59HH:MM:SS时间值或持续时间(时分秒)YEAR11901 至 2155YYYY年份值DATET…...
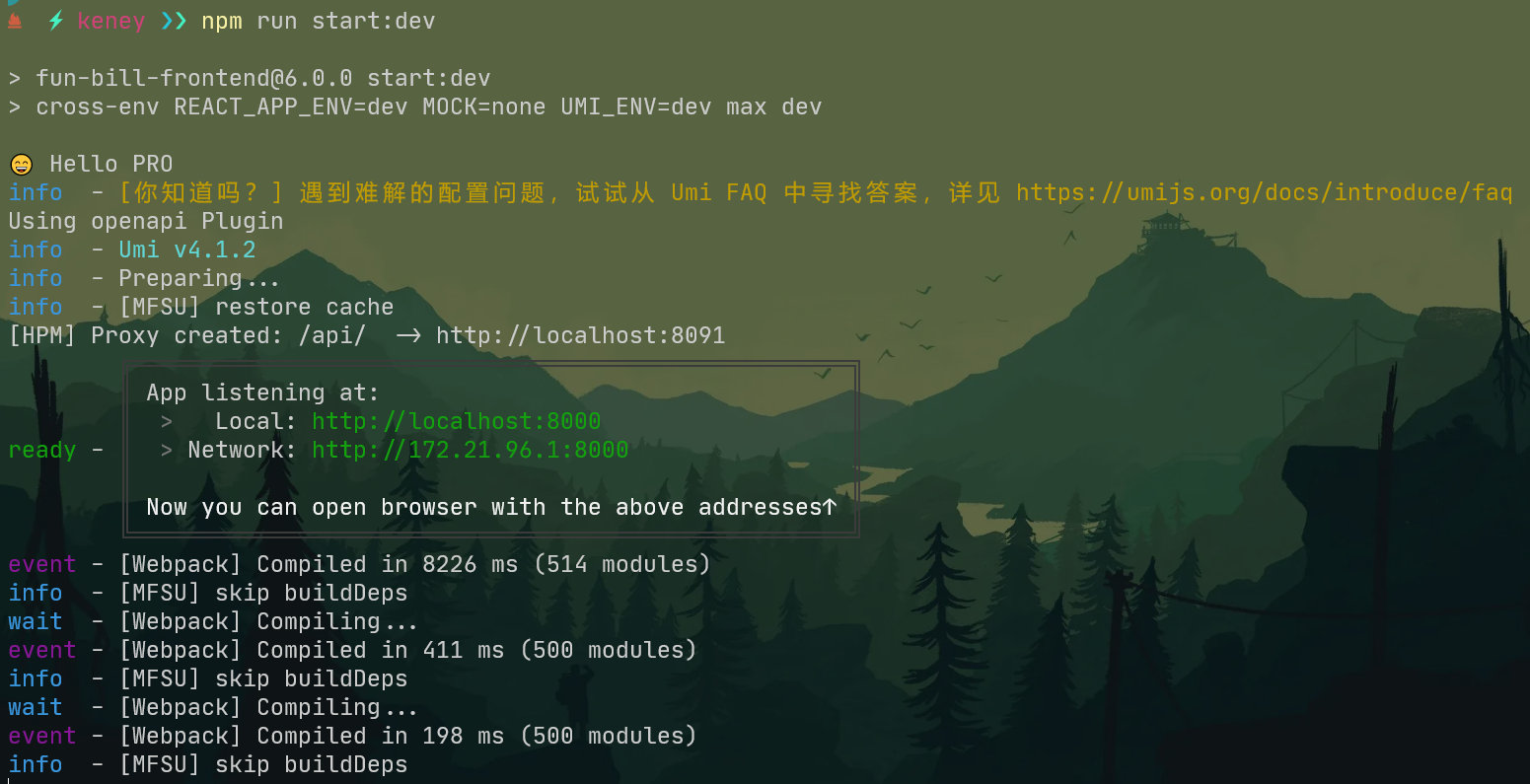
Ant Design pro 6.0.0 搭建使用以及相关配置
一、背景 在选择一款比较合适的中台的情况下,挑选了有arco design、ant design pro、soybean、vue-pure-admin等中台系统,经过筛选就选择了ant design pro。之前使用过arco design 搭建通过组件库拼装过后台管理界面,官方文档也比较全&#…...

Vue生命周期钩子是如何实现的
Vue的生命周期钩子是在Vue组件创建、挂载、更新、销毁等过程中自动调用的特殊函数。这些钩子允许开发者在组件的不同阶段执行特定的逻辑。Vue 2 和 Vue 3 在生命周期钩子上有一些差异,主要是因为Vue 3引入了Composition API和更现代的JavaScript特性。 Vue 2 的生命…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...