动态规划之背包问题中如何确定遍历顺序的问题-组合or排列?
关于如何确定遍历顺序
322. 零钱兑换中,本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
所以本题并不强调集合是组合还是排列。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
在动态规划专题我们讲过了求组合数是动态规划:518.零钱兑换II (opens new window),求排列数是动态规划:377. 组合总和 Ⅳ (opens new window)。
所以本题的两个for循环的关系是:外层for循环遍历物品,内层for遍历背包或者外层for遍历背包,内层for循环遍历物品都是可以的!
那么我采用coins放在外循环,target在内循环的方式。
本题钱币数量可以无限使用,那么是完全背包。所以遍历的内循环是正序
综上所述,遍历顺序为:coins(物品)放在外循环,target(背包)在内循环。且内循环正序。
求组合数
例题:518.零钱兑换II
这是一道典型的背包问题,一看到钱币数量不限,就知道这是一个完全背包。
但本题和纯完全背包不一样,纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物品组合个数!
注意题目描述中是凑成总金额的硬币组合数,为什么强调是组合数呢?
例如示例一:
5 = 2 + 2 + 1
5 = 2 + 1 + 2
这是一种组合,都是 2 2 1。
如果问的是排列数,那么上面就是两种排列了。
组合不强调元素之间的顺序,排列强调元素之间的顺序。 其实这一点我们在讲解回溯算法专题的时候就讲过了哈。
那我为什么要介绍这些呢,因为这和下文讲解遍历顺序息息相关!
- 确定遍历顺序
本题中我们是外层for循环遍历物品(钱币),内层for遍历背包(金钱总额),还是外层for遍历背包(金钱总额),内层for循环遍历物品(钱币)呢?
我在动态规划:关于完全背包,你该了解这些! (opens new window)中讲解了完全背包的两个for循环的先后顺序都是可以的。
但本题就不行了!
因为纯完全背包求得装满背包的最大价值是多少,和凑成总和的元素有没有顺序没关系,即:有顺序也行,没有顺序也行!
而本题要求凑成总和的组合数,元素之间明确要求没有顺序。
所以纯完全背包是能凑成总和就行,不用管怎么凑的。
本题是求凑出来的方案个数,且每个方案个数是为组合数。
那么本题,两个for循环的先后顺序可就有说法了。
我们先来看 外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)的情况。
代码如下:
for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量dp[j] += dp[j - coins[i]];}
}假设:coins[0] = 1,coins[1] = 5。
那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。
所以这种遍历顺序中dp[j]里计算的是组合数!
如果把两个for交换顺序,代码如下:
for (int j = 0; j <= amount; j++) { // 遍历背包容量for (int i = 0; i < coins.size(); i++) { // 遍历物品if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];}
}背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。
此时dp[j]里算出来的就是排列数!
可能这里很多同学还不是很理解,建议动手把这两种方案的dp数组数值变化打印出来,对比看一看!(实践出真知)
2.举例推导dp数组
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:

求排列数
例题:377. 组合总和 Ⅳ
本题题目描述说是求组合,但又说是可以元素相同顺序不同的组合算两个组合,其实就是求排列!
弄清什么是组合,什么是排列很重要。
组合不强调顺序,(1,5)和(5,1)是同一个组合。
排列强调顺序,(1,5)和(5,1)是两个不同的排列。
但其本质是本题求的是排列总和,而且仅仅是求排列总和的个数,并不是把所有的排列都列出来。
如果本题要把排列都列出来的话,只能使用回溯算法爆搜。
- 确定遍历顺序
个数可以不限使用,说明这是一个完全背包。
得到的集合是排列,说明需要考虑元素之间的顺序。
本题要求的是排列,那么这个for循环嵌套的顺序可以有说法了。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
如果把遍历nums(物品)放在外循环,遍历target的作为内循环的话,举一个例子:计算dp[4]的时候,结果集只有 {1,3} 这样的集合,不会有{3,1}这样的集合,因为nums遍历放在外层,3只能出现在1后面!
所以本题遍历顺序最终遍历顺序:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前到后遍历。
2.举例来推导dp数组

class Solution {public int combinationSum4(int[] nums, int target) {// 初始化dp数组,dp[i]表示目标和为i的所有组合数int[] dp = new int[target + 1];// 目标和为0时只有一种情况,即不选择任何元素dp[0] = 1;// 遍历每个从0到target的值for (int i = 0; i <= target; i++) { //遍历背包// 对于每个值i,遍历数组中的每个数for (int j = 0; j < nums.length; j++) { //遍历物品// 如果当前值i大于等于数组中的数nums[j]if (i >= nums[j]) { //背包容量大于物品重量// 将dp[i - nums[j]]的值加到dp[i]中// 这意味着通过添加nums[j]到组合中,我们找到了新的组合数//dp[i] += dp[i - nums[j]];dp[i] = dp[i] + dp[i - nums[j]]; }}}// 返回dp[target],即目标和为target的所有组合数return dp[target];}
}
- 时间复杂度: O(target * n),其中 n 为 nums 的长度
- 空间复杂度: O(target)
C++测试用例有两个数相加超过int的数据,所以需要在if里加上dp[i] < INT_MAX - dp[i - num]。
但java就不用考虑这个限制,java里的int也是四个字节吧,也有可能leetcode后台对不同语言的测试数据不一样。
总结
细心的同学看网上的题解,可能看一篇是遍历背包的for循环放外面,看一篇又是遍历背包的for循环放里面,看多了都看晕了,到底两个for循环应该是什么先后关系。
能把遍历顺序讲明白的文章几乎找不到!
这也是大多数同学学习动态规划的苦恼所在,有的时候递推公式很简单,难在遍历顺序上!
但最终又可以稀里糊涂的把题目过了,也不知道为什么这样可以过,反正就是过了。
那么这篇文章就把遍历顺序分析的清清楚楚。
动态规划:518.零钱兑换II (opens new window)中求的是组合数,动态规划:377. 组合总和 Ⅳ (opens new window)中求的是排列数。
而本题是要求最少硬币数量,硬币是组合数还是排列数都无所谓!所以两个for循环先后顺序怎样都可以!
这也是我为什么要先讲518.零钱兑换II 然后再讲本题即:322.零钱兑换,这是Carl的良苦用心那。
相信大家看完之后,对背包问题中的遍历顺序有更深的理解了。
相关文章:

动态规划之背包问题中如何确定遍历顺序的问题-组合or排列?
关于如何确定遍历顺序 322. 零钱兑换中,本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。 所以本题并不强调集合是组合还是排列。 如果求组合数就是外层for循环遍历物品,内层for遍历背包。 如果求…...

开源大模型与闭源大模型
概述 开源大模型和闭源大模型是两种常见的大模型类型,它们在以下方面存在差异: 开放性: 开源大模型:代码和模型结构是公开可用的,任何人都可以访问、修改和使用。闭源大模型:模型的代码和结构是私有的&…...

python+selenium - UI自动框架之封装查找元素
单一的元素定位方法不能满足所有元素的定位,可以根据每个元素的特点来找到合适的方法,可以参考下图的方法: elementFind.py from selenium.webdriver.support.ui import WebDriverWait from selenium.webdriver.support import expected_con…...
java 拦截器-用户无操作超时退出利用Redis
1、授权过滤,只要实现AuthConfigAdapter接口 2、利用Redis token超时时间,用户访问后台续时 效果 Component public class AuthFilter implements Filter {private static Logger logger LoggerFactory.getLogger(AuthFilter.class);Autowiredprivat…...

民国漫画杂志《时代漫画》第16期.PDF
时代漫画16.PDF: https://url03.ctfile.com/f/1779803-1248612470-6a05f0?p9586 (访问密码: 9586) 《时代漫画》的杂志在1934年诞生了,截止1937年6月战争来临被迫停刊共发行了39期。 ps:资源来源网络!...

线程池以及日志类的实现
目录 线程池: 日志类: 可变参数以及相关函数 1.va_list 2. va_start 3. va_end 日志Log类 线程池 线程池: 是一种线程使用模式。线程过多会带来调度开销,进而影响缓存局部性和整体性能。而线程池维护着多个线程,等待着 监督管理者分配可并发执行…...

基于长短期记忆网络 LSTM 的送餐时间预测
前言 系列专栏:【深度学习:算法项目实战】✨︎ 涉及医疗健康、财经金融、商业零售、食品饮料、运动健身、交通运输、环境科学、社交媒体以及文本和图像处理等诸多领域,讨论了各种复杂的深度神经网络思想,如卷积神经网络、循环神经网络、生成对…...

K-means聚类算法详细介绍
目录 🍉简介 🍈K-means聚类模型详解 🍈K-means聚类的基本原理 🍈K-means聚类的算法步骤 🍈K-means聚类的优缺点 🍍优点 🍍缺点 🍈K-means聚类的应用场景 🍈K-mea…...
SAP FS00如何导出会计总账科目表
输入T-code : S_ALR_87012333 根据‘FS00’中找到的总账科目,进行筛选执行 点击左上角的列表菜单,选择‘电子表格’导出即可...

ROS参数服务器
一、介绍 参数服务器是用于存储和检索参数的分布式多机器人配置系统,它允许节点动态地获取参数值。 在ROS中,参数服务器是一种用于存储和检索参数的分布式多机器人配置系统。它允许节点动态地获取参数值,并提供了一种方便的方式来管理和共享配…...

QCC---DFU升级变更设备名和地址
QCC---DFU升级变更设备名和地址 这个很多人碰到这个疑问,升级了改不了设备名和地址 /******************************************************************************* Copyright (c) 2018 Qualcomm Technologies International, Ltd. FILE NAME sink_dfu_ps.c DESCRIPT…...

[力扣题解] 695. 岛屿的最大面积
题目:695. 岛屿的最大面积 思路 代码 深度优先搜索 // 深度搜索 class Solution { private:int area_max 0;int dir[4][2] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};void dfs(vector<vector<int>>& grid, vector<vector<bool>>& …...

AI模型发展路径探析:开源与闭源,何者更胜一筹?
AI模型发展路径探析:开源与闭源,何者更胜一筹? 在当今快速发展的人工智能领域,AI模型成为推动技术创新和应用落地的关键。而评价一个AI模型“好不好”“有没有发展”,往往会引向一个重要话题:开源与闭源这…...

concurrency 并行编程
Goroutine go语言的魅力所在,高并发。 线程是操作系统调度的一种执行路径,用于在处理器执行我们在函数中编写的代码。一个进程从一个线程开始,即主线程,当该线程终止时,进程终止。这是因为主线程是应用程序的原点。然后…...

JavaScript如何让一个按钮的点击事件在完成之前禁用
在JavaScript中,要禁用一个按钮的点击事件直到某个操作完成,你可以将其点击事件用匿名函数的方式书写。 你可以将其在点击函数内设置为null来禁用按钮。 <button id"butto_n">点击抽奖</button><script>butto_n.onclick bu…...

透视App投放效果,Xinstall助力精准分析,让每一分投入都物超所值!
在移动互联网时代,App的推广与投放成为了每一个开发者和广告主必须面对的问题。然而,如何精准地掌握投放效果,让每一分投入都物超所值,却是一个令人头疼的难题。今天,我们就来谈谈如何通过Xinstall这个专业的App全渠道…...

【Linux杂货铺】进程通信
目录 🌈 前言🌈 📁 通信概念 📁 通信发展阶段 📁 通信方式 📁 管道(匿名管道) 📂 接口 编辑📂 使用fork来共享通道 📂 管道读写规则 &…...
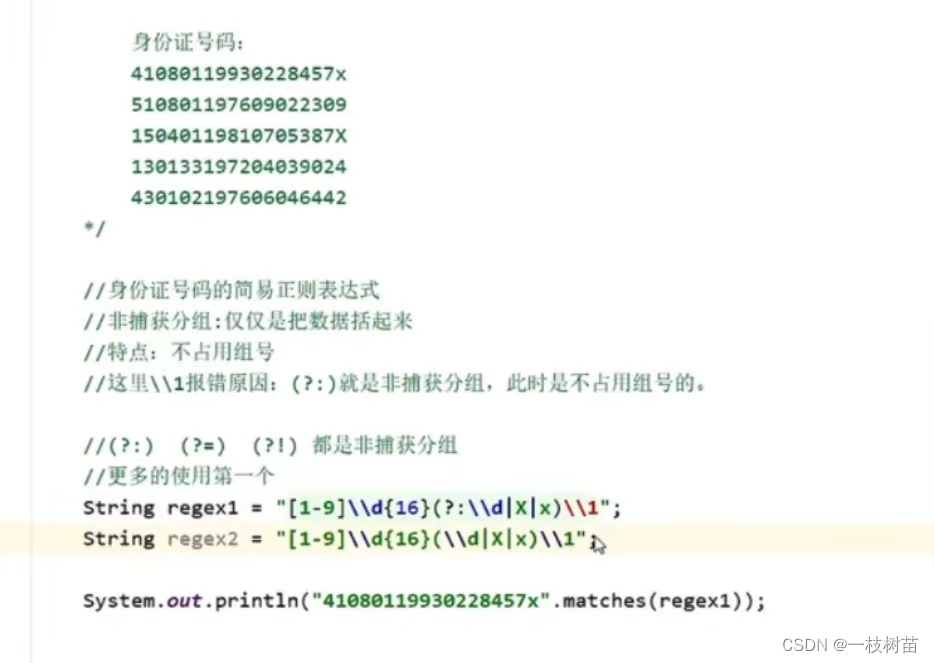
常用API(正则表达式、爬取、捕获分组和非捕获分组 )
1、正则表达式 练习——先爽一下正则表达式 正则表达式可以校验字符串是否满足一定的规则,并用来校验数据格式的合法性。 需求:假如现在要求校验一个qq号码是否正确。 规则:6位及20位之内,0不能在开头,必须全部是数字…...
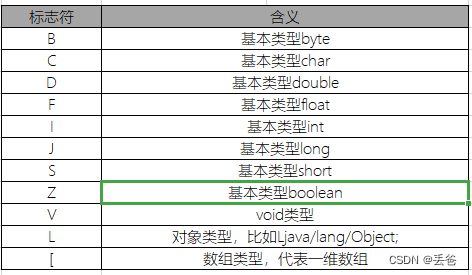
JVM学习-Class文件结构②
访问标识(access_flag) 在常量池后,紧跟着访问标记,标记使用两个字节表示,用于识别一些类或接口层次的访问信息,包括这个Class是类还是接口,是否定义为public类型,是否定义为abstract类型,如果…...

数据库连接项目
MySQL...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
