堆(建堆算法,堆排序)
目录
一.什么是堆?
1.堆
2.堆的储存
二.堆结构的创建
1.头文件的声明:
2.向上调整
3.向下调整
4.源码:
三.建堆算法
1.向上建堆法
2.向下建堆法
四.堆排序
五.在文件中Top出最小的K个数
一.什么是堆?
1.堆
堆就是完全二叉树,而且是一种特殊的完全二叉树,它需要满足每一个父节点都大于子节点,称为大堆,或每一个父节点都小于子节点,称为小堆。而对兄弟节点之间的大小关系并没有要求(为此它并不是有序的)。如下:

2.堆的储存
对于完全二叉树有一个更好的储存方法,就是用顺序表来储存,相比链式储存使用顺序表储存的一个很大的好处在于知道一个结点可以很容易的算出它父结点和子结点的下标,还有可以随机访问。

父子结点下标计算公式 :
左子结点下标 = 父结点下标*2+1
右子结点下标 = 父结点下标*2+2
父结点下标 = (子结点下标-1) / 2
二.堆结构的创建
1.头文件的声明:
Heap.h
#pragma
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#define HpDataType int
typedef int HPDataType;
typedef struct Heap
{HPDataType* arr;int size;int cap;
}Heap;
void HeapInit(Heap* php);//堆的初始化
void HeapDestory(Heap* hp);//堆的销毁
void HeapPush(Heap* hp, HPDataType x);//堆的插入
void HeapPop(Heap* hp);//堆的删除
HPDataType HeapTop(Heap* hp);//取堆顶的数据
int HeapSize(Heap* hp);//堆的数据个数
int HeapEmpty(Heap* hp);//堆的判空void AdjustUP(HpDataType* arr, int child);//向上调整
void AdjustDOWN(HpDataType* arr, int size, int parent);//向下调整
void Swap(HpDataType* a, HpDataType* b);//元素的交换其中堆的初始化,堆的销毁,堆的数据个数,堆的判空,和取堆顶数据和顺序表的操作是一样的这里重点来学一下堆的插入,堆的删除。
2.向上调整
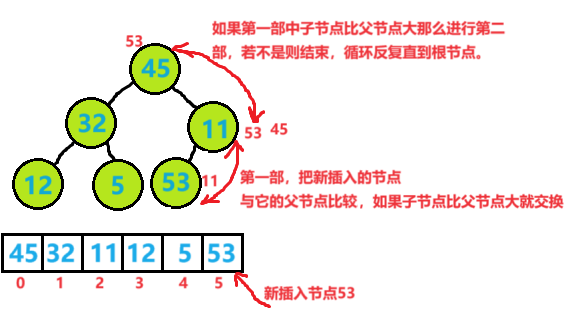
插入元素呢直接往数组最后插入就可以,但是插入后就不一定是堆结构的,所以需要调整。例如一个大堆:
向大堆中插入53
调整后:
代码示例:
void AdjustUP(HpDataType* arr,int child) {int parent = (child - 1) / 2;//计算父节点下标while (child>0)//注意这里不能是parent>0{if (arr[child] > arr[parent]){Swap(&arr[child], &arr[parent]);//封装一个函数进行交换child = parent;//更新子节点parent = (child - 1) / 2;//更新父节点}elsebreak;} }★如果是小堆只需要把if条件的大于号改为小于号
3.向下调整
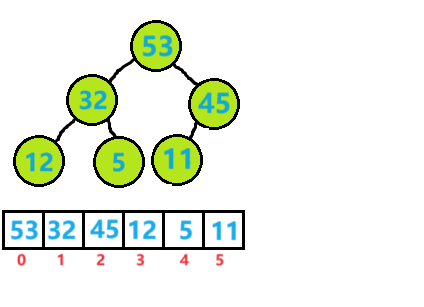
要注意删除元素我们删除的不是尾元素,这样毫无意义,我们删除的是下标为0位置的元素,它是整个堆中最小或最大的元素。怎么删除呢?直接将它删除然后后面的元素在覆盖上吗?这样做的话,它就不是堆了,而且元素之间关系将会全部混乱,就需要从0开始创建堆,效率非常低,我们可以把首元素与尾元素互换然后删除尾元素,虽然这个操作过后它也可能就不是堆了,不过我们可以将首元素向下调整,让它成为堆。比刚才的方案效率要高得多。
比如我们删除大堆中的一个元素
调整过程:
调整后的结果:
代码示例:
void AdjustDOWN(HpDataType* arr, int size, int parent) {int child = parent * 2 + 1;while (child < size){if ((child+1)<size&&arr[child] < arr[child + 1])child++;if (arr[child] > arr[parent]){Swap(&arr[parent], &arr[child]);parent = child;child = parent * 2 + 1;}elsebreak;} }★如果是小堆只需要把if条件里兄弟节点的大小关系和父子节点的大小关系改变一下就行
4.源码:
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
void HeapInit(Heap* ps)//初始化
{assert(ps);ps->arr = NULL;ps->cap = ps->size = 0;
}
void HeapDestory(Heap* hp)//销毁堆
{assert(hp);free(hp->arr);hp->cap = hp->size = 0;
}
void Swap(HpDataType* a, HpDataType* b)//交换元素
{HpDataType c = *a;*a = *b;*b = c;
}
void AdjustUP(HpDataType* arr,int child)//向下调整
{int parent = (child - 1) / 2;while (child>0){if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}
void AdjustDOWN(HpDataType* arr, int size, int parent)//向上调整
{int child = parent * 2 + 1;while (child < size){if (arr[child] > arr[child + 1])child++;if ((child+1)<size&&arr[child] < arr[parent]){Swap(&arr[parent], &arr[child]);parent = child;child = parent * 2 + 1;}elsebreak;}
}
void HeapPush(Heap* ps, HPDataType x)//插入元素
{assert(ps);if (ps->size == ps->cap){int pnc = ps->cap == 0 ? 4 : 2 * ps->cap;HpDataType* pnew = realloc(ps->arr, sizeof(HPDataType)*pnc);assert(pnew);ps->arr = pnew;ps->cap = pnc;}ps->arr[ps->size] = x;ps->size++;AdjustUP(ps->arr, ps->size - 1);
}
void HeapPop(Heap* hp)//删除元素
{assert(hp);assert(hp->size);if (hp->size == 1){hp->size--;return;}Swap(&(hp->arr[0]), &(hp->arr[hp->size - 1]));hp->size--;AdjustDOWN(hp->arr, hp->size, 0);
}
HPDataType HeapTop(Heap* hp)//取堆顶元素
{assert(hp);assert(hp->size);return hp->arr[0];
}
int HeapSize(Heap* hp)//计算堆元素个数
{assert(hp);return hp->size;
}
int HeapEmpty(Heap* hp)//判断堆是否为空
{assert(hp);return hp->size == 0;
}三.建堆算法
在学习建堆算法的时候我们以对数组建堆为例,就是把数组的数据之间的关系做成一个堆结构,一般有两种方法,向上调整建堆和向下调整建堆,具体怎么做我们来看下面。
1.向上建堆法
向上建堆法也就是通过向上调整建堆,我们拿到一个数组后可以把数组的首元素当做堆,第二个元素当做把新的元素插入堆,然后通过向上调整构成新的堆,以此类推下去把数组遍历完后一个堆就建成了。时间复杂度为O(N*logN)
代码示例:
#include<stdio.h>
#include"Heap.h"
int main()
{int arr[] = { 1,9,3,7,6,4,2,10,8,5 };int size = sizeof(arr) / sizeof(int);for (int i = 0; i < size; i++)AdjustUP(arr, i);//该函数在上文已给出,这里不再展示printf("建大堆后:\n");for (int i = 0; i < size; i++)printf("%d ", arr[i]);return 0;
}不过该方法相比向下调整建堆效率比较低,我们来看向下调整建堆法。
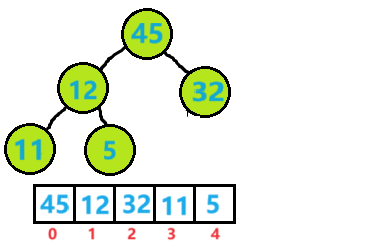
2.向下建堆法
向下建堆法也就是通过向下调整建堆,要注意并不是从首元素开始调整,因为刚开始它并不满足左右子树都是堆结构,所以不能直接从第一个元素开始向下调整。既然要满足左右子树都是堆那么我们可以考虑从最后一个元素开始调整,不过最后一层下面已经没有元素了,它已经是堆,并不用调整,那么我们从倒数第二层开始调整,所以我们先来计算一下倒数第二层最后一个父节点的下标:
(size-1-1)/2
第一个size-1得到二叉树的最后一个元素的下标,再减一除以二得到它的父节点的下标。
代码示例:
#include<stdio.h>
#include"Heap.h"
int main()
{int arr[] = { 1,9,3,7,6,4,2,10,8,5 };int size = sizeof(arr) / sizeof(int);for (int i = (size - 1 - 1) / 2; i >= 0; i--)AdjustDOWN(arr, size,i);//该函数在上文已给出,这里不再展示printf("建大堆后:\n");for (int i = 0; i < size; i++)printf("%d ", arr[i]);return 0;
}它的时间复杂度为O(N)证明如下:
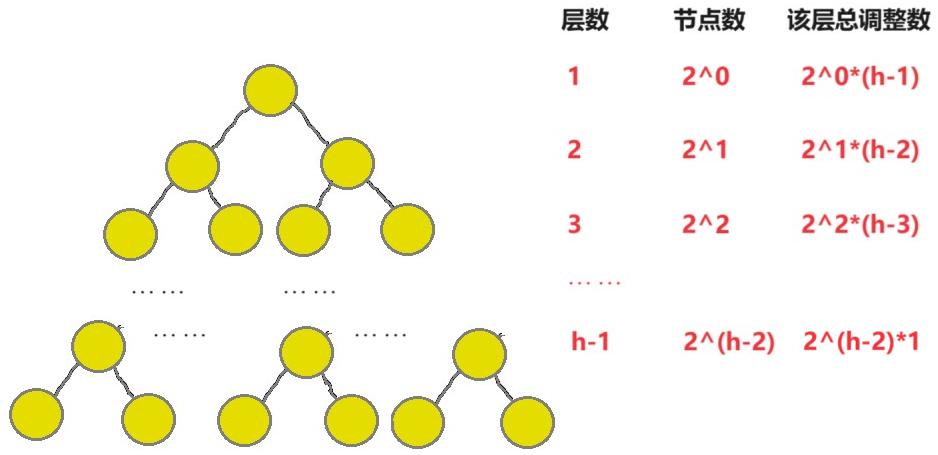
其中Sn为总的调整次数.

四.堆排序
给一个数组建堆后利用堆的性质给数组排序,使其效率更高,这就是一个堆排序。比如现在要对一个数组进行堆排序,第一个问题就是建大堆还是小堆,怎么利用堆来给数组排序。
要进行升序就需要建大堆,如果建的是小堆,那么堆顶也就是首元素就是最小的元素,并不需要动,那么来处理第二个元素就注意到它并不一定是第二小的元素,只能从第二个元素开始重新建一个小堆,那么每排一个元素都需要重新建一个小堆效率就会变得很低。
升序建大堆的话,第一个元素就是最大的元素,我们可以让它与最后一个元素互换,然后把堆的元素个数减一(就是把最后一个元素当做是堆外),最后把堆顶元素向下调整,反复操作直到堆的元素个数变为了零。这样一个数组就按升序排好了。
降序需要建小堆,原理和排升序相同这里就不在赘述。
代码示例:
#include<stdio.h>
#include"Heap.h"
int main()
{int arr[] = { 1,9,3,7,6,4,2,10,8,5 };int size = sizeof(arr) / sizeof(int);for (int i = (size - 1 - 1) / 2; i >= 0; i--)AdjustDOWN(arr, size,i);printf("建大堆后:\n");for (int i = 0; i < size; i++)printf("%d ", arr[i]);while (size){Swap(&arr[0], &arr[size - 1]);//交换元素size--;AdjustDOWN(arr, size, 0);}printf("\n排序后;\n");for (int i = 0; i < sizeof(arr) / sizeof(int); i++)printf("%d ", arr[i]);return 0;
}五.在文件中Top出最小的K个数
用堆结构的一个好处就在于,不需要排序就能高效的找出最小的前n个元素或最大的前n个元素,现在我们来利用堆来尝试找出文件中最小的K个数,一个比较低效的一个方法就是把文件中涉及到的所以数据都取出来然后把它建成一个小堆,然后Pop出前k次,得到最小的k个数。但是如果这个数据非常的大呢,比如有上亿个数据,那么就会消耗很大的内存空间。
有一个很优的方法就是只取出文件的前K个数建成一个大堆,也就是说这个堆只用储K个元素,那么堆顶就是这个堆的最大元素,然后继续遍历文件每遍历一个元素都与堆顶元素作比较,如果比堆顶元素小就更新一下堆顶元素(把小的那个变成堆顶元素),然后进行向下调整,直到遍历完整个文件,那么此时堆中的元素就是文件中最小的K个元素。此方法在时间复杂度上与上一方法差不多,但它大大的节省了空间。
代码示例:
#include<stdio.h>
#include"Heap.h"
void CreateNDate()
{//造数据,写入文件中int n = 10000;srand((unsigned int)time(NULL));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = rand() % 1000000;fprintf(fin, "%d\n", x);}fclose(fin);
}
void PrintTopK(int k)
{int* arr = (int*)malloc(sizeof(int) * k);assert(arr);FILE* fop = fopen("data.txt", "r");if (!fop){perror("fopen error");return;}for (int i = 0; i < k; i++)//先取出k个建大堆fscanf(fop, "%d", &arr[i]);for (int i = (k - 1 - 1) / 2; i >= 0; i--)AdjustDOWN(arr, k, i);int x = 0;while (fscanf(fop, "%d", &x) != EOF){if (arr[0] > x){arr[0] = x;AdjustDOWN(arr, k, 0);}}for (int i = 0; i < k; i++)//输出堆中元素printf("%d ", arr[i]);
}
int main()
{CreateNDate();int k = 0;scanf("%d", &k);PrintTopK(k);return 0;
}相关文章:

堆(建堆算法,堆排序)
目录 一.什么是堆? 1.堆 2.堆的储存 二.堆结构的创建 1.头文件的声明: 2.向上调整 3.向下调整 4.源码: 三.建堆算法 1.向上建堆法 2.向下建堆法 四.堆排序 五.在文件中Top出最小的K个数 一.什么是堆? 1.堆 堆就…...
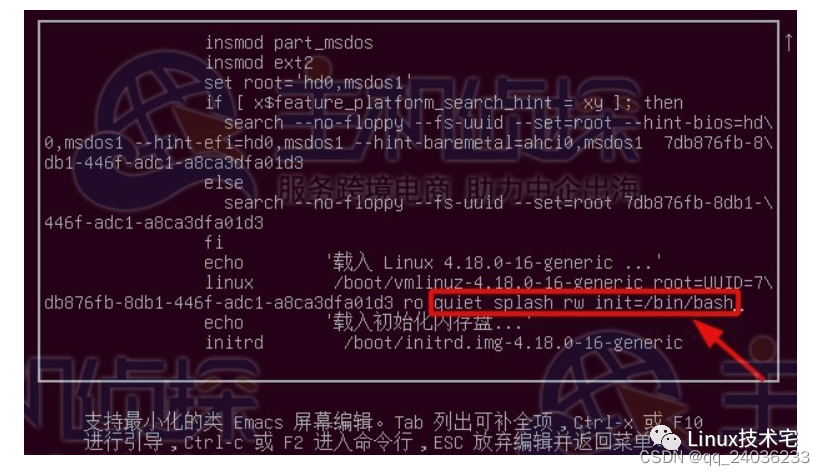
Linux内核重置root密码
Ubuntu 首先重新启动Ubuntu系统,然后快速按下shift键,以调出grub启动菜单在这里我们选择第二个(Ubuntu高级选项),选中后按下Enter键 选择最高的Linux内核版本所对应的recovery mode模式,按e键编辑启动项 在…...
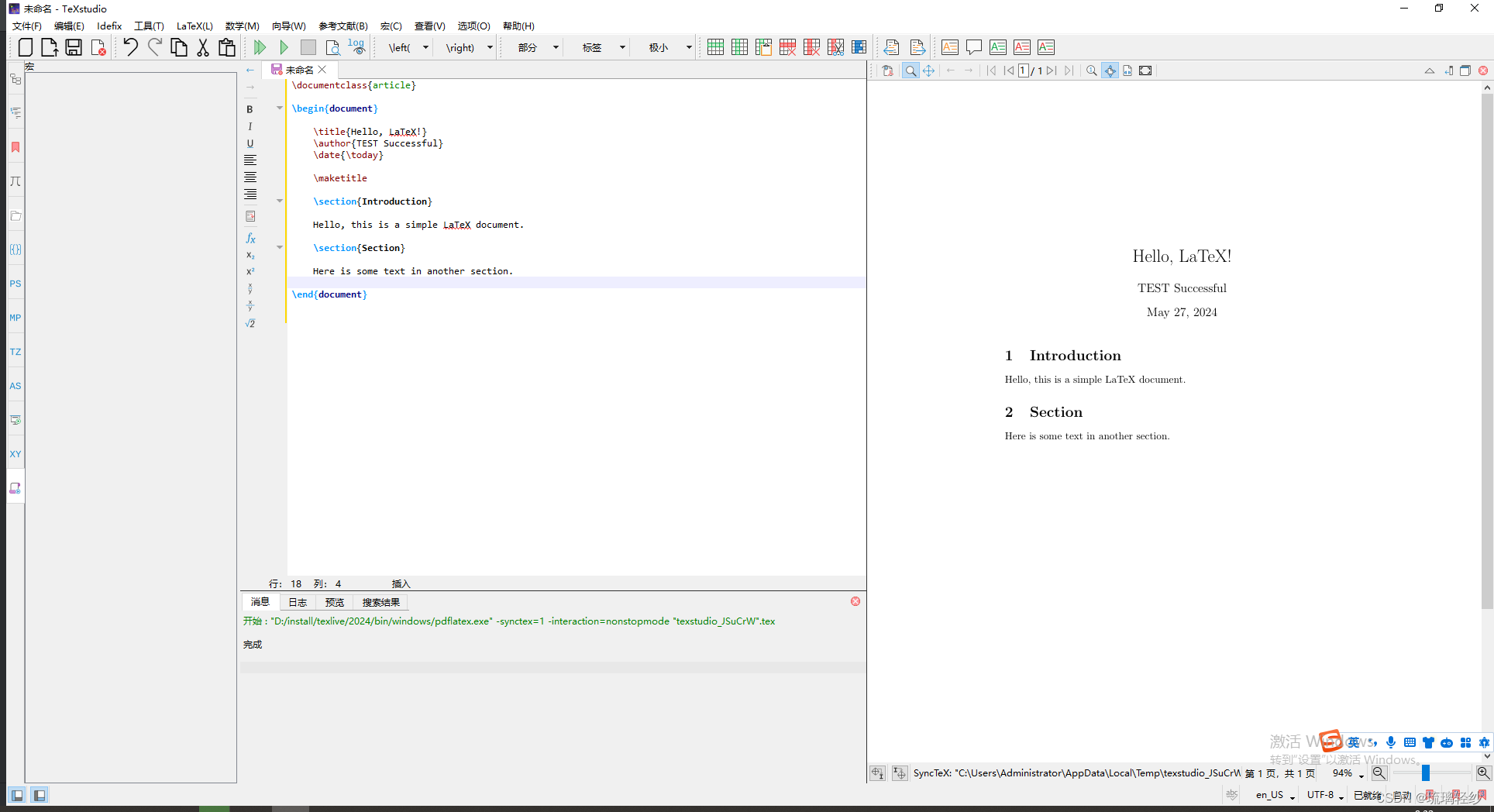
LaTex安装及配置(Windows)
LaTex安装及配置(Windows) 安装环境安装texlive下载texlive安装 编辑器安装texstudio下载texstudio安装 环境配置 使用第一个LaTex文档新建文件编程查看results 安装 环境安装 texlive下载 镜像清华源下载地址:https://mirrors.tuna.tsing…...
这才是满分毕业答辩PPT!
这才是满分毕业答辩PPT! 2024年 毕业答辩论文指南 创新 正式 高效 正值毕业季,是不是很多同学,非常头疼如何进行论文答辩? 要想导师满意,顺利毕业,那么手里必须有份优秀的答辩PPT。这将是你的秘密武器&…...

【字典树(前缀树) 字符串】2416. 字符串的前缀分数和
本文涉及知识点 字典树(前缀树) 字符串 LeetCode 2416. 字符串的前缀分数和 给你一个长度为 n 的数组 words ,该数组由 非空 字符串组成。 定义字符串 word 的 分数 等于以 word 作为 前缀 的 words[i] 的数目。 例如,如果 words [“a”,…...

X-CSV-Reader:一个使用Rust实现CSV命令行读取器
🎈效果演示 ⚡️快速上手 依赖导入: cargo add csv读取实现: use std::error::Error; use std::fs::File; use std::path::Path;fn read_csv<P: AsRef<Path>>(filename: P) -> Result<(), Box<dyn Error>> {le…...

集成ECharts到若依框架:原理与使用方法详解
ECharts 是一个强大的开源数据可视化库,基于 JavaScript,能够创建丰富多彩的图表和交互数据展示。结合若依框架(RuoYi),我们可以非常方便地将 ECharts 集成到系统中,实现数据的可视化展示。本文将详细介绍 …...
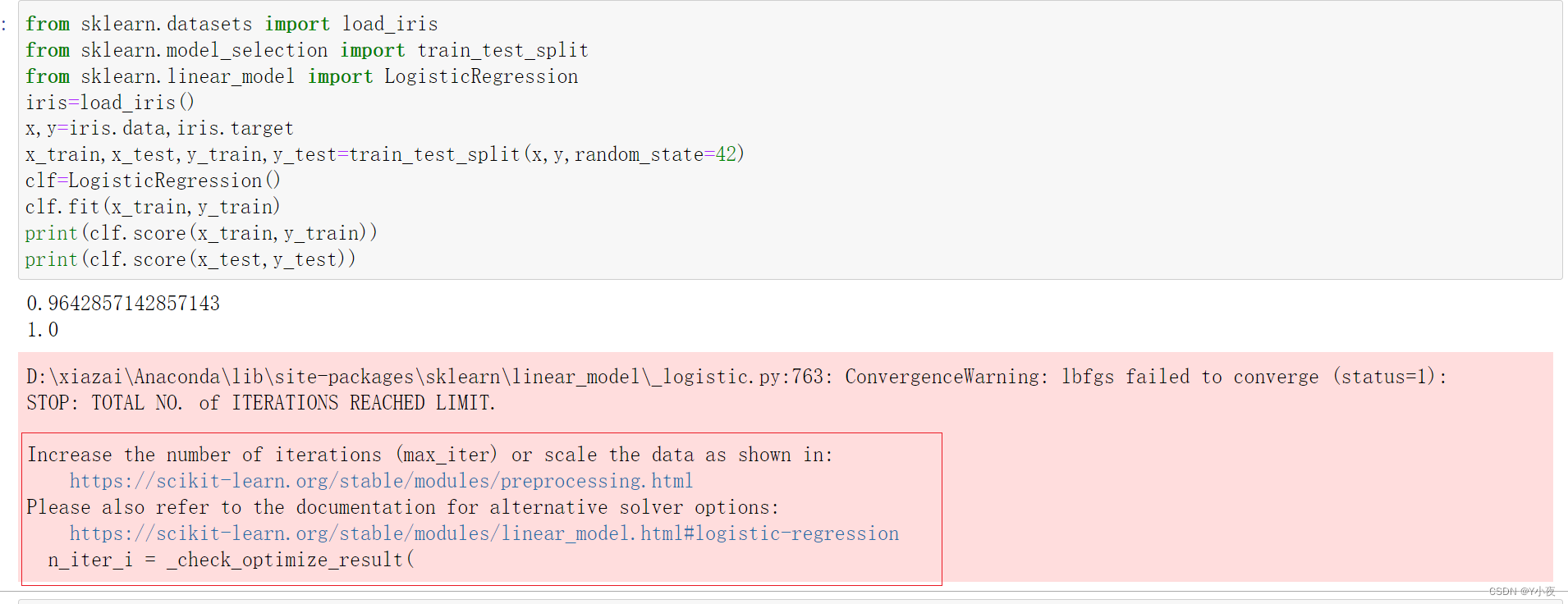
【机器学习】——线性模型
💻博主现有专栏: C51单片机(STC89C516),c语言,c,离散数学,算法设计与分析,数据结构,Python,Java基础,MySQL,linux…...

最全的Redis常用命令
Redis是一个开源的内存数据结构存储系统,用作数据库、缓存和消息代理。它支持多种类型的数据结构,如字符串(strings)、哈希(hashes)、列表(lists)、集合(sets)…...
sourcetree推送到git上面
官网:Sourcetree | Free Git GUI for Mac and Windows 下载到1次提交 下载后打开 点击跳过 下一步 名字邮箱 点击clone 把自己要上传的代码粘贴到里面去 返回点击远程->点击暂存所有 加载完毕后,输入提交内容提交 提交完成了 2次提交 把文件夹内的…...

勒索病毒的策略与建议
随着网络技术的快速发展,勒索病毒攻击成为全球范围内日益严重的网络安全威胁。勒索病毒通过加密用户文件或锁定系统来勒索赎金,给个人和企业带来了巨大的损失。因此,了解如何应对勒索病毒攻击至关重要。本文将概述一些有效的防范措施和应对策…...
——输出格式)
doxygen 1.11.0 使用详解(十四)——输出格式
目录 HTMLLATEXMan pagesRTFXMLDocBookCompiled HTML Help (a.k.a. Windows 98 help)Qt Compressed Help (.qch)Eclipse HelpXCode DocSetsPostScriptPDF The following output formats are directly supported by doxygen: HTML Generated if GENERATE_HTML is set to YES i…...

java list<AnalystEducationDO> 转成List<AnalystEducationRespVO>两个对象的属性一样
如果AnalystEducationDO和AnalystEducationRespVO两个类的属性完全相同,且遵循Java Bean的命名规范(即具有相应的getter和setter方法),你可以利用一些库来简化转换过程,比如Apache BeanUtils或Spring Framework的BeanU…...
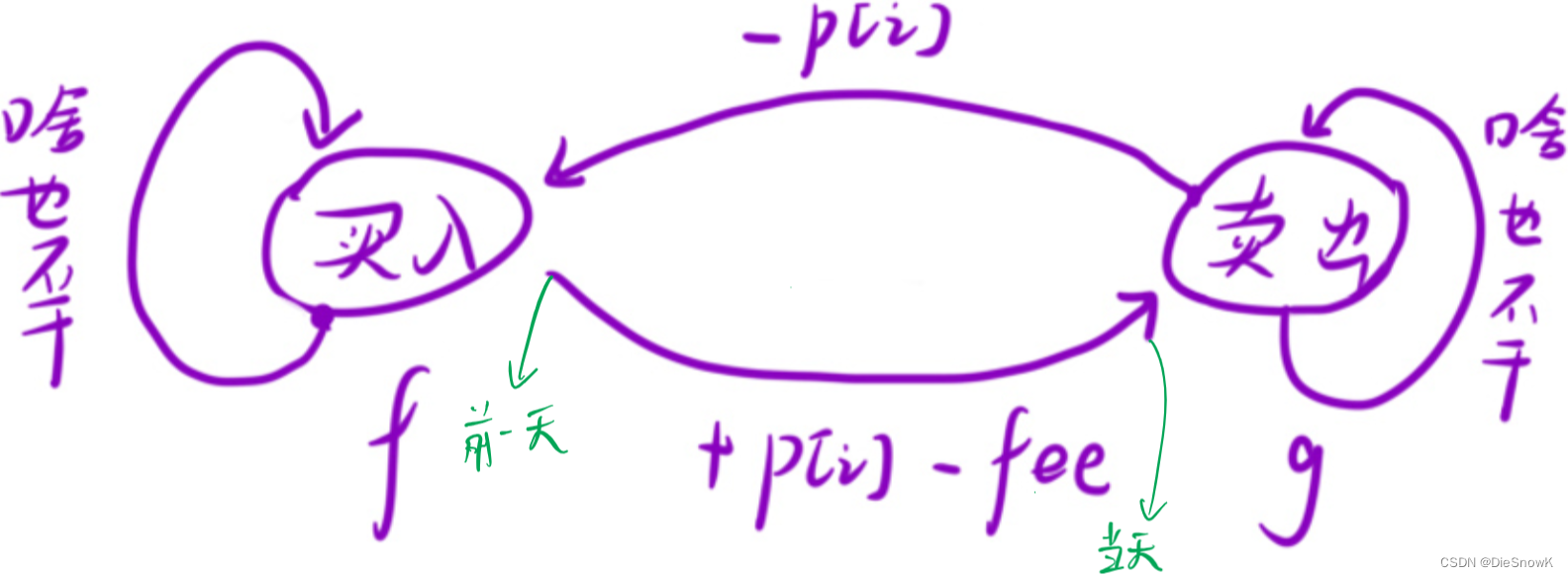
[Algorihm][简单多状态DP问题][买卖股票的最佳时机含冷冻期][买卖股票的最佳时机含手续费]详细讲解
目录 1.买卖股票的最佳时机含冷冻期1.题目链接买卖股票的最佳时机含冷冻期2.算法原理详解3.代码实现 2.买卖股票的最佳时机含手续费1.题目链接2.算法原理详解3.代码实现 1.买卖股票的最佳时机含冷冻期 1.题目链接 买卖股票的最佳时机含冷冻期 2.算法原理详解 思路ÿ…...
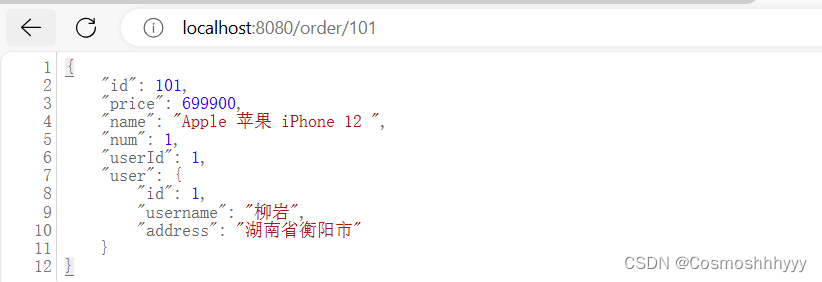
微服务:利用RestTemplate实现远程调用
打算系统学习一下微服务知识,从今天开始记录。 远程调用 调用order接口,查询。 由于实现还未封装用户信息,所以为null。 下面我们来使用远程调用用户服务的接口,然后封装一下用户信息返回即可。 流程图 配置类中注入RestTe…...
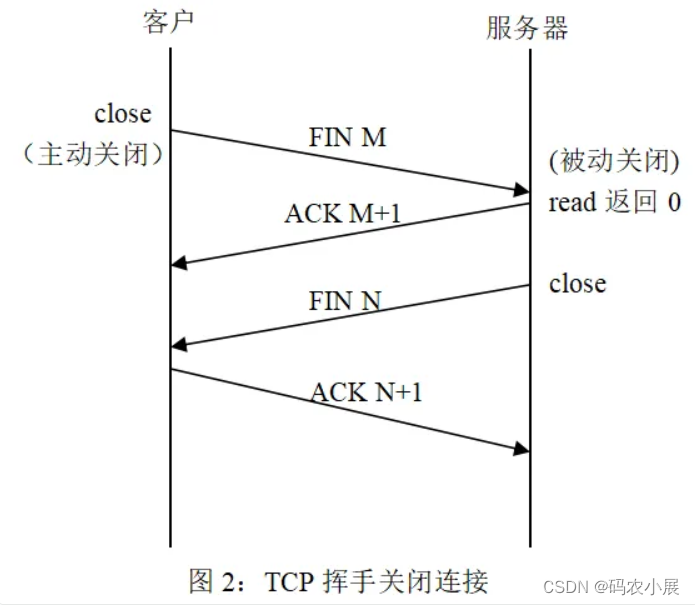
【Linux】TCP的三次握手和四次挥手
三次握手 在TCP/IP协议中,TCP协议提供可靠的连接服务,采用三次握手建立一个连接。注意!三次握手只是用来建立连接用的,和TCP可靠稳定没有关系,TCP的可靠是通过重传和检错等机制实现的。 默认创建一个socket后ÿ…...
爬山算法全解析:掌握优化技巧,攀登技术高峰!
一、引言 爬山算法是一种局部搜索算法,它基于当前解的邻域中进行搜索,通过比较当前解与邻域解的优劣来更新当前解,从而逐步逼近最优解。本文将对爬山算法进行详细的介绍。 二、爬山算法简介 爬山算法是一种基于贪心策略的优化算法ÿ…...
使用 Ollama框架 下载和使用 Llama3 AI大模型的完整指南
🏡作者主页:点击! 🤖AI大模型部署与应用专栏:点击! ⏰️创作时间:2024年5月24日20点59分 🀄️文章质量:96分 目录 💥Ollama介绍 主要特点 主要优点 应…...
最新流媒体在线音乐系统网站源码| 音乐社区 | 多语言 | 开心版
最新流媒体在线音乐系统网站源码 源码免费下载地址抄笔记 (chaobiji.cn)...
中国改革报是什么级别的报刊?在哪些领域具有较高的影响力?
中国改革报是什么级别的报刊?在哪些领域具有较高的影响力? 《中国改革报》是国家发展和改革委员会主管的全国性综合类报纸。它在经济领域和改革发展方面具有重要的影响力,是传递国家政策、反映改革动态的重要平台。该报对于推动中国的经济改…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...