LeetCode 279 —— 完全平方数
阅读目录
- 1. 题目
- 2. 解题思路
- 3. 代码实现
1. 题目

2. 解题思路
此图利用动态规划进行求解,首先,我们求出小于 n n n 的所有完全平方数,存放在数组 squareNums 中。
定义 dp[n] 为和为 n n n 的完全平方数的最小数量,那么有状态转移方程:
d p [ n ] = m i n ( d p [ n − s q u a r e N u m s [ i ] ] + 1 , d p [ n ] ) , 对于任意 s q u a r e N u m s [ i ] < n dp[n] = min(dp[n-squareNums[i]] + 1, dp[n]), 对于任意 \space squareNums[i] < n dp[n]=min(dp[n−squareNums[i]]+1,dp[n]),对于任意 squareNums[i]<n
d p [ n ] = 1 ,对于 s q u a r e N u m s [ i ] = = n dp[n] = 1,对于 \space squareNums[i] == n dp[n]=1,对于 squareNums[i]==n
3. 代码实现
class Solution {
public:int numSquares(int n) {vector<int> squareNums;for (int i = 1; i < n; ++i) {if (i * i > n) {break;}squareNums.push_back(i * i);}vector<int> dp(n+1, 10000);dp[1] = 1;for (int i = 2; i <= n; ++i) {for (int j = 0; j < squareNums.size(); ++j) {if (squareNums[j] > i) {break;} else if (squareNums[j] == i) {dp[i] = 1;} else {dp[i] = min(dp[i], dp[i - squareNums[j]] + 1);} }}return dp[n];}
};
时间复杂度为 O ( n n ) O(n\sqrt{n}) O(nn),第一层循环 n n n 次,第二层循环 n \sqrt{n} n 次,空间复杂度为 O ( n ) O(n) O(n),其中 squareNums 占用空间为 O ( n ) O(\sqrt{n}) O(n),也可以省略,直接在第二个循环得到 j ∗ j j*j j∗j,dp 占用空间为 O ( n ) O(n) O(n)。
相关文章:

LeetCode 279 —— 完全平方数
阅读目录 1. 题目2. 解题思路3. 代码实现 1. 题目 2. 解题思路 此图利用动态规划进行求解,首先,我们求出小于 n n n 的所有完全平方数,存放在数组 squareNums 中。 定义 dp[n] 为和为 n n n 的完全平方数的最小数量,那么有状态…...

PHP发票真假API、医疗电子票据查验、发票识别接口开发示例
“营”“增”两种税是主流的流转税种,是两个独立而不能交叉的税种。也就是说交增值税的话就不交营业税,而交了营业税就不需要交增值税。而且,两者在征收的对象、征税范围、计税的依据、税目、税率以及征收管理等都有所不同,增值税…...

Python库之`lxml`的高级用法深度解析
Python库之lxml的高级用法深度解析 简介 lxml是一个功能强大的第三方库,它提供了对XML和HTML文档的高效处理能力。除了基本的解析和创建功能外,lxml还包含了一些高级用法,这些用法可以帮助开发者在处理复杂文档时更加得心应手。 高级解析技…...

参数的本质:详解 JavaScript 函数的参数
文章导读:AI 辅助学习前端,包含入门、进阶、高级部分前端系列内容,当前是 JavaScript 的部分,瑶琴会持续更新,适合零基础的朋友,已有前端工作经验的可以不看,也可以当作基础知识回顾。 上篇文章…...

悲痛都会过去,唯有当下值得珍惜
在生活的长河中,我们都会经历各种各样的悲痛与挫折,无论是来自原生家庭的困扰,婚姻中的曲折,还是小时候的创伤、男女关系中的纠葛、校园时期的霸凌。然而,当我们回首过去,曾经以为无法逾越的痛苦࿰…...

第三方软件测试机构进行代码审计需要哪些专业的知识?
代码审计 进行代码审计需要专业的知识,包括编程语言、操作系统、数据库、网络知识以及安全知识等。 1.编程语言知识是进行代码审计的基础,因为你需要理解代码的语法和结构。对于不同的应用程序,你需要了解其所使用的编程语言的特点和语法规…...
Modal.method() 不显示头部的问题
ant-design中的Modal组件有两种用法: 第一种是用标签:<a-modal></a-modal> 第二种是用Api:Modal.info、Modal.warning、Modal.confirm...... 一开始项目中这两种用法是混用的,后面UI改造,需要统一样式&…...

Java中的内部类及其用途
一、技术难点 在Java中,内部类是一个定义在另一个类内部的类。这种嵌套的结构带来了一些技术上的难点和挑战: 访问控制:内部类可以直接访问外部类的所有成员(包括私有成员),但外部类不能直接访问内部类的…...

堆(建堆算法,堆排序)
目录 一.什么是堆? 1.堆 2.堆的储存 二.堆结构的创建 1.头文件的声明: 2.向上调整 3.向下调整 4.源码: 三.建堆算法 1.向上建堆法 2.向下建堆法 四.堆排序 五.在文件中Top出最小的K个数 一.什么是堆? 1.堆 堆就…...
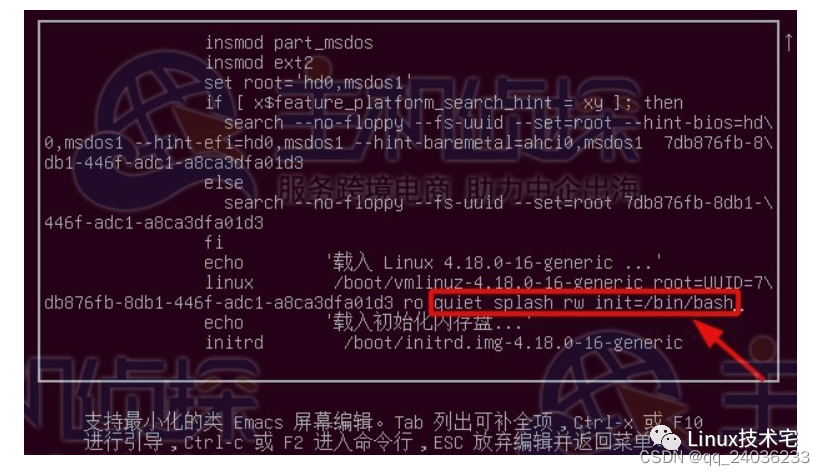
Linux内核重置root密码
Ubuntu 首先重新启动Ubuntu系统,然后快速按下shift键,以调出grub启动菜单在这里我们选择第二个(Ubuntu高级选项),选中后按下Enter键 选择最高的Linux内核版本所对应的recovery mode模式,按e键编辑启动项 在…...
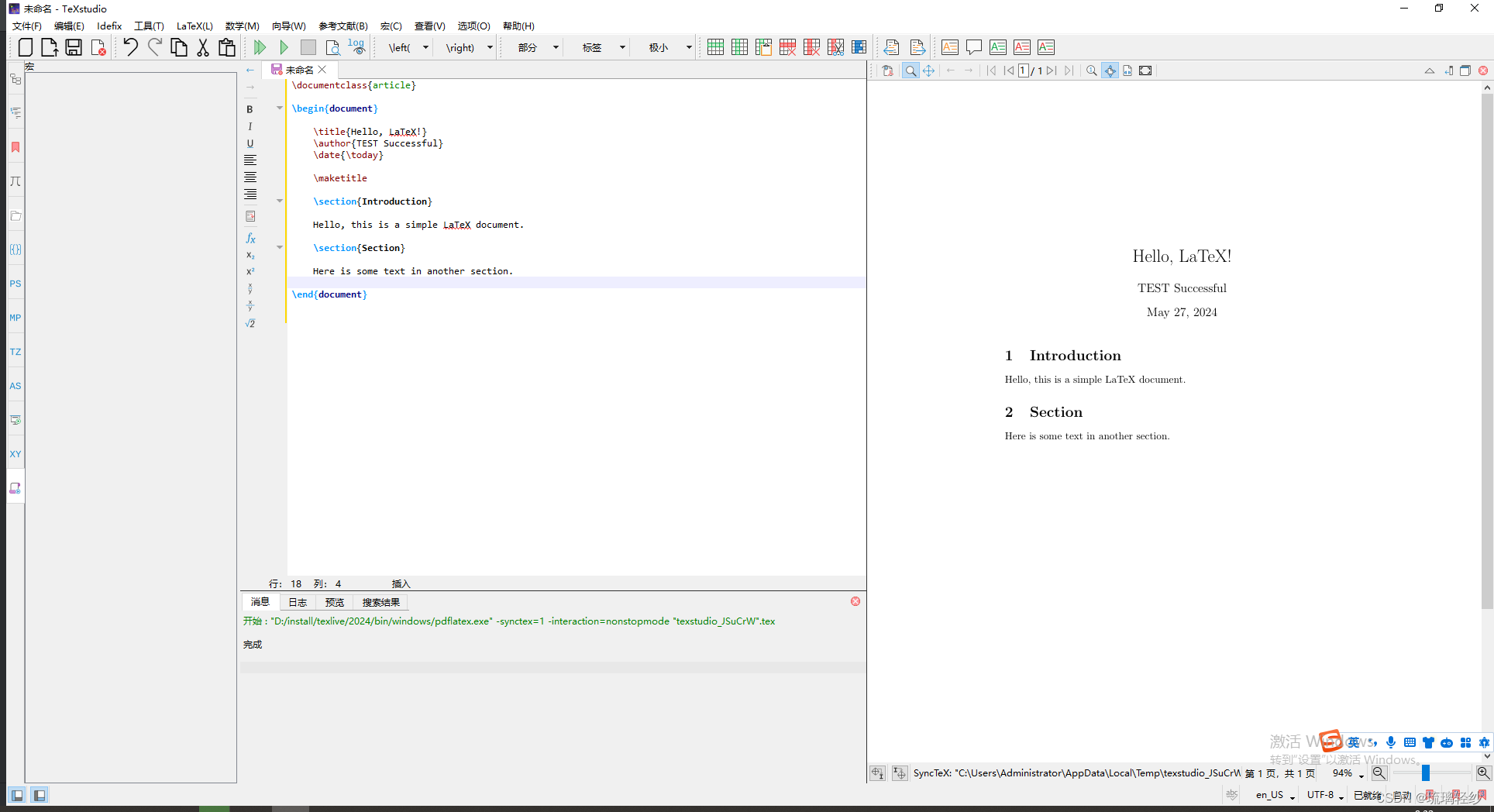
LaTex安装及配置(Windows)
LaTex安装及配置(Windows) 安装环境安装texlive下载texlive安装 编辑器安装texstudio下载texstudio安装 环境配置 使用第一个LaTex文档新建文件编程查看results 安装 环境安装 texlive下载 镜像清华源下载地址:https://mirrors.tuna.tsing…...
这才是满分毕业答辩PPT!
这才是满分毕业答辩PPT! 2024年 毕业答辩论文指南 创新 正式 高效 正值毕业季,是不是很多同学,非常头疼如何进行论文答辩? 要想导师满意,顺利毕业,那么手里必须有份优秀的答辩PPT。这将是你的秘密武器&…...

【字典树(前缀树) 字符串】2416. 字符串的前缀分数和
本文涉及知识点 字典树(前缀树) 字符串 LeetCode 2416. 字符串的前缀分数和 给你一个长度为 n 的数组 words ,该数组由 非空 字符串组成。 定义字符串 word 的 分数 等于以 word 作为 前缀 的 words[i] 的数目。 例如,如果 words [“a”,…...

X-CSV-Reader:一个使用Rust实现CSV命令行读取器
🎈效果演示 ⚡️快速上手 依赖导入: cargo add csv读取实现: use std::error::Error; use std::fs::File; use std::path::Path;fn read_csv<P: AsRef<Path>>(filename: P) -> Result<(), Box<dyn Error>> {le…...

集成ECharts到若依框架:原理与使用方法详解
ECharts 是一个强大的开源数据可视化库,基于 JavaScript,能够创建丰富多彩的图表和交互数据展示。结合若依框架(RuoYi),我们可以非常方便地将 ECharts 集成到系统中,实现数据的可视化展示。本文将详细介绍 …...
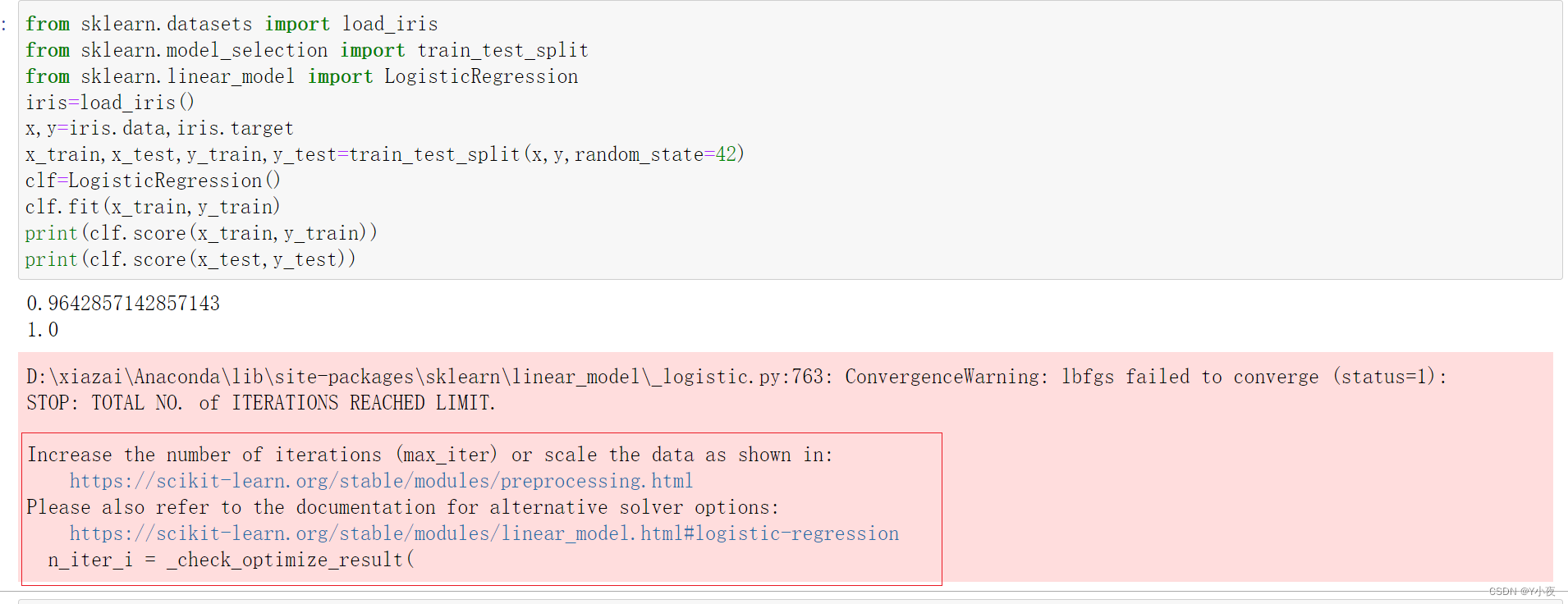
【机器学习】——线性模型
💻博主现有专栏: C51单片机(STC89C516),c语言,c,离散数学,算法设计与分析,数据结构,Python,Java基础,MySQL,linux…...

最全的Redis常用命令
Redis是一个开源的内存数据结构存储系统,用作数据库、缓存和消息代理。它支持多种类型的数据结构,如字符串(strings)、哈希(hashes)、列表(lists)、集合(sets)…...
sourcetree推送到git上面
官网:Sourcetree | Free Git GUI for Mac and Windows 下载到1次提交 下载后打开 点击跳过 下一步 名字邮箱 点击clone 把自己要上传的代码粘贴到里面去 返回点击远程->点击暂存所有 加载完毕后,输入提交内容提交 提交完成了 2次提交 把文件夹内的…...

勒索病毒的策略与建议
随着网络技术的快速发展,勒索病毒攻击成为全球范围内日益严重的网络安全威胁。勒索病毒通过加密用户文件或锁定系统来勒索赎金,给个人和企业带来了巨大的损失。因此,了解如何应对勒索病毒攻击至关重要。本文将概述一些有效的防范措施和应对策…...
——输出格式)
doxygen 1.11.0 使用详解(十四)——输出格式
目录 HTMLLATEXMan pagesRTFXMLDocBookCompiled HTML Help (a.k.a. Windows 98 help)Qt Compressed Help (.qch)Eclipse HelpXCode DocSetsPostScriptPDF The following output formats are directly supported by doxygen: HTML Generated if GENERATE_HTML is set to YES i…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
