Java中的内部类及其用途
一、技术难点
在Java中,内部类是一个定义在另一个类内部的类。这种嵌套的结构带来了一些技术上的难点和挑战:
- 访问控制:内部类可以直接访问外部类的所有成员(包括私有成员),但外部类不能直接访问内部类的私有成员。这要求开发者在设计内部类时,需要仔细考虑访问权限和数据封装的问题。
- 命名冲突:如果内部类与外部类的成员具有相同的名称,那么内部类的名称将覆盖外部类的成员名称。这可能导致代码的可读性和可维护性降低。
- 内存管理:由于内部类对象与外部类对象之间存在隐式的关联,因此内部类对象的生命周期可能会受到外部类对象的影响。这要求开发者在编写代码时,需要特别注意内存泄漏和对象生命周期的问题。
二、面试官关注点
在面试过程中,面试官可能会关注以下几个方面:
- 对内部类基本概念的理解:面试者是否能够清晰地解释什么是内部类,以及它与普通类的区别。
- 内部类的用途:面试者是否能够列举出内部类的主要用途,并解释其背后的原理。
- 技术难点:面试者是否了解内部类在访问控制、命名冲突和内存管理等方面的技术难点,并能够提出相应的解决方案。
- 代码示例:面试者是否能够提供具体的代码示例来演示内部类的使用方法和效果。
三、回答吸引力
在回答关于内部类的问题时,可以通过以下几个方面来增强回答的吸引力:
- 结构化表达:将回答内容组织成清晰的逻辑结构,先介绍基本概念,再列举用途,然后分析技术难点,最后提供代码示例。
- 深入剖析:对于每个用途和技术难点,都进行深入的分析和解释,让面试官感受到你对问题的深刻理解和全面把握。
- 举例说明:通过具体的代码示例来演示内部类的使用方法和效果,让面试官能够直观地感受到内部类的强大功能和灵活性。
四、代码举例
以下是一个简单的Java代码示例,演示了内部类的使用方法和效果:
java
public class OuterClass { |
private int outerVariable = 100; |
public class InnerClass { |
private int innerVariable = 200; |
public void displayVariables() { |
System.out.println("Outer variable: " + outerVariable); |
System.out.println("Inner variable: " + innerVariable); |
} |
} |
public InnerClass getInnerClassInstance() { |
return new InnerClass(); |
} |
public static void main(String[] args) { |
OuterClass outer = new OuterClass(); |
OuterClass.InnerClass inner = outer.getInnerClassInstance(); |
inner.displayVariables(); |
} |
} |
在这个示例中,我们定义了一个名为OuterClass的外部类和一个名为InnerClass的内部类。InnerClass可以直接访问OuterClass的私有成员outerVariable,并通过displayVariables()方法打印出两个变量的值。在main()方法中,我们通过OuterClass的实例来获取InnerClass的实例,并调用其displayVariables()方法来演示内部类的使用方法。
相关文章:

Java中的内部类及其用途
一、技术难点 在Java中,内部类是一个定义在另一个类内部的类。这种嵌套的结构带来了一些技术上的难点和挑战: 访问控制:内部类可以直接访问外部类的所有成员(包括私有成员),但外部类不能直接访问内部类的…...

堆(建堆算法,堆排序)
目录 一.什么是堆? 1.堆 2.堆的储存 二.堆结构的创建 1.头文件的声明: 2.向上调整 3.向下调整 4.源码: 三.建堆算法 1.向上建堆法 2.向下建堆法 四.堆排序 五.在文件中Top出最小的K个数 一.什么是堆? 1.堆 堆就…...
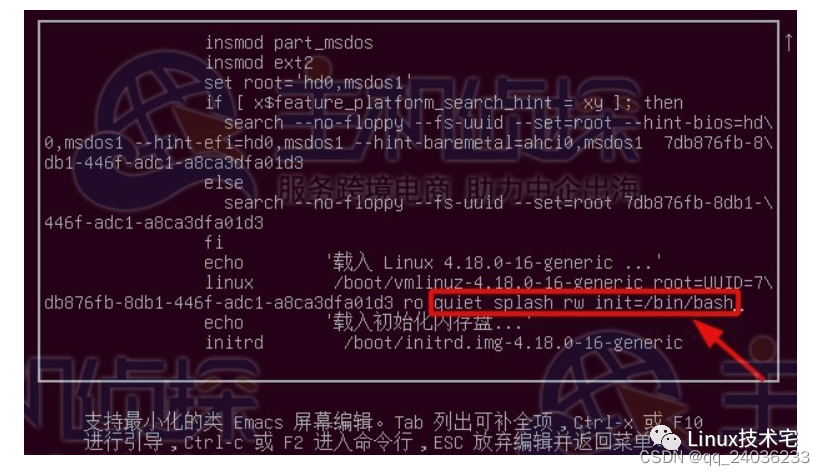
Linux内核重置root密码
Ubuntu 首先重新启动Ubuntu系统,然后快速按下shift键,以调出grub启动菜单在这里我们选择第二个(Ubuntu高级选项),选中后按下Enter键 选择最高的Linux内核版本所对应的recovery mode模式,按e键编辑启动项 在…...
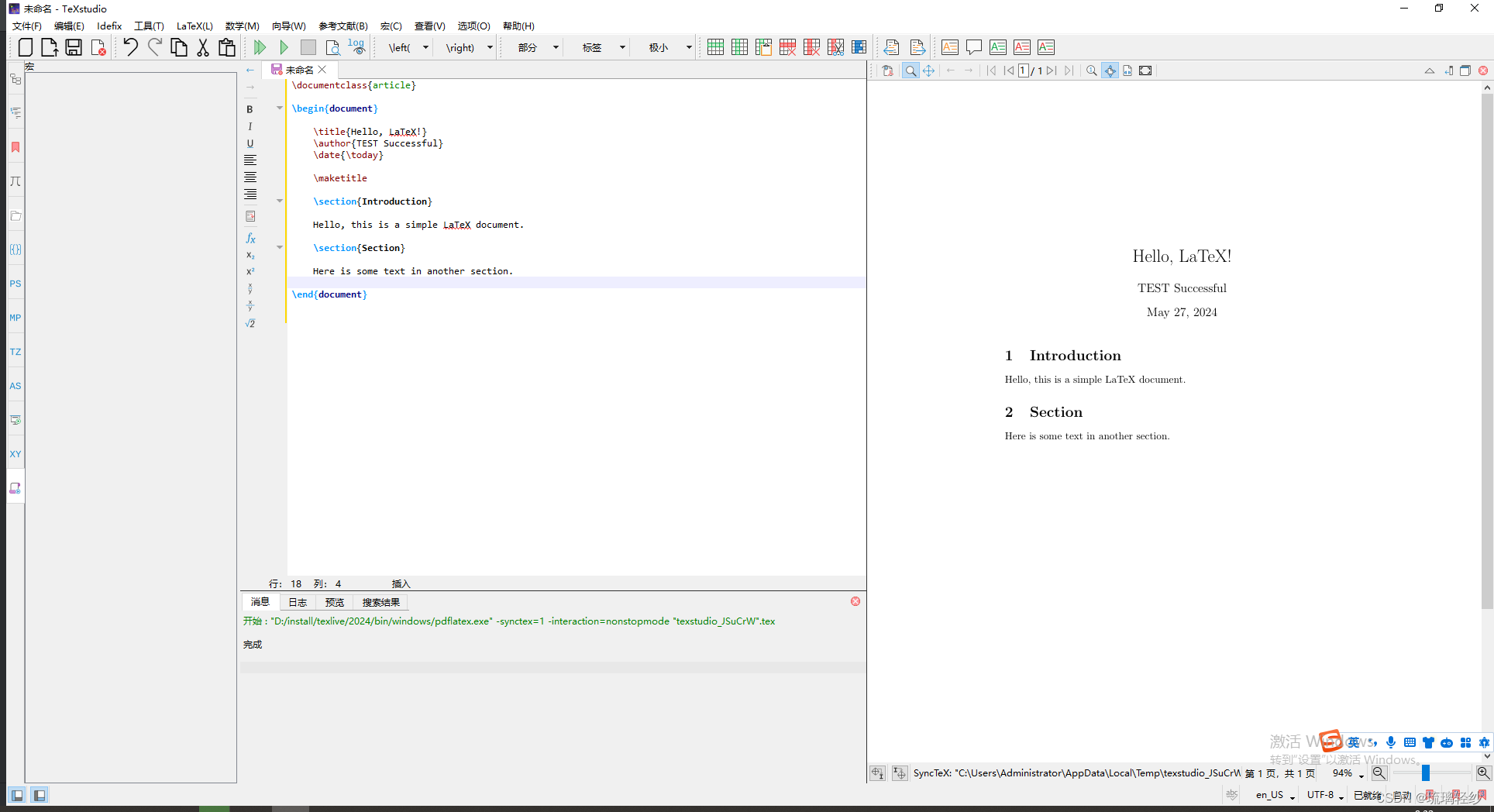
LaTex安装及配置(Windows)
LaTex安装及配置(Windows) 安装环境安装texlive下载texlive安装 编辑器安装texstudio下载texstudio安装 环境配置 使用第一个LaTex文档新建文件编程查看results 安装 环境安装 texlive下载 镜像清华源下载地址:https://mirrors.tuna.tsing…...
这才是满分毕业答辩PPT!
这才是满分毕业答辩PPT! 2024年 毕业答辩论文指南 创新 正式 高效 正值毕业季,是不是很多同学,非常头疼如何进行论文答辩? 要想导师满意,顺利毕业,那么手里必须有份优秀的答辩PPT。这将是你的秘密武器&…...

【字典树(前缀树) 字符串】2416. 字符串的前缀分数和
本文涉及知识点 字典树(前缀树) 字符串 LeetCode 2416. 字符串的前缀分数和 给你一个长度为 n 的数组 words ,该数组由 非空 字符串组成。 定义字符串 word 的 分数 等于以 word 作为 前缀 的 words[i] 的数目。 例如,如果 words [“a”,…...

X-CSV-Reader:一个使用Rust实现CSV命令行读取器
🎈效果演示 ⚡️快速上手 依赖导入: cargo add csv读取实现: use std::error::Error; use std::fs::File; use std::path::Path;fn read_csv<P: AsRef<Path>>(filename: P) -> Result<(), Box<dyn Error>> {le…...

集成ECharts到若依框架:原理与使用方法详解
ECharts 是一个强大的开源数据可视化库,基于 JavaScript,能够创建丰富多彩的图表和交互数据展示。结合若依框架(RuoYi),我们可以非常方便地将 ECharts 集成到系统中,实现数据的可视化展示。本文将详细介绍 …...
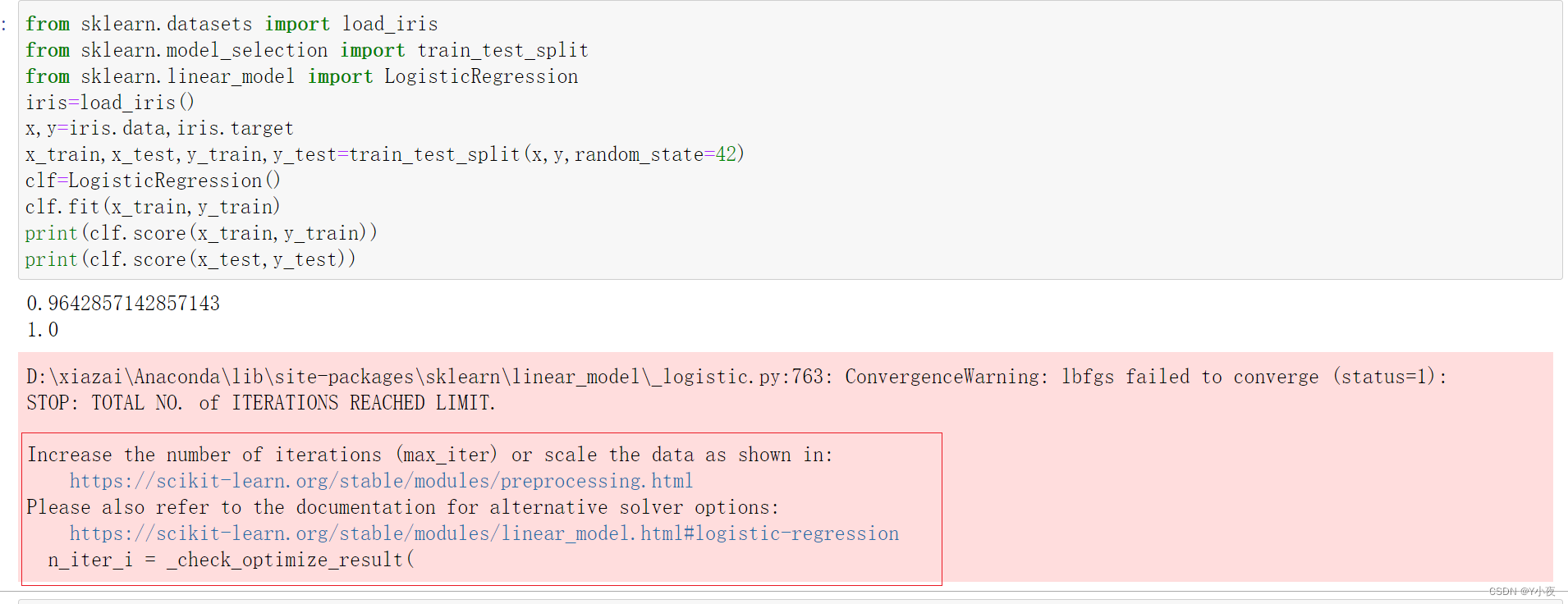
【机器学习】——线性模型
💻博主现有专栏: C51单片机(STC89C516),c语言,c,离散数学,算法设计与分析,数据结构,Python,Java基础,MySQL,linux…...

最全的Redis常用命令
Redis是一个开源的内存数据结构存储系统,用作数据库、缓存和消息代理。它支持多种类型的数据结构,如字符串(strings)、哈希(hashes)、列表(lists)、集合(sets)…...
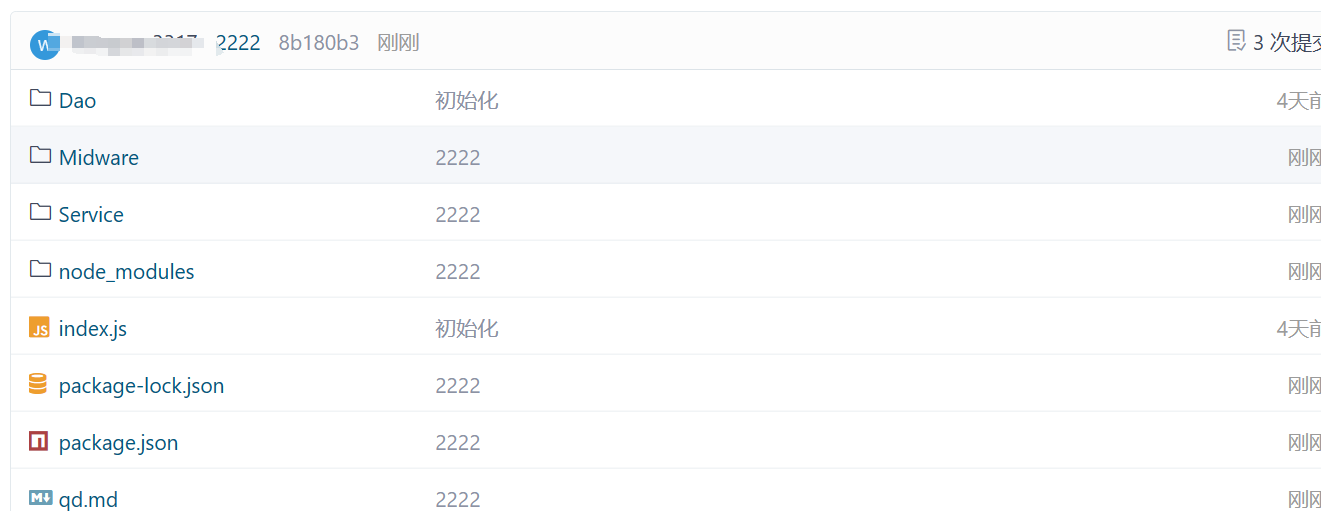
sourcetree推送到git上面
官网:Sourcetree | Free Git GUI for Mac and Windows 下载到1次提交 下载后打开 点击跳过 下一步 名字邮箱 点击clone 把自己要上传的代码粘贴到里面去 返回点击远程->点击暂存所有 加载完毕后,输入提交内容提交 提交完成了 2次提交 把文件夹内的…...

勒索病毒的策略与建议
随着网络技术的快速发展,勒索病毒攻击成为全球范围内日益严重的网络安全威胁。勒索病毒通过加密用户文件或锁定系统来勒索赎金,给个人和企业带来了巨大的损失。因此,了解如何应对勒索病毒攻击至关重要。本文将概述一些有效的防范措施和应对策…...
——输出格式)
doxygen 1.11.0 使用详解(十四)——输出格式
目录 HTMLLATEXMan pagesRTFXMLDocBookCompiled HTML Help (a.k.a. Windows 98 help)Qt Compressed Help (.qch)Eclipse HelpXCode DocSetsPostScriptPDF The following output formats are directly supported by doxygen: HTML Generated if GENERATE_HTML is set to YES i…...

java list<AnalystEducationDO> 转成List<AnalystEducationRespVO>两个对象的属性一样
如果AnalystEducationDO和AnalystEducationRespVO两个类的属性完全相同,且遵循Java Bean的命名规范(即具有相应的getter和setter方法),你可以利用一些库来简化转换过程,比如Apache BeanUtils或Spring Framework的BeanU…...
[Algorihm][简单多状态DP问题][买卖股票的最佳时机含冷冻期][买卖股票的最佳时机含手续费]详细讲解
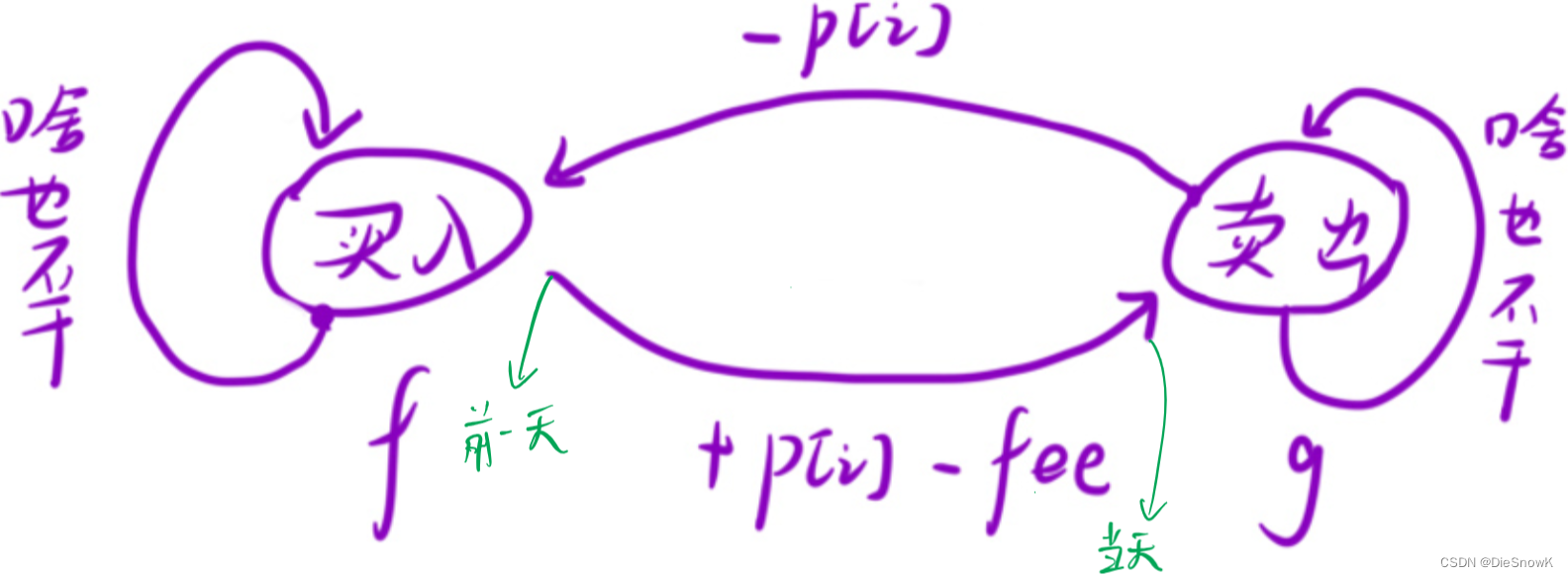
目录 1.买卖股票的最佳时机含冷冻期1.题目链接买卖股票的最佳时机含冷冻期2.算法原理详解3.代码实现 2.买卖股票的最佳时机含手续费1.题目链接2.算法原理详解3.代码实现 1.买卖股票的最佳时机含冷冻期 1.题目链接 买卖股票的最佳时机含冷冻期 2.算法原理详解 思路ÿ…...
微服务:利用RestTemplate实现远程调用
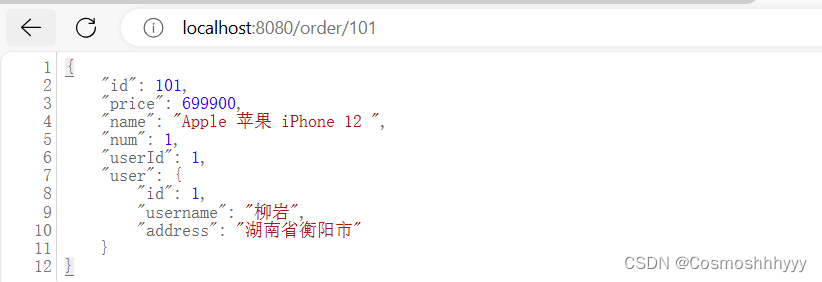
打算系统学习一下微服务知识,从今天开始记录。 远程调用 调用order接口,查询。 由于实现还未封装用户信息,所以为null。 下面我们来使用远程调用用户服务的接口,然后封装一下用户信息返回即可。 流程图 配置类中注入RestTe…...
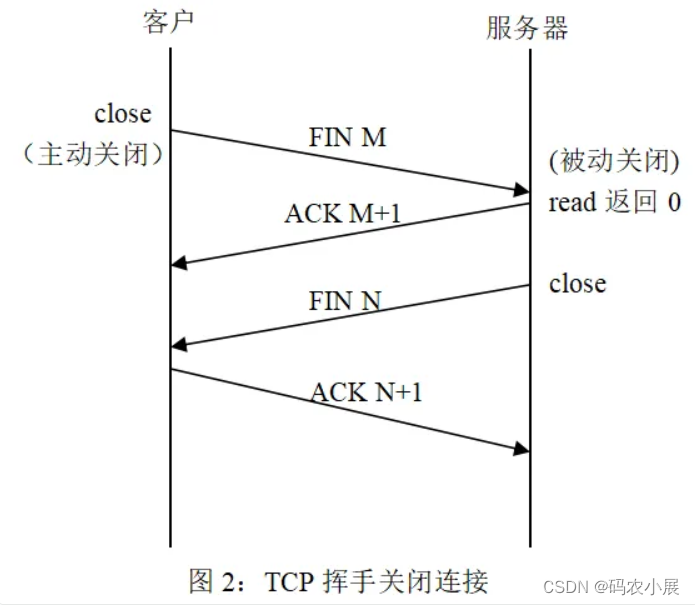
【Linux】TCP的三次握手和四次挥手
三次握手 在TCP/IP协议中,TCP协议提供可靠的连接服务,采用三次握手建立一个连接。注意!三次握手只是用来建立连接用的,和TCP可靠稳定没有关系,TCP的可靠是通过重传和检错等机制实现的。 默认创建一个socket后ÿ…...
爬山算法全解析:掌握优化技巧,攀登技术高峰!
一、引言 爬山算法是一种局部搜索算法,它基于当前解的邻域中进行搜索,通过比较当前解与邻域解的优劣来更新当前解,从而逐步逼近最优解。本文将对爬山算法进行详细的介绍。 二、爬山算法简介 爬山算法是一种基于贪心策略的优化算法ÿ…...
使用 Ollama框架 下载和使用 Llama3 AI大模型的完整指南
🏡作者主页:点击! 🤖AI大模型部署与应用专栏:点击! ⏰️创作时间:2024年5月24日20点59分 🀄️文章质量:96分 目录 💥Ollama介绍 主要特点 主要优点 应…...
最新流媒体在线音乐系统网站源码| 音乐社区 | 多语言 | 开心版
最新流媒体在线音乐系统网站源码 源码免费下载地址抄笔记 (chaobiji.cn)...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
