leecode 226 翻转二叉树、101 对称二叉树、104 二叉树的最大深度
leecode 226 翻转二叉树、101 对称二叉树、104 二叉树的最大深度
leecode 226 翻转二叉树
题目链接 :https://leetcode.cn/problems/invert-binary-tree/description/
题目
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
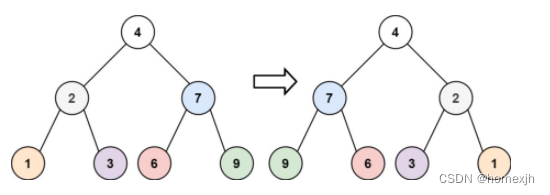
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:
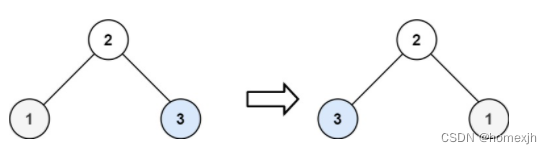
输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100
解题思路
这道题其实就是对二叉树的每个节点进行交换,其实就跟数值交换差不多,只不过这里是在二叉树。一般遇到二叉树相关题目,想一下使用哪一种遍历顺序,前中后。这道题来说,前序和后序基本都可以,如果是中序的话,某些节点可能要交换两次,因为中序遍历逻辑是左中右,在中进行交换,然后再遍历到右节点,这不是相当于把原来交换的再次交换了吗。具体实现代码为:
class Solution {public TreeNode invertTree(TreeNode root) {if (root == null) return root;traverseMid(root);return root;}public void traverse(TreeNode root) {if (root == null) return; //递归终止条件traverse(root.left); //左traverse(root.right); //右TreeNode tmp = root.left; //中root.left = root.right;root.right = tmp;}
}
//或者不用辅助函数
class Solution {public TreeNode invertTree(TreeNode root) {if (root == null) return root; //递归终止条件TreeNode left = invertTree(root.left); //左TreeNode right = invertTree(root.right); //右root.left = right; //中root.right = left;return root;}
}
leecode 101 对称二叉树
题目链接 :https://leetcode.cn/problems/symmetric-tree/description/
题目
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
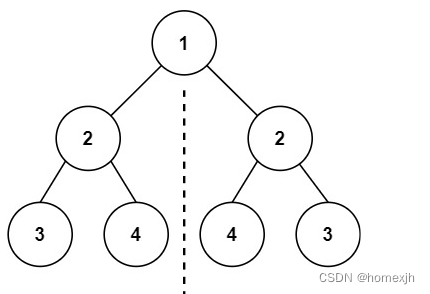
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
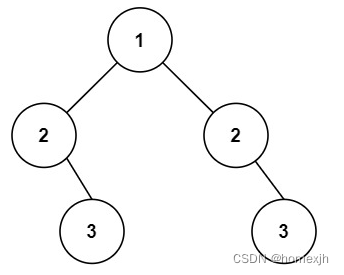
输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100
解题思路
这道题我们要清楚,要比较的不是左右节点,而是根节点的左右两棵树,所以在遍历的过程中,两棵树要同时遍历。那要哪种遍历顺序呢,因为同时比较两棵树的左右节点,那哪个遍历顺序通过返回值是能拿到左右节点信息的呢。就是后续遍历了。
那这道题的递归终止条件是什么呢,这道题是个判断题,一旦有符合的就直接返回。从示例中可以看到,左子树的左节点的值要等于右子树的右节点的值,左子树的右节点的值要等于右字数的左节点的值。所以这个是递归中的语句。那不满足的就是返回false就行了,递归条件有以下几种:
1.左子树为空右子树不为空 if (left == null && right != null) return false;
2.左子树不为空右子树为空 if (right == null && left != null) return false
3.左子树和右子树都为空,这是符合的 if (left == null && right == null) return true;
4.左子树的值不等于右子树的值 if (left.val != right.val) return false;
其中第4点一定是在前面三点判断完后开始判断,因为要不为空才有值。
class Solution {public boolean isSymmetric(TreeNode root) {return compare(root.left,root.right); //两棵树同时遍历}public boolean compare(TreeNode left,TreeNode right) {if (left == null && right != null) return false; //1.左子树为空右子树不为空if (right == null && left != null) return false; //2.左子树不为空右子树为空if (left == null && right == null) return true; //3.左子树和右子树都为空if (left.val != right.val) return false; //4.左子树的值不等于右子树的值boolean out = compare(left.left,right.right); //左boolean inner = compare(left.right,right.left); //右return out && inner; //中}
}
leecode 104 二叉树的最大深度
题目链接 :https://leetcode.cn/problems/maximum-depth-of-binary-tree/description/
题目
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
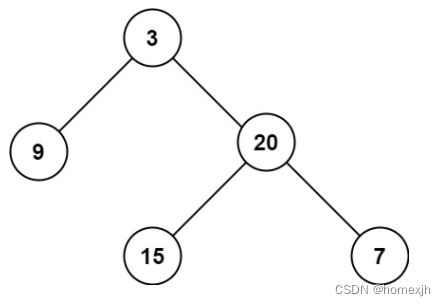
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示:
树中节点的数量在 [0, 104] 区间内。
-100 <= Node.val <= 100
解题思路
这道题用层序遍历可以套模板。这篇文章主要是说二叉树的递归。对于二叉树的最大深度,最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。那我们可以用前序遍历一路遍历下去,遍历到下一层,深度加一,不过要注意的是,在返回去的时候,深度要相应的减一,此时就涉及到回溯了。也可以用后序遍历,拿到左右值后深度加一。注意递归结束条件,是当root==null,return 0;取左右子树深度的最大值加上根节点这一层即可。当然,中序遍历也是一样的。具体代码为:
//后序遍历
class Solution {public int maxDepth(TreeNode root) { if (root == null) return 0; //递归终止条件int left = maxDepth(root.left); //左int right = maxDepth(root.right); //右return Math.max(left,right) + 1; //中}
}
//前序遍历
class Solution {int res = 0;public int maxDepth(TreeNode root) {int length = 0;traverse(root,length);return res;}public void traverse(TreeNode root,int length) {if (root == null) return;length++;res = Math.max(res,length); //中traverse(root.left,length); //左traverse(root.right,length); //右length--; //回溯}
}
//中序遍历
class Solution {int res = 0;public int maxDepth(TreeNode root) {int length = 0;traverse(root,length);return res;}public void traverse(TreeNode root,int length) {if (root == null) return;length++;traverse(root.left,length); //左res = Math.max(res,length); //中traverse(root.right,length); //右length--; //回溯}
}
相关文章:

leecode 226 翻转二叉树、101 对称二叉树、104 二叉树的最大深度
leecode 226 翻转二叉树、101 对称二叉树、104 二叉树的最大深度 leecode 226 翻转二叉树 题目链接 :https://leetcode.cn/problems/invert-binary-tree/description/ 题目 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。…...

Redux基础
简介 状态管理工具,集中式管理react、vue、angular等应用中多个组件的状态,是一个库,使用之后可以清晰的知道应用里发生了什么以及数据是如何修改,如何更新的 在项目中添加 Redux 并不是必须的,根据项目需求选择是否引入 Redux 三个原则 …...

国外目标公司的任何一个联系人也许都有意义
我们说跟进一个项目,最好能够联系上拥有决策权的人,不然中间隔着几重关系,所有的更新都需要层层审批申报,特别麻烦,总是要等,也许等到最后就是一场空。如果能够直接和老板或者是拍板的人沟通,则…...

因为本地证书太旧或不全导致的 HTTPS 访问失败问题20240520
因为本地证书太旧或不全导致的 HTTPS 访问失败问题 在生产环境中,我们经常需要使用 curl 命令来测试和调试 HTTPS URL。然而,最近我遇到了一个棘手的问题:在测试环境中使用 curl 可以正常访问某个 URL,但在生产环境中却遇到了 SS…...

Lua获取表的长度
1.代码 -- 创建一个表并添加一些元素 local myTable {10, 20, 30, 40}-- 打印表的长度 print(#myTable) -- 输出 4,因为表中有 4 个元素-- 使用 # 来遍历表中的所有元素 for i 1, #myTable doprint(myTable[i]) end -- 这将依次打印 10, 20, 30, 40...

python九九乘法表的打印思考及实现
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一、问题引入 九九乘法表的显示需求 二、问题分析 嵌套循环的概念 屏幕宽度与换行的考虑…...

2.Spring中用到的设计模式
Spring框架中使用了多种设计模式来构建其强大且灵活的功能,这里举例说明Spring中的一些功能使用到的设计模式。 工厂模式:Spring容器本质是一个大工厂,使用工厂模式通过BeanFactory和ApplicationContext这两个核心接口来创建和管理bean对象。…...
.NET调用阿里云人脸核身服务端 (ExecuteServerSideVerification)简易流程保姆级教学
需要注意的是,以下内容仅限基础调用 功能说明 该功能是输入核验人的姓名和身份证以及人脸照片,去阿里库里面匹配,3个信息是否一致,一致则验证通过,需要注意的是,人脸有遮挡,或者刘海࿰…...
]C语言堆排序技术详解)
[大师C语言(第十二篇)]C语言堆排序技术详解
引言 堆排序(Heap Sort)是一种基于比较的排序算法,它利用堆这种数据结构的特点来进行排序。堆是一种近似完全二叉树的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父…...

Activity启动流程要点
一、Activity启动流程 Activity的启动流程一般是通过调用startActivity或者是startActivityForResult来开始的startActivity内部也是通过调用startActivityForResult来启动Activity,只不过传递的requestCode小于0Activity的启动流程涉及到多个进程之间的通讯这里主…...

lua 计算第几周
需求 计算当前赛季的开始和结束日期,2024年1月1日周一是第1周的开始,每两周是一个赛季。 lua代码 没有处理时区问题 local const 24 * 60 * 60 --一整天的时间戳 local server_time 1716595200--todo:修改服务器时间 local date os.date("*t…...
负载均衡策略
...

海外网红营销新趋势:“快闪式”营销如何迅速提升品牌曝光度
在当今数字化时代,海外网红营销已成为品牌迅速触达全球消费者、提升品牌曝光度和刺激销售的重要手段。其中,“快闪式”营销以其独特的时效性、创意性和互动性,成为品牌与海外网红合作的新趋势。本文Nox聚星将和大家探讨如何利用海外网红的影响…...

速看!打造专属数字化能力模型的七大关键!
在数字化浪潮中,企业如何打造适应自身发展的数字化能力模型?这是许多企业面临的重要课题。今天,通过众多企业使用蚓链数字化生态解决方案实践总结,为大家分享至关重要的七大经验,助你开启数字化转型之旅! 1…...

青蛙跳台阶问题
本期介绍🍖 主要介绍:青蛙跳台阶问题,青蛙跳台阶与斐波那契数列的关系👀。 文章目录 1. 题目2. 递归解题思路3. 迭代解题思路 1. 题目 从前有一只青蛙他想跳台阶,有n级台阶,青蛙一次可以跳1级台阶ÿ…...

linux日常运维2
下载linux离线安装包---- 利用 Downloadonly 插件下载 RPM 软件包及其所有依赖包 1. 先找个可以上网的linux操作系统,这里是以centos7操作系统为例,如果要使用centos6就先安装一个centos6的系统,然后让他可以上网,后面步骤如下 a.…...
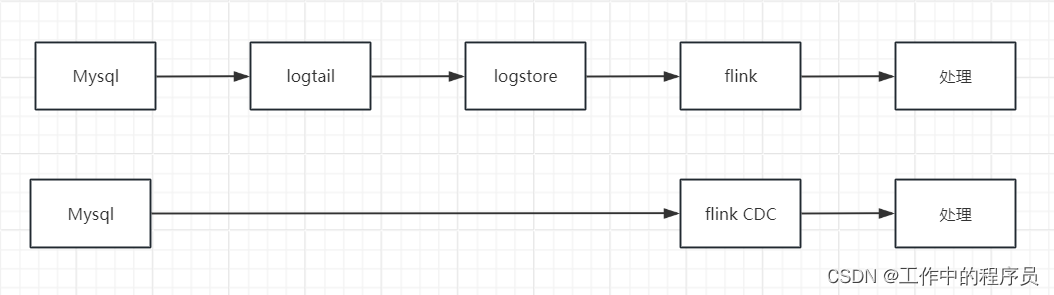
flink cdc mysql整理与总结
文章目录 一、业务中常见的需要数据同步的场景CDC是什么FlinkCDC是什么CDC原理为什么是FlinkCDC业务场景flink cdc对应flink的版本 二、模拟案例1.阿里云flink sql2.开源flink sql(单机模式)flink 安装安装mysql3.flink datastream 三、总结 提示:以下是本篇文章正文…...
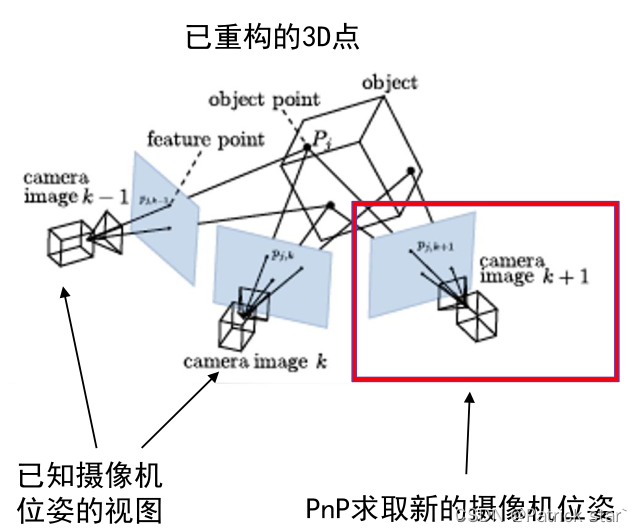
【三维重建】ePnP
PnP问题应用与一下场景: 已知三维点和对应二维点以及相机相机内参数,可以获取相机外参。 我们介绍其中的一种算法:ePnP 算法流程 1、ePnP算法首先在世界坐标系内寻找4个控制点,记作 C 1 w , C 2 w , C 3 w , C 4 w C_1^w,C_2^w,…...

C++进阶之路:何为运算符重载、赋值运算符重载与前后置++重载(类与对象_中篇)
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...
8、python基础知识图谱
...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...
