VMware ESXi中安装Proxmox VE
0、巴拉巴拉
前几天某行业HW,闲暇的时候几个技术人员聊天,臭味相投的聊到自己玩的东西。有个玩家说家里用工作站安装Proxmox VE,然后在上面安装软路由、安装NAS。我以前一直想玩玩,没有付诸行动,所以也想弄个集中的方案,比如可以把Tails、Batocera、等好玩的整到一起。今天记录一下,改天收集资源整合一下。
我没有工作站,但是手头上有一套VMware ESXi,可以利用这个环境安装。
首先下载镜像文件:
Downloads - Proxmox Virtual Environment
顺便装个软路由,下载地址:
Index of /releases/23.05.3/targets/x86/64/

1、开始安装
在VMware ESXi内新建虚拟机,配置合适的资源和网络,需要注意的是CPU需要打开虚拟化。

设置光驱为ISO文件,可以上传到ESXi的存储空间。

然后启动,看到开始界面。

过程略。
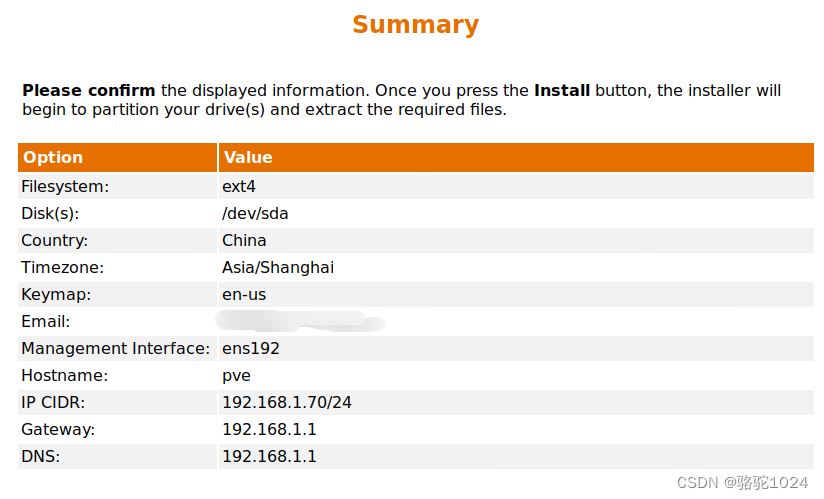
安装完成后就可以使用浏览器管理。


2、安装OpenWrt
将下载好的文件进行解压,得到img文件。
然后把img文件上传,记住窗口中的路径。

/var/lib/vz/template/iso/openwrt-23.05.2-x86-64-generic-ext4-combined-efi.img
或者在PVE系统的shell使用find命令里查找。
新建虚拟机,不使用任何介质,删除硬盘。

这时候打开shell,执行:
qm disk import 100 /var/lib/vz/template/iso/openwrt-23.05.2-x86-64-generic-ext4-combined-efi.img local-lvm
网上其他文档说是importdisk命令,可能版本变动,命令进行了修改。

提示导入成功。
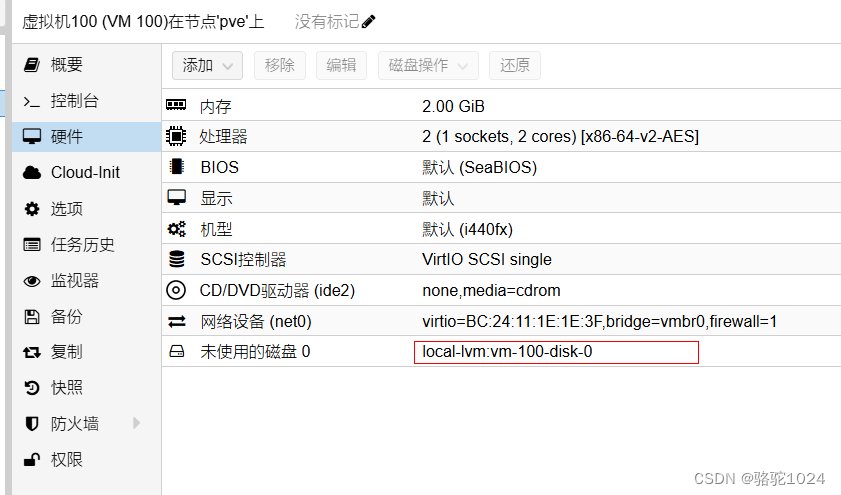
双击未使用磁盘,进行添加。

这一步很重要,刚开始我没看到,从别的帖子里看到并进行截图。
然后就开始了安装过程。

这个界面回车进入shell。
vi /etc/config/network,修改IP地址。

service network restart,重启网络。
passwd,修改密码。
所有设置完毕竟然发现pve和openwrt之间可以互通,pve和其他主机可以互通,但是openwrt和外部无法通讯。分析半天我估计是ESXi平台的问题。
果然,交换机端口组需要开启混杂模式。

设置完毕以后马上可以打开。

设置路由,刚才网络设置里没有,这一步需要设置路由。

记得点击save&apply。
设置dns,在接口--编辑--高级--自定义DNS服务器。
网络通了以后首先进行更新。
opkg update更新完毕后设置中文。
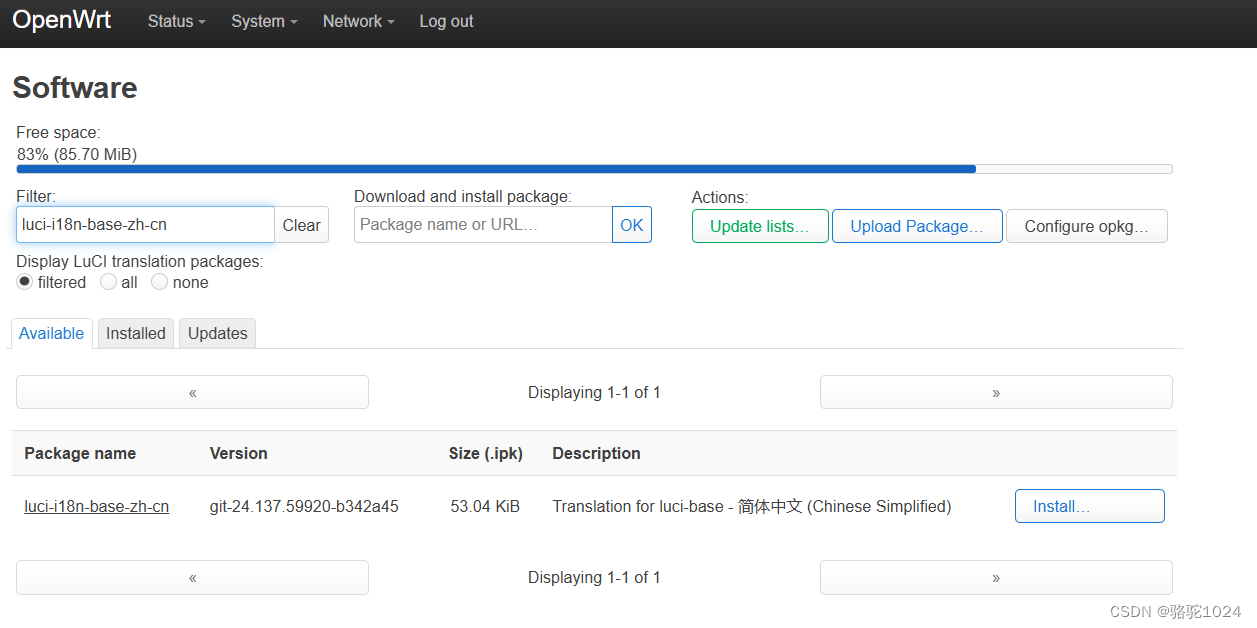
至于更详细的设置目前没有测试。
仅作为安装的话到这里就告一段落。
3、总结
想做和真的做起来过程也是有点曲折的,不过也是享受的过程。其他的系统也可以试着try一下。
相关文章:

VMware ESXi中安装Proxmox VE
0、巴拉巴拉 前几天某行业HW,闲暇的时候几个技术人员聊天,臭味相投的聊到自己玩的东西。有个玩家说家里用工作站安装Proxmox VE,然后在上面安装软路由、安装NAS。我以前一直想玩玩,没有付诸行动,所以也想弄个集中的方案…...

Java(其十二)--集合·初级
ArrayList集合 集合有很多种,ArrayList 是最常用的一种,集合的作用相当于C中的STL 最显著的特点就是:自动扩容。 一般定义式 ArrayList list new ArrayList(); //该 list 是可以储存各种类型的数据的,要想约束储存的数据&#x…...

疯狂“造人”!美国两党共推新法案,5年培养100万AI及量子人才
当前,全球量子计算人才的短缺已成为制约该领域快速发展的关键瓶颈。 为了解决量子计算人才短缺的问题,各国政府和企业采取了积极措施,加大了对量子教育和培训的投入。根据美国参议院官网消息,2024年5月23日,美国两党议…...

Python 文件操作指南:使用 open 和 with open 实现高效读写
🍀 前言 博客地址: CSDN:https://blog.csdn.net/powerbiubiu 👋 简介 本系列文章主要分享文件操作,了解如何使用 Python 进行文件的读写操作,介绍常见文件格式的读取和写入方法,包括TXT、 CS…...

FasterNet代码阅读
FasterNet 类参数初始化 将图像切分为非重叠的图像块 PatchEmbed 类 将图像分解为非重叠的图像块有以下几个好处: 1. 缩小计算量:对于大尺寸的图像,直接对整个图像进行处理可能会导致计算和内存消耗过大。将图像切分为小块可以降低计算量…...
Rust开源Web框架Salvo源码编译
1.克隆源码: https://github.com/salvo-rs/salvo.git 2.进入salve目录并运行cargo build编译 编译成功 3.编译生成的库 4.安装salve-cli git clone --recursive https://github.com/salvo-rs/salvo-cli.git 编译salve-cli...
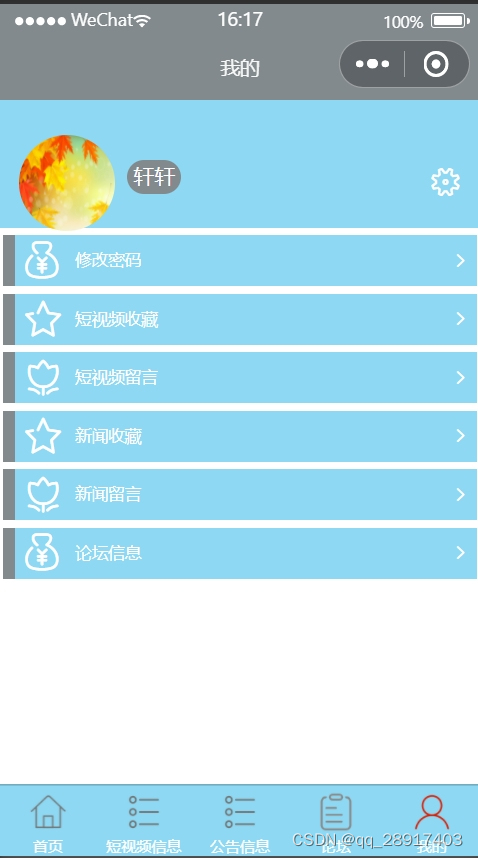
基于Java+SpringBoot+Mybaties-plus+Vue+elememt + uniapp 新闻资讯 的设计与实现
一.项目介绍 本系统分为 后端 和 小程序端 后端:点击登录按钮 设置个人中心、 管理员账号数据维护、 基础数据维护、 短视频信息维护(包括查看短视频留言、短视频收藏)、 论坛维护(增删改查帖子信息,包括查…...
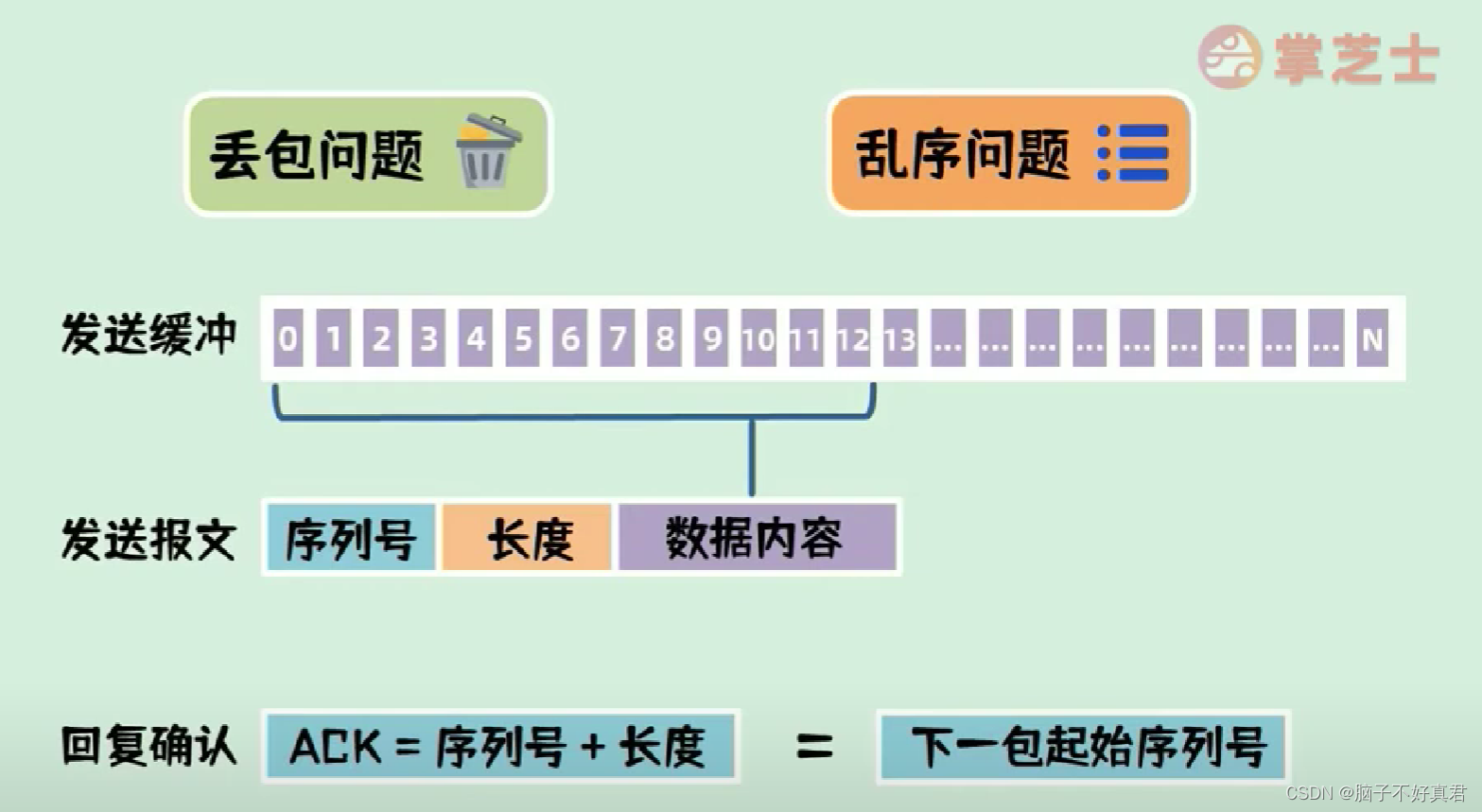
TCP—三次握手和四次挥手
目录 一、三次握手和四次挥手的目的 二、TCP可靠的方面 三、什么是三次握手 四、第三次握手的目的 五、什么是四次挥手 六、超时时间的目的 七、SYN包、ACK包、FIN包 八、解决丢包和乱序 九、参考资料 一、三次握手和四次挥手的目的 TCP三次握手的目的主要是为了确保两…...

基于UDP的网络聊天室
一.项目需求: 如果有用户登录,其他用户可以收到这个人的登录信息如果有人发送信息,其他用户可以收到这个人的群聊信息如果有人下线,其他用户可以收到这个人的下线信息服务器可以发送系统信息 二.服务器端 #include <myhead.h&…...
数组-两个升序数组中位数
一、题目描述 二、解题思路 (一).基本思想: 如果列表总长度allsize( arr1.size()arr2.size() ) 为奇数时,中位数位置应该在两个列表排序后的第 allsize/2 位置处,如果allsize为偶数,中位数应该取 (allsize/2)-1 和 allsize/2 的…...

每日一题《leetcode--116.填充每个结点的下一个右侧结点》
https://leetcode.cn/problems/populating-next-right-pointers-in-each-node/ 题目要求给每个结点的next指针进行填充,使每个结点的next指针指向其下一个右侧结点。如果右侧没有结点,则将next指针设置为空。 struct Node* connect(struct Node* root) {…...
-磁盘结构(5)-Redolog)
【MySQL精通之路】InnoDB(6)-磁盘结构(5)-Redolog
主博客: 【MySQL精通之路】InnoDB(6)-磁盘上的InnoDB结构-CSDN博客 上一篇: 【MySQL精通之路】InnoDB-双写缓冲区-CSDN博客 下一篇: 目录 1.配置Redo Log容量(MySQL 8.0.30或更高版本) 2.配置重做日志容量(MySQL…...

【探索自然语言处理:构建一个简单的文本分类器】
文章目录 前言文本预处理特征提取模型训练文本分类结论 前言 在信息时代,文本数据无处不在,从社交媒体帖子到客户反馈,文本是沟通和信息交流的主要媒介。自然语言处理(NLP)是人工智能的一个分支,它使计算机…...

概率论统计——大数定律
大数定律 弱大数定律(辛钦大数定律) 利用切比雪夫不等式,证明弱大数定律 应用 伯努利大数定理,(辛钦大数定理的推论) 证明伯努利大数定理 注意:这里将二项分布转化成0,1分布来表示,…...

vscode终端命令行前面出现两个conda环境名的问题决解方法
已经安装了conda,打开vscode的terminal时,命令行前面有两个虚拟环境名。 进入vscode的setting 找到Python->Python:Default Interpreter Path,把这个值复位,就可以解决。 如果不想前面带(base),可以运行 conda co…...

“AI黏土人”一夜爆火,图像生成类应用应该如何长期留住用户?
文章目录 最近大火的“AI黏土人”,一股浓浓的《小羊肖恩》风。 凭借这这种搞怪的风格,“AI黏土人”等图像生成类应用凭借其创新技术和市场需求迅速崛起并获得巨大关注。然而,要保持用户黏性并确保长期发展,这些应用需要采取一系列…...
-查询优化(12)-块嵌套循环和批处理Key访问联接)
【MySQL精通之路】SQL优化(1)-查询优化(12)-块嵌套循环和批处理Key访问联接
在MySQL中,可以使用批处理Key访问(BKA)联接算法,该算法使用对联接表的索引访问和联接缓冲区。 BKA算法支持内联接、外联接和半联接操作,包括嵌套的外部联接。 BKA的优点包括由于更高效的表扫描而提高了联接性能。 此…...
SQL使用函数给多个分表添加同一字段
数据库中分表时,往往需要向多个分表中添加同一个字段,可以定义一个函数,每次调用这个函数向多个份表中添加同意字段。 1、创建函数示例: 在PostgreSQL中创建一个简单的函数 以下是一个在PostgreSQL中创建函数的简单示例&#x…...

OpenAI 再次刷新认知边界:GPT-4 颠覆语音助手市场,流畅度直逼真人互动?
前言 近日,美国人工智能研究公司 OpenAI 发布了其最新旗舰模型 GPT-4o,这一革命性的进展不仅标志着人工智能领域的新突破,更预示着即将步入一个全新的交互时代?GPT-4o 的发布,对于我们来说,意味着人工智能…...
UE5 使用外置摄像头进行拍照并保存到本地
连接外置摄像头功能:https://docs.unrealengine.com/4.27/zh-CN/WorkingWithMedia/IntegratingMedia/MediaFramework/HowTo/UsingWebCams/ 核心功能:UE4 相机拍照功能(图片保存)_ue 移动端保存图片-CSDN博客 思路是: …...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
