统计计算四|蒙特卡罗方法(Monte Carlo Method)
系列文章目录
统计计算一|非线性方程的求解
统计计算二|EM算法(Expectation-Maximization Algorithm,期望最大化算法)
统计计算三|Cases for EM
文章目录
- 系列文章目录
- 一、基本概念
- (一)估算 π \pi π
- (二)求积分
- (三)使用步骤
- 二、变换采样
- (一)基本概念
- (二)相关定理
- (三)示例
- 三、逆变换采样
- (一)相关定理
- (二)逆变换法
- (三)采样步骤
- (四)示例
- 四、接受拒绝采样
- (一)基本概念
- (二)工作原理
- (三)采样步骤
- (四)示例
- 五、重要性采样
- (一)基本概念
- (二)蒙特卡洛估计
- (三)示例
一、基本概念
蒙特卡洛方法:为了解决某确定性问题,把它变成一个概率模型的求解问题,然后产生符合模型的大量随机数,对产生的随机数进行分析从而求解问题的方法,又称为随机模拟方法。
- 随机数:设 X X X 是具有分布函数 F ( x ) F(x) F(x) 的随机变量,从分布 F ( x ) F(x) F(x) 中随机抽样得到的序列 { x i , i = 1 , 2 , . . . } \{x_i, i = 1, 2, ...\} {xi,i=1,2,...} 称为该分布的随机数序列, x i x_i xi 称为分布 F ( x ) F(x) F(x) 的随机数。
(一)估算 π \pi π
向正方形 D = { ( x , y ) : x ∈ [ 0 , 1 ] , y ∈ [ 0 , 1 ] } D=\{(x,y):x\in[0,1],y\in[0,1]\} D={(x,y):x∈[0,1],y∈[0,1]}内随机等可能投点,落入四分之一圆 C = { ( x , y ) : x 2 + y 2 ≤ 1 , x > 0 , y > 0 } C=\{(x,y):x^2+y^2\leq 1,x>0,y>0\} C={(x,y):x2+y2≤1,x>0,y>0}的概率为面积之比 p = π 4 p=\frac{\pi}{4} p=4π。如果独立重复地投了 n n n个点,落入 C C C中的点的个数为 ξ \xi ξ,则有:
ξ n ≈ π 4 , π ≈ π ^ = 4 ξ n \frac{\xi}{n}\approx \frac{\pi}{4},\ \pi\approx \hat{\pi}=\frac{4\xi}{n} nξ≈4π, π≈π^=n4ξ

由于 ξ \xi ξ服从 B i n o m i a l ( n , π 4 ) Binomial(n,\frac{\pi}{4}) Binomial(n,4π)分布,有:
V a r ( π ^ ) = π ( 4 − π ) 16 n Var(\hat{\pi})=\frac{\pi(4-\pi)}{16n} Var(π^)=16nπ(4−π)
由中心极限定理, π ^ \hat{\pi} π^近似服从 N ( π , π ( 4 − π ) 16 n ) N(\pi,\frac{\pi(4-\pi)}{16n}) N(π,16nπ(4−π))分布,所以随机模拟误差的幅度大约在 ± 2 π ( 4 − π ) 16 n \pm 2\sqrt{\frac{\pi(4-\pi)}{16n}} ±216nπ(4−π)(随机模拟误差95%以上落入此区间)
(二)求积分
将积分转化为期望来计算:对于 Q = ∫ a b h ( x ) d x Q=\int_a^bh(x)dx Q=∫abh(x)dx,取 U ∼ U ( a , b ) U\sim U(a,b) U∼U(a,b),有:
Q = ( b − a ) ∫ a b h ( u ) 1 b − a d u = ( b − a ) E [ h ( U ) ] Q=(b-a)\int_a^bh(u)\frac{1}{b-a}du=(b-a)E[h(U)] Q=(b−a)∫abh(u)b−a1du=(b−a)E[h(U)]
若取 { U i , i = 1 , . . . , N } \{U_i,i=1,...,N\} {Ui,i=1,...,N}独立同 U ( a , b ) U(a,b) U(a,b)分布,并设 Y i = h ( U i ) , i = 1 , 2 , . . . , N Y_i=h(U_i),i=1,2,...,N Yi=h(Ui),i=1,2,...,N是 i i d iid iid随机变量列,由强大数律:
Y ˉ = 1 N ∑ i = 1 N h ( U i ) → E h ( U ) = Q b − a , a . s . ( N → ∞ ) \bar{Y}=\frac{1}{N}\sum_{i=1}^Nh(U_i)\rightarrow Eh(U)=\frac{Q}{b-a},\ a.s.(N\rightarrow ∞) Yˉ=N1i=1∑Nh(Ui)→Eh(U)=b−aQ, a.s.(N→∞)
于是有:
Q ^ = ( b − a ) Y ˉ = b − a N ∑ i = 1 N h ( U i ) \hat{Q}=(b-a)\bar{Y}=\frac{b-a}{N}\sum_{i=1}^Nh(U_i) Q^=(b−a)Yˉ=Nb−ai=1∑Nh(Ui)
由中心极限定理:
N ( Q ^ − Q ) → d N ( 0 , ( b − a ) 2 V a r ( h ( U ) ) ) \sqrt{N}(\hat{Q}-Q)\xrightarrow{d} N(0,(b-a)^2Var(h(U))) N(Q^−Q)dN(0,(b−a)2Var(h(U)))
V a r [ h ( U ) ] = ∫ a b [ h ( u ) − E h ( U ) ] 2 1 b − a d u Var[h(U)]=\int_a^b[h(u)-Eh(U)]^2\frac{1}{b-a}du Var[h(U)]=∫ab[h(u)−Eh(U)]2b−a1du
V a r [ ( h ( U ) ] Var[(h(U)] Var[(h(U)]可以用模拟样本 { Y i = h ( U i ) } \{Y_i=h(U_i)\} {Yi=h(Ui)}估计为:
V a r ( h ( U ) ) ≈ 1 N ∑ i = 1 N ( Y i − Y ˉ ) 2 Var(h(U))\approx\frac{1}{N}\sum_{i=1}^N(Y_i-\bar{Y})^2 Var(h(U))≈N1i=1∑N(Yi−Yˉ)2
(三)使用步骤
蒙特卡洛方法的理论基础是大数定律。样本数量越多,则随机数的平均值就越接近期望,也就是要计算的真实值。
- 将实际问题转化为求期望,并定义要采样的随机变量
- 计算机模拟采样过程,处理产生的随机数得到期望
二、变换采样
(一)基本概念
如果随机变量 η η η 不容易抽样,但是存在另一个容易抽样的随机变量 ξ ξ ξ 和随机变量 η η η 间具有一一对应关系,即 η = h ( ξ ) η = h(ξ) η=h(ξ) 或 ξ = h − 1 ( η ) ξ = h^{−1}(η) ξ=h−1(η),同分布。那么可以先产生随机变量 ξ ξ ξ,再由函数关系 h ( ⋅ ) h(·) h(⋅) 得到随机变量 η η η,这种产生随机数的方法称为变换抽样法。
(二)相关定理
设随机变量 ξ \xi ξ具有概率密度函数 f ( x ) f(x) f(x),另有一函数 h ( ⋅ ) h(·) h(⋅)严格单调,其反函数记为 h − 1 ( ⋅ ) h^{-1}(·) h−1(⋅)且导函数存在,则 η = h ( ξ ) \eta=h(\xi) η=h(ξ)是随机变量 ξ \xi ξ的函数,其概率密度函数为:
p ( z ) = f ( h − 1 ( z ) ) ⋅ ∣ { h − 1 ( z ) } ′ ∣ p(z)=f(h^{-1}(z))·|\{h^{-1}(z)\}'| p(z)=f(h−1(z))⋅∣{h−1(z)}′∣
证明:
(三)示例
-
用变换抽样法产生分布为 N ( µ , σ 2 ) N(µ, σ2) N(µ,σ2) 的随机数。

-
用变换抽样法产生分布为 G a m m a ( 1 / 2 , 3 ) Gamma(1/2, 3) Gamma(1/2,3) 的随机数。

三、逆变换采样
(一)相关定理
假设 X X X为一个连续随机变量,其累计分布函数为 F X F_X FX,此时可证明随机变量 Y = F X ( X ) Y=F_X(X) Y=FX(X)服从区间 [ 0 , 1 ] [0,1] [0,1]上的均匀分。逆变换采样就是将上述过程反过来进行。
设连续型随机变量 η \eta η的分布函数 F ( x ) F(x) F(x)是连续且严格单调上升的分布函数,其反函数存在且记为 F − 1 ( x ) F^{-1}(x) F−1(x)。则有:
- 随机变量 F ( η ) F(\eta) F(η)服从 ( 0 , 1 ) (0,1) (0,1)上的均匀分布,即 F ( η ) ∼ U ( 0 , 1 ) F(\eta)\sim U(0,1) F(η)∼U(0,1)
- 对于随机变量 U ∼ U ( 0 , 1 ) U\sim U(0,1) U∼U(0,1), F − 1 ( U ) F^{-1}(U) F−1(U)的分布函数为 F ( x ) F(x) F(x)
证明:
(二)逆变换法
逆变换法:当随机变量 η \eta η的分布函数 F ( x ) F(x) F(x)的反函数存在,且容易计算时,可通过产生均匀分布的随机数来产生 η \eta η的随机数序列 { η i , i = 1 , 2 , . . . } \{\eta_i,i=1,2,...\} {ηi,i=1,2,...}。这种产生非均匀分布随机数的方法称为逆变换法或反函数法。
(三)采样步骤
- 产生 U ( 0 , 1 ) U(0,1) U(0,1)的随机数序列 { u i , i = 1 , 2 , . . . } \{u_i,i=1,2,...\} {ui,i=1,2,...}
- η \eta η的随机数序列为:
η i = F − 1 ( u i ) , i = 1 , 2 , . . . \eta_i=F^{-1}(u_i),i=1,2,... ηi=F−1(ui),i=1,2,...
(四)示例
- 产生概率密度函数为 f(x) 的随机数,其中:
f ( x ) = { x σ 2 e − x 2 2 σ 2 , x > 0 0 , z ≤ 0 f(x) = \begin{cases} \frac{x}{\sigma^2}e^{-\frac{x^2}{2\sigma^2}}, & \text{$x>0$} \\ 0, & \text{$z\leq0$} \end{cases} f(x)={σ2xe−2σ2x2,0,x>0z≤0

- 产生分布函数为 F ( x ) F(x) F(x) 的随机数 η η η,其中
F ( x ) = x 2 + x 2 , 0 ≤ x ≤ 1 F(x)=\frac{x^2+x}{2},0\leq x\leq 1 F(x)=2x2+x,0≤x≤1

四、接受拒绝采样
(一)基本概念
拒绝抽样是基于以下观察而提出的:要在一维中抽样一个随机变量,可以对二维笛卡尔图进行均匀随机抽样,并将样本保留在其密度函数图形下的区域中。
想象将一个随机变量的密度函数绘制在一个大矩形板上,并向其投掷飞镖。假设这些飞镖在整个板上均匀分布。现在移除所有落在曲线下方以外区域的飞镖。剩下的飞镖将在曲线下方的区域内均匀分布,并且这些飞镖的 x 坐标将按照随机变量的密度分布。这是因为在曲线最高的地方,也就是概率密度最大的地方,飞镖着陆的空间最多。
拒绝抽样的一般形式假设板子的形状不一定是矩形,而是根据某个提议分布的密度来确定(该分布不一定归一化为 1)。通常情况下将其视为某个已知的分布的倍数。提议分布中的每个点至少与想要抽样的分布一样高,以便前者完全包围后者。(否则,想要抽样的曲线区域中的某些部分可能永远无法到达。)

(二)工作原理
拒绝抽样的工作原理:
- 从提议分布中在 x 轴上抽样一个点。
- 在该 x 位置上画一条竖直线,直到提议分布的概率密度函数的 y值。
- 在这条线上从 0 到提议分布的概率密度函数的 y 值之间均匀抽样。如果抽样值大于该竖直线上所需分布的密度函数值,则拒绝该 x 值并返回第 1 步;否则,该 x 值就是所需分布的一个样本。
拒绝抽样算法可以用于从任何曲线下方进行抽样,无论函数是否积分为 1。事实上,通过常数缩放函数对抽样的 x 位置没有影响。因此,该算法可以用于从归一化常数未知的分布中进行抽样。
(三)采样步骤
提案分布 g g g:为了从密度为 f f f的分布 X X X中获取样本,利用了容易采样的密度函数为 g g g的分布 Y Y Y, g g g就是提案分布
设 M M M为似然比 f ( x ) / g ( x ) f(x)/g(x) f(x)/g(x)的上界,即一个常数满足 1 ≤ M < ∞ 1\leq M<∞ 1≤M<∞。也就是说 M M M必须满足 f ( x ) ≤ M g ( x ) f(x)\leq Mg(x) f(x)≤Mg(x)对任意 x x x都成立,因此 Y Y Y分布的支撑要包含 X X X的支撑
- 从分布 Y Y Y获取样本 y ∼ g y\sim g y∼g,并从 U n i f ( 0 , 1 ) Unif(0,1) Unif(0,1)(单位区间上的均匀分布)获取样本 u u u
- 检查是否 u < f ( y ) / M g ( y ) u<f(y)/Mg(y) u<f(y)/Mg(y).( M ≥ 1 M\geq 1 M≥1)
- 成立则接受 y y y作为从 f f f中抽取的样本
- 不成立则拒绝 y y y的值并重新获取样本
保留样本不大于值 y 的概率为:

其中 P [ U ≤ f ( Y ) M g ( Y ) ] = 1 M P[U\leq \frac{f(Y)}{Mg(Y)}]=\frac{1}{M} P[U≤Mg(Y)f(Y)]=M1为接受率,接受率越大,采样效率就越高。接受拒绝算法平均需要 M 次迭代才能获得样本,并且M 越小越好,即包络线越贴近目标分布越好,可设
M = max x f ( x ) g ( x ) M=\max_x \frac{f(x)}{g(x)} M=xmaxg(x)f(x)

(四)示例
试用接受拒绝采样产生服从均值为 0,方差为 1 的半正态分布的随机数 η η η,该分布的概率密度函数为
p ( z ) = { 2 / π e − z 2 2 , z ≥ 0 0 , z < 0 p(z) = \begin{cases} \sqrt{2/\pi}e^{-\frac{z^2}{2}}, & \text{$z\geq0$} \\ 0, & \text{$z<0$} \end{cases} p(z)={2/πe−2z2,0,z≥0z<0

五、重要性采样
(一)基本概念
接受拒绝采样完美的解决了累积分布函数不可求时的采样问题。但是接受拒绝采样非常依赖于提议分布的选择,如果提议分布选择的不好,可能采样时间很长却获得很少满足分布的粒子。而重要性采样就解决了这一问题。
重要性采样是使用蒙特卡洛方法估算积分 (期望) 时,提高对积分计算重要区域的抽样,从而达到减少方差的目的。
μ = E X ∼ f ( h ( X ) ) = ∫ h ( x ) f ( x ) d x = ∫ h ( x ) f ( x ) g ( x ) g ( x ) d x \mu=E_{X\sim f}(h(X))=\int h(x)f(x)dx=\int h(x)\frac{f(x)}{g(x)}g(x)dx μ=EX∼f(h(X))=∫h(x)f(x)dx=∫h(x)g(x)f(x)g(x)dx
或若 ∫ f ( x ) ≠ 1 \int f(x)\neq 1 ∫f(x)=1, 也就是只知道分布成比例于某个函数,差一个归一化常数,则
μ = E X ∝ f ( h ( X ) ) = ∫ h ( x ) f ( x ) ∫ f ( x ) d x d x = ∫ h ( x ) f ( x ) g ( x ) g ( x ) d x ∫ f ( x ) g ( x ) g ( x ) d x \mu=E_{X∝f}(h(X))=\int h(x)\frac{f(x)}{\int f(x)dx}dx=\frac{\int h(x)\frac{f(x)}{g(x)}g(x)dx}{\int \frac{f(x)}{g(x)}g(x)dx} μ=EX∝f(h(X))=∫h(x)∫f(x)dxf(x)dx=∫g(x)f(x)g(x)dx∫h(x)g(x)f(x)g(x)dx
(二)蒙特卡洛估计
上式建议用来估计 E h ( X ) Eh(X) Eh(X) 的一种 Monte Carlo 方法:
-
从 g g g中抽取独立同分布的样本 X 1 , . . . , X n X_1,...,X_n X1,...,Xn,并采用估计:
μ ^ I S ∗ = 1 n ∑ i h ( x i ) f ( x i ) g ( x i ) → E X ∼ g ( h ( x ) f ( x ) g ( x ) ) \hat{\mu}^*_{IS}=\frac{1}{n}\sum_ih(x_i)\frac{f(x_i)}{g(x_i)}\rightarrow E_{X\sim g}(h(x)\frac{f(x)}{g(x)}) μ^IS∗=n1i∑h(xi)g(xi)f(xi)→EX∼g(h(x)g(x)f(x)) -
可以写成:( w ∗ ( X i ) = f ( X i ) / g ( X i ) w^*(X_i)=f(X_i)/g(X_i) w∗(Xi)=f(Xi)/g(Xi)是未标准化权重,称为重要性比率)
μ ^ I S ∗ = 1 n ∑ i h ( X i ) w ∗ ( X i ) \hat{\mu}^*_{IS}=\frac{1}{n}\sum_ih(X_i)w^*(X_i) μ^IS∗=n1i∑h(Xi)w∗(Xi) -
若是差一个比例常数的 f,则( w ∗ ( X i ) = w ∗ ( X i ) / ∑ i = 1 n w ∗ ( X i ) w^*(X_i)=w^*(X_i)/\sum_{i=1}^nw^*(X_i) w∗(Xi)=w∗(Xi)/∑i=1nw∗(Xi)是标准化权重)
μ ^ I S = 1 n ∑ i h ( X i ) w ( X i ) \hat{\mu}_{IS}=\frac{1}{n}\sum_ih(X_i)w(X_i) μ^IS=n1i∑h(Xi)w(Xi) -
估计值的方差是
V a r ( μ ^ ) = 1 n V a r h ( X ) f ( X ) g ( X ) = 1 n ∫ ( h ( x ) f ( x ) g ( x ) − μ 2 ) 2 g ( x ) d x = 1 n { ∫ ( h 2 ( x ) f 2 ( x ) g ( x ) d x − μ 2 } \begin{aligned} Var(\hat{\mu})=&\frac{1}{n}Var\frac{h(X)f(X)}{g(X)} \\ =&\frac{1}{n}\int (\frac{h(x)f(x)}{g(x)}-\mu^2)^2g(x)dx\\ =&\frac{1}{n}\{ \int(\frac{h^2(x)f^2(x)}{g(x)}dx-\mu^2\}\\ \end{aligned} Var(μ^)===n1Varg(X)h(X)f(X)n1∫(g(x)h(x)f(x)−μ2)2g(x)dxn1{∫(g(x)h2(x)f2(x)dx−μ2}
如果 h 2 ( x ) f 2 ( x ) / g 2 ( x ) = μ 2 {h^2(x)f^2(x)}/{g^2(x)}=\mu^2 h2(x)f2(x)/g2(x)=μ2,就有 V a r ( μ ^ ) = 0 Var(\hat{\mu})=0 Var(μ^)=0,即方差达到最小。此时:
g ( x ) = ∣ h ( x ) ∣ f ( x ) μ = ∣ h ( x ) ∣ f ( x ) ∫ ∣ h ( x ) ∣ f ( x ) d x g(x)=\frac{|h(x)|f(x)}{\mu}=\frac{|h(x)|f(x)}{\int |h(x)|f(x)dx} g(x)=μ∣h(x)∣f(x)=∫∣h(x)∣f(x)dx∣h(x)∣f(x)
密度函数 g ( x ) g(x) g(x) 的最佳选择就是和被积函数 ∣ h ( x ) ∣ f ( x ) |h(x)|f(x) ∣h(x)∣f(x) 具有相同的形状。对积分值贡献越大的区域,希望以较大的概率抽取到随机数。
在实际中, µ µ µ 是未知量,因此无法选取 g ( x ) g(x) g(x),使得 V a r ( µ ^ ) = 0 Var(\hat{µ}) = 0 Var(µ^)=0。通常情况下,我们会选取一个形状接近 ∣ h ( x ) ∣ f ( x ) |h(x)|f(x) ∣h(x)∣f(x) 的函数作为 g ( x ) g(x) g(x)。
μ = ∫ h ( x ) f ( x ) d x = ∫ h ( x ) f ( x ) g ( x ) g ( x ) d x \mu=\int h(x)f(x)dx=\int h(x)\frac{f(x)}{g(x)}g(x)dx μ=∫h(x)f(x)dx=∫h(x)g(x)f(x)g(x)dx

(三)示例
例:用重要抽样法估计 μ = ∫ 0 1 x f ( x ) d x = ∫ 0 1 e x d x \mu=\int_0^1xf(x)dx=\int_0^1e^xdx μ=∫01xf(x)dx=∫01exdx的估计值

参考:
MCMC入门(一)蒙特卡罗方法与拒绝-接受采样
相关文章:

统计计算四|蒙特卡罗方法(Monte Carlo Method)
系列文章目录 统计计算一|非线性方程的求解 统计计算二|EM算法(Expectation-Maximization Algorithm,期望最大化算法) 统计计算三|Cases for EM 文章目录 系列文章目录一、基本概念(一)估算 π \pi π(二&…...

大模型时代的具身智能系列专题(三)
清华高阳团队 高阳为清华叉院助理教授,本科毕业于清华大学计算机系,博士毕业于UC Berkeley。博士导师是Vision领域的大牛Trevor Darrell,读博期间和Sergey Levine合作开始强化学习方面的探索,博后跟随Pieter Abbeel做强化学习&am…...
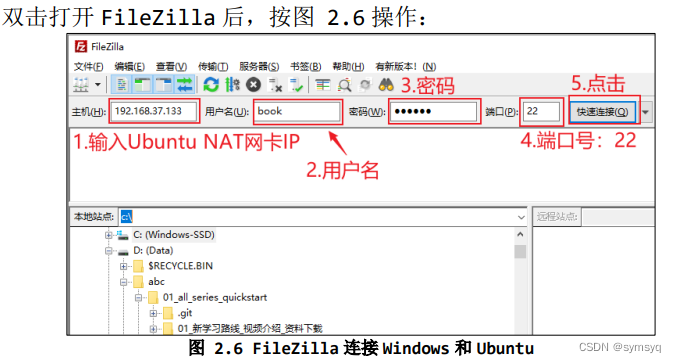
使用 FileZilla 在 Windows 和 Ubuntu 之间传文件
网线一端插在板子的WAN口上,另一段插在电脑上,然后要配一下板子的IP。 板侧: 使用串口链接板子与PC端; 输入指令 ifconfig eth0(具体看wan口对应哪一个) 192.168.1.99 PC端配置: 打开网络设…...

【C++初阶】—— 类和对象 (上)
📝个人主页🌹:EterNity_TiMe_ ⏩收录专栏⏪:C “ 登神长阶 ” 🌹🌹期待您的关注 🌹🌹 类和对象 1. 初步认识C2. 类的引入3. 类的定义声明和定义全部放在类体中声明和定义分开存放 4.…...
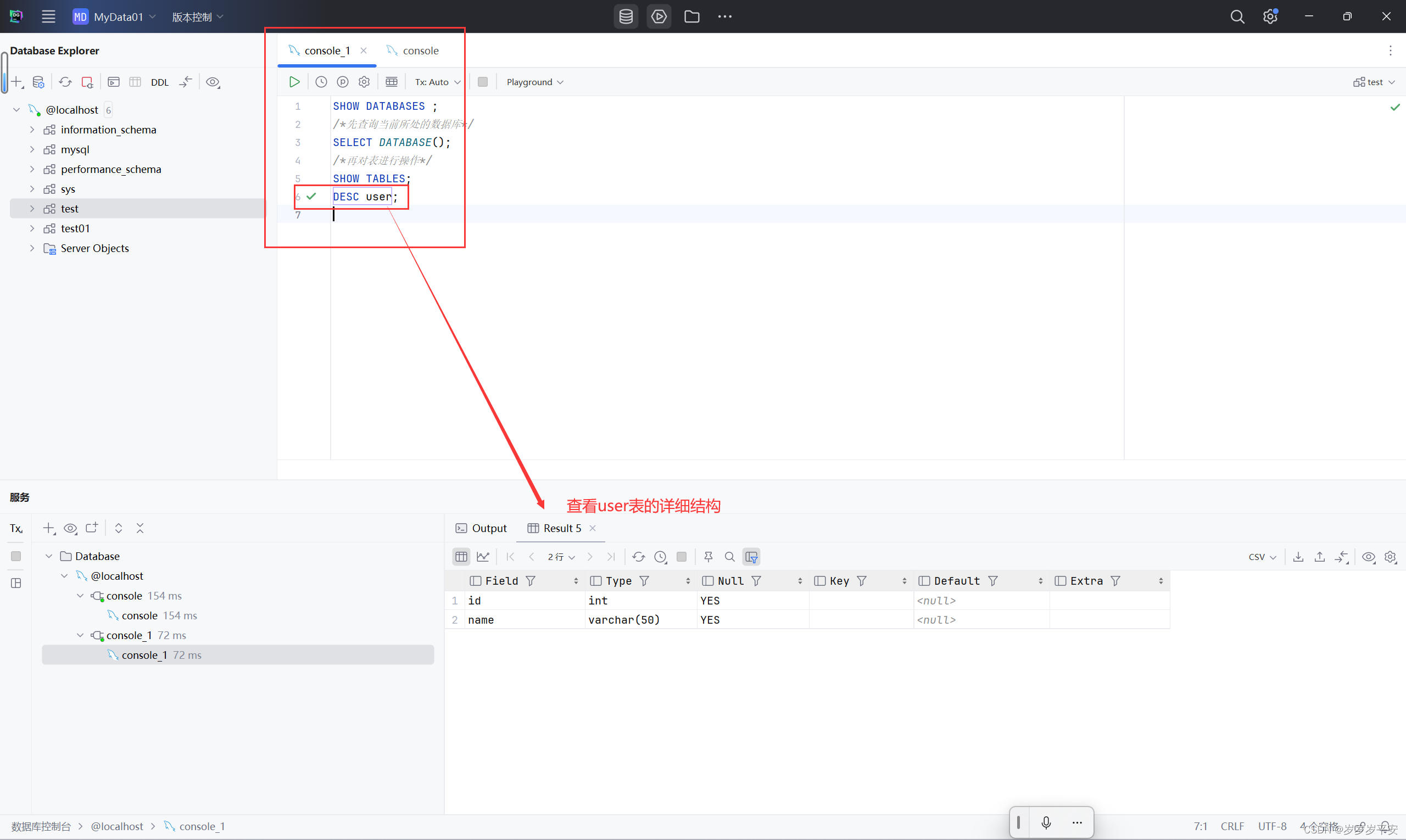
基础—SQL—图形化界面工具的DataGrip使用(2)
一、回顾与引言 (1) 上次内容,博客讲到了DDL语句的数据库操作、表操作、表字段的操作的相关语法,然而之前都是在MySQL的命令行当中去操作演示的。这种方式可以用,但是使用的话,第一,在我们日常…...

4-主窗口
4-主窗口 1、简介2 菜单栏、工具栏、状态栏2.1 菜单栏2.2 QAction2.3 工具栏2.4 状态栏 3 混合方式UI设计 1、简介 QMainWindow是一个为用户提供主窗口程序的类,包含一个菜单栏、多个工具栏、多个停靠控件、一个状态栏以及一个中心控件,是许多应用程序&…...

四川景源畅信:抖音小店新手如何做?
随着短视频平台的兴起,抖音小店成为了许多创业者的新选择。但是,对于新手来说,如何在抖音上开设并经营好自己的小店呢?本文将围绕这一问题展开讨论。 一、明确目标和定位作为抖音小店的新手,首先要明确自己的经营目标和定位。是想…...

EventSource
什么是EventSource EventSource 是一个用于服务器推送事件(Server-Sent Events, SSE)的接口,它允许服务器推送实时更新到浏览器。与 WebSocket 不同,SSE 是单向的(服务器到客户端),适用于更新频…...

Vue2 Element-UI 分页组件el-pagination 修改 自带的total、跳转等默认文字
场景需求: Vue2 Element-UI 分页组件el-pagination 修改 自带的total、跳转等默认文字。如下图:默认提示字变成了英文,如何将其 变成 汉字提示呢? 解决方案: 1.方案1:修改DOM内容 不提倡此方案…...

【简单介绍下线性回归模型】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共…...
有限元法之有限元空间的构造
目录 一、区域Ω的剖分 二、三角形一次元 三、一次元的基函数与面积坐标 四、三角形二次元及其基函数 前两节我们介绍了有限元基本概念和变分理论的推导,本节我们继续探讨有限元空间的构造。 一、区域Ω的剖分 对矩形区域进行三角剖分,其中x方向剖…...

高通车规芯片分析
高通三款芯片 SA8155P 7nm SA8295P 5nm SA8255P 5nm 分析AECQ等级 AECQ100里面定义了5个工作环境温度等级:Grade0:-40-150 Grade1:-40-125 Grade2:-40-105 Grade3:-40-85 Grade4:0-70AEC-Q100整体认证测试…...

Flutter 中的 TextButton 小部件:全面指南
Flutter 中的 TextButton 小部件:全面指南 在Flutter的世界里,TextButton是一个基础的小部件,用于创建只包含文本的按钮。它通常用于对话框、表单以及需要强调主要操作的界面。本文将为您提供一个全面的指南,帮助您了解如何使用T…...

通过键值对访问字典
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 在Python中,如果想将字典的内容输出也比较简单,可以直接使用print()函数。例如,要想打印dictionary字典ÿ…...

海外仓扫码管理系统怎么选?精准,高效管理需求才是核心需求
海外仓对那些想拓展国际市场的商家来说还是非常重要的,大部分的货物都需要先运到海外仓,才能继续进行下一步的物流快递发货。 那对于海外仓本身来说,当面临大量订单的时候,怎么快速的管理订单,拣选货物就变得十分重要…...

基于51单片机的智能灯光控制系统
一.硬件方案 智能灯光控制系统由单片机最小系统、人体感应模块、关照强度模块、灯光控制模块、电源模块和灯泡组成。本文以STC89C52单片机为核心,通过利用光照度和红外人体感应相结合主动与被动的探测方法,现了室内无人或者关照充足时灯光自动光灯&…...

测试开发面试题
简述自动化测试的三大等待 强制等待。直接使用time.sleep()方法让程序暂停指定的时间。优点是实现简单,缺点是不够灵活,可能会导致不必要的等待时间浪费。隐式等待。设置一个固定的等待时间,在这个时间内不断尝试去查找元素,如果…...
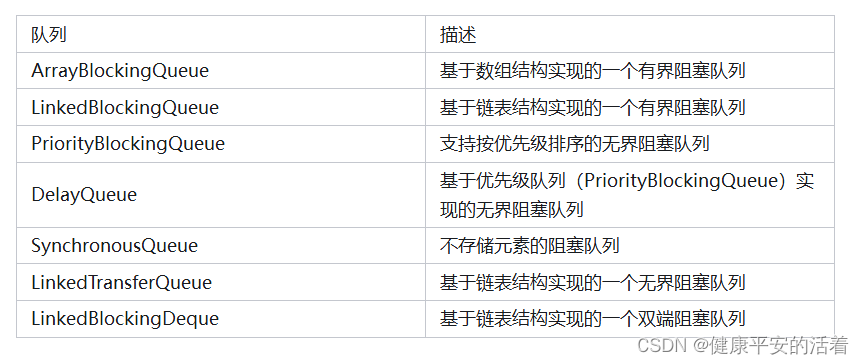
多线程JUC 第2季 BlockingQueue 阻塞队列
一 阻塞队列 1.1 阻塞队列介绍 阻塞队列(BlockingQueue)是一个在队列基础上又支持了两个附加操作的队列: put方法:当队列装满时,添加的线程则被阻塞,直到队列不满,则可用。 take方法&#x…...
-带查询扩展的全文搜索)
【MySQL精通之路】全文搜索(3)-带查询扩展的全文搜索
博主PS:你可以把他理解为,查询猜测,膨胀查询,查询的第六感。 全文搜索支持查询扩展(尤其是其变体“盲查询扩展”)。 当搜索短语太短时,这通常很有用,这通常意味着用户依赖于全文搜索…...
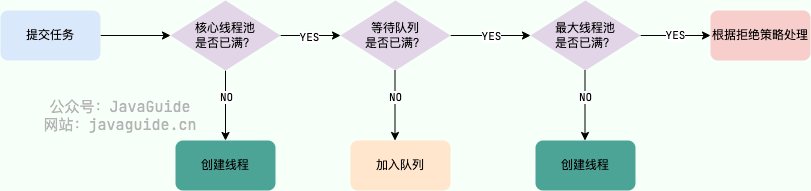
【面试必看】Java并发
并发 1. 线程 1. 线程vs进程 进程是程序的一次执行过程,是系统运行程序的基本单位,因此进程是动态的。 系统运行一个程序即是一个进程从创建,运行到消亡的过程。在 Java 中,当我们启动 main 函数时其实就是启动了一个 JVM 的进…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...



