大数据开发面试题【数仓篇】
197、数据仓库和传统数据库区别
由于历史数据使用频率过低,导致数据堆积,查询性能下降;用于查询分析,涉及大量的历史数据,数据仓库中的数据一般来日志文件和事务
数据库是跟业务挂钩的,数据库不可能装下一个公司所有的数据,因此数据库的是个设计通常只针对一个应用而设计的;数据仓库是依照分析需求、分析维度、分析指标进行设计的
数据库的操作一般是OLTP:是针对具体的业务在数据库中的联机操作;数据仓库的操作一般是OLAP,是针对某些主题的里哦是数据进行分析,支持管理决策
数据库中主要存放的是一些在线的数据,数仓中主要存放的是历史数据,并且存放的数据要比数据库多
数据库中主要用于处理业务,数仓中主要用于数据分析
数据库的设计就是避免冗余,数仓中会专门引入冗余,减少后面进行的大量的join操作
补充:数仓是什么
数仓是一个面向主题的、集成的(来自不同的数据源)、非易失(一般不会进行删除和修改)并且随时间变化(数据不会变,而是数据随着时间会不断增多)的数据集合,主要用于存储历史数据,然后通过分析整理进而提供数据支持和辅助决策
198、数仓为什么要分层
在管理数据的时候,能对数据有一个更加清晰的掌控
优点:清晰的数据结构;数据血缘追踪;减少重复开发;把复杂的问题简单化;屏蔽原始数据的异常影响
ODS:原始数据层,直接接入业务库、埋点日志、消息队列等,是数仓的准备区
DWD:数据细节层,业务层和数据仓库层的隔离层,保持和ODS层相同颗粒度,进行数据清洗和规范化操作,去空、脏数据
DWM:数据中间层:在DWD基础之上进行轻微的聚合操作,计算出相应的统计指标,聚合结果会生成中间表
DWS:数据服务层:在DWM基础上,整合汇总成一个主题的数据服务层,汇总结果是宽表
ADS:数据应用层:供数据分析和挖掘使用,用于报表
199、数仓建模常用模型吗?区别、优缺点?
三范式建模(immon):在数据仓库的逻辑需要从业务系统的数据模型中的逻辑模型中抽象实体,实体的属性,实体的子类,实体的关系等
范式建模最大的优点是从关系型数据库的角度出发,结合了业务系统的数据模型,能够实现数据仓库的建模;但是这种方法只是限定在关系型数据库之上,限制了整个数据仓库模型的灵活性
维度建模(Kimball):按照事实表、维度表来构建数据仓库、数据集市,星型模型应运而生
维度建模步骤:
1、选择业务过程
2、声明粒度:在同一张事实表中,必须具有相同的粒度,不同的粒度数据建立不同的事实表,一般从最细的粒度开始设计,
3、确认维度:维度表是业务分析的入口,维度表中不能出现重复数据,应该使主键唯一
4、确认事实:事实表是用来度量的,事实表中每一行对应一个度量,每行中的数据是一个特定级别的细节数据;维度建模的核心原则之一就是同一事实表的所有度量必须具有相同粒度
补充:星型模型和雪花模型
雪花模型去除了冗余,设计复杂,可读性差,关联的维表很多,查询效率很低,但扩展性好;多个维表没有和事实表直接相连,而是通过其他的维度表,间接的连接在事实表上,
星型模型冗余度高,设计简单,可读性高,关联的维表很少,查询效率高,可扩展性低;当所有的维表都是和事实表直接相连的时候,整个图形看上去就是一个星星,不存在渐变维度,所以一定有数据冗余,不需要和外表进行关联进行查询和分析,因此效率高
区别:
星型模型和雪花模型最根本的区别就是维度表是直接连接到事实表还是其他维表上
星型模型的数据冗余所以很多查询统计不需要做外部连接
雪花模型遵从三范式,去掉了冗余,有些统计过程需要通过表才可以产生
补充:数仓具体实施步骤
1、进行业务调研:需要了解业务系统,收集分析师运营人员对数据或者报表的需求
2、数据域划分:数据域是指面向业务分析,将业务过程或者维度进行抽象的集合
3、构建总线矩阵:明确业务过程所属的数据域,明确业务过程域与维度的关系
4、规范定义:定义指标(原子指标、派生指标)
5、明细模型设计:包括DIM和DWD
6、汇总模型设计:DWS和ADS
7、代码开发和运维监控
200、维度表和事实表的区别?
维度表是对数据进行分析时候所用的一个量
事实表:是数据聚合后依据某个维度生成的结果表,是具体的统计表
举例:销售统计表一个事实表;价格表和销量表是一个维度表
事实表用来存储事实的度量以及指向各个维的外键值,维表用来保存该维的元数据
补充:缓慢变化维
一些维度表的数据不是静态的,而是会随着事件而缓慢变化
SCD的解决方案:
拉链表:数据仓库系统的目标之一就是正确地表示历史记录,典型代表就是拉链表,保留历史的数据,并插入新的数据
拉链表不存储冗余的数据,只有某行的数据发生变化,才需要保存下来,相比每次全量同步会节省很多空间
201、OLTP和OLAP
oltp:联机事务处理,是传统的关系型数据库的主要应用,是基本的、日常的事务处理
olap:是联机分析处理,强调数据分析,数据一般来自数仓,用于数据挖掘、BI、复杂计算以及财务分析
202、增量表、全量表和拉链表
增量表记录根本更新周期内的新增的数据,在原表的基础之上新增本周期产生的数据
全量表:记录更新周期内的全量数据,
拉链表:记录数据的历史数据,记录数据从开始一致到当前辩护的所有信息,一般有结束之间和开始时间,如果发生变化,就修改当前数据䣌结束时间
203、数据同样存在 hdfs,为什么 hbase 支持在线查询
1)HBase的存储机制:首先,HBase的机制是数据先写入到内存中,当数据量达到一定的量, 再写入磁盘中, 在内存中,是不进行数据的更新或合并操作的,只增加数据,这使得用户的写操作只要进入内存中就可以立即返回,保证了HBase I/O的高性能。
其次,在内存中的数据是有序的,如果内存空间满了,会刷写到HFile中,而在HFile中保存的内容也是有序的。HFile文件为磁盘顺序读取做了优化,按页存储。是顺序写入而不是随机写入,所以速度很稳定,这样保持稳定的同时,加快了速度。
2)HBase底层架构:HBase底层是LSM-Tree+ HTable(Region分区) + Cache——客户端可以直接定位到要查数据所在的HRegion Server服务器,然后直接在服务器的一个Region上查找要匹配的数据,并且这些数据部分是经过Cache缓存的。
3)HBase的读取读取速度快是因为它使用了LSM树型结构。磁盘的顺序读取速度很快。HBase的存储结构导致它需要磁盘寻道时间在可预测范围内,而关系型数据库,即使有索引,也无法确定磁盘寻道次数。而且,HBase读取首先会在缓存中查找,它采用了LRU(最近最少使用算法),如果缓存中没找到,会从内存中的MemStore中查找,只有这两个地方都找不到时,才会加载HFile中的内容,而我们也提到读取HFile速度会很快,因为节省了寻道开销。
(3) 问题扩展HBase的概念和特点可做扩展回答,再根据特点去回答优劣和核心功能,再延伸到适用场景。
- HBase概念:HBase是建立在HDFS之上,提供高可靠性的列存储,实时读写的数据库系统。它介于Nosql和关系型数据库之间,仅通过主键和主键的Range来检索数据,仅支持单行事务。主要用来存储非结构化和半结构化的松散数据。
- HBase的优缺点:优点:高容错性,高扩展性。key/value存储方式面对海量数据也不会导致查询性能下降。相对于传统行式数据库,在单张表字段很多的时候,可以将相同的列存到不同的服务实例上,分散负载压力。缺点:架构设计复杂,且使用HDFS作为分布式存储,所以在存储少量数据时,它也不会很快。HBase不支持表关联操作,数据分析是HBase的弱项。HBase只部分支持ACID,只支持单行单次操作的事务。
(4) 综合项目中使用清楚HBase和其他数据库的区别,清楚HBase优势劣势,在哪种场景下,使用哪种技术,当所存储数据需要快速插入查询时,使用HBase,所以Storm或Sparksteaming常常存储入HBase。当数据需要大量聚合运算,计算分析结果时,使用Hive存储,所以Hive是数仓,etl的常用工具。
相关文章:

大数据开发面试题【数仓篇】
197、数据仓库和传统数据库区别 由于历史数据使用频率过低,导致数据堆积,查询性能下降;用于查询分析,涉及大量的历史数据,数据仓库中的数据一般来日志文件和事务 数据库是跟业务挂钩的,数据库不可能装下一…...

Leetcode刷题笔记5
76. 最小覆盖子串 76. 最小覆盖子串 - 力扣(LeetCode) 解法一: 暴力枚举 哈希表 先定义left和right,可以在随机位置 枚举一个位置向后找,找到一个位置之后,发现这段区间是一个最小的区间之后,…...

【Qt】Qt中的信号槽
一、信号和槽概述 信号槽是Qt矿建引以为豪的机制之一。 所谓信号槽,实际上就是观察者模式(发布——订阅模式)。当某个事件发生之后,比如,按钮检测到自己被点击了一下,它就会发出一个信号。这种发出的信号是…...

VsCode个人插件
Auto Rename Tag > 同时修改标签 Rainbow Brackets > 不同层级不同括号颜色 Dracula Official > 个人比较喜欢的一款主题 Error Lens > 错误信息显示 ES7REACT/Redux/React-Native>react开发插件 ESLINT Indenticator>方便看结构 Prettier Formatter …...
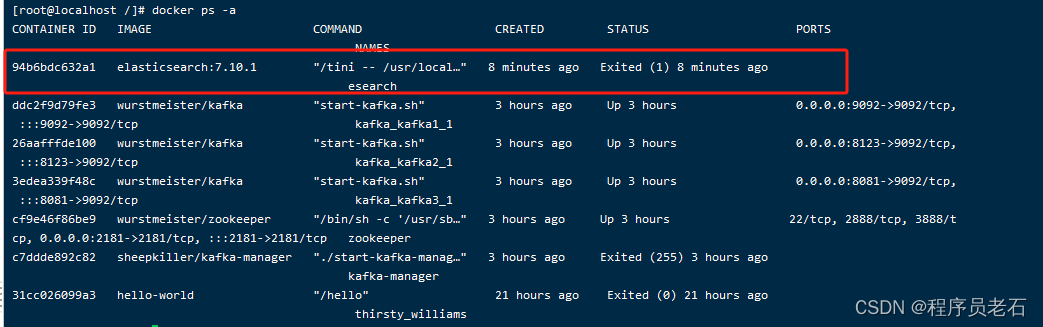
Docker环境安装并使用Elasticsearch
1、拉取es docker pull elasticsearch:7.10.12、查看镜像 docker images3、启动es docker run -d --name esearch -p 9200:9200 -p 9300:9300 elasticsearch:7.10.14、如果启动ES时出现一下问题 Unable to find image docker.elastic.co/elasticsearch/elasticsearch:7.10.…...
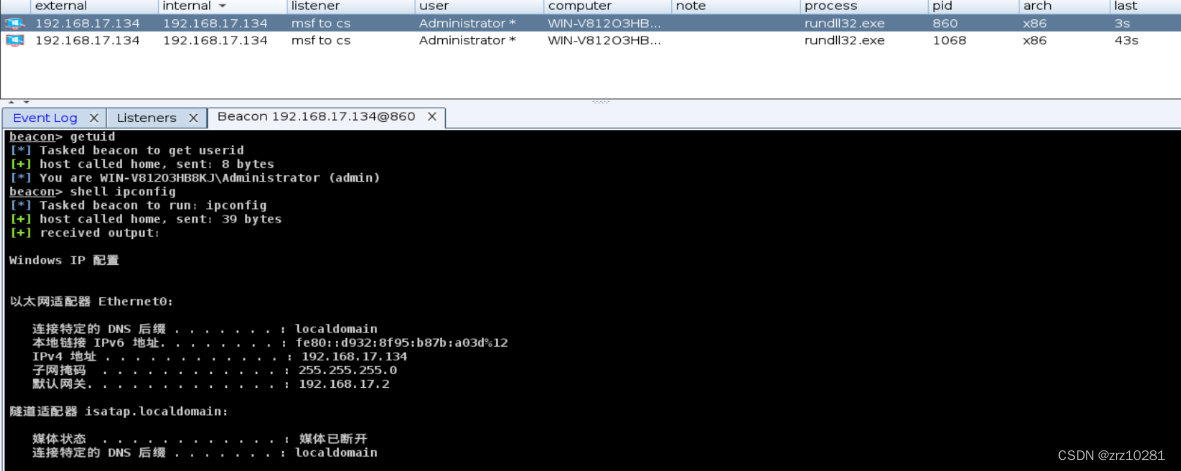
中心渗透Ⅱ
cs与msf权限传递以及mimikatz抓取win2012明文密码 使用Cobalt Strike抓取win2012明文密码,将会话传递到Metasploit Framework上 1.cs生成木马并使目标服务器中马 建立监听生成木马 2.抓取目标主机的明文密码 通过修改注册表来让Wdigest Auth保存明文口令 shell …...
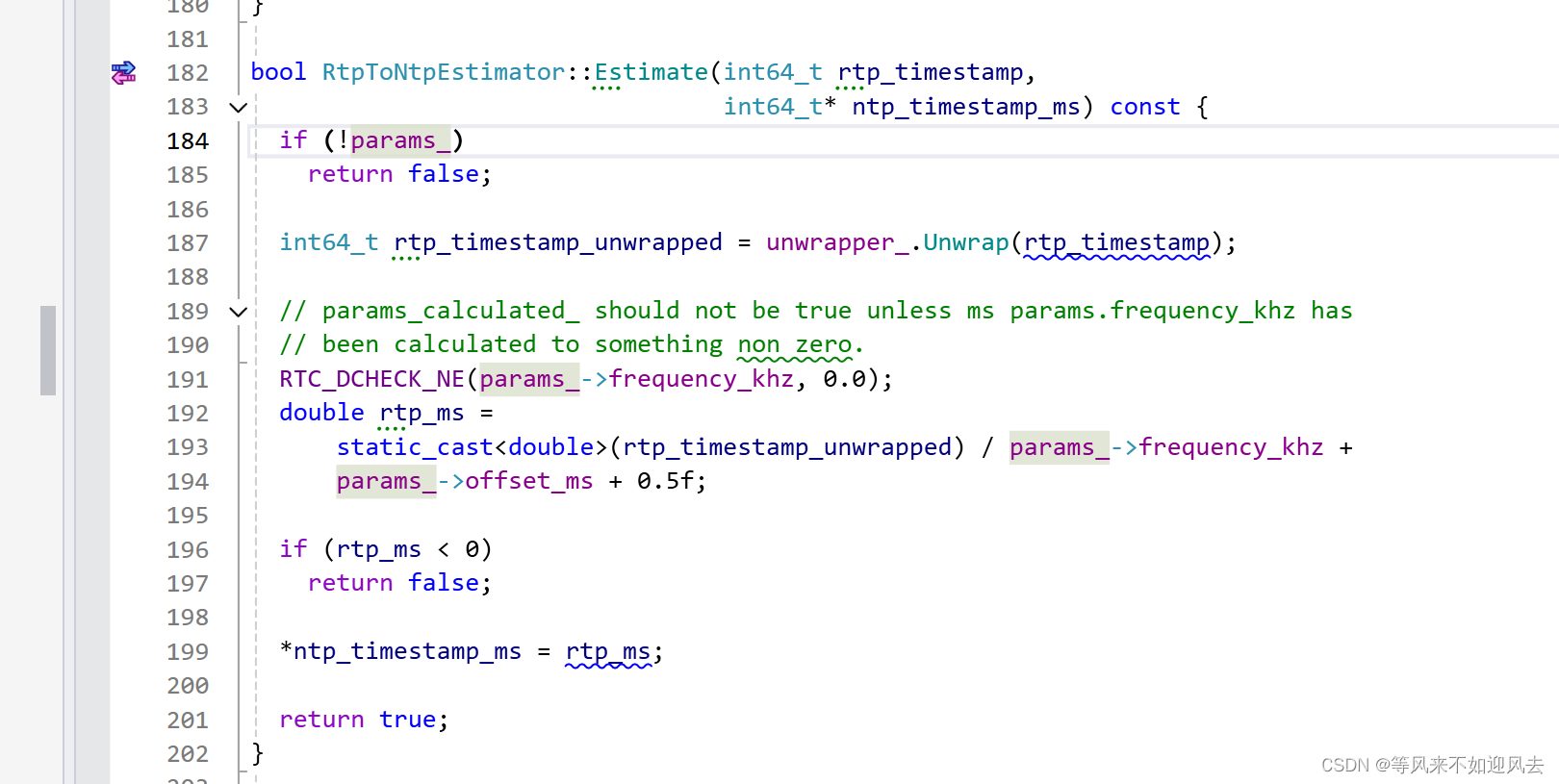
【webrtc】RtpToNtpEstimator:最小二乘法、ntp估计及c++实例
上一篇: 【webrtc】RtpToNtpEstimator:将 RTP 时间戳映射到 NTP 时间 分析了最小二乘法的实现及对rtp到ntp的映射计算的调用流程 基于最小二乘法进行估计 RtpToNtpEstimator::Estimate G:\CDN\rtcCli\m98\src\system_wrappers\source\rtp_to_ntp_estimator.cc RtpToNtpEstima…...
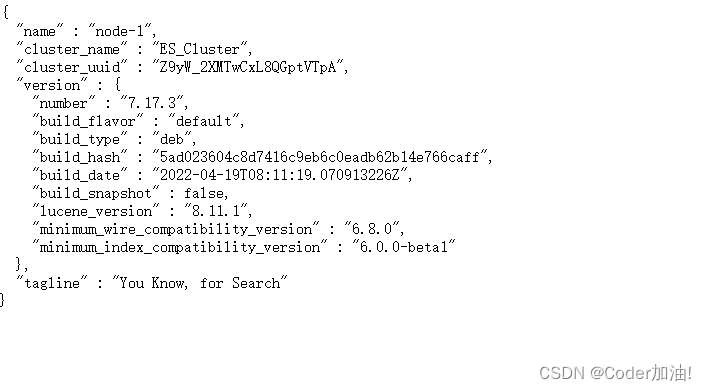
【DevOps】Elasticsearch在Ubuntu 20.04上的安装与配置:详细指南
目录 一、ES 简介 1、核心概念 2、工作原理 3、 优势 二、ES 在 Ubuntu 20.04 上的安装 1、安装 Java 2、下载 ES 安装包 3、创建 ES 用户 4 、解压安装包 5、 配置 ES 6、 启动 ES 7、验证安装 三、ES 常用命令 1、创建索引 2、 插入文档 3、查询文档 四、ES…...
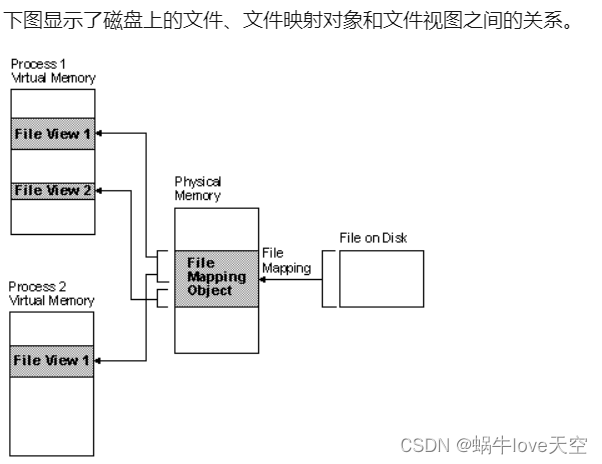
windows内存管理
一 windows系统的内存管理涉及哪些 1.1 虚拟内存管理机制 windows操作系统使用虚拟内存技术,将磁盘文件,通过映射对象(存储在物理内存)关联,映射到虚拟内存作为文件试图。即用户操作"虚拟内存中File View Objec…...
c++ 将指针转换为 void* 后,转换为怎么判断原指针类型?
当将指针转换为void后,擦除了指针所指向对象的类型信息,因此无法通过void指针来判断原始指针的类型。我这里有一套编程入门教程,不仅包含了详细的视频讲解,项目实战。如果你渴望学习编程,不妨点个关注,给个…...

Swift 属性
属性 一、存储属性1、常量结构体实例的存储属性2、延时加载存储属性3、存储属性和实例变量 二、计算属性1、简化 Setter 声明2、简化 Getter 声明3、只读计算属性 三、属性观察器四、属性包装器1、设置被包装属性的初始值2、从属性包装器中呈现一个值 五、全局变量和局部变量六…...

基于maxkey接入jeecgboot并实现账户同步
1. 注册应用 1.1 在统一认证中心注册第三方应用 1.1.1 填写应用名和登录地址 1.1.2 填写认证地址授权方式和作用域 1.1.3 选择权限范围并提交 1.2 配置访问权限 1.2.1 指定用户组 1.1.2 选择注册的应用 1.1.3 在单点登录认证页面查看添加的应用 1.3 同步一个第三方应用的账号…...

kafka Kerberos集群环境部署验证
背景 公司需要对kafka环境进行安全验证,目前考虑到的方案有Kerberos和SSL和SASL_SSL,最终考虑到安全和功能的丰富度,我们最终选择了SASL_SSL方案。处于知识积累的角度,记录一下kafka keberos安装部署的步骤。 机器规划 目前测试环境公搭建了三台kafka主机服务,现在将详细…...
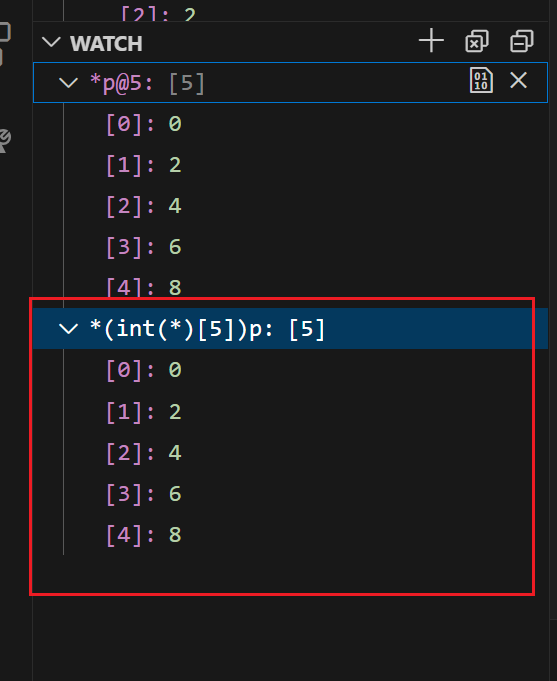
[C++]debug介绍+debug时如何查看指针指向内存处的值
一、简介 预备工具和知识:使用使用VSCode使用Debug。 本文简介:本文将简要介绍debug中Continue,Step Over,Step Into和Restart的功能。并介绍如何在debug时查看动态内存地址(指针)的值; 二、D…...

AI学习指南数学工具篇-凸优化在支持逻辑回归中的应用
AI学习指南数学工具篇-凸优化在支持逻辑回归中的应用 一、引言 在人工智能领域,逻辑回归是一种常见的分类算法,它通过学习样本数据的特征和标签之间的关系,来进行分类预测。而在逻辑回归算法中,凸优化是一种重要的数学工具&…...

Flutter 中的 AspectRatio 小部件:全面指南
Flutter 中的 AspectRatio 小部件:全面指南 Flutter 是一个流行的跨平台 UI 框架,它提供了丰富的小部件来帮助开发者构建高质量的应用程序。在 Flutter 的小部件库中,AspectRatio 是一个非常有用的小部件,它允许开发者以一种简单…...

应用程序中的会话管理和Cookie安全指南
应用程序中的会话管理和Cookie安全指南 在现代应用程序中,会话管理和Cookie安全是确保用户信息和数据安全的重要组成部分。本文将详细介绍会话管理的最佳实践以及如何通过安全的Cookie设置来保护会话ID的交换。 单点登录(SSO)及会话管理机制…...

备战秋招c++ 【持续更新】
T1 牛牛的快递 原题链接:牛牛的快递_牛客题霸_牛客网 (nowcoder.com) 题目类型:模拟 审题&确定思路: 1、超过1kg和不足1kg有两种不同收费方案 ---- 起步价问题 2、超出部分不足1kg的按1kg计算 ----- 向上取整 3、向上取整的实现思路…...

整数拆分~
way:process //上一个拆出来的数是pre //还剩下rest需要去拆 //返回拆解的方法数 #include<iostream> using namespace std;//上一个拆出来的数是pre //还剩下rest需要去拆 //返回拆解的方法数 int process(int pre, int rest) {if(rest0) return 1;//因为后…...
【Qt Creator】跨平台的C++图形用户界面应用程序开发框架---QT
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 1.互联网的核心岗位以及职…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
