Prime算法构造最小生成树(加点法)
一、算法逻辑
想要轻松形象理解Prime的算法逻辑,视频肯定比图文好。
小编看过很多求相关的教学视频,这里选出一个我认为最好理解的这一款安利给大家。
因为他不仅讲解细致,而且还配合了动画演示,可以说把一个抽象的东西讲的非常的形象了。
B站链接:【图-最小生成树-Prim(普里姆)算法】
接下来,小编会对视频中的算法补充一个java的具体实现
二、java实现
只用一个接口,写的代码,肯定不好理解,因为涉及到图的操作,所以这里先给一下基本的图的代码(使用邻接矩阵):
class Constant {public static final int MAX=Integer.MAX_VALUE;
}public class GraphByMatrix {private char[] arrayV;//顶点数组private int[][] matrix;//矩阵,存放每一个边的权重private boolean isDirect;//是否是有向图/*** 构造方法** @param size 代表当前顶点的个数* @param isDirect 是否是有向图,true是有向图*/public GraphByMatrix(int size, boolean isDirect) {this.arrayV = new char[size];//顶点的个数是sizematrix = new int[size][size];for (int i = 0; i < size; i++) {Arrays.fill(matrix[i], Constant.MAX);}this.isDirect = isDirect;}/*** @param srcV 起点* @param destV 终点* @param weight 权值*/public void addEdge(char srcV, char destV, int weight) {//重载之一,用来建立普通图int srcIndex = getIndexOfV(srcV);int destIndex = getIndexOfV(destV);matrix[srcIndex][destIndex] = weight;//如果是无向图 那么相反的位置 也同样需要置为空if (!isDirect) {matrix[destIndex][srcIndex] = weight;}}/*** @param srcIndex 起点* @param desIndex 终点* @param weight 权重*/public void addEdge(int srcIndex, int desIndex, int weight) {//重载两个之一,用来建立最小生成树matrix[srcIndex][desIndex] = weight;//如果是无向图 那么相反的位置 也同样需要置为空if (!isDirect) {matrix[desIndex][srcIndex] = weight;}}/*** 获取顶点V的下标** @param v* @return*/private int getIndexOfV(char v) {for (int i = 0; i < arrayV.length; i++) {if (arrayV[i] == v) {return i;}}return -1;}/*** 定义了一个边的抽象类* 用来存储边的*/static class Edge {public int srcIndex;public int destIndex;public int weight;//权重public Edge(int srcIndex, int destIndex, int weight) {this.srcIndex = srcIndex;this.destIndex = destIndex;this.weight = weight;}}public static void main(String[] args) {}
}了解了上面的代码,看这个普利姆算法的接口就容易了:
/*** 普利姆算法* 最小生成树** @param minTree 要生成的树* @param V 选择的一个顶点*/public int prim(GraphByMatrix minTree, char V) {//需要先给一个顶点,作为起点int indexSrc = getIndexOfV(V);//获取起始顶点的下标/** 把顶点分成两个集合* 第一个集合存储已经确定好是minTree的一个顶点* 第二个存储还未确定的顶点** */int n = arrayV.length;//存的值,就是顶点的下标Set<Integer> setX = new HashSet<>(n);//长度就是所有顶点的大小,用来存确定的顶点Set<Integer> setY = new HashSet<>(n);//用来存还没有确定的顶点setX.add(indexSrc);//起始顶点已经是确定好了的,所以直接放到setX这个集合中//接下来,把除了起始顶点外的其他顶点都放到setY这个集合中(也就是还未确定的顶点)for (int i = 0; i < n; i++) {if (i != indexSrc) setY.add(i);}/** 定义一个优先级队列(小根堆,因为有得到最小权值),用来存储还没有确定好的 从确定顶点到没有确定顶点的边*/PriorityQueue<Edge> minHeap = new PriorityQueue<>((o1, o2) -> o1.weight - o2.weight);//默认是建立小根堆(因为是自定义类型,要重写compareTo)//接下来把从起始顶点 连接 到其他顶点的边都放到优先级队列中for (int i = 0; i < n; i++) {if (matrix[indexSrc][i] != Constant.MAX) {//从起始顶点->另一个没有确定的顶点存在(等于MAX代表不存在),就放到队列minHeap.offer(new Edge(indexSrc, i, matrix[indexSrc][i]));}}int totalWeight = 0;//用来记录总的权值int edgeN = 0;//用来记录已经确定的边while (edgeN != n - 1 && !minHeap.isEmpty()) {//只要没有加边到最小生成树,并且队列没有空,就一直加边//出队一个元素Edge edge = minHeap.poll();//判断这个边的 目标顶点 是否 在setX(已经确定的顶点)中if (!setX.contains(edge.destIndex)) {//如果不在,那么把这个边,放到最小生成树中//放到最小生成树minTree.addEdge(edge.srcIndex, edge.destIndex, edge.weight);//放完一个边,就记得edgeN++ 更新权重edgeN++;totalWeight += edge.weight;//记住把对应的顶点确定setX.add(edge.destIndex);//同时,在setY中删除对应目标顶点setY.remove(edge.destIndex);/** 到了这里,因为已经确定了一个新的顶点,* 因此,还要在这个新的顶点的基础上,* 入队从新顶点指向其他顶点的边* */for (int i = 0; i < n; i++) {if (matrix[edge.destIndex][i] != Constant.MAX && !setX.contains(i)) {//只要有边,并且不会形成环,那么入队minHeap.offer(new Edge(edge.destIndex, i, matrix[edge.destIndex][i]));}}}/*else{如果在setY就不做操作,如果继续放到minTree中,会形成环!!!}*/}if (edgeN == n - 1) return totalWeight;elsereturn -1;//没有找到,返回-1}
相关文章:
)
Prime算法构造最小生成树(加点法)
一、算法逻辑 想要轻松形象理解Prime的算法逻辑,视频肯定比图文好。 小编看过很多求相关的教学视频,这里选出一个我认为最好理解的这一款安利给大家。 因为他不仅讲解细致,而且还配合了动画演示,可以说把一个抽象的东西讲的非常…...

【VTKExamples::Utilities】第五期 CommandSubclass
很高兴在雪易的CSDN遇见你 VTK技术爱好者 QQ:870202403 公众号:VTK忠粉 前言 本文分享VTK样例CommandSubclass,希望对各位小伙伴有所帮助! 感谢各位小伙伴的点赞+关注,小易会继续努力分享,一起进步! 你的点赞就是我的动力(^U^)ノ~YO 1. CommandSubclass …...
重生之 SpringBoot3 入门保姆级学习(04、 包扫描)
重生之 SpringBoot3 入门保姆级学习(04、 包扫描) 2.1 包扫描 2.1 包扫描 默认包扫描规则: SpringBootApplication 标注的就是主程序 SpringBoot 只会扫描主程序下面的包 自动的 component-scan 功能 在 SpringBootApplication 添加参数可以…...

VectorDBBench在windows的调试
VectorDBBench在windows的调试 VectorDBBench是一款向量数据库基准测试工具,支持milvus、Zilliz Cloud、Elastic Search、Qdrant Cloud、Weaviate Cloud 、 PgVector、PgVectorRS等,可以测试其QPS、时延、recall。 VectorDBBench是一款使用python编写的…...
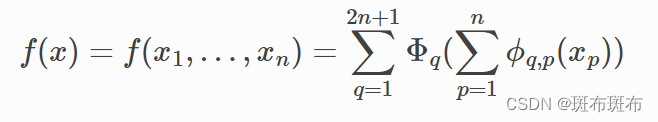
KAN(Kolmogorov-Arnold Network)的理解 1
系列文章目录 第一部分 KAN的理解——数学背景 文章目录 系列文章目录前言KAN背后的数学原理:Kolmogorov-Arnold representation theorem 前言 这里记录我对于KAN的探索过程,每次会尝试理解解释一部分问题。欢迎大家和我一起讨论。 KAN tutorial KAN背…...
)
Vue 项目中使用 Element UI库(Element UI 是一套基于 Vue.js 的桌面端组件库)
1. 安装 Element UI npm install element-plusnext 2.引入 Element UI(在main.js中引入组件,注意要引入.css文件,图标也要单独引用) import { createApp } from vueimport ElementPlus from element-plusimport element-plus/dist/index.css…...
C++240527
定义自己的命名空间 my_sapce,在 my_sapce 中定义 string 类型的变量 s1,再 定义一个函数 完成 对字符串的逆置 。 #include <iostream>//导入 标准命名空间,cout 和 endl 标识符 存在于标准命名空间中 using namespace std;//定义了自…...

揭秘动态网页爬取:步骤与实战技巧
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一、引言 二、动态网页爬取步骤 三、实战技巧分享 四、总结 一、引言 在大数据时代&#…...

Lvm逻辑卷调整容量
1、拉伸逻辑卷调整容量 [rootdesktop ~]# df ‐hT Filesystem Type Size Used Avail Use% Mounted on /dev/sda1 xfs 9.8G 3.3G 6.5G 34% / devtmpfs devtmpfs 660M 0 660M 0% /dev tmpfs tmpfs 674M 0 674M 0% /dev/shm tmpfs tmpfs 674M 8.9M 666M 2% /run tmpfs tmpfs 674M …...
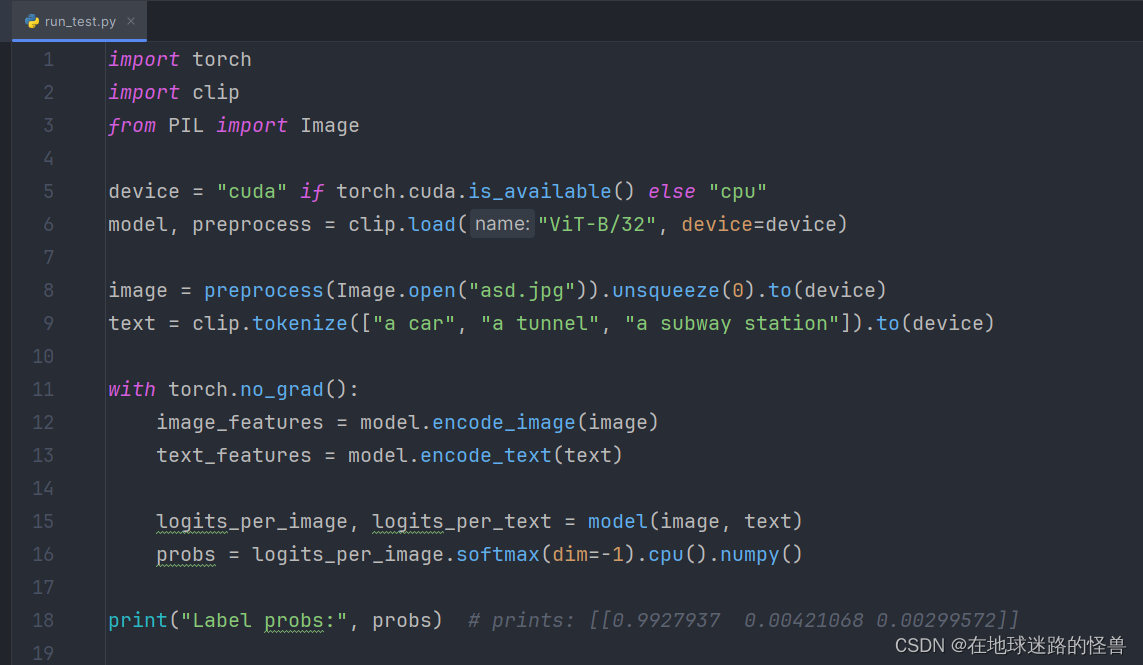
CLIP源码详解:clip.py 文件
前言 这是关于 CLIP 源码中的 clip.py 文件中的代码带注释版本。 clip.py 文件的作用:封装了 clip 项目的相关 API,通过这些 API ,我们可以轻松使用 CLIP 项目预训练好的模型进行自己项目的应用。 另外不太容易懂的地方都使用了二级标题强…...

linux下重启oracle数据库步骤
Linux下重启oracle数据库步骤: 1.使用oracle用户登录数据库服务器(root登录的话进入数据库时会找不到sqlplus命令) su – oracle 2.通过数据库管理员sysdba进入oracle数据库 sqlplus / as sysdba 3.关闭数据库 shutdown immediate ࿰…...

[自动驾驶技术]-1 概述技术和法规
自动驾驶(Autonomous Driving),也称为无人驾驶或自驾,是指通过计算机系统和传感器设备,自动驾驶汽车在没有人类干预的情况下能够感知环境并做出驾驶决策,从而实现车辆的自主行驶。 自动驾驶技术层级 自动…...
Qt自定义标题栏
效果如下: 代码如下: // widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr…...

java如何向数组中插入元素
java的数组是不可改变的,因此如果要向数组中插入新的元素,需要新建一个数组,新的数组元素个数减去老数组元素个数的差大于等于要插入新的元素数量。 假如说要插入一个数组元素,需要把新元素插入到中间,把新的数组分为…...

4、PHP的xml注入漏洞(xxe)
青少年ctf:PHP的XXE 1、打开网页是一个PHP版本页面 2、CTRLf搜索xml,发现2.8.0版本,含有xml漏洞 3、bp抓包 4、使用代码出发bug GET /simplexml_load_string.php HTTP/1.1 补充: <?xml version"1.0" encoding&quo…...
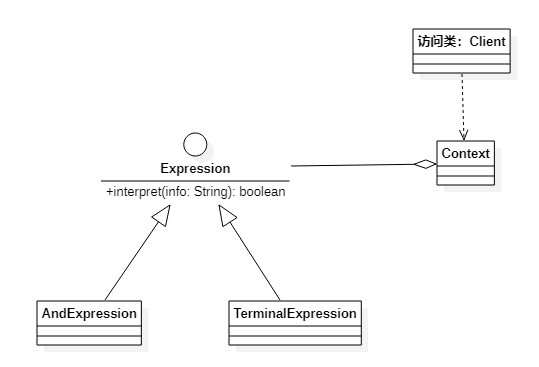
设计模式-解释器模式
作者持续关注 WPS二次开发专题系列,持续为大家带来更多有价值的WPS开发技术细节,如果能够帮助到您,请帮忙来个一键三连,更多问题请联系我(QQ:250325397) 定义 解释器模式(Interpreter Pattern&…...
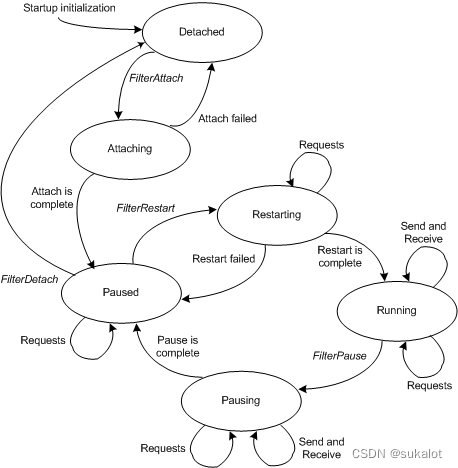
NDIS驱动程序堆栈
NDIS 6.0 引入了暂停和重启驱动程序堆栈的功能。 若要支持 NDIS 6.0 提供的堆栈管理功能,必须重写旧版驱动程序。 NDIS 6.0 还引入了 NDIS Filter驱动程序。 Filter驱动程序可以监视和修改协议驱动程序与微型端口驱动程序之间的交互。 与 NDIS 5 相比,F…...

大数据开发面试题【数仓篇】
197、数据仓库和传统数据库区别 由于历史数据使用频率过低,导致数据堆积,查询性能下降;用于查询分析,涉及大量的历史数据,数据仓库中的数据一般来日志文件和事务 数据库是跟业务挂钩的,数据库不可能装下一…...

Leetcode刷题笔记5
76. 最小覆盖子串 76. 最小覆盖子串 - 力扣(LeetCode) 解法一: 暴力枚举 哈希表 先定义left和right,可以在随机位置 枚举一个位置向后找,找到一个位置之后,发现这段区间是一个最小的区间之后,…...

【Qt】Qt中的信号槽
一、信号和槽概述 信号槽是Qt矿建引以为豪的机制之一。 所谓信号槽,实际上就是观察者模式(发布——订阅模式)。当某个事件发生之后,比如,按钮检测到自己被点击了一下,它就会发出一个信号。这种发出的信号是…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
