Kalman Filter in SLAM (6) ——Error-state Kalman Filter (EsKF, 误差状态卡尔曼滤波)

文章目录
- 0.前言
- 1. IMU的误差状态空间方程
- 2. 误差状态观测方程
- 3. 误差状态卡尔曼滤波
- 4. 误差状态卡尔曼滤波方程细节问题
0.前言
这里先说一句:什么误差状态卡尔曼?完全就是在扯淡!
回想上面我们推导的IMU的误差状态空间方程,其实如果后面我们是使用优化的方法,而不是使用滤波的方法,那么推导完IMU的误差状态空间方程就可以了。因为上面我们已经说了,IMU的误差状态空间方程和状态空间方程的协方差矩阵是完全一致的。所以后面如果是使用优化的方法,那么就可以使用误差状态空间方程得到的协方差矩阵作为IMU积分值的置信度了。
但是如果我们是要使用滤波的方法呢?那么就要使用基于误差状态(而非状态)的卡尔曼滤波了,也就是我们这里说的误差状态卡尔曼滤波。
这里可能有一个疑问,既然我们推导的误差状态和状态的协方差矩阵是相等的,那直接用普通的那种基于状态变量的卡尔曼滤波不就可以了吗?实际上确实是可以的,经过后面的公式推导也可以发现,误差状态卡尔曼滤波的公式实际上和普通的卡尔曼滤波没有任何区别,所以上面第一句才说“误差状态卡尔曼完全就是在扯淡”!
但是为什么还要用它呢?实际上只有一个原因,就是 旋转的原因,前面我们说了旋转的状态变量我们选的是 角轴(旋转向量),但是旋转向量存在一个问题,那就是周期性。所以如果我们用的是 状态旋转向量,那么在滤波过程中就存在周期性。但是如果我们选择的是 误差状态旋转向量 呢?它始终在0附近,所以就 不会产生周期性 的问题。因此实际上使用误差状态卡尔曼滤波完全就是因为这个原因,而且现在仔细想想,实际上误差状态卡尔曼滤波我们 不应该把它理解为一种新的滤波算法(比如 KF 和 EKF 就是两种算法,虽然非常像),它只是在卡尔曼滤波的时候把状态变量从原来的 状态 变成了 误差状态,其他并没有任何变化。
1. IMU的误差状态空间方程
见本系列另一篇博客: Kalman Filter in SLAM (4) ——IMU Intergration and State Space Representation (IMU积分和状态空间表示)
2. 误差状态观测方程
用 z\boldsymbol zz 代表 预测观测值,也就是我们把IMU预测得到的状态(先验状态) x^k\boldsymbol {\hat{x}}_{k}x^k 带入到观测方程中得到的 计算出来的观测值。现在假设我们的先验状态 x^k\boldsymbol {\hat{x}}_{k}x^k 的误差是 δx^k\delta \boldsymbol {\hat{x}}_{k}δx^k。由于它存在误差,导致带入观测方程之后得到的 预测观测值 z\boldsymbol zz 产生的误差是 δz\delta \boldsymbol zδz。利用公式(37),我们带入 真实的状态值 xk=x^k+δx^k\boldsymbol x_{k} =\boldsymbol {\hat{x}}_{k} + \delta \boldsymbol {\hat{x}}_{k}xk=x^k+δx^k 到 函数自变量 xk\boldsymbol x_kxk 中,可以得到真实的状态算出的预测观测值 z+δz\boldsymbol z + \delta \boldsymbol zz+δz 的表达式为:
z+δz=h(x^k,0)+Hk(x^k+δx^k−x^k)+Vkvk\boldsymbol z + \delta \boldsymbol z = \boldsymbol h(\boldsymbol {\hat{x}}_{k}, \boldsymbol 0) + \boldsymbol H_{k} (\boldsymbol {\hat{x}}_{k} + \delta \boldsymbol {\hat{x}}_{k} - \boldsymbol {\hat{x}}_{k}) + \boldsymbol V_{k} \boldsymbol v_{k} z+δz=h(x^k,0)+Hk(x^k+δx^k−x^k)+Vkvk
注意:我们对观测方程进行线性化最主要的目的就是得到系数矩阵 H\boldsymbol HH,但是另外一个同样重要的点就是把状态值带入观测方程计算预测观测值的时候,我们也必须带入 线性化的方程,而不能带入原来的线性化的方程中,这样才能保证我们用的是一个模型。否则就变成了系数矩阵用的线性化模型,而计算的观测值用的是非线性模型。因此公式(39)中我们的自变量只有原来公式(37)中的 xk\boldsymbol x_kxk,误差变量 δxk\delta \boldsymbol x_kδxk 并没有带入到函数 h(x^k,0)\boldsymbol h(\boldsymbol {\hat{x}}_{k}, \boldsymbol 0)h(x^k,0) 中,因为它只是一个线性函数的常数项。
再由公式(38)我们可以发现,z=h(x^k,0)\boldsymbol z = \boldsymbol h(\boldsymbol {\hat{x}}_{k}, \boldsymbol 0)z=h(x^k,0),把这个结果带入到公式(39)中,我们就可以得到 状态误差 δxk\delta \boldsymbol x_kδxk 和 预测观测值的误差 δz\delta \boldsymbol zδz 的关系,即 误差状态观测方程:
δz=Hkδx^k+Vkvk\delta \boldsymbol z = \boldsymbol H_{k} \delta \boldsymbol {\hat{x}}_{k} + \boldsymbol V_{k} \boldsymbol v_{k} δz=Hkδx^k+Vkvk
可见这个公式的结果跟我们推导的IMU误差状态空间方程的结果也是非常相似的,因为 误差观测方程 的系数矩阵和我们的 状态观测方程 的系数矩阵是完全相等的。
3. 误差状态卡尔曼滤波
我们先给出之前已经推导过的IMU的离散 误差状态空间方程,误差状态空间方程两边正好把线性化出来的固定函数值抵消了。之前我们也已经证明了,误差状态空间方程和状态空间方程的系数矩阵是完全相等的,如下所示:
δx^k=Fk−1δxˇk−1+Wk−1wk−1\delta \boldsymbol {\hat{x}}_{k} = \boldsymbol F_{k-1} \delta \boldsymbol {\check{x}}_{k-1} + \boldsymbol W_{k-1} \boldsymbol w_{k-1} δx^k=Fk−1δxˇk−1+Wk−1wk−1
然后是刚才推导过的 误差状态观测方程:
δz=Hkδx^k+Vkvk\delta \boldsymbol z = \boldsymbol H_{k} \delta \boldsymbol {\hat{x}}_{k} + \boldsymbol V_{k} \boldsymbol v_{k} δz=Hkδx^k+Vkvk
把这两个方程带入卡尔曼滤波的五大公式中,我们可以得到以下公式,即为误差状态卡尔曼滤波方程。
预测公式(注意输入项 Buk−1\boldsymbol B \boldsymbol u_{k-1}Buk−1 是我们准确知道的,所以真实状态减名义状态就消去了):
δx^k=Aδxˇk−1P^k=APˇk−1AT+Q\begin{gathered} \delta \boldsymbol {\hat{x}}_{k} = \boldsymbol A \delta \boldsymbol {\check{x}}_{k-1}\\ \boldsymbol {\hat P}_{k} = \boldsymbol A \boldsymbol {\check P}_{k-1} \boldsymbol A^{T}+ \boldsymbol Q \end{gathered} δx^k=Aδxˇk−1P^k=APˇk−1AT+Q
校正公式(注意其中预测观测值 δz\delta \boldsymbol zδz 带入的时候,把噪声 Vkvk\boldsymbol V_{k} \boldsymbol v_{k}Vkvk 简化为0了):
Kk=P^kHTHP^kHT+Rδxˇk=δx^k+Kk(?zm?−δz)=δx^k+Kk(?zm?−Hδx^k)Pˇk=(I−KkH)P^k\begin{gathered} \boldsymbol K_{k}=\frac{ \boldsymbol {\hat P}_{k} \boldsymbol H^{T}}{ \boldsymbol H \boldsymbol {\hat P}_{k} \boldsymbol H^{T} + \boldsymbol R} \\ \delta \boldsymbol {\check {x}}_{k} = \delta \boldsymbol {\hat{x}}_{k} + \boldsymbol {K}_{k}\left( ? \boldsymbol {z}_m? -\delta \boldsymbol z \right) = \delta \boldsymbol {\hat{x}}_{k} + \boldsymbol {K}_{k}\left( ? \boldsymbol {z}_m? \boldsymbol - \boldsymbol H \delta \boldsymbol {\hat{x}}_{k}\right) \\ \boldsymbol {\check P}_{k} =\left( \boldsymbol I- \boldsymbol K_{k} \boldsymbol H\right) \boldsymbol {\hat P}_{k} \end{gathered} Kk=HP^kHT+RP^kHTδxˇk=δx^k+Kk(?zm?−δz)=δx^k+Kk(?zm?−Hδx^k)Pˇk=(I−KkH)P^k
但是带入的时候我们发现了问题,原来的状态卡尔曼滤波我们在校正的时候,KkK_kKk 乘以的系数是 观测传感器测量值 −-− 带入预测状态到观测方程中得到的 预测观测值。这里换成误差状态后,误差的预测观测值我们已经推导出来了,就是 Hδx^k\boldsymbol H \delta \boldsymbol {\hat{x}}_{k}Hδx^k。按理说原本状态卡尔曼滤波中的 传感器测量值zm\boldsymbol {z}_mzm 也应该替换成 传感器测量误差值,那么测量误差值应该怎么计算呢?
其实仔细思考公式(44),即 δz=Hkδx^k+Vkvk\delta \boldsymbol z = \boldsymbol H_{k} \delta \boldsymbol {\hat{x}}_{k} + \boldsymbol V_{k} \boldsymbol v_{k}δz=Hkδx^k+Vkvk,这个公式我们在计算什么?因为方程中 已经把传感器的测量噪声项的影响 Vkvk\boldsymbol V_{k} \boldsymbol v_{k}Vkvk 建模进去了,所以我们计算的是 仅仅由先验状态误差 引起的 观测测量值误差。那么我们上面说的传感器测量值误差应该是什么呢?显然就是 传感器的测量噪声 Vkvk\boldsymbol V_{k} \boldsymbol v_{k}Vkvk!因为传感器测量误差就是在说,如果我传入的 先验状态就是当前的真实状态,但是带入观测方程中计算得到的观测测量值 仍然 和传感器的真实测量值之间有差距,这个差距就是因为我在带入观测方程中计算的时候由于不知道此时传感器的噪声是多少,所以把它简化成了 0,从而计算结果和真实的传感器测量不一致。明白了这个道理之后,就很容易计算 传感器的测量误差值 了,如下所示:
δzm=zm−zxkt=zm−(h(x^k,0)+Hk(xk−x^k))=zm−h(x^k,0)−Hkδx^k\begin{aligned} \delta \boldsymbol z_m &= \boldsymbol z_m - \boldsymbol z_{\boldsymbol x_{kt}} \\ &= \boldsymbol z_m - \left(\boldsymbol h(\boldsymbol {\hat{x}}_{k}, \boldsymbol 0) + \boldsymbol H_{k} (\boldsymbol x_{k} - \boldsymbol {\hat{x}}_{k}) \right) \\ &= \boldsymbol z_m - \boldsymbol h(\boldsymbol {\hat{x}}_{k}, \boldsymbol 0) - \boldsymbol H_{k} \delta \boldsymbol {\hat{x}}_{k} \end{aligned} δzm=zm−zxkt=zm−(h(x^k,0)+Hk(xk−x^k))=zm−h(x^k,0)−Hkδx^k
注意:
(1) 同理还是之前那一点,我们带入真实状态计算观测测量值的时候,带入的仍然是线性化之后的观测方程,即 zk=h(x^k,0)+Hk(xk−x^k)+Vkvk\boldsymbol z_{k} = \boldsymbol h(\boldsymbol {\hat{x}}_{k}, \boldsymbol 0) + \boldsymbol H_{k} (\boldsymbol x_{k} - \boldsymbol {\hat{x}}_{k}) + \boldsymbol V_{k} \boldsymbol v_{k}zk=h(x^k,0)+Hk(xk−x^k)+Vkvk 中计算。
(2) 计算真实状态的测量误差值的时候,我们不知道噪声,所以计算公式中没有 Vkvk\boldsymbol V_{k} \boldsymbol v_{k}Vkvk 这一项。实际上我们上面的公式就是在求噪声,就是在求 Vkvk\boldsymbol V_{k} \boldsymbol v_{k}Vkvk 这一项。
因此,误差卡尔曼滤波中的校正公式为:
δxˇk=δx^k+Kk((zm−h(x^k,0)−Hkδx^k)−Hδx^k)=δx^k+Kk(zm−h(x^k,0)−2Hkδx^k)\begin{aligned} \delta \boldsymbol {\check {x}}_{k} &= \delta \boldsymbol {\hat{x}}_{k} + \boldsymbol {K}_{k}\left( \boldsymbol ( \boldsymbol z_m - \boldsymbol h(\boldsymbol {\hat{x}}_{k}, \boldsymbol 0) - \boldsymbol H_{k} \delta \boldsymbol {\hat{x}}_{k}) - \boldsymbol H \delta \boldsymbol {\hat{x}}_{k}\right) \\ &=\delta \boldsymbol {\hat{x}}_{k} + \boldsymbol {K}_{k}\left( \boldsymbol {z}_m - \boldsymbol h(\boldsymbol {\hat{x}}_{k}, \boldsymbol 0) - 2\boldsymbol H_{k} \delta \boldsymbol {\hat{x}}_{k} \right) \end{aligned} δxˇk=δx^k+Kk((zm−h(x^k,0)−Hkδx^k)−Hδx^k)=δx^k+Kk(zm−h(x^k,0)−2Hkδx^k)
4. 误差状态卡尔曼滤波方程细节问题
1. 状态的更新
每当我们进行一次误差卡尔曼滤波之后,即得到了 后验误差 之后,都需要把它加到 先验的状态值 上,即:
xˇk=x^k+δxˇk\boldsymbol {\check x_k} = \boldsymbol {\hat x_k} + \delta \boldsymbol {\check {x}}_{k} xˇk=x^k+δxˇk
此时我们就得到了经过这次卡尔曼滤波之后,我们得到的 对状态xk\boldsymbol {x}_kxk 的最优估计,所以说此时我们要把后验误差 δxˇk\delta \boldsymbol {\check x_k}δxˇk 置为 0\boldsymbol 00,表示此时我们得到的状态就是我们 能够给出的最优估计的状态结果。
2. 先验估计误差的值和初始化问题
(1)非初始化状态
根据上面状态更新中的操作可以知道,每一次(假设第kkk次)误差状态卡尔曼滤波结束之后,我们的后验误差δxˇk\delta \boldsymbol {\check x_k}δxˇk都是0\boldsymbol 00,表示这次我们给出的状态估计结果是最优的状态估计结果。
那么当下一次(即第k+1k+1k+1次)误差迭代卡尔曼滤波来的时候,我们首先使用IMU状态方程计算这一次(第k+1k+1k+1次)的先验误差δx^k+1\delta \boldsymbol {\hat x}_{k+1}δx^k+1如下,注意公式中没有过程噪声Wkwk\boldsymbol {W}_{k} \boldsymbol {w}_kWkwk项,因为噪声我们始终都是不知道的。
δx^k+1=Aδxˇk\delta \boldsymbol {\hat{x}}_{k+1} = \boldsymbol A \delta \boldsymbol {\check{x}}_{k} δx^k+1=Aδxˇk
这里就会发现由于上一次的后验误差是0,所以这一次我们的先验误差计算结果也是0。所以只要不是在第一次进行误差状态卡尔曼滤波,那么卡尔曼校正公式都可以化简为:
δxˇk=Kk(zm−h(x^k,0))\delta \boldsymbol {\check {x}}_{k} = \boldsymbol {K}_{k}\left ( \boldsymbol z_m - \boldsymbol h(\boldsymbol {\hat{x}}_{k}, \boldsymbol 0)\right) δxˇk=Kk(zm−h(x^k,0))
所以实际上,这个公式才是在误差状态卡尔曼滤波中最常见的校正公式!
(2)初始化状态
那么问题来了,第一次进行误差状态卡尔曼滤波的时候,先验误差x^0\boldsymbol {\hat x_0}x^0如何给定呢?这个问题和卡尔曼滤波问题是一样的,其实卡尔曼滤波问题也存在初始化问题,就是第一次的先验状态给多少?这个感觉就是凭工程经验,靠调参来解决。所以这个也是r2live中存在一段函数进行ESKF初始化的原因。
3. 另一个角度思考卡尔曼滤波和误差卡尔曼滤波的校正公式
经过上面的公式推导,其实我们已经比较清楚为何ESKF和EKF的校正公式为什么看起来相差比较大了,二者校正公式:
EKF:
xˇk=x^k+Kk(zm−Hx^k)\boldsymbol {\check {x}}_{k} = \boldsymbol {\hat{x}}_{k} + \boldsymbol {K}_{k}\left( \boldsymbol {z}_m - \boldsymbol H \boldsymbol {\hat{x}}_{k}\right) xˇk=x^k+Kk(zm−Hx^k)
ESKF:
初始化状态:δxˇk=δx^k+Kk((zm−h(x^k,0)−Hkδx^k)−Hδx^k)一般状态:δxˇk=Kk(zm−h(x^k,0))初始化状态:\delta \boldsymbol {\check {x}}_{k} = \delta \boldsymbol {\hat{x}}_{k} + \boldsymbol {K}_{k}\left( \boldsymbol ( \boldsymbol z_m - \boldsymbol h(\boldsymbol {\hat{x}}_{k}, \boldsymbol 0) - \boldsymbol H_{k} \delta \boldsymbol {\hat{x}}_{k}) - \boldsymbol H \delta \boldsymbol {\hat{x}}_{k}\right) \\ 一般状态: \delta \boldsymbol {\check {x}}_{k} = \boldsymbol {K}_{k}\left ( \boldsymbol z_m - \boldsymbol h(\boldsymbol {\hat{x}}_{k}, \boldsymbol 0)\right) 初始化状态:δxˇk=δx^k+Kk((zm−h(x^k,0)−Hkδx^k)−Hδx^k)一般状态:δxˇk=Kk(zm−h(x^k,0))
但是从数据融合的意义上来想好像又不明白为什么 ESKF 中一般状态下的先验误差为什么是0。其实可以不从数据融合的意义上想,而是从 状态调整的角度 这么想:我们先由状态方程得到一个先验状态,此时我们只有这个先验状态,而且它给出的也是我们 从先验方程中能够得到的最优的状态,所以如果没有观测方程,那么 先验状态的误差就是0,因为这是我们能够给出的最优估计结果。但是现在我们有观测方程,所以我们就想利用观测方程的观测结果,在我们的先验状态的基础上进行一些调整,得到更加准确的后验状态,而调整的大小就是卡尔曼增益所在的这一项。
4. 思考为什么能直接把误差状态方程带入KF中变成ESKF?
从B站DR_CAN推导KF的公式中看,求卡尔曼增益的时候,利用的是对 后验误差的协防差矩阵的迹(就是方差的和)求导为0,即 让后验误差的方差总和达到最小值。那么同理如果现在状态向量变成了误差状态,那推导的时候不就变成对 误差的后验误差的协方差矩阵的迹 求导了吗?这又出来一个 误差的误差?
实际上从应用来说,不需要考虑到推导这一步。因为卡尔曼滤波的方程推导出来五大公式,会根据状态方程和观测方程用就可以了。观察我们上面推导出来了误差的状态方程和误差的观测方程,就简单的认为 误差 是另一个 新的状态变量y\boldsymbol yy 就可以了,然后它就和原来的状态变量没有任何区别,就可以直接带入到卡尔曼滤波的方程中了。

相关文章:

Kalman Filter in SLAM (6) ——Error-state Kalman Filter (EsKF, 误差状态卡尔曼滤波)
文章目录0.前言1. IMU的误差状态空间方程2. 误差状态观测方程3. 误差状态卡尔曼滤波4. 误差状态卡尔曼滤波方程细节问题0.前言 这里先说一句:什么误差状态卡尔曼?完全就是在扯淡! 回想上面我们推导的IMU的误差状态空间方程,其实…...
centos7部署KVM虚拟化
目录 centos7部署KVM虚拟化平台 1、新建一台虚拟机 2、系统内的操作 1、修改主机名 2、挂载镜像光盘 3、ssh优化 4、设置本地yum仓库 5、关闭防火墙,selinux 3、安装KVM 4、设置KVM网络 5、KVM部署与管理 6、使用虚拟系统管理器管理虚拟机 创建存储池 …...

【华为机试真题详解 Python实现】最小施肥机能效【2023 Q1 | 100分】
文章目录 前言题目描述输入描述输出描述示例 1输入:输出:示例 2输入:输出:题目解析参考代码暴力解法二分法前言 《华为机试真题详解》专栏含牛客网华为专栏、华为面经试题、华为OD机试真题。 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可…...
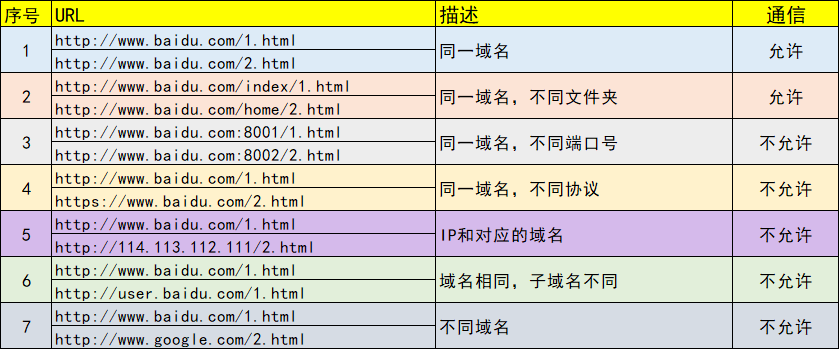
SpringBoot - 什么是跨域?如何解决跨域?
什么是跨域? 在浏览器上当前访问的网站,向另一个网站发送请求,用于获取数据的过程就是跨域请求。 跨域,是浏览器的同源策略决定的,是一个重要的浏览器安全策略,用于限制一个 origin 的文档或者它加载的脚本…...
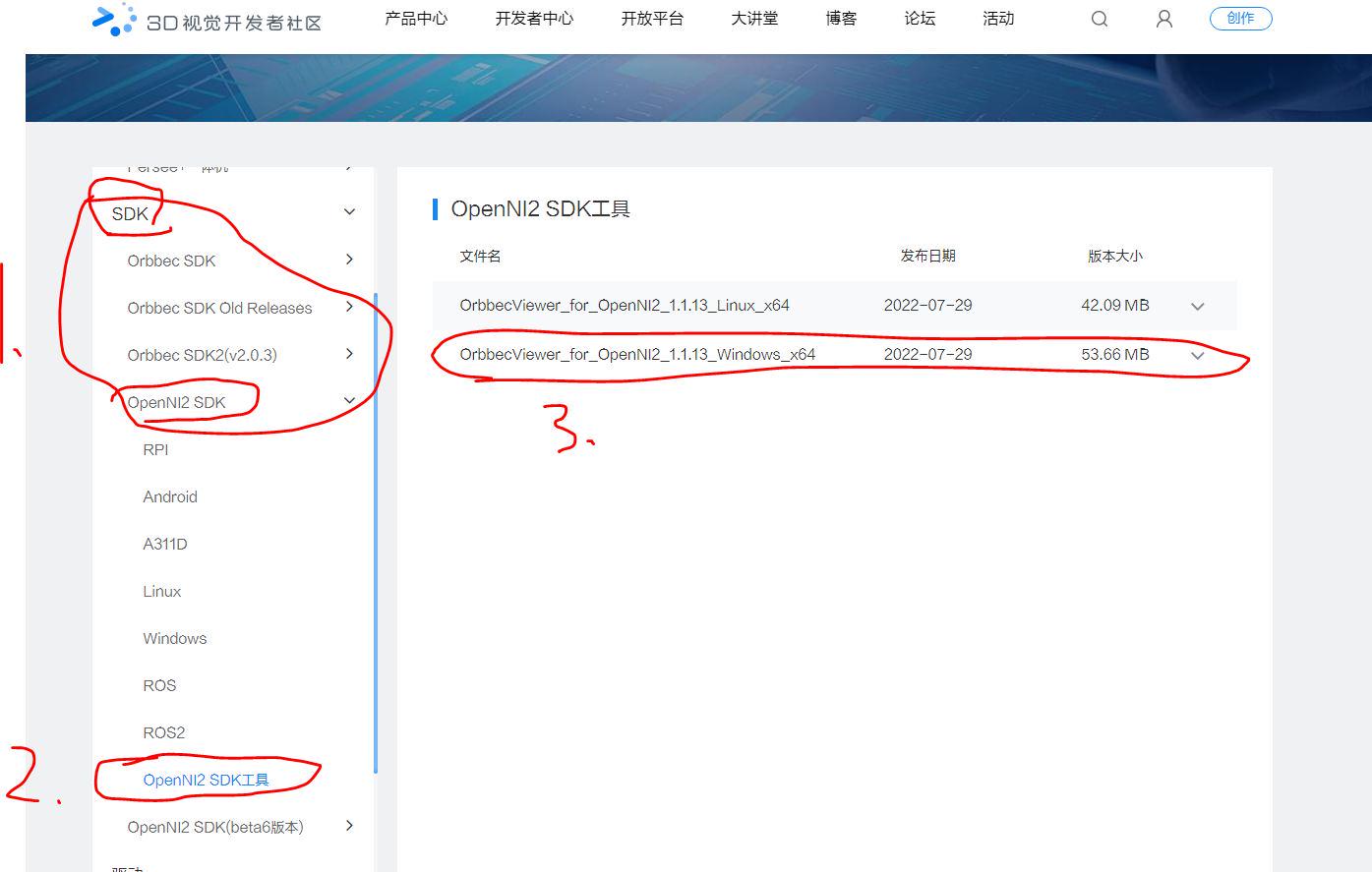
Astra pro相机使用说明
奥比中光的Astra pro这款相机,目前官网已经搜不到相关信息,应该是停产了。但是很多机器人设备上或者淘宝上还能买到。使用起来经常会出现不同的问题。问题1: 这款相机据网友描述,就是乐视相机LeTMC-520,换了外壳&#…...

扬帆优配|数字经济刮起“东风”,龙头晋级7连板
今日两市共40只涨停股,主要集中于数字经济、6G板块,上一个交易日涨停股为29股;除掉18只ST股及3只一字板新股,共19股涨停。另外,4股封板未遂,整体封板率为83%。 6股封单金额超亿元 从收盘涨停板封单量来看&…...

Day911.DTO和DO为什么要互转 -SpringBoot与K8s云原生微服务实践
DTO和DO为什么要互转 Hi,我是阿昌,今天学习记录的是关于DTO和DO为什么要互转的内容。 一、什么是DTO DTO ,数据传输对象,全称 (Data transfer object),用于网络之间传输通讯的对象模型&#x…...

查找、排序、二叉树的算法,统统记录于此。
文章目录一、查找1. 无序表的顺序查找2. 折半查找3. 分块查找4. 二叉排序树BST5. 哈希表查找二、排序1. 不带哨兵的直接插入排序2. 带哨兵的直接插入排序3. 带哨兵、折半查找的直接插入排序4. 希尔排序5. 冒泡排序6. 快速排序7. 选择排序8. 堆排序9. 归并排序二叉树1. 递归先序…...

如何用Python实现在网页中嵌入YouTube的视频?
要在网页中嵌入YouTube视频,可以使用HTML代码,在Python中使用字符串拼接的方式生成HTML代码。下面是一个示例代码,可以生成嵌入YouTube视频的HTML代码: def embed_youtube_video(video_id, width560, height315): """ 生成嵌…...
Easy Deep Learning——PyTorch中的自动微分
目录 什么是深度学习?它的实现原理是怎么样的呢? 什么是梯度下降?梯度下降是怎么计算出最优解的? 什么是导数?求导对于深度学习来说有何意义? PyTorch 自动微分(自动求导) 为什么…...

【生物信息】利用ChatGPT解释GO分析中的关于Biological Processes的问题
利用ChatGPT解释GO分析中的一些问题 如何理解GO中的evidence:ISS,这是什么?qualifier:involved_in是什么意思?evidence:TAS是什么?evidence: IBA是什么?evidence: IMP是什么?evidence:IDA是什么?evidence: IEA是什么?GO分析中,evidence: NAS是什么意思?GO分析中…...

2018年MathorCup数学建模C题陆基导弹打击航母的数学建模与算法设计解题全过程文档及程序
2018年第八届MathorCup高校数学建模挑战赛 C题 陆基导弹打击航母的数学建模与算法设计 原题再现: 火箭军是保卫海疆主权的战略力量,导弹是国之利器。保家卫国,匹夫有责。为此,请参赛者认真阅读"陆基反舰导弹打击航母的建模示意图"。(附图 1 )参考图中的…...
打怪升级之CFile类
CFile类 信息源自官方文档:https://learn.microsoft.com/zh-cn/cpp/mfc/reference/cfile-class?viewmsvc-170。 CFile是Microsoft 基础类文件类的基类。它直接提供非缓冲的二进制磁盘输入/输出设备,并直接地通过派生类支持文本文件和内存文件。CFile与…...

[css]通过网站实例学习以最简单的方式构造三元素布局
文章目录二元素布局纵向布局横向布局三元素布局b站直播布局实例左右-下 布局左-上下 布局上下-右 布局方案一方案二后言二元素布局 在学习三元素布局之前,让我们先简单了解一下只有两个元素的布局吧 两个元素的相对关系非常简单,不是上下就是左右 纵向布…...
【冲刺蓝桥杯的最后30天】day6
大家好😃,我是想要慢慢变得优秀的向阳🌞同学👨💻,断更了整整一年,又开始恢复CSDN更新,从今天开始更新备战蓝桥30天系列,一共30天,如果对你有帮助或者正在备…...
ssm框架之spring:浅聊IOC
IOC 前面体验了spring,不过其运用了IOC,至于IOC( Inverse Of Controll—控制反转 ) 看一下百度百科解释: 控制反转(Inversion of Control,缩写为IoC),是面向对象编程中的一种设计原则&#x…...
pytest初识
一、单元测试框架 (1)什么是单元测试框架? 单元测试是指在软件开发中,针对软件的最小单元(函数、方法)进行正确性的检查测试 (2)单元测试框架 java:junit和testng pytho…...
-12)
设计模式~责任链模式(Chain of Responsibility)-12
目录 (1)优点 (2)缺点 (3)使用场景 (4)注意事项: (5)应用实例: (6)经典案例 代码 责任链, …...

【ElasticSearch】(一)—— 初识ES
文章目录1. 了解ES1.1 elasticsearch的作用1.2 ELK技术栈1.3 elasticsearch和lucene1.4 为什么不是其他搜索技术?1.5 总结2. 倒排索引2.1 正向索引2.2 倒排索引2.3 正向和倒排3. ES的一些概念3.1 文档和字段3.2 索引和映射3.3 mysql与elasticsearch1. 了解ES Elasti…...
MySQL 事务隔离
MySQL 事务隔离事务隔离实现事务的启动ACID : 原子(Atomicity)、一致(Consistency)、隔离(Isolation)、永久(Durability) 多个事务可能出现问题 : 脏读 (dirty read) , 不可重复读 (non-repeatable read) , 幻读 (phantom read) 事务隔离级别 : 读未提交 (read uncommitted)…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
