day34 贪心算法 455.分发饼干 376. 摆动序列
贪心算法理论基础
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
贪心一般解题步骤(贪心无套路):
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
455.分发饼干
这里的局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩
或者是
局部最优就是小饼干喂给胃口小的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩
注意事项:注意两种情况
//大饼干满足胃口大的孩子 (最大饼干一定要用所以for控制胃口)
代码中先遍历的胃口,在遍历的饼干,那么可不可以 先遍历 饼干,在遍历胃口呢?其实是不可以的。外面的 for 是里的下标 i 是固定移动的,而 if 里面的下标 index 是符合条件才移动的。
如果 for 控制的是饼干, if 控制胃口,就是出现如下情况 :、

if 里的 index 指向 胃口 10, for 里的 i 指向饼干 9,因为 饼干 9 满足不了 胃口 10,所以 i 持续向前移动,而 index 走不到s[index] >= g[i] 的逻辑,所以 index 不会移动,那么当 i 持续向前移动,最后所有的饼干都匹配不上。 所以 一定要 for 控制 胃口,里面的 if 控制饼干。
//小饼干满足胃口小的孩子 for控制饼干 if控制胃口(最小胃口一定要被喂所以for控制饼干)
//大饼干满足胃口大的孩子
class Solution {public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int index = s.length - 1;int result = 0 ;for (int i = g.length -1; i >=0; i--) {if(index >=0 && s[index] >= g[i]){index--;result++;}}return result;}
}//小饼干满足胃口小的孩子
class Solution {public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int index = 0;for (int i = 0; i < s.length; i++) {if(index < g.length && g[index] <= s[i]){index++;}}return index;}
}误区
如果说使用这种代码的话,使用while判断可能会导致重复技术即g[1,2,3] s[1,1]会导致结果为2而不是正确的情况只满足一个孩子,所以判断使用if。
for (int i = g.length -1; i >=0; i--) {while(index >=0 && s[index] >= g[i]){index--;result++;}
}376. 摆动序列

局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列
实际操作上,其实连删除的操作都不用做,因为题目要求的是最长摆动子序列的长度,所以只需要统计数组的峰值数量就可以了(相当于是删除单一坡度上的节点,然后统计长度),这就是贪心所贪的地方,尽可能的保持峰值,然后删除单一坡度上的节点
大体思路:
在计算是否有峰值的时候,遍历下标 i ,计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i]),如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 此时就有波动就需要统计。
三种情况:
- 情况一:上下坡中有平坡
- 情况二:数组首尾两端
- 情况三:单调坡中有平坡
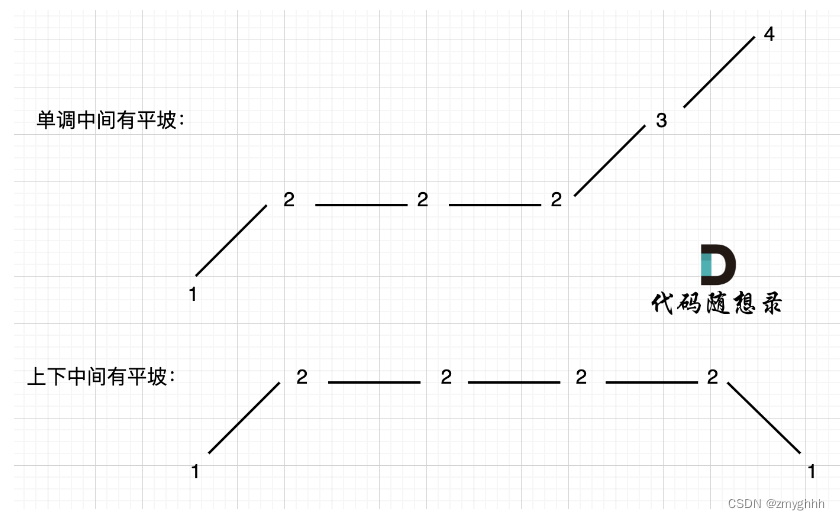
上下坡中有平坡

在图中,当 i 指向第一个 2 的时候,prediff > 0 && curdiff = 0 ,当 i 指向最后一个 2 的时候 prediff = 0 && curdiff < 0。
如果我们采用,删左面三个 2 的规则,那么 当 prediff = 0 && curdiff < 0 也要记录一个峰值,因为他是把之前相同的元素都删掉留下的峰值。
所以我们记录峰值的条件应该是: (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0),为什么这里允许 prediff == 0 ,就是为了 上面我说的这种情况。
情况二:数组首尾两端(prediff=0为了解决数组最左端 最右端初始化为0)
如果只有两个不同的元素,那摆动序列也是 2。
可以假设,数组最前面还有一个数字,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即 preDiff = 0,如图:

针对以上情形,result 初始为 1(默认最右面有一个峰值)
情况三:单调坡度有平坡(解决情况2出现的问题在坡度有变化时再prediff = curdiff)
我们忽略了一种情况,即 如果在一个单调坡度上有平坡,例如[1,2,2,2,3,4],如图:

在三个地方记录峰值,但其实结果因为是 2,因为 单调中的平坡 不能算峰值(即摆动)。
那么我们应该什么时候更新 prediff 呢?
我们只需要在 这个坡度 摆动变化的时候,更新 prediff 就行,这样 prediff 在 单调区间有平坡的时候 就不会发生变化,造成我们的误判。
总结:
本题异常情况的本质,就是要考虑平坡, 平坡分两种,一个是 上下中间有平坡,一个是单调有平坡,如图:
class Solution {public int wiggleMaxLength(int[] nums) {if(nums.length <=1)return nums.length;int prediff = 0;int curdiff =0;int count = 1;for (int i = 1; i < nums.length; i++) {curdiff = nums[i] - nums[i-1];if ((curdiff > 0 && prediff <= 0) || (curdiff < 0 && prediff >= 0)) {count++;prediff = curdiff; //在坡度变化时改变prediff}//prediff = curdiff; 这种写法解决不了单调有平坡的问题}//System.out.println(count);return count;}
}53. 最大子序和
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”
常见误区
误区一:
不少同学认为 如果输入用例都是-1,或者 都是负数,这个贪心算法跑出来的结果是 0, 这是又一次证明脑洞模拟不靠谱的经典案例,建议大家把代码运行一下试一试,就知道了,也会理解 为什么 result 要初始化为最小负数了。
误区二:
大家在使用贪心算法求解本题,经常陷入的误区,就是分不清,是遇到 负数就选择起始位置,还是连续和为负选择起始位置。
在动画演示用,大家可以发现, 4,遇到 -1 的时候,我们依然累加了,为什么呢?
因为和为 3,只要连续和还是正数就会 对后面的元素 起到增大总和的作用。 所以只要连续和为正数我们就保留。
这里也会有录友疑惑,那 4 + -1 之后 不就变小了吗? 会不会错过 4 成为最大连续和的可能性?
其实并不会,因为还有一个变量 result 一直在更新 最大的连续和,只要有更大的连续和出现,result 就更新了,那么 result 已经把 4 更新了,后面 连续和变成 3,也不会对最后结果有影响
class Solution {public int maxSubArray(int[] nums) {if(nums.length == 1)return nums[0];int sum = Integer.MIN_VALUE; //存储最大值int count = 0; //统计大小for (int i = 0; i < nums.length; i++) {count += nums[i];sum = Math.max(sum,count);if(count <= 0) {count = 0;}}return sum;}
}相关文章:

day34 贪心算法 455.分发饼干 376. 摆动序列
贪心算法理论基础 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。 贪心一般解题步骤(贪心无套路): 将问题分解为若干个子问题找出适合的贪心策略求解每一个子问题的最优解将局部最优解堆叠成全局最优解 455.分发饼干 …...
养老院管理系统基于springboot的养老院管理系统java项目
文章目录 养老院管理系统一、项目演示二、项目介绍三、系统部分功能截图四、部分代码展示五、底部获取项目源码(9.9¥带走) 养老院管理系统 一、项目演示 养老院管理系统 二、项目介绍 基于springboot的养老院管理系统 角色:超级…...

跳台阶扩展问题
题目链接 f(1) 1f(2) 1 1 2f(3) 1 2 1 4f(4) 1 2 4 1 8 所以 f(n) 2 n − 1 ^{n-1} n−1 import java.util.Scanner;public class Solution {public int jumpFloorII(int target) {return 1 << (target - 1);} }...

超清高帧,成像升级 | SWIR短波红外相机500万像素992芯片
博图光电5MP短波红外相机,搭载了索尼IMX992 SenSWIR传感器,支持5.2MP分辨率,适合探测波长在400nm-1700nm波段的可见光和短波红外光,有效面积和透光率得到提升,内置TEC制冷片,实现了像素尺寸和图像均匀性方面…...

攻击渗透思考题
1. windows登录的明文密码,存储过程是怎么样的,密文存在哪个文件下,该文件是否可以打开,并且查看到密文 在Windows操作系统中,登录时输入的明文密码不会以明文形式存储在系统中。相反,Windows使用一种称为“…...

Flutter 中的 Opacity 小部件:全面指南
Flutter 中的 Opacity 小部件:全面指南 在Flutter中,动画和视觉效果是提升用户体验的重要手段。Opacity小部件允许你改变子组件的透明度,从而实现淡入、淡出或其它透明度相关的动画效果。本文将提供Opacity的全面指南,帮助你了解…...

【介绍下如何在SQL中添加数据】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...
【Linux学习】深入了解Linux中进程状态及其转换
文章目录 进程状态进程排队进程的状态(运行,阻塞,挂起)进程的七个状态 孤儿进程 进程状态 进程 task_struct 可执行程序 进程不是一 直在运行的,可能在等待软硬件资源,比如scanf后,程序停止运…...

【Python设计模式11】建造者模式
建造者模式(Builder Pattern)是一种创建型设计模式,它将一个复杂对象的构建过程分离出来,使得同样的构建过程可以创建不同的表示。建造者模式通过使用多个简单的对象一步一步构建成一个复杂的对象。 建造者模式的结构 建造者模式…...

coredump文件生成配置
1.打开coredump文件生成开关 查看开关是否打开:ulimit -a 如果core file size 为0,则为关闭。 执行:ulimit -c 10240 将其coredump文件大小设置。 2.coredump文件保存位置: /proc/sys/kernel/core_pattern文件可以控制core文…...

jmeter线程组(下篇)
线程组 线程组作为JMeter测试计划的核心组件之一,对于模拟并发用户的行为至关重要。线程组元件是整个测试计划的入口,所有的取样器和控制器必须放置在线程组下。 可以将线程组视为一个虚拟用户池,其中每个线程可被理解为一个虚拟用户&#x…...

Stable Diffusion【写实模型】:逼真,逼真,超级逼真的国产超写实摄影大模型万享XL
今天和大家分享的是一个国产万享系列中使用量最高的大模型:万享XL_超写实摄影,顾名思义,该大模型主要是面向写实摄影,一方面生成的图片人物皮肤纹理细节超级逼真,另一方面对于光影效果的处理也非常到位。对于万享XL超写实摄影大模…...

Android 13 配置默认DN
需求: 如果存在用户配置的DNS服务器,则切面拦截运行商下发的DNS,替换为用户自己配置的DNS. 实现: 直接上代码: 1:TelephonyProperties 内新增属性保存用户设置的dns //QSSI.13/frameworks/base/telephony/java/com/android/in…...
系统开发与运行知识
系统开发与运行知识 导航 文章目录 系统开发与运行知识导航一、软件工程二、软件生命周期三、开发模型四、开发方法五、需求分析结构化分析 六、数据流图分层数据流图的画法设计注意事项 七、数据字典数据字典的内容 八、系统设计九、结构化设计常用工具十、面向对象十一、UML…...

算法训练 | 二叉树Part1 | 递归遍历、迭代遍历、统一迭代
目录 递归遍历 前序遍历 迭代遍历 前序遍历(迭代法) 中序遍历(迭代法) 后序遍历(迭代法) 统一迭代法 统一迭代 嵌入式学习分享个人主页:Orion嵌入式随想录 - 小红书 (xiaohongshu.com) …...
AcWing 2568:树链剖分 ← 线段树+DFS
【题目来源】https://www.acwing.com/problem/content/2570/【题目描述】 给定一棵树,树中包含 n 个节点(编号 1∼n),其中第 i 个节点的权值为 ai。 初始时,1 号节点为树的根节点。 现在要对该树进行 m 次操作…...
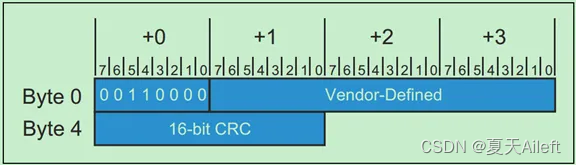
PCIe协议之-DLLP详解
✨前言: 🌟数据链路层的功能 数据链路层将从物理层中获得报文, 并将其传递给事务层; 同时接收事务层的报文, 并将其转发到物理层; 核心的功能有以下三点 1.保证TLP在 PCIe 链路中的正确传递; 2.数据链路层使用了容错…...
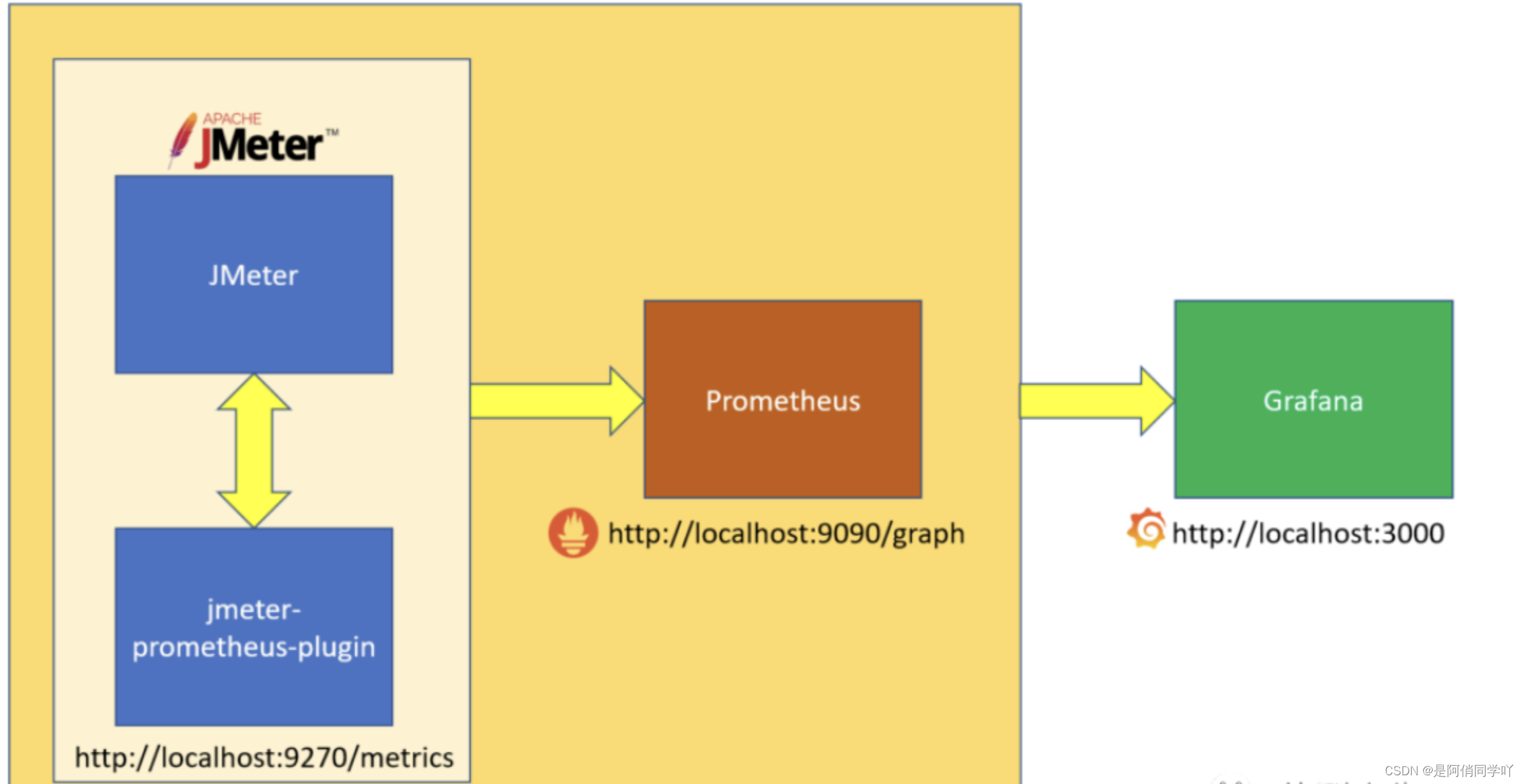
Jmeter+prometheus+grafana性能测试
文章目录 Jmeterprometheusgrafana性能测试背景目标设计思路原理案例启发 Jmeterprometheusgrafana性能测试 背景 在现代社会中,人们对于应用程序的响应速度和性能体验提出了越来越高的要求。无论是电子商务网站、社交媒体平台还是企业级软件系统,都…...
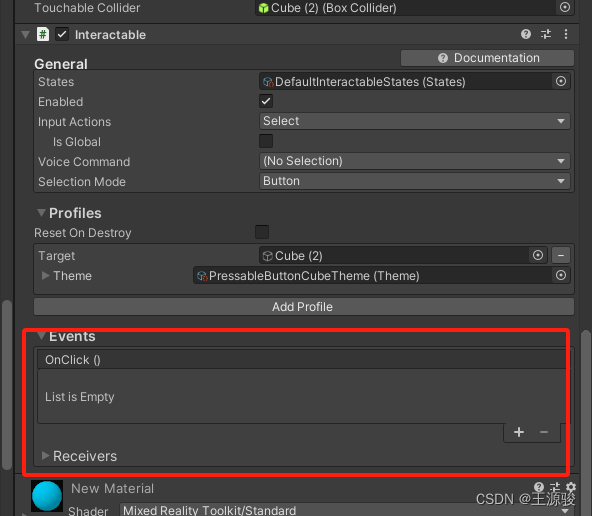
Hololens 2 新建自定义按钮
官方链接地址 1、创建Cube 2、添加PressableButton脚本,并点击AddNearin… 3、把Cube拖入到MovingButtonVisuals变量中 4、点击NearInteractionTouchable组件(这个组件是添加和上一个脚本绑定的,自动添加上来的)上的Fix… 5、…...

景源畅信:抖音小店新手小白如何做好运营?
在数字时代的浪潮中,抖音小店成为了众多创业者和商家的新宠。但面对激烈的市场竞争和不断变化的平台规则,新手小白如何才能在抖音小店的海洋里稳健航行,捕捉到属于自己的商机呢?接下来的内容将为你揭晓答案。 一、精准定位,明确目…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
