北大国际医院腹膜后纤维化课题组 多学科协作开辟治疗新径
腹膜后纤维化(Retroperitoneal Fibrosis,简称RPF)是一种罕见的自身免疫性疾病,其核心特征是纤维组织的异常增生与硬化。这种疾病主要影响肾脏下方的腹主动脉和髂动脉区域,增生的纤维组织会逐渐压迫周围的输尿管和下腔静脉,从而导致一系列并发症,包括主动脉瘤、肾功能衰竭等,甚至可能危及生命。糖皮质激素是治疗RPF的主要手段,但疗效有限且伴随显著副作用。
而腹膜后纤维化(RPF)的规范诊治涉及包括风湿免疫学、腹膜后肿瘤学、泌尿外科学、肾内科学和血管外科学等多个学科。因此,北京大学国际医院自2017年起成立了专门的腹膜后纤维化课题组,并开设了专病联合门诊,致力于探索更有效的治疗方案,更好的为患者服务。北京大学国际医院RPF专病联合门诊近年来收治腹膜后纤维化患者总数和年收治人数均位于全国前列,对于该病的系统性诊治及研究已成为北京大学国际医院风湿免疫科和腹膜后肿瘤外科联合特色,现有多项临床研究正在进行中。经过多年的努力,课题组现已成为全国在RPF诊治和研究方面的领军团队之一。
研究团队对腹膜后纤维化的疾病-基因-药物数据库进行检索分析,锁定与病理有关的关键蛋白,并进行药物匹配度计算,据此设计出临床用药实验——采用针对炎症和关键病理机制进行双重抑制的“鸡尾酒疗法”(即激素联合西罗莫司治疗),并在腹膜后纤维化病人中进行系统观察和评估。研究结果发现,此疗法有效控制长期使用激素的副作用,有望取代该病的传统糖皮质激素单药治疗方案。该研究提供了一种生物信息学辅助实验室探索走向临床应用的转化研究策略,为临床试验提供了精准的干预靶点,目前该临床研究仍在持续招募患者中。
随着新疗法的研究持续推进,我们期待未来能够为更多RPF患者带来福音。北京大学国际医院的专家团队将继续致力于这一疾病的研究,不断探索和优化治疗方案,以期达到更好的治疗效果,改善患者的生活质量。
相关文章:

北大国际医院腹膜后纤维化课题组 多学科协作开辟治疗新径
腹膜后纤维化(Retroperitoneal Fibrosis,简称RPF)是一种罕见的自身免疫性疾病,其核心特征是纤维组织的异常增生与硬化。这种疾病主要影响肾脏下方的腹主动脉和髂动脉区域,增生的纤维组织会逐渐压迫周围的输尿管和下腔静脉,从而导致一系列并发症,包括主动脉瘤、肾功能衰竭等,甚至…...

面试数据库八股文十问十答第七期
面试数据库八股文十问十答第七期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的!关注专栏后就能收到持续更新! ⭐点赞⭐收藏⭐不迷路!⭐ 1)索引是越多越好吗ÿ…...
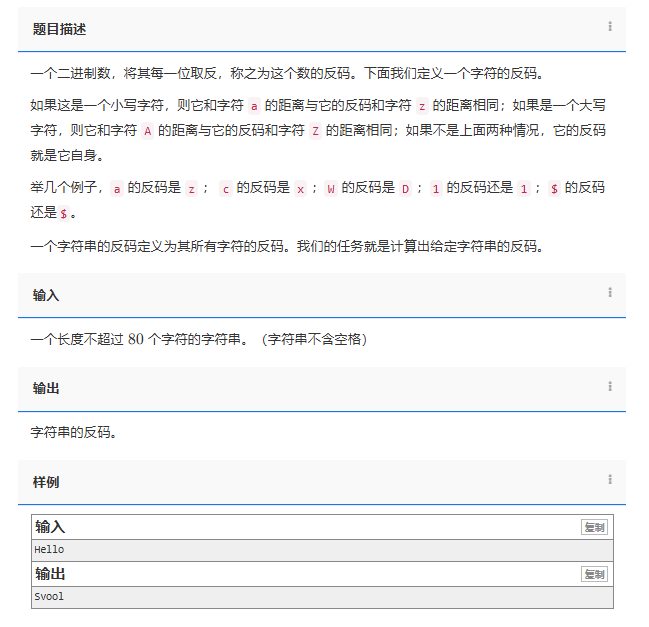
【C++题解】1133. 字符串的反码
问题:1133. 字符串的反码 类型:字符串 题目描述: 一个二进制数,将其每一位取反,称之为这个数的反码。下面我们定义一个字符的反码。 如果这是一个小写字符,则它和字符 a 的距离与它的反码和字符 z 的距离…...
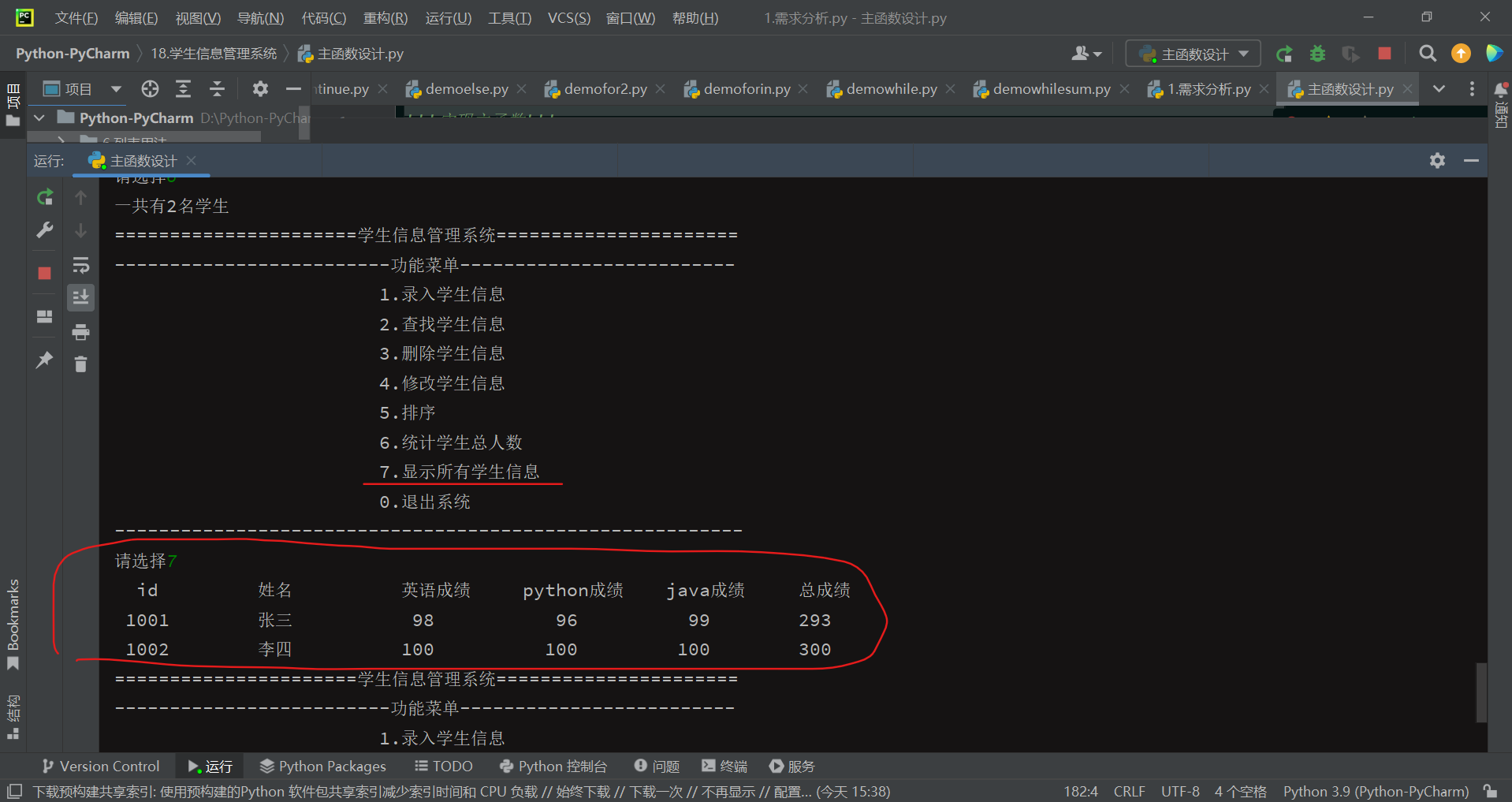
【Python编程实战】基于Python语言实现学生信息管理系统
🎩 欢迎来到技术探索的奇幻世界👨💻 📜 个人主页:一伦明悦-CSDN博客 ✍🏻 作者简介: C软件开发、Python机器学习爱好者 🗣️ 互动与支持:💬评论 &…...

AI网络爬虫:批量爬取电视猫上面的《庆余年》分集剧情
电视猫上面有《庆余年》分集剧情,如何批量爬取下来呢? 先找到每集的链接地址,都在这个class"epipage clear"的div标签里面的li标签下面的a标签里面: <a href"/drama/Yy0wHDA/episode">1</a> 这个…...

md5强弱碰撞
一,类型。 1.弱比较 php中的""和""在进行比较时,数字和字符串比较或者涉及到数字内容的字符串,则字符串会被转换为数值并且比较按照数值来进行。按照此理,我们可以上传md5编码后是0e的字符串,在…...

【Docker故障处理篇】运行容器报错“docker: failed to register layer...file exists.”解决方法
【Docker故障处理篇】运行容器报错“docker: failed to register layer...file exists.” 一、Docker环境介绍2.1 本次环境介绍2.2 本次实践介绍二、故障现象2.1 运行容器消失2.2 重新运行容器报错三、故障分析四、故障处理4.1 停止 Docker 服务:4.2 备份重要数据4.3 清理冲突…...
 一面面经)
小红书-社区搜索部 (NLP、CV算法实习生) 一面面经
😄 整个流程按如下问题展开,用时60min左右面试官人挺好,前半部分问问题,后半部分coding一道题。 各位有什么问题可以直接评论区留言,24小时内必回信息,放心~ 文章目录 1、自我介绍2、介绍下项目:微信-多模态小视频分类2.1、看你用了cross-att来融合多模态信息,cross…...
解读makefile中的.PHONY
在 Makefile 中,.PHONY 是一个特殊的目标,用于声明伪目标(phony target)。伪目标是指并不代表实际构建结果的目标,而是用来触发特定动作或命令的标识。通常情况下,.PHONY 会被用来声明一组需要执行的动作&a…...

linux配置防火墙端口
配置防火墙,添加或删除端口,需要有root权限。 防火墙常用命令如下: 1.查看防火墙状态: systemctl status firewalld active(running):开启状态,正在运行中 inactive(dead):关闭状态ÿ…...

sklearn线性回归--岭回归
sklearn线性回归--岭回归 岭回归也是一种用于回归的线性模型,因此它的预测公式与普通最小二乘法相同。但在岭回归中,对系数(w)的选择不仅要在训练数据上得到好的预测结果,而且还要拟合附加约束,使系数尽量小…...
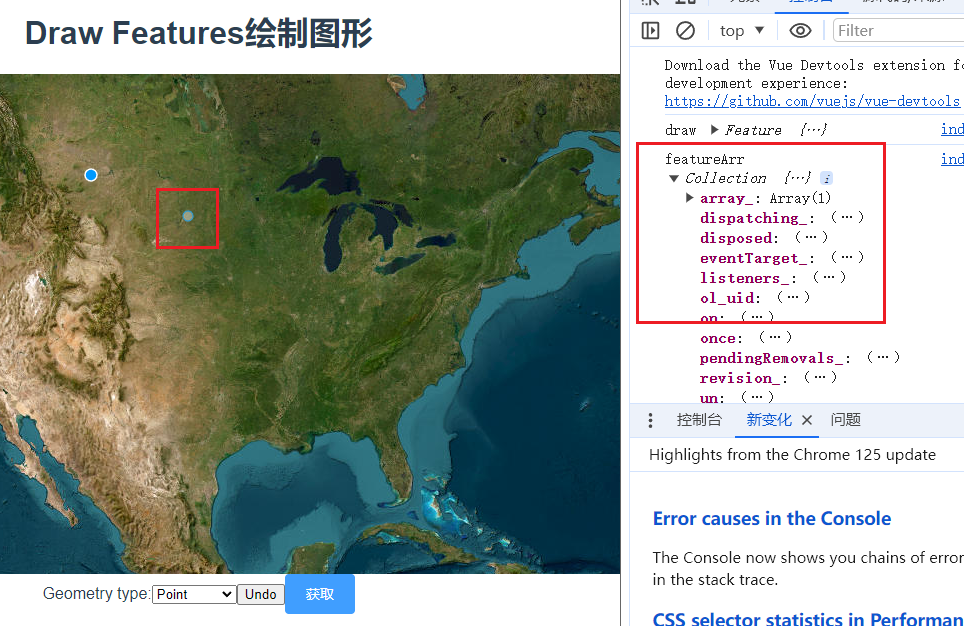
三十一、openlayers官网示例Draw Features解析——在地图上自定义绘制点、线、多边形、圆形并获取图形数据
官网demo地址: Draw Features 先初始化地图,准备一个空的矢量图层,用于显示绘制的图形。 initLayers() {const raster new TileLayer({source: new XYZ({url: "https://server.arcgisonline.com/ArcGIS/rest/services/World_Imagery/…...

医疗科技:UWB模块为智能医疗设备带来的变革
随着医疗科技的不断发展和人们健康意识的提高,智能医疗设备的应用越来越广泛。超宽带(UWB)技术作为一种新兴的定位技术,正在引领着智能医疗设备的变革。UWB模块作为UWB技术的核心组成部分,在智能医疗设备中发挥着越来越…...
)
Java面试题大全(从基础到框架,中间件,持续更新~~~)
从Java基础到数据库,Spring,MyBatis,消息中间件,微服务解决全部Java面试过程中的问题。(持续更新~~) Java基础 2024最新Java面试题——java基础 MySQL基础 mysql基础知识——适合不太熟悉数据库知识的小…...

零知识证明在隐私保护和身份验证中的应用
PrimiHub一款由密码学专家团队打造的开源隐私计算平台,专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。 隐私保护和身份验证是现代社会中的关键问题,尤其是在数字化时代。零知识证明(Zero-Knowledge Proofs&…...

15.微信小程序之async-validator 基本使用
async-validator是一个基于 JavaScript 的表单验证库,支持异步验证规则和自定义验证规则 主流的 UI 组件库 Ant-design 和 Element中的表单验证都是基于 async-validator 使用 async-validator 可以方便地构建表单验证逻辑,使得错误提示信息更加友好和…...

元宇宙vr科普馆场景制作引领行业潮流
在这个数字化高速发展的时代,北京3D元宇宙场景在线制作以其独特的优势,成为了行业内的创新引领者。它能够快速完成空间设计,根据您的个性化需求,轻松设置布局、灯光、音效以及互动元素等,为您打造出一个更加真实、丰富…...

kotlin基础之高阶函数
Kotlin中的高阶函数、内联函数以及noinline和crossinline关键字是函数式编程中的重要概念。下面我将逐一解释这些概念的定义、实现原理、使用场景以及noinline和crossinline关键字的具体用法。 高阶函数 定义:高阶函数是接受一个或多个函数作为参数,或…...

【Python音视频技术】用moviepy实现图文成片功能
今天上班的时候看到有人群里问 图文成片怎么实现。 临时给我提供一点写作的灵感,趁着下班写一篇。这里用到 python的moviepy库, 之前文章介绍过。 大体思路:假定有4张图片,每张图片将在视频中展示2秒钟,并且图片会按照…...

【Linux】权限的理解之权限掩码(umask)
目录 前言 一、利用八进制数值表示文件或目录的权限属性 二、系统默认的权限掩码和权限掩码的作用原理 三、分析权限掩码改变文件或目录的权限属性 前言 权限掩码是由4个数字组合而成的,默认的第一位数字是0;后三位数字分别由八进制位数字组成。权限…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
