拉格朗日插值及牛顿差商方法的实现(Matlab)
一、问题描述
拉格朗日插值及牛顿差商方法的实现。
二、实验目的
掌握拉格朗日插值和牛顿差商方法的原理,能够编写代码实现两种方法;能够分析多项式插值中的误差。
三、实验内容及要求
-
利用拉格朗日插值及牛顿差商方法估计1980 年的人口,并与1980 年的真实值
4452584592 进行比较,观察两种方法的结果是否相同。其中:
(a)利用1970 年和1990 年的数据,得到插值直线,估计1980 年的人口;
(b)利用1960 年、1970、1990 年的数据,得到插值抛物线,估计1980 年的人口;
(c)利用全部数据,估计1980 年的人口。
年份 人口
1960 3039585530
1970 3707475887
1990 5281653820
2000 6079603571 -
现有5 个插值节点:(0.6,1.433329), (0.7, 1.632316), (0.8, 1.896481), (0.9,2.247908), (1.0,2.718282)。
(a)使用牛顿差商方法计算 x = 0.82 和 x = 0.98 的近似值;
(b)上述数据来自函数f(x) = e(x2),使用插值误差公式找出x = 0.82 和x = 0.98 时的误差上界,比较误差界和实际误差。
(c)画出在区间[0.5, 1]上实际的插值误差曲线。
四、算法原理
1. 插值多项式的具体形式
拉格朗日插值多项式:
给定 n + 1 n+1 n+1个插值节点 ( x 0 , y 0 ) , ( x 1 , y 1 ) , . . . , ( x n , y n ) (x_0, y_0), (x_1, y_1), ..., (x_n, y_n) (x0,y0),(x1,y1),...,(xn,yn),拉格朗日插值多项式 L ( x ) L(x) L(x) 的表达式为:
L ( x ) = ∑ i = 0 n y i ⋅ ∏ j = 0 , j ≠ i n x − x j x i − x j L(x) = \sum_{i=0}^{n} y_i \cdot \prod_{j=0, j\neq i}^{n} \frac{x - x_j}{x_i - x_j} L(x)=∑i=0nyi⋅∏j=0,j=inxi−xjx−xj
其中, L ( x ) L(x) L(x) 是 n n n 次多项式,通过 n + 1 n+1 n+1 个插值节点, x x x 是待插值的点。
牛顿差商插值多项式:
给定 n + 1 n+1 n+1个插值节点 ( x 0 , y 0 ) , ( x 1 , y 1 ) , . . . , ( x n , y n ) (x_0, y_0), (x_1, y_1), ..., (x_n, y_n) (x0,y0),(x1,y1),...,(xn,yn),牛顿差商插值多项式 N ( x ) N(x) N(x) 的表达式为:
N ( x ) = y 0 + ( x − x 0 ) ⋅ f [ x 0 , x 1 ] + ( x − x 0 ) ⋅ ( x − x 1 ) ⋅ f [ x 0 , x 1 , x 2 ] + … + ( x − x 0 ) ⋅ ( x − x 1 ) ⋅ … ⋅ ( x − x n − 1 ) ⋅ f [ x 0 , x 1 , . . . , x n ] N(x) = y_0 + (x - x_0) \cdot f[x_0, x_1] + (x - x_0) \cdot (x - x_1) \cdot f[x_0, x_1, x_2] + \ldots + (x - x_0) \cdot (x - x_1) \cdot \ldots \cdot (x - x_{n-1}) \cdot f[x_0, x_1, ..., x_n] N(x)=y0+(x−x0)⋅f[x0,x1]+(x−x0)⋅(x−x1)⋅f[x0,x1,x2]+…+(x−x0)⋅(x−x1)⋅…⋅(x−xn−1)⋅f[x0,x1,...,xn]
其中,差商 f [ x i , x i + 1 , . . . , x j ] f[x_i, x_{i+1}, ..., x_{j}] f[xi,xi+1,...,xj] 的计算方式为:
f [ x i , x i + 1 , . . . , x j ] = f [ x i + 1 , x i + 2 , . . . , x j ] − f [ x i , x i + 1 , . . . , x j − 1 ] x j − x i f[x_i, x_{i+1}, ..., x_{j}] = \frac{f[x_{i+1}, x_{i+2}, ..., x_{j}] - f[x_i, x_{i+1}, ..., x_{j-1}]}{x_j - x_i} f[xi,xi+1,...,xj]=xj−xif[xi+1,xi+2,...,xj]−f[xi,xi+1,...,xj−1]
2. 多项式插值主定理
多项式插值主定理是插值理论的核心定理之一,它表述了一个多项式插值问题的存在唯一性。主定理陈述如下:
如果给定 n + 1 n+1 n+1 个节点 ( x 0 , y 0 ) , ( x 1 , y 1 ) , . . . , ( x n , y n ) (x_0, y_0), (x_1, y_1), ..., (x_n, y_n) (x0,y0),(x1,y1),...,(xn,yn),其中所有的 x i x_i xi 都是互不相同的,则存在唯一一个次数不超过 n n n 的多项式 P ( x ) P(x) P(x) 满足 P ( x i ) = y i P(x_i) = y_i P(xi)=yi,对所有的 i i i 成立。
3. 多项式插值中的误差公式和用途
误差公式:
多项式插值中的误差公式用于估计插值多项式与真实函数之间的误差。对于拉格朗日插值,误差公式为:
∣ f ( x ) − L ( x ) ∣ ≤ M ( n + 1 ) ! ⋅ ∏ i = 0 n ∣ x − x i ∣ |f(x) - L(x)| \leq \frac{M}{(n+1)!} \cdot \prod_{i=0}^{n} |x - x_i| ∣f(x)−L(x)∣≤(n+1)!M⋅∏i=0n∣x−xi∣
其中, M M M 是插值区间内的最大二阶导数的上界。
对于牛顿差商插值,误差公式为:
∣ f ( x ) − N ( x ) ∣ ≤ M 4 ( n + 1 ) ⋅ ∏ i = 0 n ∣ x − x i ∣ |f(x) - N(x)| \leq \frac{M}{4(n+1)} \cdot \prod_{i=0}^{n} |x - x_i| ∣f(x)−N(x)∣≤4(n+1)M⋅∏i=0n∣x−xi∣
其中, M M M 是插值区间内的最大四阶导数的上界。
用途:
- 误差估计: 误差公式用于估计插值多项式的精度,帮助确定插值点的选择和插值多项式的次数。
- 数据逼近: 插值多项式可以用于逼近实际数据,使得在已知数据点上的拟合更为精确。
- 数值计算: 插值多项式在数值计算中广泛应用,例如在数值积分和数值微分等问题中。
综上所述,插值方法通过构造插值多项式在给定节点上与已知数据一致,提供了一种在非常有限数据点上估计未知函数值的方法,并通过误差估计帮助控制插值的精度。
五、测试数据及结果
- 针对(a)(b)(c)三种情况,分别给出拉格朗日插值及牛顿差商方法的估计值(保留4 位小数)。给出3 种情况下的误差(保留4 位小数),分析是否插值多项式次数越高,近似结果越好。
- 代码:
% 拉格朗日插值函数
function result = lagrange_interpolation(x, y, xi)n = length(x);result = 0;for i = 1:nterm = y(i);for j = 1:nif j ~= iterm = term * (xi - x(j)) / (x(i) - x(j));endendresult = result + term;end
end% 牛顿差商方法函数
function result = newton_interpolation(x, y, xi)n = length(x);f = zeros(n, n);f(:, 1) = y';for j = 2:nfor i = 1:n-j+1f(i, j) = (f(i+1, j-1) - f(i, j-1)) / (x(i+j-1) - x(i));endendresult = f(1, 1);for j = 2:nterm = 1;for i = 1:j-1term = term * (xi - x(i));endresult = result + f(1, j) * term;end
end
- 结果:
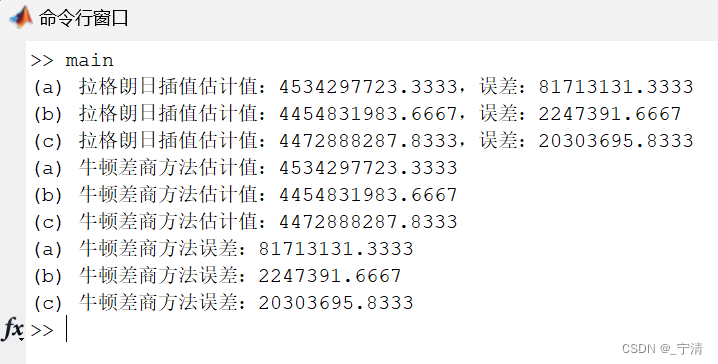
插值多项式次数越高,并不意味着近似结果一定越好。在插值中存在一个称为过拟合的问题,即使用高次多项式拟合数据,可能在已知数据点上表现得非常好,但在未知数据点上可能表现不佳。高次多项式在插值过程中容易产生振荡,尤其是在数据点边缘附近。这种情况下,多项式可能在数据点之间产生大的振荡,而不是真实的趋势。
- 按(a)(b)(c)的具体要求给出结果即可。
-
(a)&(b):
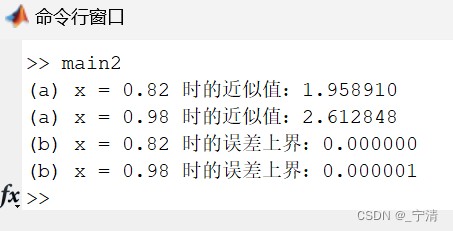
-
©:
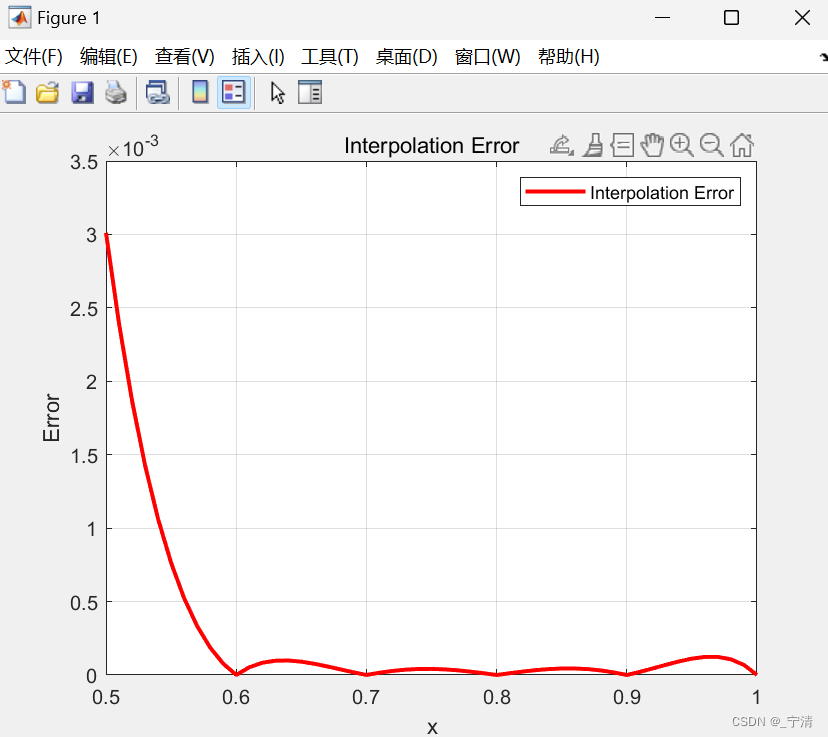
六、总结与思考
在实现拉格朗日插值和牛顿差商插值之前,深入理解了插值的基本原理是关键。插值的目标是通过已知数据点构建一个多项式,使得这个多项式在这些点上与真实函数相等。拉格朗日插值和牛顿差商插值是两种常见的插值方法,它们都基于多项式的性质,通过给定的插值节点生成插值多项式。
在编写和调试代码的过程中,遇到了一些错误,例如矩阵乘法的维度问题。这提醒了我在编写代码时要特别注意矩阵和数组的维度匹配,以避免出现运行时错误。同时,对于 MATLAB 的一些特殊语法和操作,要时刻保持警惕。
这次实验让我更深入地了解了插值方法的原理和应用,提高了对插值误差的理解。实践中遇到的问题促使我更加注重代码的细节和调试过程。通过这次实验,我对 MATLAB 编程、插值算法和数值计算的知识有了更全面的认识。在以后的学习和实践中,我将更加注重理论和实际问题的结合,提高编程和问题解决的能力。
相关文章:

拉格朗日插值及牛顿差商方法的实现(Matlab)
一、问题描述 拉格朗日插值及牛顿差商方法的实现。 二、实验目的 掌握拉格朗日插值和牛顿差商方法的原理,能够编写代码实现两种方法;能够分析多项式插值中的误差。 三、实验内容及要求 利用拉格朗日插值及牛顿差商方法估计1980 年的人口,并…...

【InternLM实战营第二期笔记】02:大模型全链路开源体系与趣味demo
文章目录 00 环境设置01 部署一个 chat 小模型作业一 02 Lagent 运行 InternLM2-chat-7B运行一个工具调用解方程 03 浦语灵笔2进阶作业 第二节课程视频与文档: https://www.bilibili.com/video/BV1AH4y1H78d/ https://github.com/InternLM/Tutorial/blob/camp2/hell…...
Postgresql源码(134)优化器针对volatile函数的排序优化分析
相关 《Postgresql源码(133)优化器动态规划生成连接路径的实例分析》 上一篇对路径的生成进行了分析,通过make_one_rel最终拿到了一个带着路径的RelOptInfo。本篇针对带volatile函数的排序场景继续分析subquery_planner的后续流程。 subquer…...

DES加密算法笔记
【DES加密算法|密码学|信息安全】https://www.bilibili.com/video/BV1KQ4y127AT?vd_source7ad69e0c2be65c96d9584e19b0202113 根据此视频学习 DES是对称密码中的分组加密算法 (分组加密对应流加密算法) 流加密算法就是一个字节一个字节加密 分组加…...

C语⾔:内存函数
1. memcpy使⽤和模拟实现(对内存块的复制,不在乎类型) void * memcpy ( void * destination, const void * source, size_t num ); • 函数memcpy从source的位置开始向后复制num个字节的数据到destination指向的内存位置。 • 这个函数在遇…...
SqliSniper:针对HTTP Header的基于时间SQL盲注模糊测试工具
关于SqliSniper SqliSniper是一款基于Python开发的强大工具,该工具旨在检测HTTP请求Header中潜在的基于时间的SQL盲注问题。 该工具支持通过多线程形式快速扫描和识别目标应用程序中的潜在漏洞,可以大幅增强安全评估过程,同时确保了速度和效…...

3W 1.5KVDC 隔离 宽范围输入,双隔离双输出 DC/DC 电源模块——TPD-3W系列
TPD-3W系列产品是专门针对线路板上分布式电源系统中需要产生一组与输入电源隔离的双隔离双电源的应用场合而设计。该产品适用于:1)输入电源的电压变化范围≤2:1 ;2)输入输出之间要求隔离≤1500VDC;3&#x…...
[java基础揉碎]文件IO流
目录 文件 什么是文件 文件流编辑 常用的文件操作 创建文件方式一 创建文件方式二 创建文件方式三 tip:为什么new file 了还有执行createNewFile?new File的时候其实是在内存中创建了文件对象, 还没有在磁盘中, 当执行createNewFile的时候才是往磁盘中写入编辑 …...
)
[面经] 西山居非正式面试(C++)
前言 这次面试是我第一次面试,而且我也并没有做好准备,应该说几乎就是临场发挥,面试的时间与我推测的相差太大,几乎就是做完简历的下一天就马上去面试了,有不少地方自己没能很好的答出,故做此记录。 关于…...
SOLIDWORKS教育版代理商应该如何选择?
SOLIDWORKS作为目前流行的三维设计软件在工程设计,制造和建筑中有着广泛的应用前景。教育版SOLIDWORKS软件是学生及教育机构学习教学的理想平台。 下面介绍几个挑选SOLIDWORKS教育版代理的关键要素: 1、专业知识与经验:代理商应掌握SOLIDWORKS等软件的丰…...
翻译《Use FILE_SHARE_DELETE in your shell extension》
在写 《翻译《The Old New Thing》- What did MakeProcInstance do?》 文章时,了解到了 Michael Geary ,他也有不少优秀的技术文章,现翻译一篇关于文件操作的细节的文章 原文 Use FILE_SHARE_DELETE in your shell extension | mg.tohttps:…...

使用Python发送电子邮件
大家好,当我们需要迅速、方便地与他人沟通时,电子邮件是无疑是一种不可或缺的通信工具。无论是在个人生活中还是工作场合,电子邮件都是我们日常生活中的重要组成部分。它不仅能够传递文字信息,还可以发送附件、链接和嵌入式多媒体…...
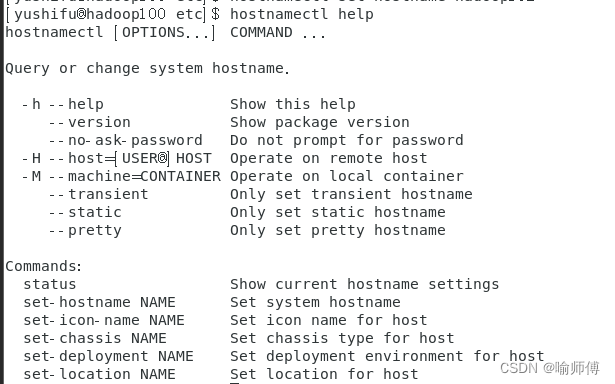
Linux-CentOS7-解决vim修改不了主机名称(无法打开并写入文件)
Linux-CentOS7-修改主机名称 修改之后使用强制保存退出也不行。 解决办法: 使用hostnamectl命令进行修改 查看系统主机名和信息: hostnamectl这条命令会显示当前系统的主机名、操作系统信息、内核版本、架构信息等相关信息。 修改系统主机名࿱…...
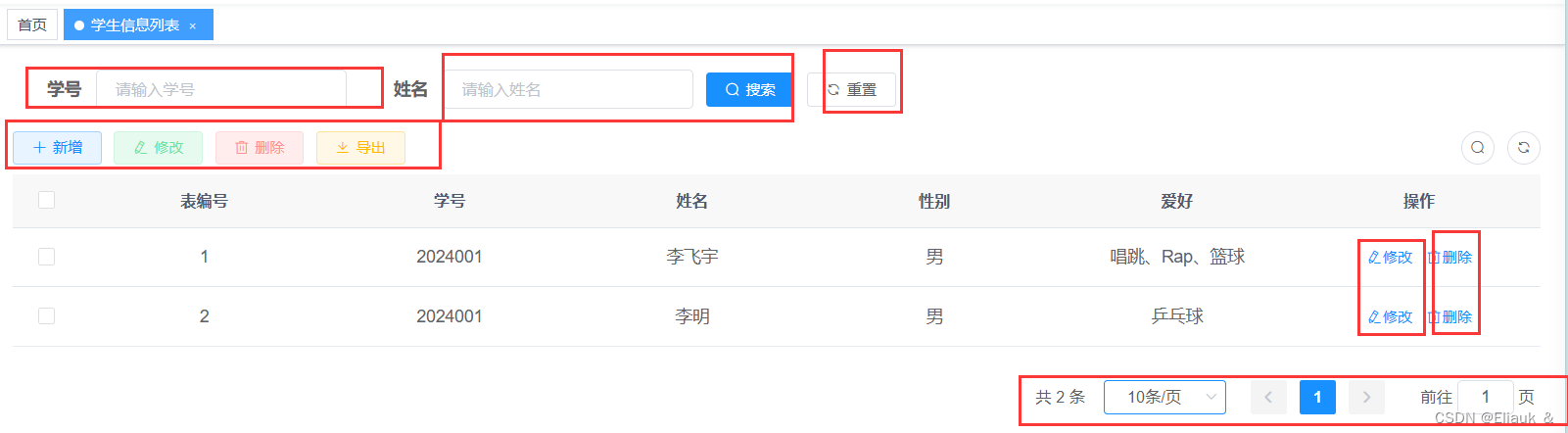
【RuoYi】使用代码生成器完成CRUD操作
一、前言 前面,介绍了如何下载和启动我们的RuoYi框架。为了让小伙伴们认识到ruoyi的强大,那么这篇博客就介绍一下如何使用ruoyi的代码生成器,自动生成前端页面以及后端的对应数据库表的CRUD操作!!!真的很强…...

七个很酷的GenAI LLM技术性面试问题
不同于互联网上随处可见的传统问题库,这些问题需要跳出常规思维。 大语言模型(LLM)在数据科学、生成式人工智能(GenAI)和人工智能领域越来越重要。这些复杂的算法提升了人类的技能,并在诸多行业中推动了效率和创新性的提升,成为企业保持竞争…...

SARscape雷达图像处理软件简介
合成孔径雷达(SAR)拥有独特的技术魅力和优势,渐成为国际上的研究热点之一,其应用领域越来越广泛。SAR数据可以全天候对研究区域进行量测、分析以及获取目标信息。高级雷达图像处理工具SARscape,能让您轻松将原始SAR数据…...

开源博客项目Blog .NET Core源码学习(23:App.Hosting项目结构分析-11)
本文学习并分析App.Hosting项目中后台管理页面的标签管理页面、轮播图维护页面。 标签管理页面 标签管理页面用于显示、检索、新建、编辑、删除标签数据,以便在前台页面的首页及文章专栏等页面显示标签数据。标签管理页面附带一新建及编辑页面,以支撑新…...

一.ffmpeg 将内存中的H264跟PCM 数据流合成多媒体文件
在有一些嵌入式平台中,H264数据流一般来自芯片内部的硬编码器, AAC音频数据则是通过采集PCM进行软编码,但是如何对它实时进行封装多媒体文件 ,参考ffmpeg example,花了一些时间终于实现了该功能。 流程图如下…...

C++ (week5):Linux系统编程3:线程
文章目录 三、线程1.线程的基本概念①线程相关概念②我的理解 2.线程的基本操作 (API)(1)获取线程的标识:pthread_self(2)创建线程:pthread_create()(3)终止线程①pthread_exit():当前线程终止,子线程主动退出②pthread_cancel()&…...
二叉树习题精讲-相同的树
相同的树 100. 相同的树 - 力扣(LeetCode)https://leetcode.cn/problems/same-tree/description/ /*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ bool i…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
