代码随想录算法训练营Day54 | 392.判断子序列、115.不同的子序列 | Python | 个人记录向
本文目录
- 392.判断子序列
- 做题
- 看文章
- 115.不同的子序列
- 做题
- 看文章
- 以往忽略的知识点小结
- 个人体会
392.判断子序列
代码随想录:392.判断子序列
Leetcode:392.判断子序列
做题
借鉴Day53中1143.最长公共子序列的思路,最后改一下判断逻辑即可。
class Solution:def isSubsequence(self, s: str, t: str) -> bool:dp = [[0] * (len(s)+1) for _ in range(len(t)+1)]for i in range(1, len(t)+1):for j in range(1, len(s)+1):if t[i-1] == s[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = max(dp[i][j-1], dp[i-1][j])if dp[len(t)][len(s)] == len(s):return Trueelse:return False
时间复杂度:O(n × m)
空间复杂度:O(n × m)
看文章
思路一致。
115.不同的子序列
代码随想录:115.不同的子序列
Leetcode:115.不同的子序列
做题
无思路。
看文章
这道题很难,题解也看了很久。
动规五部曲:
-
确定dp数组(dp table)以及下标的含义。
dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
-
确定递推公式。这一类问题,基本是要分析两种情况:
s[i - 1] 与 t[j - 1]相等,dp[i][j]可以有两部分组成。
一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母,所以只需要 dp[i-1][j-1]。
另一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j],相当于复制直接的结果。s[i - 1] 与 t[j - 1] 不相等,dp[i][j]只有一部分组成,不用s[i - 1]来匹配(就是模拟在s中删除这个元素),即:dp[i - 1][j]。
-
dp数组如何初始化。
dp[i][0]:以i-1为结尾的s可以随便删除元素,出现空字符串的个数。那么dp[i][0]一定都是1,因为也就是把以i-1为结尾的s,删除所有元素,出现空字符串的个数就是1。
dp[0][j]:空字符串s可以随便删除元素,出现以j-1为结尾的字符串t的个数。那么dp[0][j]一定都是0,s如论如何也变成不了t。
-
确定遍历顺序。
外部遍历 s,内部遍历 t。
-
举例推导dp数组。
代码如下:
class Solution:def numDistinct(self, s: str, t: str) -> int:dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]for i in range(len(s)+1):dp[i][0] = 1for i in range(1, len(s)+1):for j in range(1, len(t)+1):if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + dp[i-1][j]else:dp[i][j] = dp[i-1][j]return dp[len(s)][len(t)]
以往忽略的知识点小结
- 回到动规五部曲的基本思路,特别是dp数组的含义
个人体会
完成时间:1h30min。
心得:115.不同的子序列比较难,看了好久,需要回归到动规五部曲的基本思路,特别是dp数组的含义。
相关文章:

代码随想录算法训练营Day54 | 392.判断子序列、115.不同的子序列 | Python | 个人记录向
本文目录 392.判断子序列做题看文章 115.不同的子序列做题看文章 以往忽略的知识点小结个人体会 392.判断子序列 代码随想录:392.判断子序列 Leetcode:392.判断子序列 做题 借鉴Day53中1143.最长公共子序列的思路,最后改一下判断逻辑即可。…...
提升多表联查速度)
利用oracle默认事务隔离级别(提交读)提升多表联查速度
利用oracle默认事务隔离级别(提交读)提升查询速度) 背景介绍: 数据量大查询缓慢,添加太多条件,使用IN走了全表查询导致查询速度缓慢。 解决方案: 版本一: 新建临时表,在查询是将数据插入到临时表中&#…...
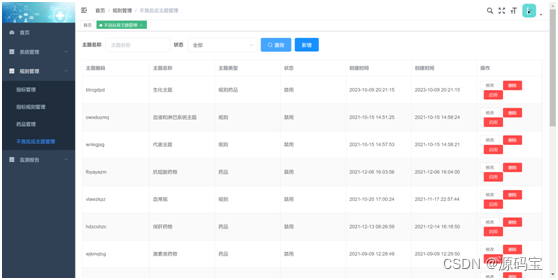
B/S架构+java语言+Mysqladr数 据 库ADR药物不良反应监测系统源码 ADR药物不良反应监测系统有哪些作用?
B/S架构+java语言+Mysqladr数 据 库ADR药物不良反应监测系统源码 ADR药物不良反应监测系统有哪些作用? 药物不良反应(ADR)是指在合格药物以正常用量和用法用于预防、诊断、治疗疾病或调节生理功能时所发生的意外的、与防治目的无关的、不利或…...

Matlab中% note that Wilkinson notation (‘L1~L4~1‘) is used to specify the model
fitrm 函数的输入参数不正确,似乎出错的地方是在定义 fitrm 对象时使用了不正确的参数。 fitrm 函数的语法是这样的: rm fitrm(tbl, model, WithinDesign, withinDesign) 其中: - tbl 是一个表格,包含了待分析的数据。 - mod…...

测试测试测试
一分钟速览新闻点! 京东前副总裁蔡磊回应被指装病:没有时间、精力和能力应对 百度沈抖:主力模型免费的原因很朴素,希望大家别再天天拉表格比价格 蚂蚁集团CTO何征宇:蚂蚁一直在努力优化和提高AI的可靠性、经济性和易…...

动态规划专题
leecode 221 class Solution { public:int maximalSquare(vector<vector<char>>& matrix) {int n matrix.size();if (n 0) return 0; // 如果矩阵为空,则直接返回0 int m matrix[0].size();vector<vector<int>> ans(n, vector<i…...
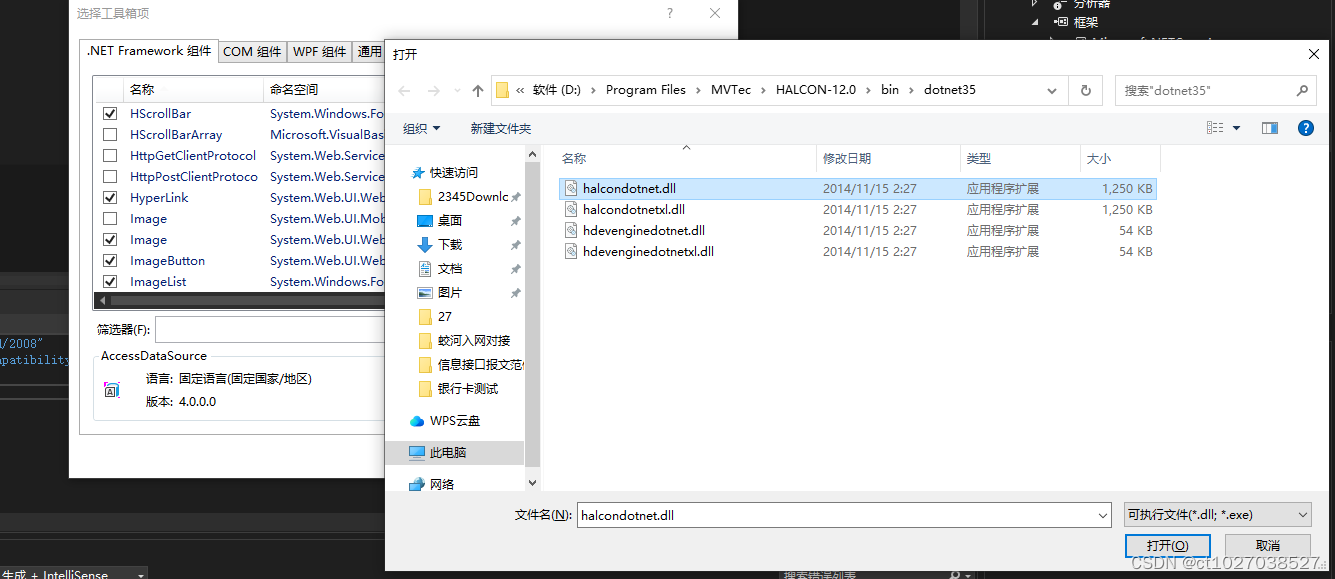
.net8.0与halcon编程环境构建
1.安装vs2022 2.安装h-12.0.exe ,不要勾选复选框 3.vs2022新建wpf应用程序 4.依赖项添加项目应用,选择halcondotnet.dll 5.安装System.Drawing 安装 HalconDotNet 安装 Rti.HDevEngineDotNet 在工具箱 空白处右键 应用halcon.dll WPF控件也应用halcon.dll 6.xaml申明hal…...
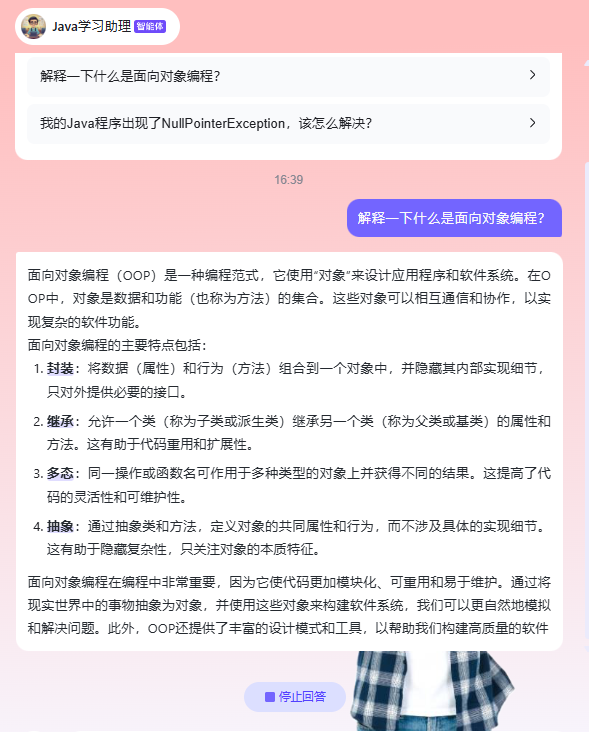
文心智能体平台:快来创建你的Java学习小助理,全方位辅助学习
文章目录 一、文心智能体平台1.1平台介绍1.2智能体介绍 二、智能体创建三、体验与总结 一、文心智能体平台 文心智能体平台是百度推出的基于文心大模型的智能体(Agent)平台,支持广大开发者根据自身行业领域、应用场景,选取不同类…...

AppInventor2 表格布局的外面的黑框怎么去掉?
问:表格布局的外面的黑框怎么去掉啊? 答:这个黑框是界面设计的布局位置示意,实际 App 测试时并没有框。 来源:AppInventor2 表格布局的外面的黑框怎么去掉? - App应用开发 - 清泛IT社区,为创新…...

爬楼梯(进阶版)
思路: 没什么难的,就是一个排序的01背包问题,秒了 #include<bits/stdc.h> using namespace std;int n,m; int main(){cin>>n>>m;vector<int>dp(2000,0);dp[0]1;for(int i0;i<n;i){for(int j1;j<m;j){if(i>…...

echarts-事件
echarts部分事件 添加点击事件 添加点击事件: let options {tooltip: {},xAxis: {type: "category",data: ["d1", "d2", "d3", "d4"],},yAxis: {},series: [{type: "line",data: d1,},{type: &qu…...
备受推崇的公司文件加密文件推荐榜单
迄今为止,加密依然是最有效的用于保护数据、通讯安全的手段之一 在数字化时代,文件加密软件成为了保护个人和企业数据安全的重要工具。随着技术的不断进步,市场上涌现出了众多优秀的文件加密软件。 以下十款文件加密软件因其出色的性能、易…...

QT——QSlider实现,QT滑动控件的使用
目录 简介滑动块调节两种方法滑动条触发信号量理想滑动块运用(参考) 简介 QT中滑动条的控件叫QSlider,继承自QAbstractSlider类。 主要用途是通过滑块的滑动的方式在一定范围内调节某个值。根据调节的后得到的结果去执行一些处理,…...
【网络协议Http】Http中get,post,put,delete区别
Http协议 超文本传输协议(Hypertext Transfer Protocol,HTTP)是一个简单的请求-响应协议,它通常运行在TCP之上。 【参考】 GET && POST 对比 关于tcp数据包:对于GET方式的请求,浏览器会把http hea…...

软硬中断区别,磁盘块、扇区、页区别与之间的关系
软硬中断: 软中断是执行中断指令产生的,而硬中断是由外设引发的。 硬中断的中断号是由中断控制器提供的,软中断的中断号由指令直接指出,无需使用中断控制器。 硬中断是可屏蔽的,软中断不可屏蔽。 硬中断处理程序要…...
在线思维导图编辑!3个AI思维导图生成软件推荐!
思维导图,一种以创新为驱动的视觉化思考工具,已经渗透到我们日常生活和工作的各个角落。当我们需要整理思绪、规划项目或者梳理信息时,思维导图总能提供极大的帮助。 近些年随着云服务等基础设施的完善,我们可以看到越来越多提供…...

使用 Ubuntu + Docker + Vaultwarden + Tailscale 自建密码管理器
使用 Ubuntu Docker Vaultwarden Tailscale 自建密码管理器 先决条件 一台运行 Ubuntu 系统的服务器。可以是云提供商的 VPS、家庭网络中的树莓派、或者 Windows 电脑上的虚拟机等等 一个 Tailscale 账户。如果还没有 Tailscale 账户,可以通过此链接迅速创建一个…...

YOLOv7添加注意力机制和各种改进模块
YOLOv7添加注意力机制和各种改进模块代码免费下载:完整代码 添加的部分模块代码: ########CBAM class ChannelAttentionModule(nn.Module):def __init__(self, c1, reduction16):super(ChannelAttentionModule, self).__init__()mid_channel c1 // red…...

【OpenGL第一个程序】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、OpenGL第一个程序 前言 本文介绍了OpenGL入门的第一个程序,有详细的注释,便于大家理解其中的逻辑。 一、OpenGL第一个程序 #inclu…...
GPT-4O神器来袭!自动生成Figma设计稿,移动端开发瞬间加速!
2024年5月29日- 近日,一款基于GPT-4O技术的创新工具成功实现根据产品需求文档(PRD)自动生成Figma设计稿的功能,为移动端应用开发者带来革命性的便捷。据悉,该功能主要针对移动端应用进行优化,并支持使用高质…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
