Matlab中% note that Wilkinson notation (‘L1~L4~1‘) is used to specify the model
`fitrm` 函数的输入参数不正确，似乎出错的地方是在定义 `fitrm` 对象时使用了不正确的参数。
`fitrm` 函数的语法是这样的：
rm = fitrm(tbl, model, 'WithinDesign', withinDesign)
其中：
- `tbl` 是一个表格，包含了待分析的数据。
- `model` 是一个字符向量，用来指定模型，例如 `'y ~ x1 + x2'`。
- `withinDesign` 是一个设计矩阵，用来指定实验设计。
`tabl_temp` 是你的数据表，`'L1-L4~1'` 是模型，而 `measure3` 可能是你为实验设计定义的一些内容。但是由于错误信息不够详细，很难确定问题的具体原因。
1. 确保 `tabl_temp` 是一个正确的表格，并且包含你需要的数据。
2. 检查模型的定义是否正确。确保使用的是有效的语法，并且模型中的变量在 `tabl_temp` 中是存在的。
3. 检查实验设计 (`withinDesign`) 的定义是否正确。
相关文章：
Matlab中% note that Wilkinson notation (‘L1~L4~1‘) is used to specify the model
fitrm 函数的输入参数不正确，似乎出错的地方是在定义 fitrm 对象时使用了不正确的参数。 fitrm 函数的语法是这样的： rm fitrm(tbl, model, WithinDesign, withinDesign) 其中： - tbl 是一个表格，包含了待分析的数据。 - mod…...
测试测试测试
一分钟速览新闻点！ 京东前副总裁蔡磊回应被指装病：没有时间、精力和能力应对 百度沈抖：主力模型免费的原因很朴素，希望大家别再天天拉表格比价格 蚂蚁集团CTO何征宇：蚂蚁一直在努力优化和提高AI的可靠性、经济性和易…...
动态规划专题
leecode 221 class Solution { public:int maximalSquare(vector<vector<char>>& matrix) {int n matrix.size();if (n 0) return 0; // 如果矩阵为空，则直接返回0 int m matrix[0].size();vector<vector<int>> ans(n, vector<i…...
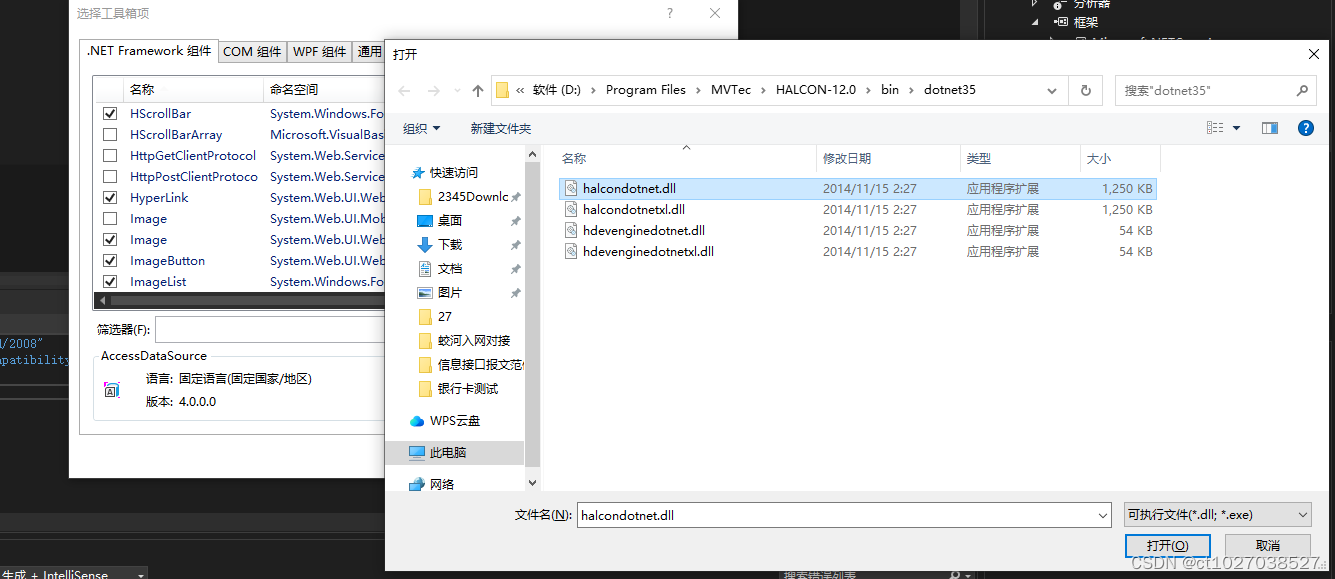
.net8.0与halcon编程环境构建
1.安装vs2022 2.安装h-12.0.exe ，不要勾选复选框 3.vs2022新建wpf应用程序 4.依赖项添加项目应用，选择halcondotnet.dll 5.安装System.Drawing 安装 HalconDotNet 安装 Rti.HDevEngineDotNet 在工具箱 空白处右键 应用halcon.dll WPF控件也应用halcon.dll 6.xaml申明hal…...
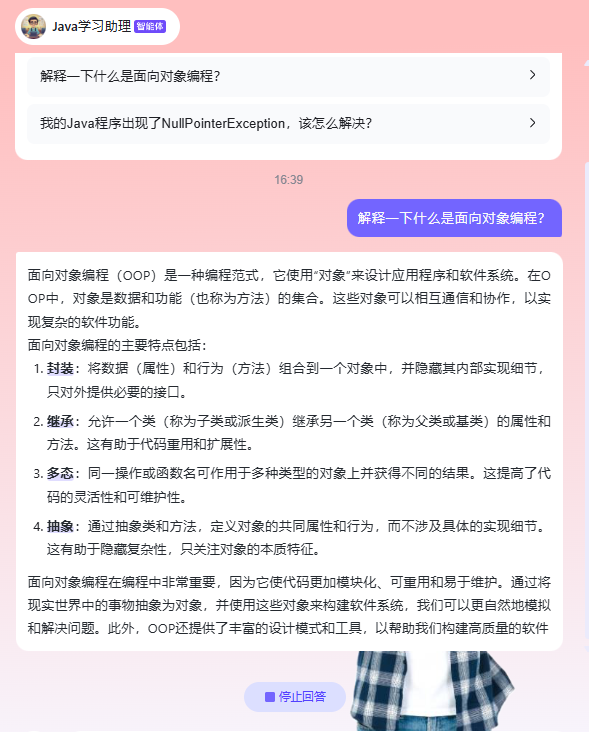
文心智能体平台：快来创建你的Java学习小助理，全方位辅助学习
文章目录 一、文心智能体平台1.1平台介绍1.2智能体介绍 二、智能体创建三、体验与总结 一、文心智能体平台 文心智能体平台是百度推出的基于文心大模型的智能体（Agent）平台，支持广大开发者根据自身行业领域、应用场景，选取不同类…...
AppInventor2 表格布局的外面的黑框怎么去掉？
问：表格布局的外面的黑框怎么去掉啊？ 答：这个黑框是界面设计的布局位置示意，实际 App 测试时并没有框。 来源：AppInventor2 表格布局的外面的黑框怎么去掉？ - App应用开发 - 清泛IT社区，为创新…...
爬楼梯（进阶版）
思路： 没什么难的，就是一个排序的01背包问题，秒了 #include<bits/stdc.h> using namespace std;int n,m; int main(){cin>>n>>m;vector<int>dp(2000,0);dp[0]1;for(int i0;i<n;i){for(int j1;j<m;j){if(i>…...
echarts-事件
echarts部分事件 添加点击事件 添加点击事件： let options {tooltip: {},xAxis: {type: "category",data: ["d1", "d2", "d3", "d4"],},yAxis: {},series: [{type: "line",data: d1,},{type: &qu…...
备受推崇的公司文件加密文件推荐榜单
迄今为止，加密依然是最有效的用于保护数据、通讯安全的手段之一 在数字化时代，文件加密软件成为了保护个人和企业数据安全的重要工具。随着技术的不断进步，市场上涌现出了众多优秀的文件加密软件。 以下十款文件加密软件因其出色的性能、易…...
QT——QSlider实现，QT滑动控件的使用
目录 简介滑动块调节两种方法滑动条触发信号量理想滑动块运用（参考） 简介 QT中滑动条的控件叫QSlider，继承自QAbstractSlider类。 主要用途是通过滑块的滑动的方式在一定范围内调节某个值。根据调节的后得到的结果去执行一些处理，…...
【网络协议Http】Http中get，post，put，delete区别
Http协议 超文本传输协议（Hypertext Transfer Protocol，HTTP）是一个简单的请求-响应协议，它通常运行在TCP之上。 【参考】 GET && POST 对比 关于tcp数据包：对于GET方式的请求，浏览器会把http hea…...
软硬中断区别，磁盘块、扇区、页区别与之间的关系
软硬中断： 软中断是执行中断指令产生的，而硬中断是由外设引发的。 硬中断的中断号是由中断控制器提供的，软中断的中断号由指令直接指出，无需使用中断控制器。 硬中断是可屏蔽的，软中断不可屏蔽。 硬中断处理程序要…...
在线思维导图编辑！3个AI思维导图生成软件推荐！
思维导图，一种以创新为驱动的视觉化思考工具，已经渗透到我们日常生活和工作的各个角落。当我们需要整理思绪、规划项目或者梳理信息时，思维导图总能提供极大的帮助。 近些年随着云服务等基础设施的完善，我们可以看到越来越多提供…...
使用 Ubuntu + Docker + Vaultwarden + Tailscale 自建密码管理器
使用 Ubuntu Docker Vaultwarden Tailscale 自建密码管理器 先决条件 一台运行 Ubuntu 系统的服务器。可以是云提供商的 VPS、家庭网络中的树莓派、或者 Windows 电脑上的虚拟机等等 一个 Tailscale 账户。如果还没有 Tailscale 账户，可以通过此链接迅速创建一个…...
YOLOv7添加注意力机制和各种改进模块
YOLOv7添加注意力机制和各种改进模块代码免费下载：完整代码 添加的部分模块代码： ########CBAM class ChannelAttentionModule(nn.Module):def __init__(self, c1, reduction16):super(ChannelAttentionModule, self).__init__()mid_channel c1 // red…...
【OpenGL第一个程序】
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 前言一、OpenGL第一个程序 前言 本文介绍了OpenGL入门的第一个程序，有详细的注释，便于大家理解其中的逻辑。 一、OpenGL第一个程序 #inclu…...
GPT-4O神器来袭！自动生成Figma设计稿，移动端开发瞬间加速！
2024年5月29日- 近日，一款基于GPT-4O技术的创新工具成功实现根据产品需求文档（PRD）自动生成Figma设计稿的功能，为移动端应用开发者带来革命性的便捷。据悉，该功能主要针对移动端应用进行优化，并支持使用高质…...
清华大学提出IFT对齐算法，打破SFT与RLHF局限性
监督微调（Supervised Fine-Tuning, SFT）和基于人类反馈的强化学习（Reinforcement Learning from Human Feedback, RLHF）是预训练后提升语言模型能力的两大基础流程，其目标是使模型更贴近人类的偏好和需求。 考虑到监督…...
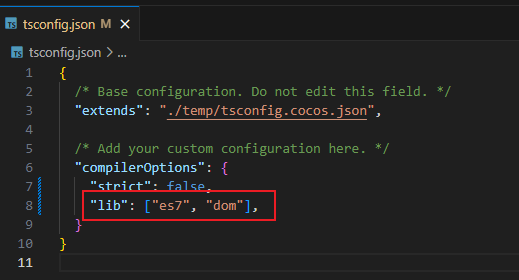
TS（TypeScript）中Array数组无法调出使用includes方法，显示红色警告
解决方法 打开tsconfig.json文件，添加"lib": ["es7", "dom"]即可。 如下图所示。...
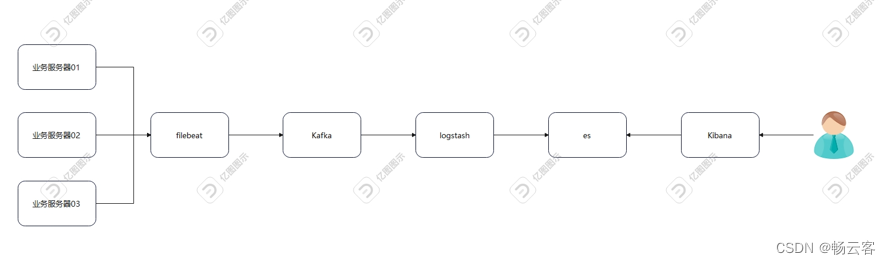
基于Kafka的日志采集
目录 前言 架构图 资源列表 基础环境 关闭防护墙 关闭内核安全机制 修改主机名 添加hosts映射 一、部署elasticsearch 修改limit限制 部署elasticsearch 修改配置文件 启动 二、部署filebeat 部署filebeat 添加配置文件 启动 三、部署kibana 部署kibana 修…...
[特殊字符] 智能合约中的数据是如何在区块链中保持一致的？
🧠 智能合约中的数据是如何在区块链中保持一致的？ 为什么所有区块链节点都能得出相同结果？合约调用这么复杂，状态真能保持一致吗？本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上，你可以使用apt包管理器来安装NFS服务器。打开终端并运行： sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享，例如/shared： sudo mkdir /shared sud…...
反射获取方法和属性
Java反射获取方法 在Java中，反射（Reflection）是一种强大的机制，允许程序在运行时访问和操作类的内部属性和方法。通过反射，可以动态地创建对象、调用方法、改变属性值，这在很多Java框架中如Spring和Hiberna…...
关键领域软件测试的突围之路：如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天，软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件，这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下，实现高效测试与快速迭代？这一命题正考验着…...
10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI，使用客户端或是内部自己搭建集成大模型的终端，加速与大型语言模型（LLM）的结合，同时使用检索增强生成（Retrieval Augmented Generation &#…...
2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师（题目+回答）
安全领域各种资源，学习文档，以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具，欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
DeepSeek越强，Kimi越慌？
被DeepSeek吊打的Kimi，还有多少人在用？ 去年，月之暗面创始人杨植麟别提有多风光了。90后清华学霸，国产大模型六小虎之一，手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水，单月光是投流就花费2个亿。 疯…...
CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection（反射） 这个概念，总结一下： Reflection（反射）是什么？ 反射是对类型的自我检查能力（Introspection） 可以查看类的成员变量、成员函数等信息。反射允许枚…...