P2341 受欢迎的牛
题目描述
每一头牛的愿望就是变成一头最受欢迎的牛。现在有 N 头牛,给你 M 对整数,表示牛 A 认为牛 B 受欢迎。这种关系是具有传递性的,如果 A 认为 B 受欢迎,B 认为 C 受欢迎,那么牛 A 也认为牛 C 受欢迎。你的任务是求出有多少头牛被除自己之外的所有牛认为是受欢迎的。
输入描述
第一行两个数 N,M;
接下来 M 行,每行两个数 A,B,意思是 A 认为 B 是受欢迎的(给出的信息有可能重复,即有可能出现多个 A,B)。
输出描述
输出被除自己之外的所有牛认为是受欢迎的牛的数量。
样例输入
3 3 1 2 2 1 2 3
样例输出
1
我们先把这道题分成两种情况来讨论
第一种情况:不存在环
首先来画一个图

观察一下每个点的出度
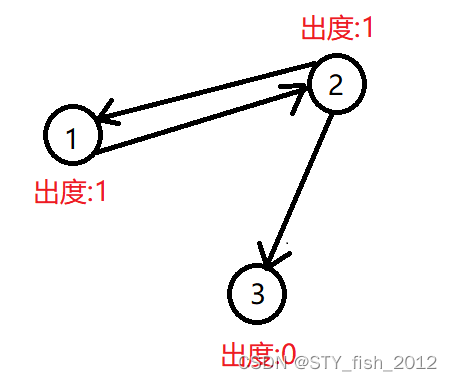
在这幅图中,最受欢迎的牛是3, 那么,是否是出度为零的点就最受欢迎呢?
再来看一下

此时,点4的出度也为零,但是,这张图没有最受欢迎的牛,因为条件是除自己以外,所有人都认为它受欢迎才行,所以,在没有环情况下,如果只有一个出度为零的点,就有一头最受欢迎的牛,否则一头都没有
再来看第二种情况
第二种情况:存在环
还是来画张图
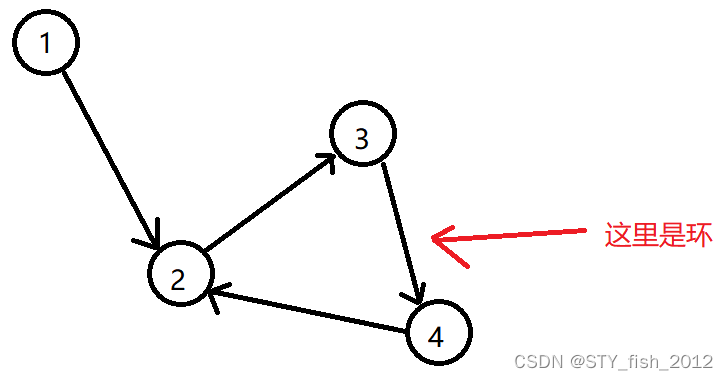
这里最受欢迎的是2,3,4
结论:有环时,先把每一个环合并成一个点,在按照没有环的方案去找,最后最受欢迎的就是那个点合并前的所有点
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+5;
vector<int>a[N];
int dfn[N],vis[N],id[N],size[N],low[N],cd[N];
int n,m;
int times;
int scc;
stack<int>t;
void tarjan(int x){vis[x]=1;dfn[x]=low[x]=++times;t.push(x);for(int i=0;i<a[x].size();i++){int v=a[x][i];if(dfn[v]==0){tarjan(v);low[x]=min(low[x],low[v]);}else if(vis[v]==1){low[x]=min(low[x],dfn[v]);}}if(low[x]==dfn[x]){scc++;int v;do{v=t.top();t.pop();vis[v]=0;id[v]=scc;size[scc]++;}while(x!=v);}
}
main(){scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);a[u].push_back(v);}for(int i=1;i<=n;i++){if(dfn[i]==0)tarjan(i);}for(int x=1;x<=n;x++){for(int i=0;i<a[x].size();i++){int v=a[x][i];int u1=id[x];int u2=id[v];if(u1!=u2){cd[u1]++;}}}int cnt=0,ans=0;for(int i=1;i<=scc;i++){if(cd[i]==0){ans+=size[i];cnt++;if(cnt>1){printf("0");return 0;}}}printf("%d",ans);
}相关文章:

P2341 受欢迎的牛
题目描述 每一头牛的愿望就是变成一头最受欢迎的牛。现在有 N 头牛,给你 M 对整数,表示牛 A 认为牛 B 受欢迎。这种关系是具有传递性的,如果 A 认为 B 受欢迎,B 认为 C 受欢迎,那么牛 A 也认为牛 C 受欢迎。你的任务是…...
Linux系统编程(五)多线程
目录 一、基本知识点二、线程的编译三、 线程相关函数1. 线程的创建2. 线程的退出3. 线程的等待补充 四、综合举例 一、基本知识点 线程(Thread)是操作系统能够进行运算调度的最小单位。它被包含在进程之中,是进程中的实际运作单位。一个标准…...

HTTP Basic Access Authentication Schema
HTTP Basic Access Authentication Schema 背景介绍流程安全缺陷参考 背景 本文内容大多基于网上其他参考文章及资料整理后所得,并非原创,目的是为了需要时方便查看。 介绍 HTTP Basic Access Authentication Schema,HTTP 基本访问认证模式…...

#职场发展#其他
一闪论文是目前市场上一款非常靠谱的论文写作工具,不仅可以帮助用户快速完成论文撰写,还能对文章进行查重降重,确保内容原创性。从用户的角度来看,一闪论文确实是一个非常方便、实用的工具,能够大大提高写作效率&#…...

【Text2SQL 论文】评估 ChatGPT 的 zero-shot Text2SQL 能力
论文:A comprehensive evaluation of ChatGPT’s zero-shot Text-to-SQL capability ⭐⭐⭐⭐ arXiv:2303.13547 这篇论文呢综合评估了 ChatGPT 在 zero-shot Text2SQL 任务上的表现。 dataset 使用了 Spider、Spider-SYN、Spider-DK、Spider-Realistic、Spider-CG…...

安卓手机APP开发___设置闹钟
安卓手机APP开发___设置闹钟 目录 概述 设置不精确闹钟 在特定时间后发出闹钟 在特定时间范围内触发闹钟 以大致有规律的时间间隔响起重复闹钟 设置精确的闹钟 系统会在未来的某个精确时刻调用精确闹钟。 可能不需要精确闹钟的用例 设置精确闹钟的方法 系统资源消耗…...

如何评价GPT-4o
目录 1.概述 2.对比分析 2.1.版本 2.2.区别 2.2.1.技术方面的差异 2.2.2.性能提升 2.2.3.应用领域扩展 2.2.4.对未来发展的影响 3.技术能力 4.个人感受 1.概述 GPT-4o的发布无疑是人工智能领域的一次重要进展。作为GPT-4的升级版本,GPT-4o不仅在处理速度…...

自定义窗口事件循环系统
1.定义事件类型,mouse,wheel,drag,view。已处理的事件,accept需设置为true,防止重叠热区继续穿透。记录事件生成时间,全局位置和当前帧窗口下位置。 2.定义事件响应系统interactionSystem&…...
)
随机森林算法教程(个人总结)
背景 随机森林(Random Forest)是一种集成学习方法,主要用于分类和回归任务。它通过构建多个决策树并将其结果进行集成,提升模型的准确性和鲁棒性。随机森林在处理高维数据和防止过拟合方面表现出色,是一种强大的机器学…...

解决Android studio 一直提示下载gradle-xxx-all.zip问题
今天用AndroidStdiod打开一个新工程的时候,发现项目一直卡在正在下载gradle-xxx-all.zip的任务上,网络出奇的慢,即使配了VPN也无济于事,于是按照以往经验:将gradle-xxx-all.zip下载到.gradle\gradle\wrapper\dists目录…...

3DEXPERIENCE DELMIA Role: RVN - Robotics Virtual Commissioning Analyst
Discipline: Robotics Role: RVN - Robotics Virtual Commissioning Analyst 通过准确地模拟连接到PLC程序的机器人、设备和传感器,在制造虚拟孪生上执行虚拟调试情景 为任何机器人角色的多周期情景创建传感器,生成和变换零件启用 PLC 程序的虚拟验证和…...
js知识点之闭包
闭包 什么是闭包 闭包,是 JavaScript 中一个非常重要的知识点,也是我们前端面试中较高几率被问到的知识点之一。 打开《JavaScript 高级程序设计》和《 JavaScript 权威指南》,会发现里面针对闭包的解释各执一词,在网络上搜索关…...

LORA微调,让大模型更平易近人
技术背景 最近和大模型一起爆火的,还有大模型的微调方法。 这类方法只用很少的数据,就能让大模型在原本表现没那么好的下游任务中“脱颖而出”,成为这个任务的专家。 而其中最火的大模型微调方法,又要属LoRA。 增加数据量和模…...

LabVIEW全自动样品处理系统有哪些优势?
基于LabVIEW的全自动样品处理系统在现代科研和工业应用中展现出显著的优势,其在数据采集、分析和控制方面的性能使其成为提高效率和精度的理想选择。以下是该系统的详细优势: 高效自动化 LabVIEW的图形化编程语言极大地简化了自动化流程的开发。用户可…...

shell脚本操作http请求的返回值——shell处理json格式数据
日常工作中,我们经常会遇到http请求会返回大量格式固定的数据,而我们只需要其中的一部分,那么怎么提取我们想要的字段呢。 这里会介绍一种用shell脚本处理http请求返回,或者处理json格式数据的方式。 这里我们用到了 jq这个强大的…...

leetcode力扣 300. 最长递增子序列 II
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。 示例 1&#…...

C++_vector简单源码剖析:vector模拟实现
文章目录 🚀1.迭代器🚀2.构造函数与析构函数⚡️2.1 默认构造函数vector()⚡️2.2 vector(int n, const T& value T())⚡️内置类型也有构造函数 ⚡️2.3 赋值重载operator⚡️2.4 通用迭代器拷贝⚡️2.5 vector(initializer_list<T> il)⚡️…...

第3章 数据链路层
王道学习 考纲内容 (一)数据链路层的功能 (二)组帧 (三)差错控制 检错编码;纠错编码 (四)流量控制与可靠传输机制 流量控制、可靠传输与滑动窗口…...

使用OrangePi KunPeng Pro部署AI模型
目录 一、OrangePi Kunpeng Pro简介二、环境搭建三、模型运行环境搭建(1)下载Ollama用于启动并运行大型语言模型(2)配置ollama系统服务(3)启动ollama服务(4)启动ollama(5)查看ollama运行状态四、模型部署(1)部署1.8b的qwen(2)部署2b的gemma(3)部署3.8的phi3(4)部署4b的qwen(5)部…...

SpringMVC 数据映射VC
从 view 层发送请求到Controller,在Controller中获取参数: 在不输入值时会报400,参数错误 在不输入值时num默认为null 没有找到对应标签名称叫nums的,输入任何值时都报400 设置required默认值为false,即使表单没有nums…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
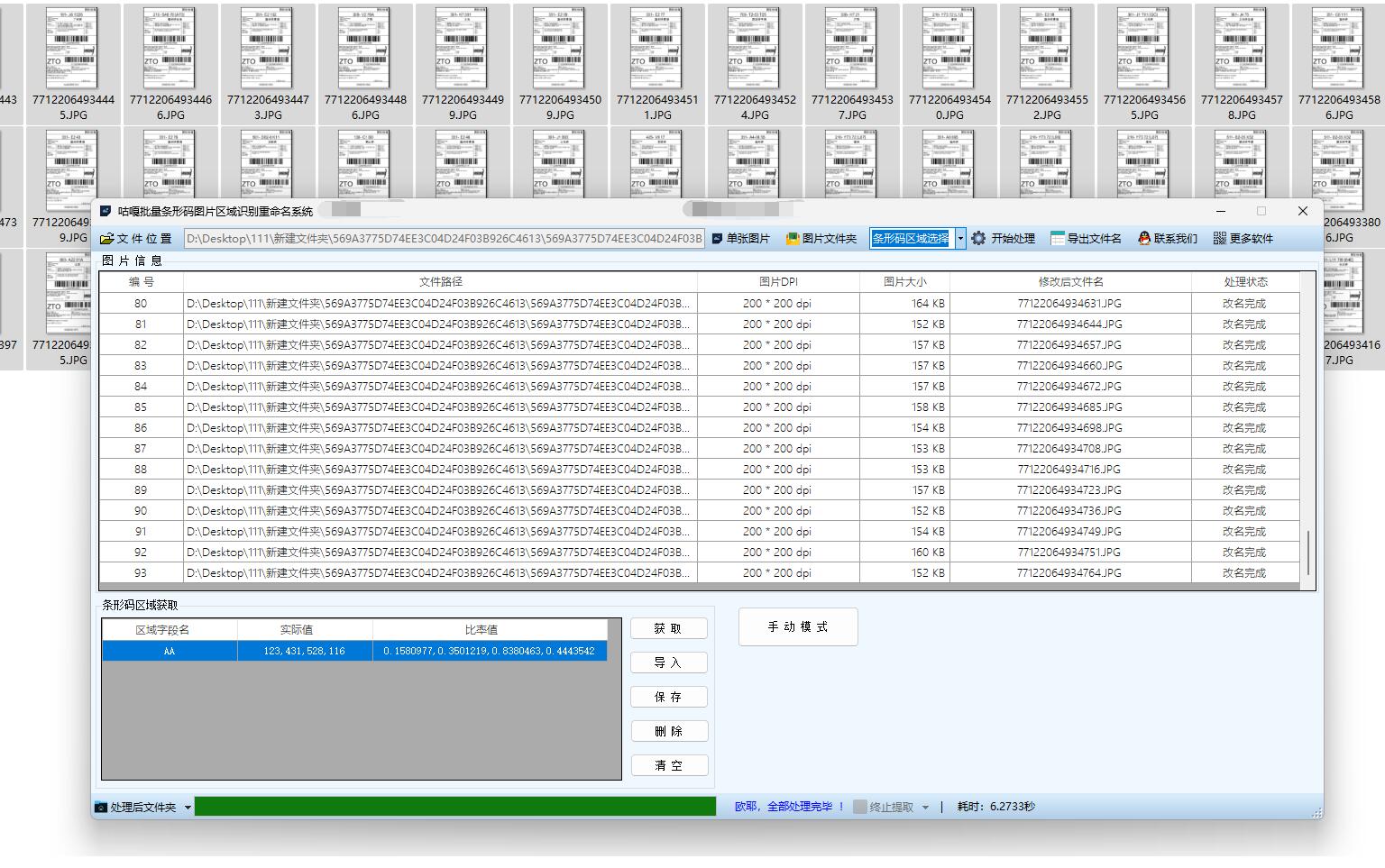
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...

【Redis】Redis从入门到实战:全面指南
Redis从入门到实战:全面指南 一、Redis简介 Redis(Remote Dictionary Server)是一个开源的、基于内存的键值存储系统,它可以用作数据库、缓存和消息代理。由Salvatore Sanfilippo于2009年开发,因其高性能、丰富的数据结构和广泛的语言支持而广受欢迎。 Redis核心特点:…...

从数据报表到决策大脑:AI重构电商决策链条
在传统电商运营中,决策链条往往止步于“数据报表层”:BI工具整合历史数据,生成滞后一周甚至更久的销售分析,运营团队凭经验预判需求。当爆款突然断货、促销库存积压时,企业才惊觉标准化BI的决策时差正成为增长瓶颈。 一…...

如何让非 TCP/IP 协议驱动屏蔽 IPv4/IPv6 和 ARP 报文?
——从硬件过滤到协议栈隔离的完整指南 引言 在现代网络开发中,许多场景需要定制化网络协议(如工业控制、高性能计算),此时需确保驱动仅处理特定协议,避免被标准协议(如 IPv4/IPv6/ARP)干扰。本文基于 Linux 内核驱动的实现,探讨如何通过硬件过滤、驱动层拦截和协议栈…...
