前缀和(下)
目录
热身:
寻找数组的中心下标
题解:
代码:
进阶:
除自身之外数组的乘积
题解:
代码:
和为K的子数组
题解:
代码:
和可被 K 整除的子数组
题解:
同余定理:
为什么需要修正负数取模?
代码:
连续数组
代码:
热身:
寻找数组的中心下标
724. 寻找数组的中心下标 - 力扣(LeetCode)![]() https://leetcode.cn/problems/find-pivot-index/description/
https://leetcode.cn/problems/find-pivot-index/description/

题解:
运用前缀和就可以解决这个问题,注意在本题中,中心下标的左侧数之和、右侧数之和均不包括中心下标的数。
我们定义前缀和、后缀和数组,根据题目要求,对前缀和数组的最左端、后缀和数组的最右端初始化为0。
代码:
class Solution {
public:int pivotIndex(vector<int>& nums) {int n=nums.size();vector<int> f(n);//前缀和vector<int> g(n);//后缀和f[0]=g[n-1]=0;for(int i=1;i<n;i++){f[i]=f[i-1]+nums[i-1];}for(int i=n-2;i>=0;i--){g[i]=g[i+1]+nums[i+1];}for(int i=0;i<n;i++){if(f[i]==g[i])return i;}return -1;}
};进阶:
除自身之外数组的乘积
238. 除自身以外数组的乘积 - 力扣(LeetCode)![]() https://leetcode.cn/problems/product-of-array-except-self/description/
https://leetcode.cn/problems/product-of-array-except-self/description/

题解:
由于题目要求不用除法,所以我们不可以算出数组全部元素的乘积后再去除以 nums[ i ] 来得到答案。
在寻找数组的中心下标中,我们算出了 nums[ i ] 左侧和、右侧和,我们可以按照这个思路,算出 nums[ i ] 左侧乘积、右侧乘积,把左右两侧乘积相乘,就可以得到除自身之外数组的乘积。
代码:
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n=nums.size();vector<int> f(n);//左侧乘积vector<int> g(n);//右侧乘积vector<int> ret(n);//返回值f[0]=g[n-1]=1;for(int i=1;i<n;i++)f[i]=f[i-1]*nums[i-1];for(int i=n-2;i>=0;i--)g[i]=g[i+1]*nums[i+1];for(int i=0;i<n;i++){ret[i]=f[i]*g[i];}return ret;}
};和为K的子数组
560. 和为 K 的子数组 - 力扣(LeetCode)![]() https://leetcode.cn/problems/subarray-sum-equals-k/description/
https://leetcode.cn/problems/subarray-sum-equals-k/description/

题解:
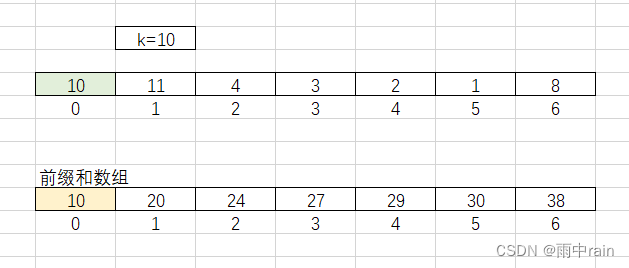
如下图,假设 k = 10,在给定的数组中,发现下标 2 ~ 5 的数组和 = k,而这一部分数组和,恰好为下标 0 ~ 5 的前缀和 - 下标 0 ~ 1 的前缀和(假设前缀和数组为 sum,则 K = sum[ 5 ] - sum[ 1 ] ),所以我们可以用前缀和数组,快速得到和为 K 的子数组。

为了获得和为 K 的子数组的个数,我们可以在计算前缀和的同时,用哈希表记录每一个前缀和出现的次数。
比如 K = sum[ 5 ] - sum[ 1 ] ,可以交换位置,变为 sum[ 5 ] - K = sum[ 1 ],由于记录了 sum[ 1 ] 出现的次数为 1 次,这样就可以得出当前和为 K 的子数组的个数为 1 个。
由于我们用哈希表记录了每一个前缀和出现的个数,所以前缀和的计算可以不采用数组。
可能会出现以下情况:前缀和 sum - k == 0,但是哈希表中记录的前缀和并不存在 0,怎么处理?
既然哈希表中不存在前缀和 0,那我们可以先放一个 0 进去,并把出现的次数设置为 1.
代码:
class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int,int> hash;int ret=0,sum=0;hash[0]=1;for(int i=0;i<nums.size();i++){sum+=nums[i];if(hash.count(sum-k)) {ret+=hash[sum-k];}hash[sum]++;}return ret;}
};和可被 K 整除的子数组
974. 和可被 K 整除的子数组 - 力扣(LeetCode)![]() https://leetcode.cn/problems/subarray-sums-divisible-by-k/description/
https://leetcode.cn/problems/subarray-sums-divisible-by-k/description/

题解:
同余定理:
假设 a % k == b % k ,则 ( a - b ) % k = 0.
举个例子,假设 k = 5,23 % 5 = 13 % 5,则(23 - 23 )% 5 = 0.
我们可以运用同余定理来解决这道题:
和上一题的思路相似,我们用 i 遍历数组,计算出下标 0 ~ i 的前缀和 sum,用哈希表记录 sum % K 出现的次数,如果 sum % K 曾经出现过,则存在和可被 K 整除的子数组,返回值 += 次数。
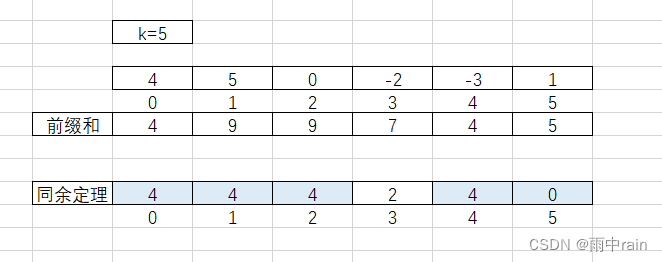
以示例 1 为例,假设返回值为 ret,比如下标 0 ~ 1 的前缀和取模后为 4,而下标 0 的前缀和取模后也为 4 ,而在此之前取模后为 4 出现的次数为 1,根据同余定理,子数组 [ 5 ] 可以被 K 整除,ret += 1,同理,下标 0 ~ 2 的前缀和取模后为 4,而在此之前取模后为 4 出现的次数为 2 ,所以此时 ret+=2 ,分别为 [ 5 ] , [ 5 , 0 ] , [ 0 ] ;下标 0 ~ 4 的前缀和取模后为 4,而在此之前取模后为 4 出现的次数为 3,所以此时 ret += 3 ,和可被 K 整除的子数组有 6 个,分别为 [ 5 ] , [ 5 , 0 ] , [ 0 ], [ 0, -2 , -3 ] , [ -2 , -3 ] ,[ 5 , 0, -2 , -3 ] ,以此类推。
注意 0 也可以被 K 整除!
为什么需要修正负数取模?
我们观察下面的例子:

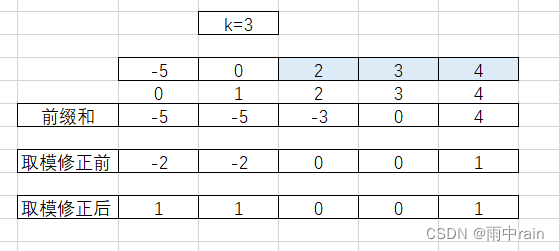
存在子数组 [ 2, 3, 4 ] 的和可以被 3 整除,但是这在前缀和中无法体现出来。
再举个例子:
1、 7 % 3 = 1 , ( -2 ) % 3 = -2 ,但 [ 7 - ( -2 ) ] % 3 = 0 ;
2、( - 2) % 3 = -2 , ( -5 ) % 3 = -2 ,[ -2 - ( -5 ) ] % 3 = 0 。
可以看出当 a、b 同正同负时, a % k == b % k ,可以推出 ( a - b ) % k = 0,可以推出和可被 K 整除的子数组,但 a、b一正一负时,就没办法推出。
为了让同余定理在一正一负的情况下也可以成立,我们可以对负数取模进行修正,把取模后的结果修改为正数,这样 a、b 就都是正数:
int r=(sum%k+k)%k;再回到一开始举的例子,通过修正取模后,就可以得到正确的结果:
代码:
class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {int sum=0,ret=0;unordered_map<int,int> hash;hash[0]=1;for(int i=0;i<nums.size();i++){sum+=nums[i];int r=(sum%k+k)%k;if(hash.count(r)) ret+=hash[r];hash[r]++;}return ret;}
};连续数组
525. 连续数组 - 力扣(LeetCode)

这道题用到的方法比较巧妙,利用了前缀和,
1、如果 nums[ i ] 为 0,则 sum += -1;
2、如果 nums[ i ] 为 1,则 sum += 1。
如果此时的前缀和 sum 在之前已经出现过了,假设上一次出现的下标为 j,说明 i 和 j 中间的这段数组的 0 和 1 的数量相等,只有相等了,才会相互抵消,前缀和才会再次变为 sum。
代码:
class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int,int> hash;hash[0]=-1;int ret=0;int sum=0;for(int i=0;i<nums.size();i++){sum+=(nums[i]==0?-1:1);if(hash.count(sum)) ret=max(ret,i-hash[sum]);else hash[sum]=i;}return ret;}
};相关文章:

前缀和(下)
目录 热身: 寻找数组的中心下标 题解: 代码: 进阶: 除自身之外数组的乘积 题解: 代码: 和为K的子数组 题解: 代码: 和可被 K 整除的子数组 题解: 同余定理…...

【排序算法】希尔排序
前言:学习希尔排序前最好先掌握插入排序,在进行;不会的可以点击——>【排序算法】插入排序-CSDN博客 一、希尔排序: 希尔排序,也称为缩小增量排序,是一种基于插入排序的快速改进算法。由Donald Shell于1…...
数学建模--LaTex插入表格详细介绍
目录 1.插入普通的边线表格 3.三线表的插入和空格说明 3.基于复杂情况下表格的插入 1.插入普通的边线表格 (1)像这个右边的生成的这个比较普通的表格,我们是使用下面的代码实现的: (2)和插入一个一个图片…...

未来已来:Flutter引领的安卓与跨平台开发奇幻之旅
引言 随着移动开发技术的飞速发展,跨平台开发框架如Flutter正逐渐改变着传统的安卓和iOS开发格局。作为一名资深的安卓开发工程师,我深刻感受到了Flutter带来的变革和机遇。今天,我想与大家分享Flutter在跨平台开发中的奇幻之旅,…...
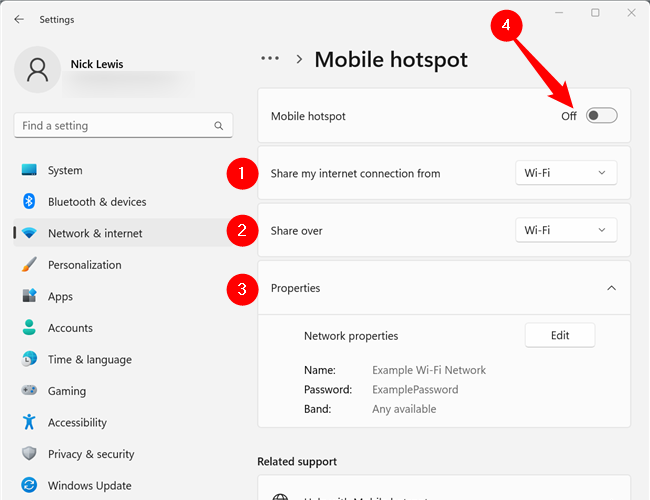
如何将Windows PC变成Wi-Fi热点?这里提供详细步骤
序言 Windows 10和Windows 11都有内置功能,可以将你的笔记本电脑(或台式机)变成无线热点,允许其他设备连接到它并共享你的互联网连接。以下是操作指南。 由于Windows中隐藏的虚拟Wi-Fi适配器功能,你甚至可以在连接到另一个Wi-Fi网络或无线路由器时创建Wi-Fi热点,通过另…...
“)
报错:Cannot invoke “springfox.documentation.service.ParameterType.getIn()“
文章目录 前言一、报错分析二、解决办法修改代码 总结 前言 遇到报错:Cannot invoke "springfox.documentation.service.ParameterType.getIn()" because the return value of "springfox.documentation.service.RequestParameter.getIn()" is …...
一个生动的例子——通过ERC20接口访问Tether合约
生动的例子 USDT:符合ERC20标准的美元稳定币,Tether合约获得测试网上Tether合约地址通过自己写的ERC20接口访问这个合约 Tether合约地址:0xdAC17F958D2ee523a2206206994597C13D831ec7 IERC20.sol // SPDX-License-Identifier: GPL-3.0pra…...

新媒体时代,LCD电子价签赋予零售场景新活力
近年来,全球企业迅速掀起了数字化转型的浪潮,加速了新零售科技的发展与应用。在实体零售门店中,商品货架显示逐渐趋向智能化和多样化。然而,在信息传播日益碎片化和视频化的时代,零售门店如何更有效地吸引消费者的注意…...
芋道源码 / yudao-cloud:前端技术架构探索与实践
摘要: 随着企业信息化建设的深入,后台管理系统在企业运营中扮演着至关重要的角色。本文将以芋道源码的yudao-cloud项目为例,深入探讨其前端技术架构的设计思路、关键技术与实现细节,并分享在开发过程中遇到的挑战与解决方案。 一、…...

2024 angstromCTF re 部分wp
Guess the Flag 附件拖入ida 比较简单,就一个异或 switcher 附件拖入ida 明文flag Polyomino 附件拖入ida 需要输入九个数,然后进入处理和判断,如果满足条件则进入输出flag部分,flag和输入有关,所以要理解需要满足什么…...
STL库--priority_queue
目录 priority_queue定义 prority_queue容器内元素的访问 priority_queue()常用函数实例解析 priority_queue内元素优先级的设置 priority_queue的常见用途 priority_queue又称为优先队列,其底层是用堆来进行实现的。在优先队列中,队首元素一定是当…...
网络编程 —— Http使用httpClient实现页面爬虫
先去找类型的a标签 取出图片所在网址 取出https://desk.3gbizhi.com/deskMV/438.html 搭建Form界面 Http类 public static HttpClient Client { get; } static Http() {HttpClientHandler handler new HttpClientHandler();//处理消息对象//ServerCertificateCustomValidat…...
【本地运行chatgpt-web】启动前端项目和service服务端项目,也是使用nodejs进行开发的。两个都运行成功才可以使用!
1,启动web界面 https://github.com/Chanzhaoyu/chatgpt-web#node https://nodejs.org/en/download/package-manager # 使用nvm 安装最新的 20 版本。 curl -o- https://raw.githubusercontent.com/nvm-sh/nvm/v0.39.7/install.sh | bash source /root/.bashrc n…...
知识点(一))
TOGAF企业架构章节(核心)知识点(一)
TOGAF标准9.2一共有 6 部分: 第一部分(简介):企业架构的关键概念,特别是 TOGAF 方法进行了概要介绍第二部分(架构开发方法): TOGAF 框架的核心部分。描述了 TOGAF 架构开发方法&…...
手摸手教你uniapp原生插件开发
行有余力,心无恐惧 这篇技术文章写了得有两三个礼拜,虽然最近各种事情,工作上的生活上的,但是感觉还是有很多时间被浪费.还记得几年前曾经有一段时间7点多起床运动,然后工作学习,看书提升认知.现在我都要佩服那会儿的自己.如果想回到那种状态,我觉得需要有三个重要的条件. 其…...

C++进程间通信 消息队列
C进程间通信 消息队列 消息队列概述消息队列代码示例1. 创建和发送消息的程序(sender.cpp)2. 接收消息的程序(receiver.cpp) 代码解释运行步骤运行结果 消息队列概述 消息队列是一种进程间通信机制,允许一个或多个进程…...
mysql中InnoDB的统计数据
大家好。我们知道,mysql中存在许多的统计数据,比如通过SHOW TABLE STATUS 可以看到关于表的统计数据,通过SHOW INDEX可以看到关于索引的统计数据,那么这些统计数据是怎么来的呢?它们是以什么方式收集的呢?今…...

P459 包装类Wrapper
包装类的分类 1)针对八种基本数据类型相应的引用类型——包装类。 2)有了类的特点,就可以调用类中的方法。 Boolean包装类 Character包装类 其余六种Number类型的包装类 包装类和基本数据类型的相互转换 public class Integer01 {publi…...
Kong网关的负载均衡
安装java环境 查询 java安装包 196 yum list java* 安装java8197 yum install -y java-1.8.0-openjdk.x86_64 检验java8是否安装成功。198 java -version2个tomcat准备 另外一个tomcat区别在于:配置文件。conf/server.xml 启动tomcat [rootlocalhost bin]# ./…...

这是一个逗号
还不太能是句号,随想录这两个月算是给我一个学算法的开头,感慨还是挺多的,但是语文功底很差,就接着写流水账吧。 高考前想报计算机,但是那年是先报志愿后考试,家里人劝我选择更稳一点的985,又说…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
