AVL树的模拟实现

我们上期提到了二叉搜索树，只是简单的讲了一下原理，那么今天我们就讲一下AVL树。

AVL树的概念

其实大家应该很奇怪，难道二叉搜索树不能存储数据吗？为什么要有AVL树呢？二叉搜索树有可能会有畸形的情况。像下图，数据比较分散的话，这棵树很正常，如果我们插入的数相对有序就会变成右边那样畸形的树。

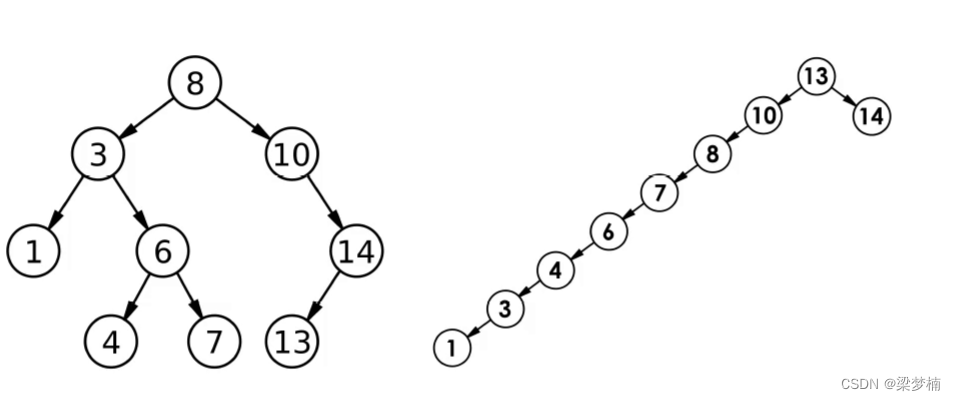
这个时候就需要人工干预，这里的AVL数就可以更好的控制这个情况，它有自己的平衡规则：左右子树高度之差(平衡因子)绝对不超过1(-1,0,1)。如果不满足这个规则，那么我们就旋转。

AVL树的实现

因为AVL树也是二叉搜索树的一种，所以他也要满足二叉搜索树的条件，然后在满足他自己的平衡规则。

AVL树的架构

其实数的节点架构和整体架构并没有变，只是多了一个bf(平衡因子)，用来调节平衡。

struct AVLTreeNode
{AVLTreeNode(const pair<K, V> kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}AVLTreeNode* _left;AVLTreeNode* _right;AVLTreeNode* _parent;pair<K, V> _kv;int _bf;
};
template<class K,class V>
class AVLTree
{public:typedef AVLTreeNode<K,V> Node;private:Node* _root=nullptr;
}

insert插入

引用pair对象

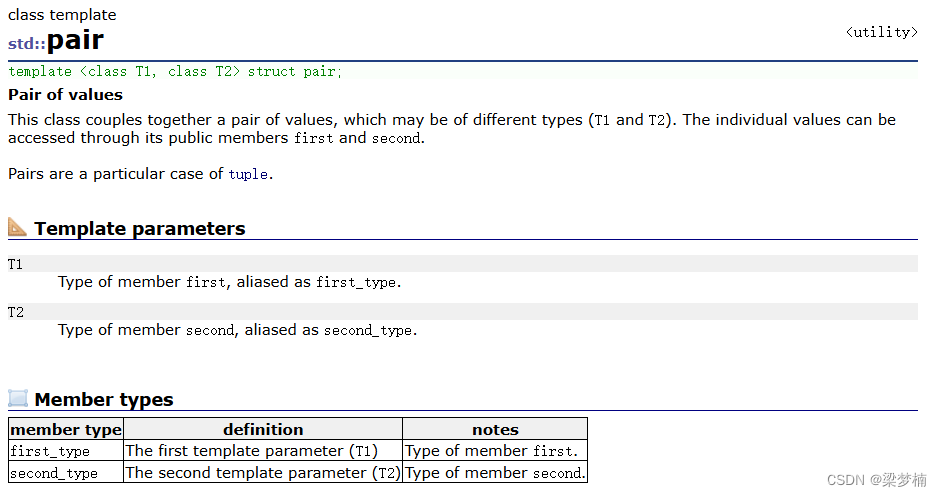
这里与原来不同，这里我们引入了一个pair对象，那么pair是什么？我们用pair来实现KV结构，在库中的map也是用pair也完成KV结构的，所以这里我们就用这pair。pair对象的first是K值，second是V值。

引进parent指针

这里引用父指针是因为我们将来要旋转，要不断向上调节平衡因子，因为当我们插入某个值有可能引起平衡因子失衡。

仅插入数据

其实插入部分和我们之前写的一样，只不过要注意的是，我们的值存的是pair对象，要像拿到K值需要 _kv.first拿到K值。一定要遵循二叉搜索树的规律，左子树比根小，右子树比根大。

	if (_root == nullptr){//插入第一个值Node* newNode = new Node(kv);_root = newNode;return true;}Node* newNode = new Node(kv);Node* cur = _root;Node* parent = cur;while (cur){if (cur->_kv.first < newNode->_kv.first){//大于在右边parent = cur;cur = cur->_right;}else if (cur->_kv.first > newNode->_kv.first){//小于在左边parent = cur;cur = cur->_left;}else{//等于,二叉搜索树不允许冗余，所以直接返回false。return false;}}if (parent->_kv.first > newNode->_kv.first){//在左边parent->_left = newNode;}else{//在右边parent->_right = newNode;}newNode->_parent = parent;

调节平衡因子

情况1：插入在父亲的右边，父亲的平衡因子++后为0

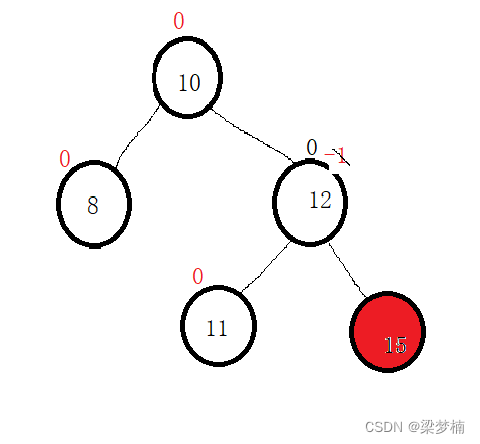
红色是我插入的数，插入后，它的parent：12从-1加加后变成了0，我们还需要向上更新吗？答案是不需要向上更新，为什么？0表示左右子树的高度差为0，也就说高度没有变，所以我不需要再向上更新。
解释：平衡因子原来是1/-1都表示这个树缺了一个节点，当我们插入之后正好填上了这个节点，但是高度并不变。看图！我把15插入，右子树这个高度没有变。

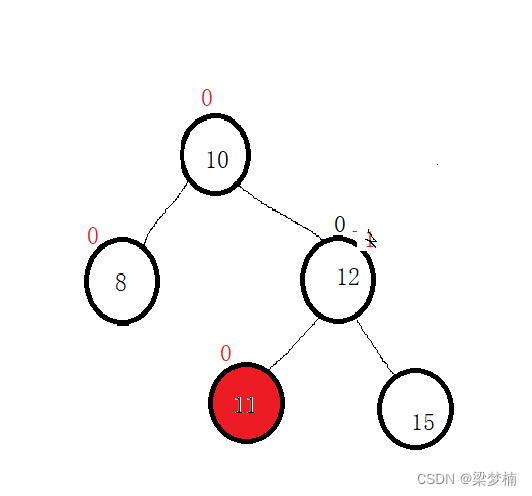
情况2：插入在父亲的左边，父亲的平衡因子–后为0

当我插入在左边，那我们就需要给父亲的因子bf–。

情况3：插入左或者右，恰巧父亲不是0，是-1/1

父亲的平衡因子==1/-1，父亲所在子树高度变了。高度变了继续向上更新。

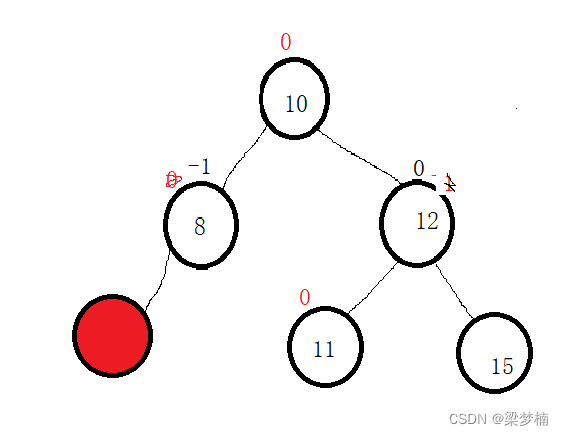
情况4：当父亲的平衡因子==-2/2，不需要在更新了，证明不平衡了，需要旋转。

这个时候就不满足AVL树的规则了，就需要旋转。

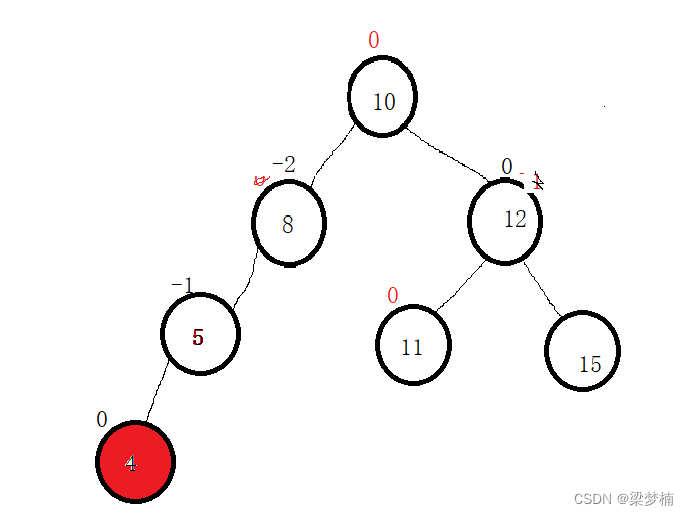
左边高，右旋

这个树就是左边高的情况，你会发现parent为-2，cur为-1，这个情况就是左边比右边要高，那么我们需要右旋。

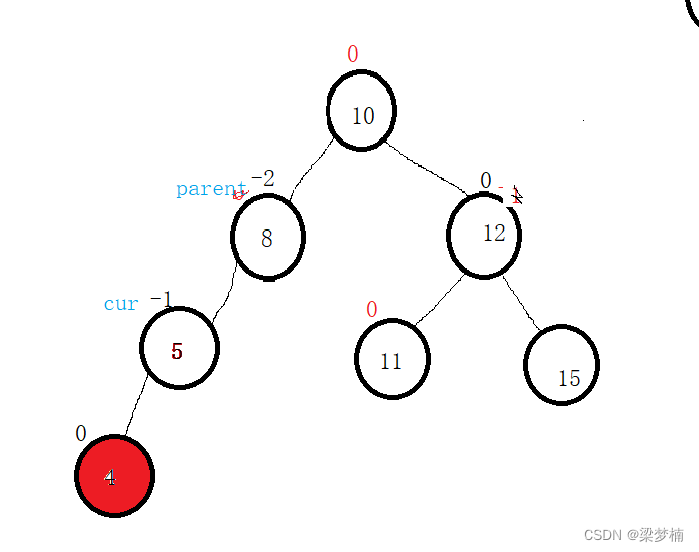
右旋的口诀：把cur的右边给parent的左边，cur的右边链接parent，在让parent的parent链接cur。会发现我们把原来的parent变成了cur的右边。并且现在是平衡的。

其实为什么要把cur的右边给parent呢？是因为cur的右边时当前树最大的值，cur给了parent链接到左边，依然不会破坏二叉搜索树的规则。

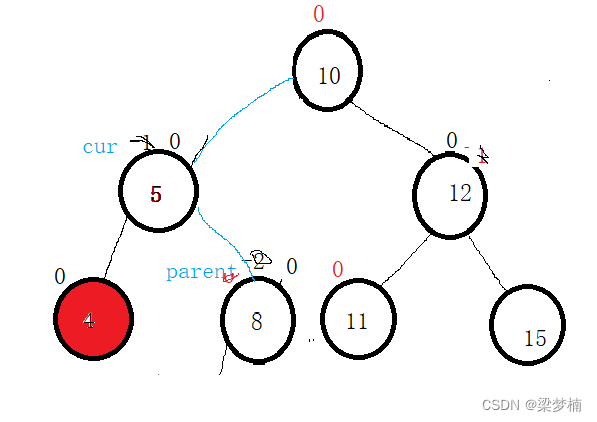
void RotateR(Node* parent )
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppNode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}parent->_bf = subL->_bf = 0;
}

右边高，左旋

当我们插入红色节点的时候就会导致右边过高，那么我们就需要左旋。

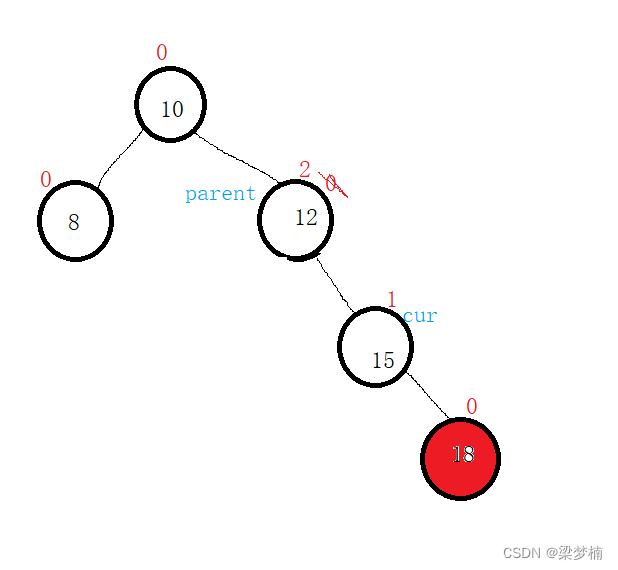
左旋的口诀：让cur的左边给parent的右边链接，然后让父亲变成cur的左边。
解释：为什么要把cur左边的值给parent的右边？cur当前位置是parent的右边，cur的左边也是比parent大的值，给parent的右边依然不影响二叉搜索树的规则。

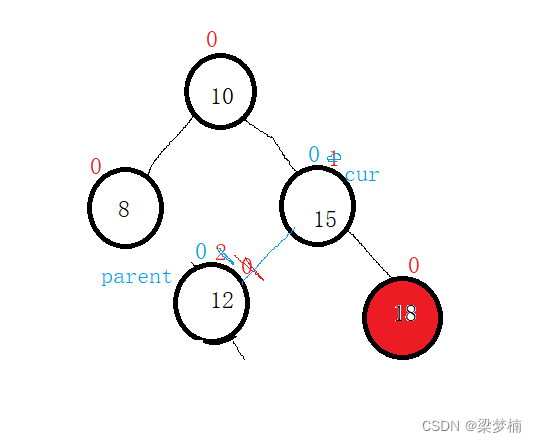
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if(subRL)subRL->_parent = parent;subR->_left = parent;Node* pphead = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (pphead->_parent == parent){pphead->_right = subR;}else{pphead->_left = subR;}subR->_parent = pphead;}subR->_bf = parent->_bf = 0;
}

双旋转

还有一种情况，它并不是单纯的一边高，用单旋并不能解决问题。当我们仅仅只是单旋会发现他有变成了形态不同，但是问题一样的情况，这个时候就需要双旋。

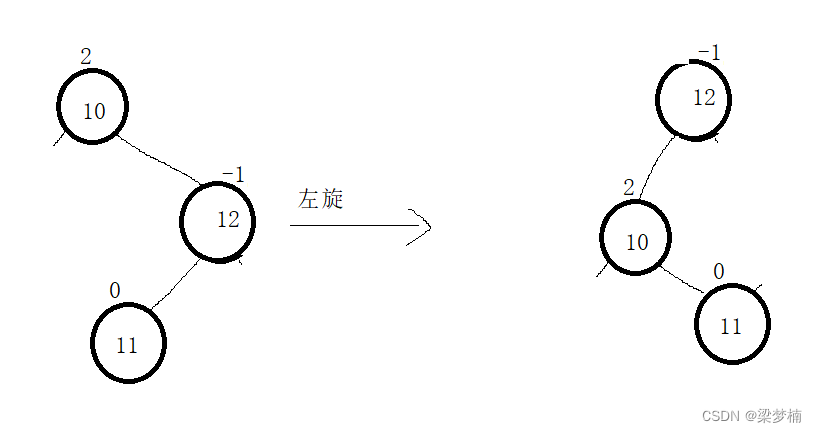
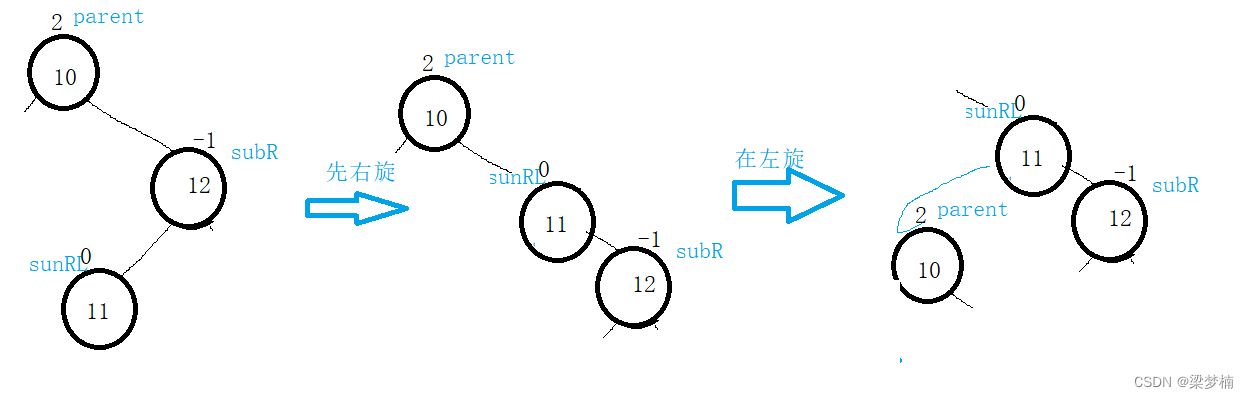
右左旋转：先右旋然后左旋。

既然我们单旋解决不了问题，我们可以把他变成一边高，然后进行单旋。
如这个图，我们可以对subR进行右旋后，在对parent左旋就可以了。

右左双旋后：

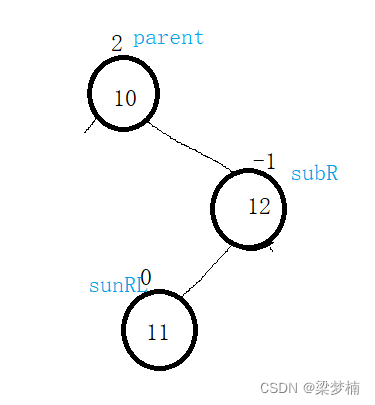
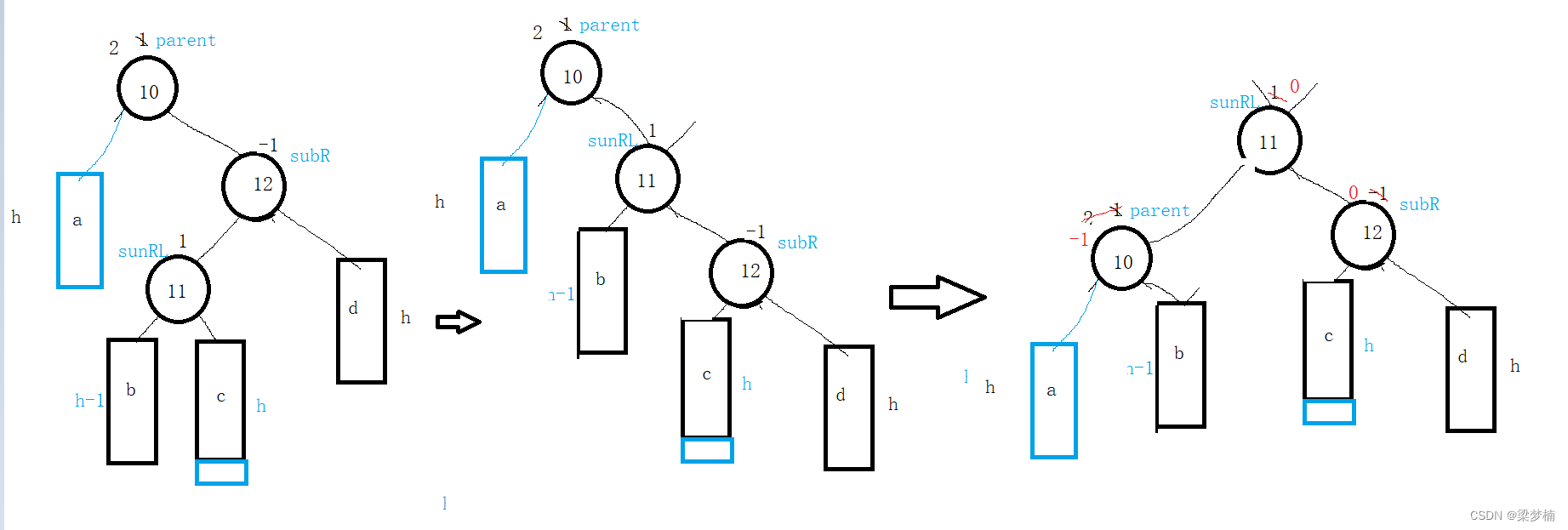
但是有个问题，平衡因子我们应该如何更新？你可能会说这种情况不是正好满足左旋/右旋后平衡因子变成0吗？但是如果其他位置都有节点呢？接下来我们抽象图，给大家演示一下。
当我们插入节点的位置不同，你会发现每一个平衡因子也不一样。如图：我插在了右边。这个时候我通过右左双旋就会得到下图。如最右图的红色平衡因子，应该变成这个情况。所以说插入的位置不同，平衡因子也会不同。

如图：假如我插在了左边。会发现平衡因子又不一样了。所以我们并不能用一个例子来概括所有。

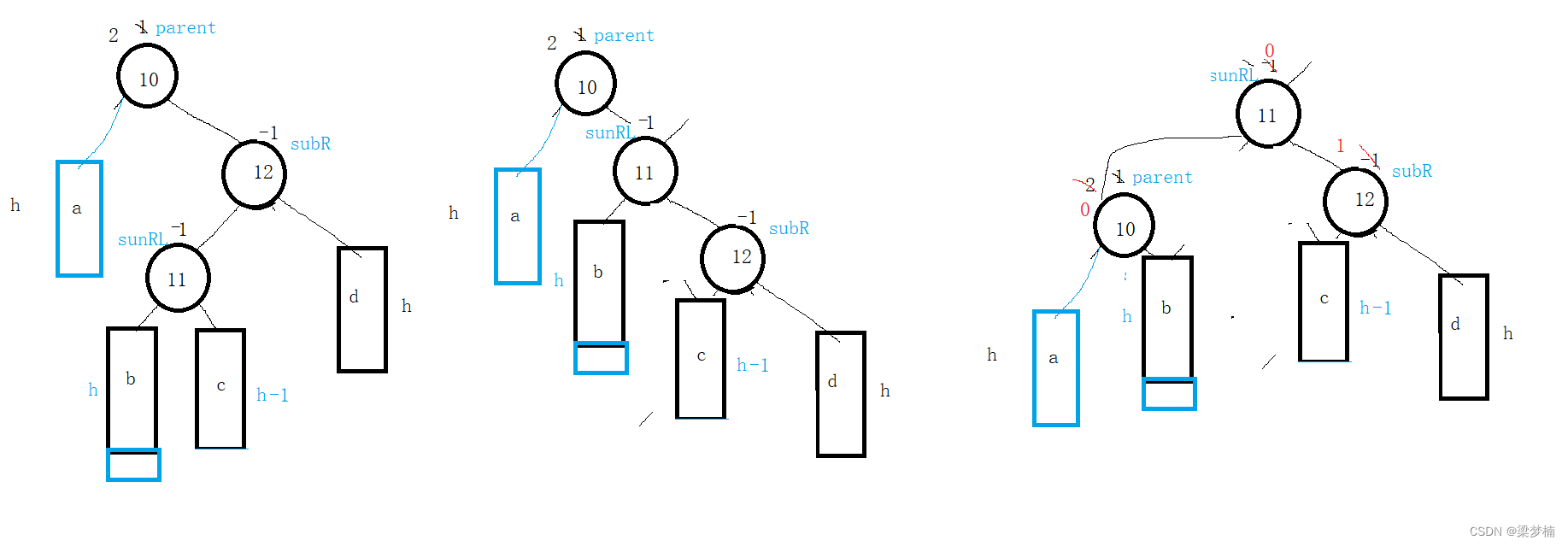
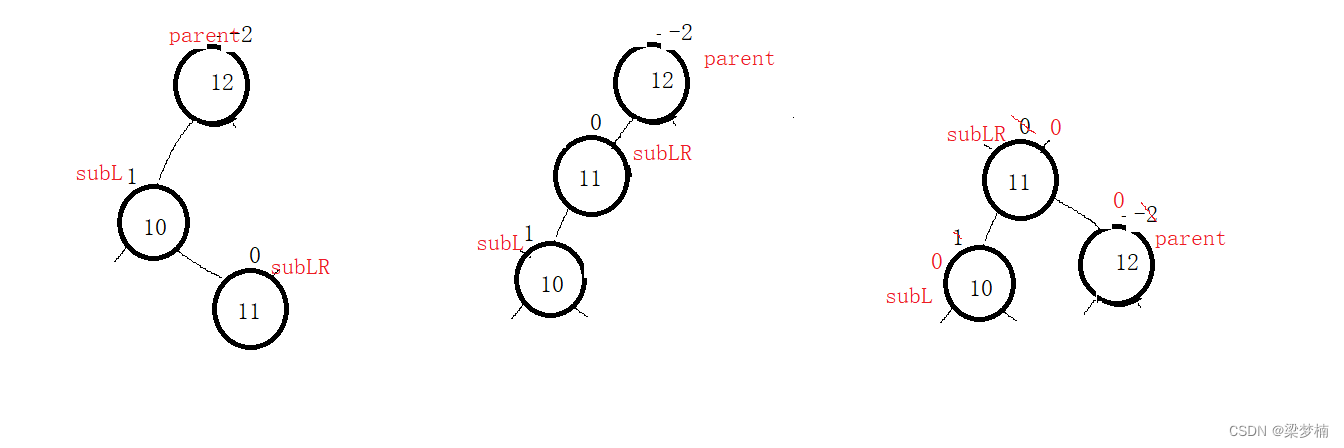
那么我们应该怎么做呢？其实从我们画图，你会发现我们改变的只不过是parent 、subR、sunRL这三个节点的因子，其他的并没有改变。并且，跟subRL的因子有密切关系，所以我们只需要判断subRL的因子是0/1/-1就能修改他们三个因子。

		void RotateRL(Node* parent){//右左双旋//平衡因子需要自己调节Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 0){//新插入的parent->_bf =0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 1){//右边插入的subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if(bf==-1){//在左边插入的parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else{assert(false);}}

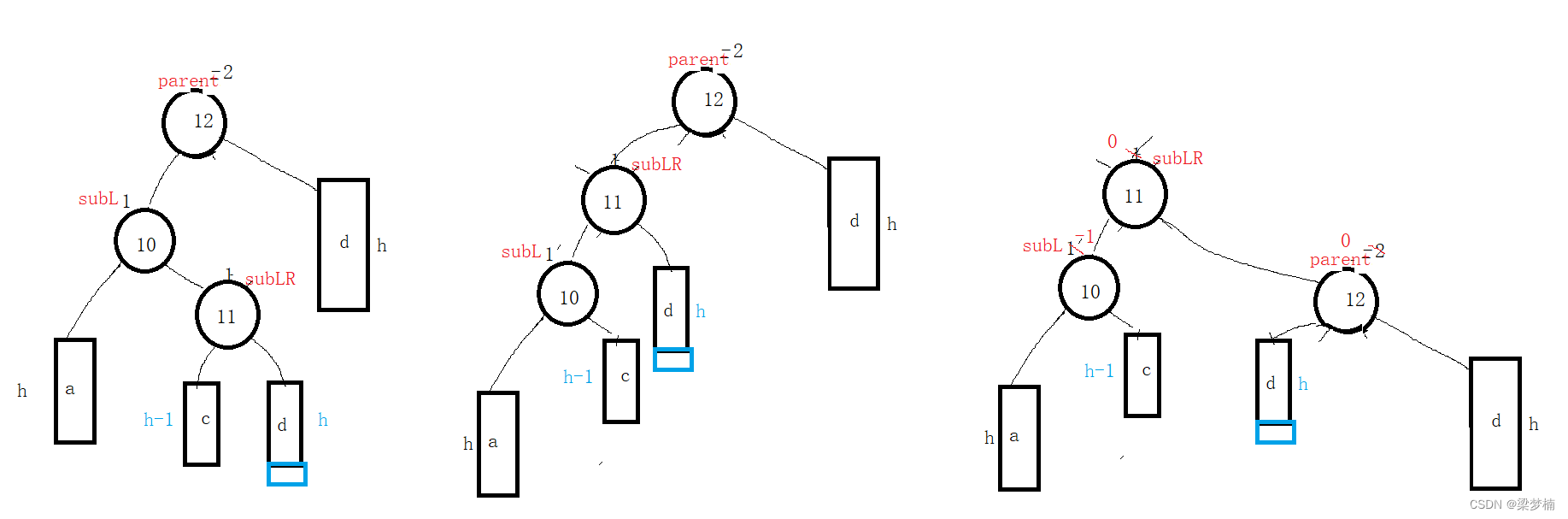
左右双旋：先左旋，在右旋。

图下是：左右双旋。

当然了，我们依然需要分析平衡因子，所以我们依然要分析插入在哪个位置。
如图：当插入在右边。

如图：当我们插在左边。

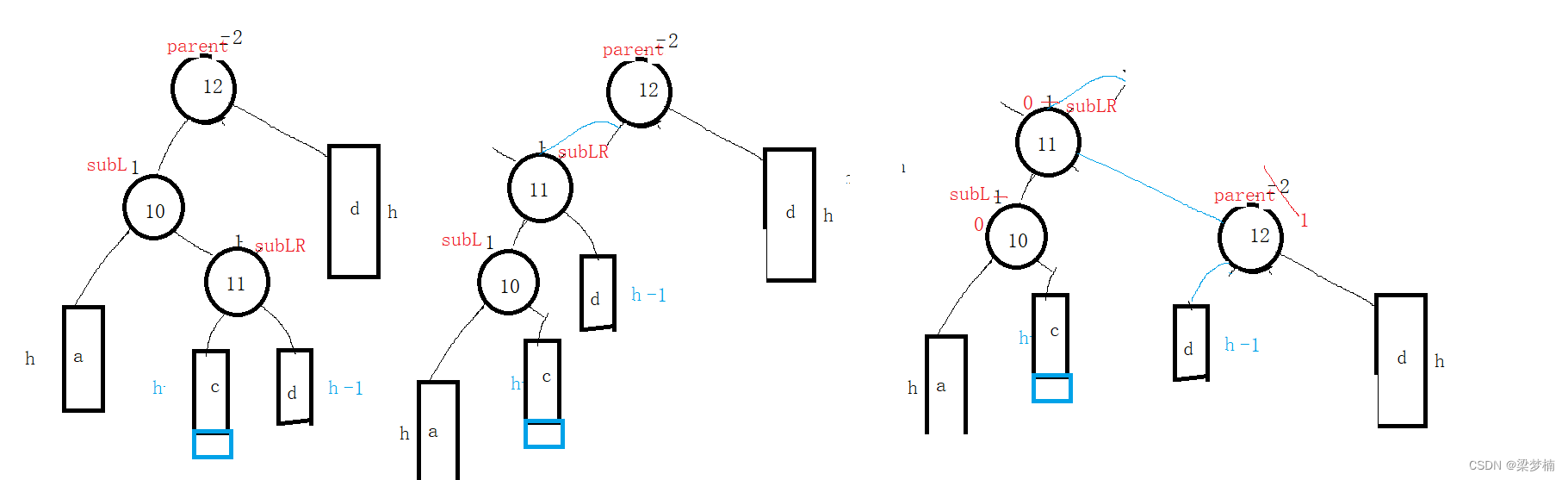
		void RotateLR(Node* parent){//左右双旋//平衡因子需要单独调节Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;//先左旋在右旋RotateL(parent->_left);RotateR(parent);//重新计算调节因子if (bf == 0){//当且节点就是新插的subL->_bf = 0;parent->_bf = 0;subLR->_bf = 0;}else if(bf==1){//在当前节点的右边插入的parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if(bf == -1){subL->_bf = 0;parent->_bf = 1;subLR->_bf = 0;}else{assert(false);}}

中序遍历

因为二叉搜索树我们都是中序遍历，因为中序遍历更接近有序。

void _Inorder(Node* root)
{if (root == nullptr){return;}_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second<<endl;_Inorder(root->_right);
}

判断是否平衡

什么时候不平衡？是不是因子大于等于2的时候，所以我们需要算左右树的高度相减，如果超过2，那就是不平衡。

		bool _isBalance(Node* root){if (root == nullptr){return true;}int left = _Height(root->_left);int right = _Height(root->_right);if (abs(left - right) >= 2) return false;//因子大于等于2的时候不平衡return _isBalance(root->_left) && _isBalance(root->_right);}int _Height(Node* root){if (root == nullptr)return 0;int left = _Height(root->_left);int right = _Height(root->_right);return max(left, right) + 1;}

AVL树整体代码

以下是整个AVL树所有的代码？

问题：为什么没有像库一样写删除呢？答：我们模拟实现其实是为了了解底层，并不是要超过底层，因为现有的库已经很好了，我们没必要写一个。二叉搜索树很少用删除接口。所以这里没有实现。

#pragma once
#include<iostream>
#include<vector>
#include<string>
#include<assert.h>using namespace std;
namespace KV
{template<class K,class V>struct AVLTreeNode{AVLTreeNode(const pair<K, V> kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}AVLTreeNode* _left;AVLTreeNode* _right;AVLTreeNode* _parent;pair<K, V> _kv;int _bf;};template<class K,class V>class AVLTree{public:typedef AVLTreeNode<K,V> Node;bool insert(const pair<K, V> kv){if (_root == nullptr){//插入第一个值Node* newNode = new Node(kv);_root = newNode;return true;}Node* newNode = new Node(kv);Node* cur = _root;Node* parent = cur;while (cur){if (cur->_kv.first < newNode->_kv.first){//大于在右边parent = cur;cur = cur->_right;}else if (cur->_kv.first > newNode->_kv.first){//小于在左边parent = cur;cur = cur->_left;}else{//等于,二叉搜索树不允许冗余，所以直接返回false。return false;}}if (parent->_kv.first > newNode->_kv.first){//在左边parent->_left = newNode;}else{//在右边parent->_right = newNode;}newNode->_parent = parent;cur = newNode;while (parent){if (parent->_left == cur){cur->_parent->_bf--;}else if (parent->_right == cur){cur->_parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//出现健康问题需要旋转//左边高，右旋转if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//右边高，左旋转else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){//左右双旋RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){//右左双旋RotateRL(parent);}else{assert(false);}}else{//按道理说不可能有这种情况，但是保不准会有bugassert(false);break;}}return true;}void Inorder(){_Inorder(_root);}int Height(){return _Height(_root);}bool isBalance(){return _isBalance(_root);}private:int _Height(Node* root){if (root == nullptr)return 0;int left = _Height(root->_left);int right = _Height(root->_right);return max(left, right) + 1;}bool _isBalance(Node* root){if (root == nullptr){return true;}int left = _Height(root->_left);int right = _Height(root->_right);if (abs(left - right) >= 2) return false;return _isBalance(root->_left) && _isBalance(root->_right);}void RotateRL(Node* parent){//右左双旋//平衡因子需要自己调节Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 0){//新插入的parent->_bf =0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 1){//右边插入的subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if(bf==-1){//在左边插入的parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else{assert(false);}}void RotateLR(Node* parent){//左右双旋//平衡因子需要单独调节Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;//先左旋在右旋RotateL(parent->_left);RotateR(parent);//重新计算调节因子if (bf == 0){//当且节点就是新插的subL->_bf = 0;parent->_bf = 0;subLR->_bf = 0;}else if(bf==1){//在当前节点的右边插入的parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if(bf == -1){subL->_bf = 0;parent->_bf = 1;subLR->_bf = 0;}else{assert(false);}}void RotateR(Node* parent ){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppNode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}parent->_bf = subL->_bf = 0;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if(subRL)subRL->_parent = parent;subR->_left = parent;Node* pphead = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (pphead->_parent == parent){pphead->_right = subR;}else{pphead->_left = subR;}subR->_parent = pphead;}subR->_bf = parent->_bf = 0;}void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second<<" 因子：" <<root->_bf<< endl;_Inorder(root->_right);}Node* _root=nullptr;};
}