模拟集成电路(5)----单级放大器(共栅级)
模拟集成电路(5)----单级放大器(共栅级)
有一些场合需要一些小的输入电阻(电流放大器)

大信号分析
− W h e n V i n ≥ V B − V T H ∙ M 1 i s o f f , V o u t = V D D − F o r L o w e r V i n I d = 1 2 μ n C o x W L ( V B − V i n − V T H ) 2 V o u t = V D D − 1 2 μ n C o x W L ( V B − V i n − V T H ) 2 ⋅ R D \begin{aligned} &-\mathrm{~When~}V_{in}\geq V_B-V_{TH} \\ &\bullet\mathrm{M}_1\mathrm{~is~off},V_{out}=V_{DD} \\ &-\mathrm{~For~Lower~}V_{in} \\ &I_{d}=\frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}(V_{B}-V_{in}-V_{TH})^{2} \\ &V_{out}=V_{DD}-\frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}(V_{B}-V_{in}-V_{TH})^{2}\cdot R_{D} \end{aligned} − When Vin≥VB−VTH∙M1 is off,Vout=VDD− For Lower VinId=21μnCoxLW(VB−Vin−VTH)2Vout=VDD−21μnCoxLW(VB−Vin−VTH)2⋅RD
− When V i n < V i n 1 , M 1 enters triode region V D D − 1 2 μ n C o x W L ( V B − V i n 1 − V T H ) 2 ⋅ R D = V B − V T H \begin{aligned}&-\text{ When }V_{in}<V_{in1},\text{M}_1\text{ enters triode region}\\&V_{DD}-\frac12\mu_nC_{ox}\frac{W}L(V_B-V_{in1}-V_{TH})^2\cdot R_D=V_B-V_{TH}\end{aligned} − When Vin<Vin1,M1 enters triode regionVDD−21μnCoxLW(VB−Vin1−VTH)2⋅RD=VB−VTH
大信号特性图

求增益
V o u t = V D D − 1 2 μ n C o x W L ( V B − V i n − V T H ) 2 R D ∂ V o u t ∂ V i n = − μ n C o x W L ( V B − V i n − V T H ) ( − 1 − ∂ V T H ∂ V i n ) R D \begin{aligned}&V_{out}=V_{DD}-\frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}(V_{B}-V_{in}-V_{TH})^{2}R_{D}\\&\frac{\partial V_{out}}{\partial V_{in}}=-\mu_{n}C_{ox}\frac{W}{L}(V_{B}-V_{in}-V_{TH})(-1-\frac{\partial V_{TH}}{\partial V_{in}})R_{D}\end{aligned} Vout=VDD−21μnCoxLW(VB−Vin−VTH)2RD∂Vin∂Vout=−μnCoxLW(VB−Vin−VTH)(−1−∂Vin∂VTH)RD
∵ ∂ V T H / ∂ V i n = ∂ V T H / ∂ V S B = η , A ν = ∂ V o u t ∂ V i n = μ n C o x W L ( V B − V i n − V T H ) ( 1 + η ) R D \because\quad\partial V_{TH}/\partial V_{in}=\partial V_{TH}/\partial V_{SB}=\eta,\\A_{\nu}=\frac{\partial V_{out}}{\partial V_{in}}=\mu_{n}C_{ox}\frac{W}{L}(V_{B}-V_{in}-V_{TH})(1+\eta)R_{D} ∵∂VTH/∂Vin=∂VTH/∂VSB=η,Aν=∂Vin∂Vout=μnCoxLW(VB−Vin−VTH)(1+η)RD
A ν = g m ( 1 + η ) R D A_\nu=g_m(1+\eta)R_D Aν=gm(1+η)RD
小信号分析

ν b s = − ν i n ν 1 = − ν i n \nu_{bs}=-\nu_{in}\quad\nu_{1}=-\nu_{in} νbs=−νinν1=−νin
ν o u t = − [ g m ν 1 + g m b ν b s + ( ν o u t − ν i n ) / r o ] ⋅ R D \nu_{out}=-[g_{m}\nu_{1}+g_{mb}\nu_{bs}+(\nu_{out}-\nu_{in})/r_{o}]\cdot R_{D} νout=−[gmν1+gmbνbs+(νout−νin)/ro]⋅RD
A ν = ν o u t ν i n = g m + g m b + 1 / r o 1 + R D / r o ⋅ R D ≈ ( g m + g m b ) ⋅ R D A_{\nu}=\frac{\nu_{out}}{\nu_{in}}=\frac{g_{m}+g_{mb}+1/r_{o}}{1+R_{D}/r_{o}}\cdot R_{D}\approx(g_{m}+g_{mb})\cdot R_{D} Aν=νinνout=1+RD/rogm+gmb+1/ro⋅RD≈(gm+gmb)⋅RD
如果输入电流源有无限的阻抗 R s R_s Rs
ν 1 = − [ ν i n − ( ν o u t / R D ) ⋅ R S ) ν b s = ν 1 \nu_1=-[\nu_{in}-(\nu_{out}/R_D)\cdot R_S)\quad\nu_{bs}=\nu_1 ν1=−[νin−(νout/RD)⋅RS)νbs=ν1
ν o u t = − [ g m ν 1 + ( ν o u t + ν 1 ) / r o + g m b ν b s ] ⋅ R D A ν = ν o u t ν i n = g m + g m b + 1 / r o 1 + ( g m + g m b ) R S + ( R D + R S ) / r o ⋅ R D \nu_{out}=-[g_{m}\nu_{1}+(\nu_{out}+\nu_{1})/r_{o}+g_{mb}\nu_{bs}]\cdot R_{D}\\A_{\nu}=\frac{\nu_{out}}{\nu_{in}}=\frac{g_{m}+g_{mb}+1/r_{o}}{1+(g_{m}+g_{mb})R_{S}+(R_{D}+R_{S})/r_{o}}\cdot R_{D} νout=−[gmν1+(νout+ν1)/ro+gmbνbs]⋅RDAν=νinνout=1+(gm+gmb)RS+(RD+RS)/rogm+gmb+1/ro⋅RD
CG的输入电阻
ν 1 = − ν x ν b s = − ν x \nu_1=-\nu_x\quad\nu_{bs}=-\nu_x ν1=−νxνbs=−νx
i x R D + r o ( i x − ( g m + g m b ) ν x = ν x i_{x}R_{D}+r_{o}(i_{x}-(g_{m}+g_{mb})\nu_{x}=\nu_{x} ixRD+ro(ix−(gm+gmb)νx=νx
r i n = ν x i x = R D / r o + 1 1 / r o + ( g m + g m b ) ≈ 1 g m + g m b r_{in}=\frac{\nu_{x}}{i_{x}}=\frac{R_{D}/r_{o}+1}{1/r_{o}+(g_{m}+g_{mb})}\approx\frac{1}{g_{m}+g_{mb}} rin=ixνx=1/ro+(gm+gmb)RD/ro+1≈gm+gmb1
R D R_D RD的影响
r i n = ν x i x = R D / r o + 1 1 / r o + ( g m + g m b ) r_{in}=\frac{\nu_{x}}{i_{x}}=\frac{R_{D}/r_{o}+1}{1/r_{o}+(g_{m}+g_{mb})} rin=ixνx=1/ro+(gm+gmb)RD/ro+1
输出电阻
 $$ \begin{aligned}r_{out}&=r_{OD}\left\|R_{D}\right\|\\&=\{r_{O}+[1+(g_{m}+g_{mb})r_{O}]\cdot R_{S}\}\|R_{D}\end{aligned} $$
$$ \begin{aligned}r_{out}&=r_{OD}\left\|R_{D}\right\|\\&=\{r_{O}+[1+(g_{m}+g_{mb})r_{O}]\cdot R_{S}\}\|R_{D}\end{aligned} $$
− i f R s = 0 ⟶ r o u t = r O ∥ R D ∥ \begin{array}{cc}{-\mathrm{if}R_{s}=0}\\\\{\longrightarrow}&{r_{out}=r_{O}\left\|R_{D}\right\|}\\\end{array} −ifRs=0⟶rout=rO∥RD∥
相关文章:

模拟集成电路(5)----单级放大器(共栅级)
模拟集成电路(5)----单级放大器(共栅级) 有一些场合需要一些小的输入电阻(电流放大器) 大信号分析 − W h e n V i n ≥ V B − V T H ∙ M 1 i s o f f , V o u t V D D − F o r L o w e r V i n I d 1 2 μ n C o x W L ( V…...

学习笔记——数据通信基础——数据通信网络(网络工程师)
网络工程师 网络工程,就是围绕着网络进行的一系列的活动,包括∶网络规划、设计、实施、调试、排错等。网络工程设计的知识领域很宽广,其中路由和交换是计算机网络的基本。 网络工程师∶是在网络工程领域,掌握专业的网络技术&…...
将本地项目上传到 gitee 仓库
1、创建 gitee 仓库 到 gitee 官网,新建仓库 配置新建仓库 完成仓库的创建 项目上传到仓库 上传项目需要安装git git官方下载地址:git下载地址 安装完成,前往本地项目所在文件夹,右击选择 Git Bash Here 刚下载完成需要配置G…...

Django学习
1.pycharm社区版创建django PyCharm社区版如何创建Django项目并运行_pycharm社区版打开django-CSDN博客 2.Django TemplateDoesNotExist: rest_framework 当我们使用djangorestframework框架时,首先下载pip install djangorestframework 参考博文Django Templat…...

说唱程序员
Yo yo yo,这里是代码的战场,程序员的秀场, 键盘敲击声,是我们的节奏响亮。 夜深人静时,我们与Bug正面刚, 调试、优化,每一行代码都得刚强。 我们不懂数理化,只是喜欢瞎搞哈…...
058.最后一个单词的长度
题意 给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。 单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。 难度 简单 示例 1: 输入:s "Hello World" 输…...
决策树模型-预测用户是否购买某母婴产品
1,场景描述 假设我们是京东的数据分析师,负责分析母婴产品的购买行为。我们想预测用户是否会购买一款新上线的母婴产品。为了进行预测,我们将利用用户的历史购买数据、浏览行为和其他特征,通过决策树模型进行分析,并提…...

工具使用-网络性能测试工具(iperf)-TCP 和 UDP 的吞吐量-包转发率参数的理解
时间戳:2024年5月26日15:18:39 iperf 和 netperf 都是最常用的网络性能测试工具,测试 TCP 和 UDP 的吞吐量。它们都以客户端和服务器通信的方式,测试一段时间内的平均吞吐量。 接下来,我们就以 iperf 为例,看一下 TC…...

什么是JS引擎
JS引擎(JavaScript引擎)是负责在浏览器或Node.js等环境中解析和执行JavaScript代码的软件组件。它是JavaScript运行时的核心,将JavaScript代码转换为机器语言,使其能够在计算机上执行。 不同的浏览器和运行环境使用不同的JS引擎。…...

前端手写文件上传;使用input实现文件拖动上传
使用input实现文件拖动上传 vue2代码: <template><div><div class"drop-area" dragenter"highlight" dragover"highlight" dragleave"unhighlight" drop"handleDrop"click"handleClick&quo…...

Flutter 中的 PhysicalModel 小部件:全面指南
Flutter 中的 PhysicalModel 小部件:全面指南 Flutter 的 PhysicalModel 小部件提供了一种简单而高效的方式来给应用添加物理效果,如阴影和层次感。它本质上是一个矩形的 Container,带有圆角边框和可选的阴影,能够模仿真实世界中…...

Flutter 中的 Center 小部件:全面指南
Flutter 中的 Center 小部件:全面指南 在Flutter的世界里,Center是一个简单而强大的布局小部件,它能够将子组件放置在父组件的中心位置。无论是水平中心、垂直中心,还是两者都居中,Center都能轻松实现。本文将详细介绍…...
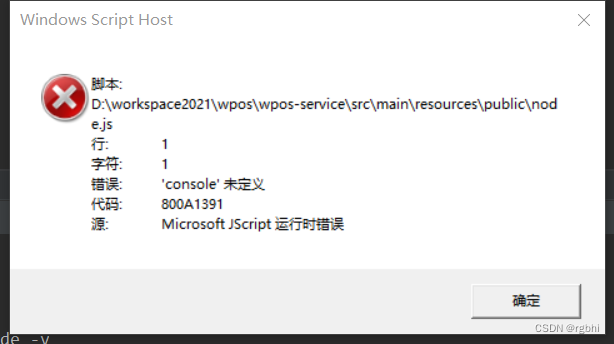
windows 执行node报错 800A1391
在项目下执行node -v的时候,抛了这个错误,一开始没发现有啥问题 现在一看,这个报错里的node怎么是个文件... 出现这个问题,是因为项目下,有个同名的文件叫node.js,搞得windows一时不知道是想打开node.js文…...

无人机操作界面来了,起点就很高呀。
无人机操作界面设计需要考虑以下几个方面: 易用性:无人机操作界面应该简单直观,易于操作和理解。操作按钮和控键应该布局合理,易于触摸或点击。重要的操作功能应该易于找到和使用,避免用户迷失或困惑。实时反馈&#…...

Android 11 AudioPolicyService 启动流程
AudioPolicyService在init进程中启动,源码路径:frameworks/av/media/audioserver/audioserver.rc service audioserver /system/bin/audioserverclass coreuser audioserver# media gid needed for /dev/fm (radio) and for /data/misc/media (tee)grou…...

java中static关键字面试五连问
抽象(abstract)方法是否可同时是静态的(static)? 抽象方法本来将来就是要被重写的,而静态方法不能被重写,所以是错误的 是否可以从一个静态(static)方法内部发出对非静态方法的调…...
基于文本来推荐相似酒店
基于文本来推荐相似酒店 查看数据集基本信息 import pandas as pd import numpy as np from nltk.corpus import stopwords from sklearn.metrics.pairwise import linear_kernel from sklearn.feature_extraction.text import CountVectorizer from sklearn.feature_extrac…...

红队内网攻防渗透:内网渗透之前置知识外网权限提升技术
红队内网攻防渗透 1. 内网权限提升技术1.1 外网权限提升的思路-前置知识1.1.1 外网权限提升知识点:1.1.2 外网权限提升基础内容1.1.2.1 为什么我们要学习权限提升转移技术:1.1.2.2 具体有哪些权限需要我们了解掌握的:1.1.2.3 以上常见权限获取方法简要归类说明:1.1.2.4 以上…...

【漏洞复现】大华智能物联综合管理平台 log4j远程代码执行漏洞
0x01 产品简介 大华ICC智能物联综合管理平台对技术组件进行模块化和松耦合,将解决方案分层分级,提高面向智慧物联的数据接入与生态合作能力。 0x02 漏洞概述 大华ICC智能物联综合管理平台/evo-apigw/evo-brm/1.2.0/user/is-exist 接口处存在 l0g4i远程…...
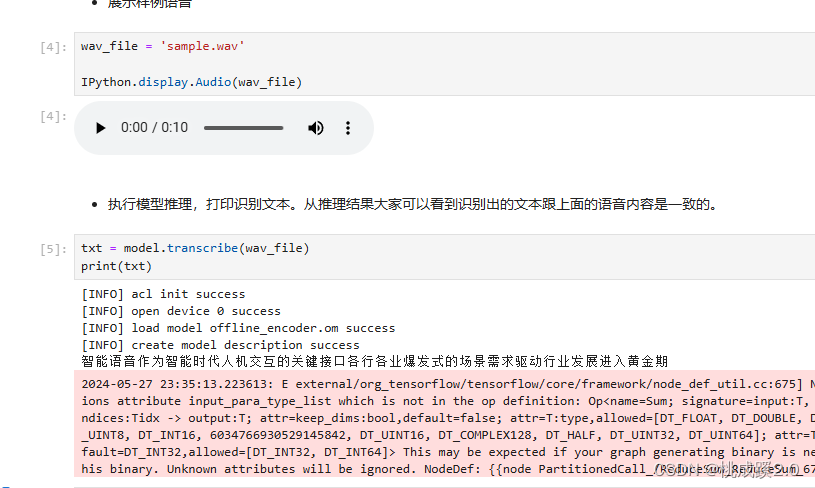
OrangePi AIpro测评
文章目录 1、外观部分2、系统初探3、AI性能体验4、总结 首先非常感谢csdn以及香橙派能够提供这样一个平台,可以测试OrangePi AIpro这样一块开发板,这块板子给我的感觉还是非常不错的,非常适合用来作为嵌入式学习的板子,性能也达到…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...
