IEEE Latex模版踩雷避坑指南
- 参考文献
原Latex模版
\begin{thebibliography}{1}
\bibliographystyle{IEEEtran}\bibitem{ref1}
{\it{Mathematics Into Type}}. American Mathematical Society. [Online]. Available: https://www.ams.org/arc/styleguide/mit-2.pdf\bibitem{ref2}
T. W. Chaundy, P. R. Barrett and C. Batey, {\it{The Printing of Mathematics}}. London, U.K., Oxford Univ. Press, 1954.\bibitem{ref3}
F. Mittelbach and M. Goossens, {\it{The \LaTeX Companion}}, 2nd ed. Boston, MA, USA: Pearson, 2004.\bibitem{ref4}
G. Gr\"atzer, {\it{More Math Into LaTeX}}, New York, NY, USA: Springer, 2007.\bibitem{ref5}M. Letourneau and J. W. Sharp, {\it{AMS-StyleGuide-online.pdf,}} American Mathematical Society, Providence, RI, USA, [Online]. Available: http://www.ams.org/arc/styleguide/index.html\bibitem{ref6}
H. Sira-Ramirez, ``On the sliding mode control of nonlinear systems,'' \textit{Syst. Control Lett.}, vol. 19, pp. 303--312, 1992.\bibitem{ref7}
A. Levant, ``Exact differentiation of signals with unbounded higher derivatives,'' in \textit{Proc. 45th IEEE Conf. Decis.
Control}, San Diego, CA, USA, 2006, pp. 5585--5590. DOI: 10.1109/CDC.2006.377165.\bibitem{ref8}
M. Fliess, C. Join, and H. Sira-Ramirez, ``Non-linear estimation is easy,'' \textit{Int. J. Model., Ident. Control}, vol. 4, no. 1, pp. 12--27, 2008.\bibitem{ref9}
R. Ortega, A. Astolfi, G. Bastin, and H. Rodriguez, ``Stabilization of food-chain systems using a port-controlled Hamiltonian description,'' in \textit{Proc. Amer. Control Conf.}, Chicago, IL, USA,
2000, pp. 2245--2249.\end{thebibliography}
修改:创建bib文件,命名为refs.bib
打开谷歌学术

将内容复制到bib文件中

并在Latex文件后面写入
\bibliographystyle{IEEEtran}
\bibliography{refs}

相关文章:

IEEE Latex模版踩雷避坑指南
参考文献 原Latex模版 \begin{thebibliography}{1} \bibliographystyle{IEEEtran}\bibitem{ref1} {\it{Mathematics Into Type}}. American Mathematical Society. [Online]. Available: https://www.ams.org/arc/styleguide/mit-2.pdf\bibitem{ref2} T. W. Chaundy, P. R. Ba…...
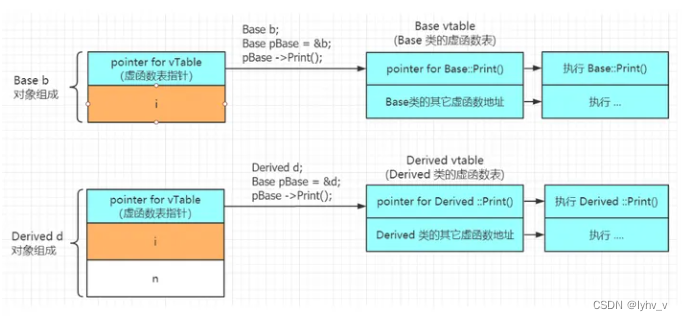
【C++】类与对象——多态详解
目录 一、多态的定义 二、重载、覆盖(重写)、隐藏(重定义)的对比 三、析构函数重写 四、C11 override 和 final 1. final 2. override 五、抽象类 六、多态的原理 一、多态的定义 多态是在不同继承关系的类对象,去调用同一函数,产生了不同的行为…...

WordPress建网站公司 建易WordPress建站
建易WordPress建网站公司是一家专业从事WordPress网站建设、网站维护、网站托管、运营推广和搜索引擎优化(SEO)等服务的公司。建易WordPress建网站公司提供多种服务,包括模板建站和定制网站,并且明码标价,价格透明,竭诚为全国各地…...

MySQL正则替换整个单词
\b 是正则表达式规定的一个特殊代码(好吧,某些人叫它元字符,metacharacter),代表着单词的开头或结尾,也就是单词的分界处。虽然通常英文的单词是由空格,标点符号或者换行来分隔的,但…...

Java设计模式:享元模式实现高效对象共享与内存优化(十一)
码到三十五 : 个人主页 目录 一、引言二、享元设计模式的概念1. 对象状态的划分2. 共享机制 三、享元设计模式的组成四、享元设计模式的工作原理五、享元模式的使用六、享元设计模式的优点和适用场景结语 [参见]: Java设计模式:核心概述&…...

景源畅信电商:抖音开店步骤是什么?
随着社交媒体的兴起,抖音已经成为一个不可忽视的电商平台。许多人都希望通过抖音开店来实现自己的创业梦想。那么,抖音开店的具体步骤是什么呢?接下来,我们将详细阐述这一问题。 一、明确回答问题抖音开店的步骤主要包括:注册账号…...
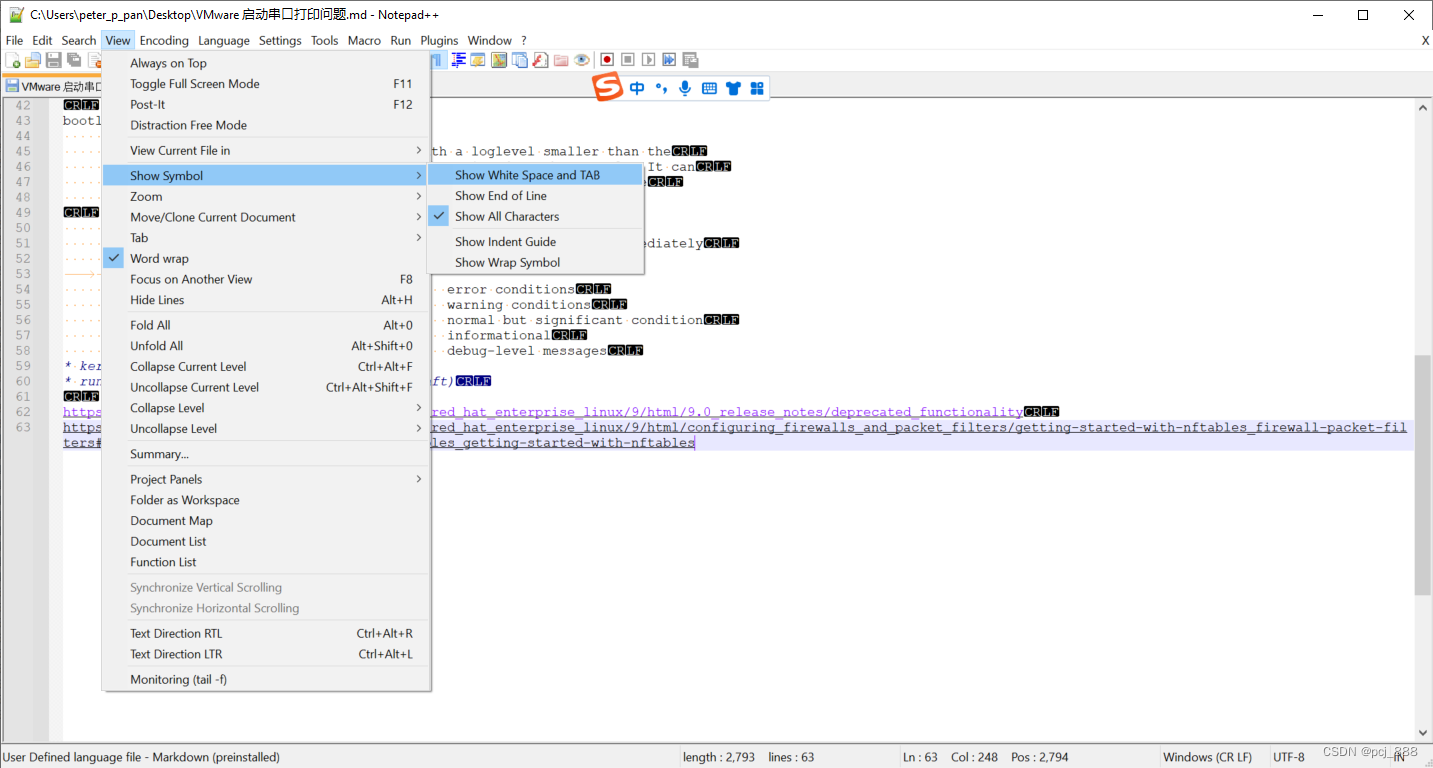
Notepad++不显示CRLF的方法
View -> Show Symbol -> 去掉勾选 Show All Characters...

前端开发工程师——AngularJS
一.表达式和语句 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice-w…...

【AI算法岗面试八股面经【超全整理】——概率论】
AI算法岗面试八股面经【超全整理】 概率论信息论机器学习CVNLP 目录 1、古典概型、几何概型2、条件概率、全概率公式、贝叶斯公式3、先验概率、后验概率4、离散型随机变量的常见分布5、连续型随机变量的常见分别6、数学期望、方差7、协方差、相关系数8、独立、互斥、不相关9.大…...
vue3 使用vant
使用前提: vite创建的vue3项目 vanthttps://vant-ui.github.io/vant/#/zh-CN/home npm i vant 引入样式: main.js import vant/lib/index.css vant封装 import { showLoadingToast,closeToast,showDialog,showConfirmDialog } from vant;export func…...

网络请求客户端WebClient的使用
在 Spring 5 之前,如果我们想要调用其他系统提供的 HTTP 服务,通常可以使用 Spring 提供的 RestTemplate 来访问,不过由于 RestTemplate 是 Spring 3 中引入的同步阻塞式 HTTP 客户端,因此存在一定性能瓶颈。根据 Spring 官方文档…...
unity制作app(9)--拍照 相册 上传照片
1.传输照片(任何较大的数据)都需要扩展服务器的内存空间。 2.还需要base64编码 2.1客户端发送位置的编码 2.2服务器接收部分的代码...
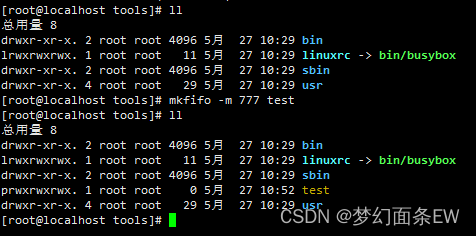
【busybox记录】【shell指令】mkfifo
目录 内容来源: 【GUN】【mkfifo】指令介绍 【busybox】【mkfifo】指令介绍 【linux】【mkfifo】指令介绍 使用示例: 创建管道文件 - 创建的时候同时指定文件权限 常用组合指令: 指令不常用/组合用法还需继续挖掘: 内容来…...

使用Jmeter进行性能测试的基本操作方法
🔥 交流讨论:欢迎加入我们一起学习! 🔥 资源分享:耗时200小时精选的「软件测试」资料包 🔥 教程推荐:火遍全网的《软件测试》教程 📢欢迎点赞 👍 收藏 ⭐留言 …...

Linux学习笔记(epoll,IO多路复用)
Linux learning note 1、epoll的使用场景2、epoll的使用方法和内部原理2.1、创建epoll2.2、使用epoll监听和处理事件 3、示例 1、epoll的使用场景 epoll的英文全称是extend poll,顾名思义是poll的升级版。常见的IO复用技术有select,poll,epo…...

STM32定时器及输出PWM完成呼吸灯
文章目录 一、STM32定时器原理1、基本定时器2、通用定时器(1)时钟源(2)预分频器PSC(3)计数器CNT(4)自动装载寄存器ARR 3、高级定时器 二、PWM工作原理三、控制LED以2s的频率周期性地…...

海外仓管理系统费用解析:如何选择高性价比的海外仓系统
海外仓作为链接国内商家和海外市场的重要环节,其重要性自然是不言而喻的。 对于众多中小型海外仓来说,如何在保证服务质量的同时降低运营成本,就成了大家关注的焦点。今天我们就从海外仓管理系统的费用这个角度,来帮助大家分析一…...

深度学习之学习率调度器Scheduler介绍
调度器是深度学习训练过程中非常重要的一部分,它用于动态调整模型的学习率,从而提高训练效率和最终性能。 1. 为什么需要学习率调度器? 深度学习训练中,学习率是一个非常关键的超参数。合适的学习率可以确保模型快速收敛并获得良好的性能。 但是在训练过程中,最优的学习率会随…...

蓝桥杯-AB路线(详细原创)
问题描述: 有一个由 N M 个方格组成的迷宫,每个方格写有一个字母 A 或者 B。小蓝站在迷宫左上角的方格,目标是走到右下角的方格。他每一步可以移动到上下左右相邻的方格去。 由于特殊的原因,小蓝的路线必须先走 K 个 A 格子、再…...

计算机字符编码的发展
目录 背景 发展 第一阶段:ASCII编码 第二阶段:扩展ASCII编码 第三阶段:各国编码 第四阶段:Unicode编码 第五阶段:UTF系列编码方式 相关扩展 背景 在计算机诞生初期,所有的数据都是基于二进制数&am…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
