Vue.js2+Cesium1.103.0 十六、多模型轨迹运动
Vue.js2+Cesium1.103.0 十六、多模型轨迹运动

Demo
<template><div id="cesium-container" style="width: 100%; height: 100%;"><ul class="ul"><li v-for="(item, index) of deviceInfo" :key="index" class="li" :class="{ active: lock === item.id }"@click="handleClick(item)">{{ `飞机${item.id}` }}</li></ul></div>
</template><script>
/* eslint-disable no-undef */
/* eslint-disable new-cap */
import DrawDeviceUtil from '@/utils/DrawDevice.js'
const mock = require('./mock.json')
const mock2 = require('./mock2.json')
const mock3 = require('./mock3.json')
const mock4 = require('./mock4.json')
const mock5 = require('./mock5.json')
export default {name: 'FlightAnimation',data () {return {lock: '',deviceInfo: [{id: 1,uri: 'model/Cesium_Air.glb',scale: 1,position: {longitude: mock[0].longitude,latitude: mock[0].latitude,altitude: mock[0].altitude}},{id: 2,uri: 'model/Cesium_Air.glb',scale: 0.9,position: {longitude: mock2[mock2.length - 1].longitude,latitude: mock2[mock2.length - 1].latitude,altitude: mock2[mock2.length - 1].altitude}},{id: 3,uri: 'model/Cesium_Air.glb',scale: 0.8,position: {longitude: mock3[mock3.length - 1].longitude,latitude: mock3[mock3.length - 1].latitude,altitude: mock3[mock3.length - 1].altitude}},{id: 4,uri: 'model/Cesium_Air.glb',scale: 1,position: {longitude: mock4[mock4.length - 1].longitude,latitude: mock4[mock4.length - 1].latitude,altitude: mock4[mock4.length - 1].altitude}},{id: 5,uri: 'model/Cesium_Air.glb',scale: 1,position: {longitude: mock5[mock5.length - 1].longitude,latitude: mock5[mock5.length - 1].latitude,altitude: mock5[mock5.length - 1].altitude}}],$DrawDeviceUtil: null}},computed: {},watch: {},mounted () {// returnwindow.$InitMap()viewer.camera.flyTo({destination: Cesium.Rectangle.fromDegrees(100, 10, 120, 70)})this.$DrawDeviceUtil = new DrawDeviceUtil()// * 添加设备this.$DrawDeviceUtil.AddDevices(this.deviceInfo)// * 模拟 ws 上报实时位置信息let count = 0setInterval(() => {count += 1const position = mock[count]const position2 = mock2[count]const position3 = mock3[count]const position4 = mock4[count]const position5 = mock5[count]// * 更新位置this.$DrawDeviceUtil.UpdatePosition(1, position)this.$DrawDeviceUtil.UpdatePosition(2, position2)this.$DrawDeviceUtil.UpdatePosition(3, position3)this.$DrawDeviceUtil.UpdatePosition(4, position4)this.$DrawDeviceUtil.UpdatePosition(5, position5)}, 300)// 鼠标事件const handler = new Cesium.ScreenSpaceEventHandler(viewer.scene.canvas)handler.setInputAction(function (event) { },Cesium.ScreenSpaceEventType.LEFT_CLICK)},methods: {handleClick (data) {this.lock = this.lock === data.id ? '' : data.idif (this.lock) {this.$DrawDeviceUtil.LockEntity(this.lock)} else {this.$DrawDeviceUtil.UnLockEntity()}}}
}
</script>
<style lang="scss" scoped>
.ul {position: absolute;right: 50px;top: 50px;z-index: 999;color: #fff;.li {cursor: pointer;&.active {color: red;}}
}
</style>
相关文章:

Vue.js2+Cesium1.103.0 十六、多模型轨迹运动
Vue.js2Cesium1.103.0 十六、多模型轨迹运动 Demo <template><div id"cesium-container" style"width: 100%; height: 100%;"><ul class"ul"><li v-for"(item, index) of deviceInfo" :key"index" cl…...
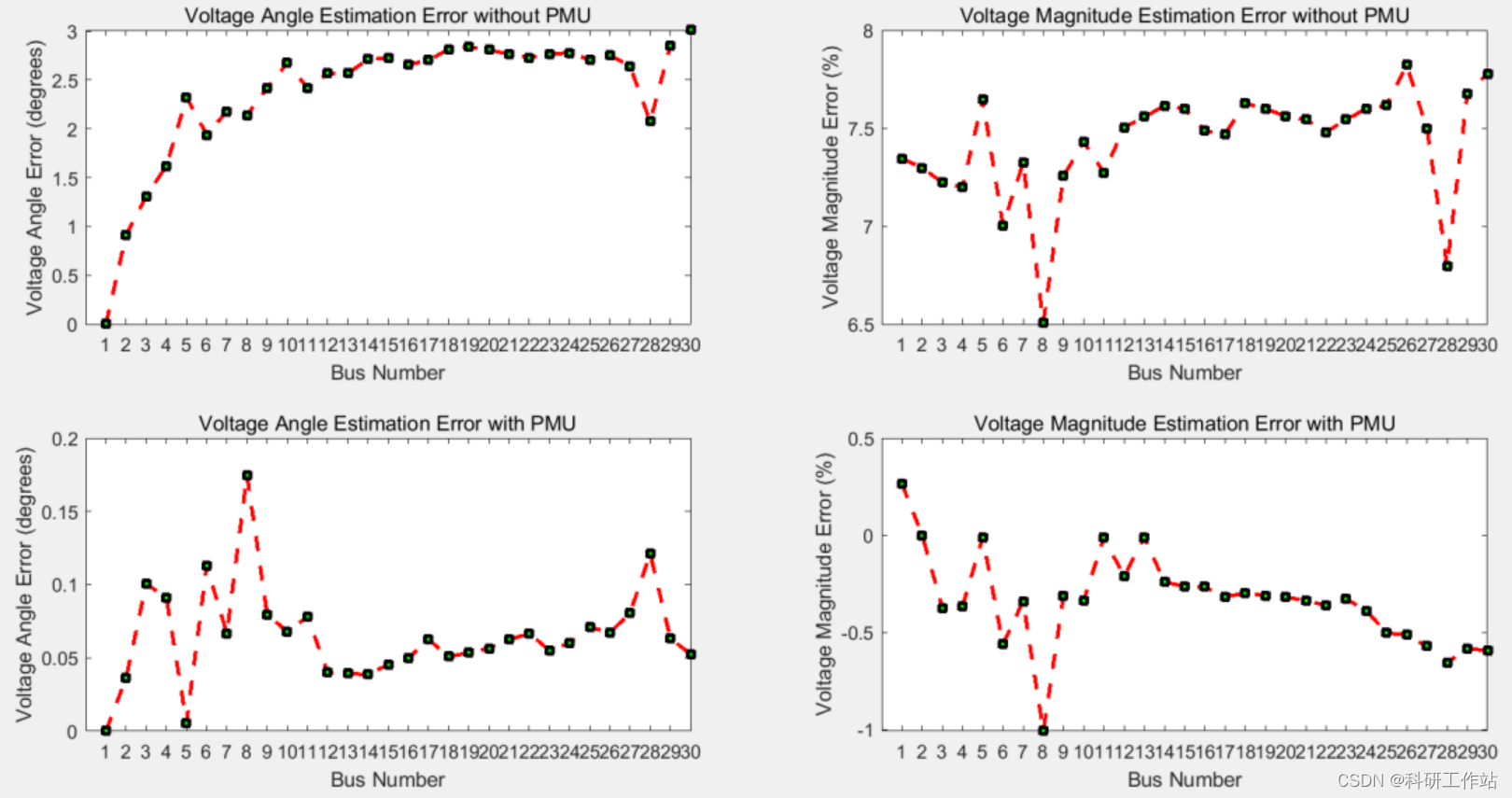
Matlab|基于PMU相量测量单元进行电力系统电压幅值和相角状态估计
主要内容 程序采用三种方法对14节点和30节点电力系统状态进行评估: ①PMU同步相量测量单元结合加权最小二乘法(WLS)分析电力系统的电压幅值和相角状态; ②并采用牛顿-拉夫逊方法进行系统潮流计算,结果作为理论分…...

【C++】---二叉搜索树
【C】---二叉搜索树 一、二叉搜索树概念二、二叉搜索树操作(非递归)1.二叉搜索树的查找 (非递归)(1)查找(2)中序遍历 2.二叉搜索树的插入(非递归)3.二叉搜索树…...

FastAPI - 依赖注入3
在FastAPI中,依赖注入是一种强大的功能,它允许你轻松地将依赖项注入到你的路由处理程序函数中,以处理不同的任务,例如数据库访问、认证和配置管理。 FastAPI支持依赖注入通过以下方式: 使用参数注解: 你可…...

【网络运维的重要性】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共…...
YOLOv5改进 | 注意力机制 | 添加双重注意力机制 DoubleAttention【附代码/涨点能手】
💡💡💡本专栏所有程序均经过测试,可成功执行💡💡💡 在图像识别中,学习捕捉长距离关系是基础。现有的CNN模型通常通过增加深度来建立这种关系,但这种形式效率极低。因此&…...

自用网站合集
总览 线上工具-图片压缩 TinyPNG线上工具-url参数解析 线上工具-MOV转GIF UI-Vant微信小程序版本其他-敏捷开发工具 Leangoo领歌 工具 线上工具-图片压缩 TinyPNG 不能超过5m,别的没啥缺点 线上工具-url参数解析 我基本上只用url参数解析一些常用的操作在线…...

【Golang】gin框架如何在中间件中捕获响应并修改后返回
【Golang】gin框架如何在中间件中捕获响应并修改后返回 本文讲述如何捕获中间件响应以及重写响应如果想在中间件中记录响应日志等操作,我们该如何获取响应数据呢?假如需要统一对响应数据做加密,如何修改这个返回数据再响应给客户端呢…...

电脑同时配置两个版本mysql数据库常见问题
1.配置时,要把bin中的mysql.exe和mysqld.exe 改个名字,不然两个版本会重复,当然,在初始化数据库的时候,如果时57版本的,就用mysql57(已经改名的)和mysqld57 代替 mysql 和 mysqld 例如 mysql -u root -p …...
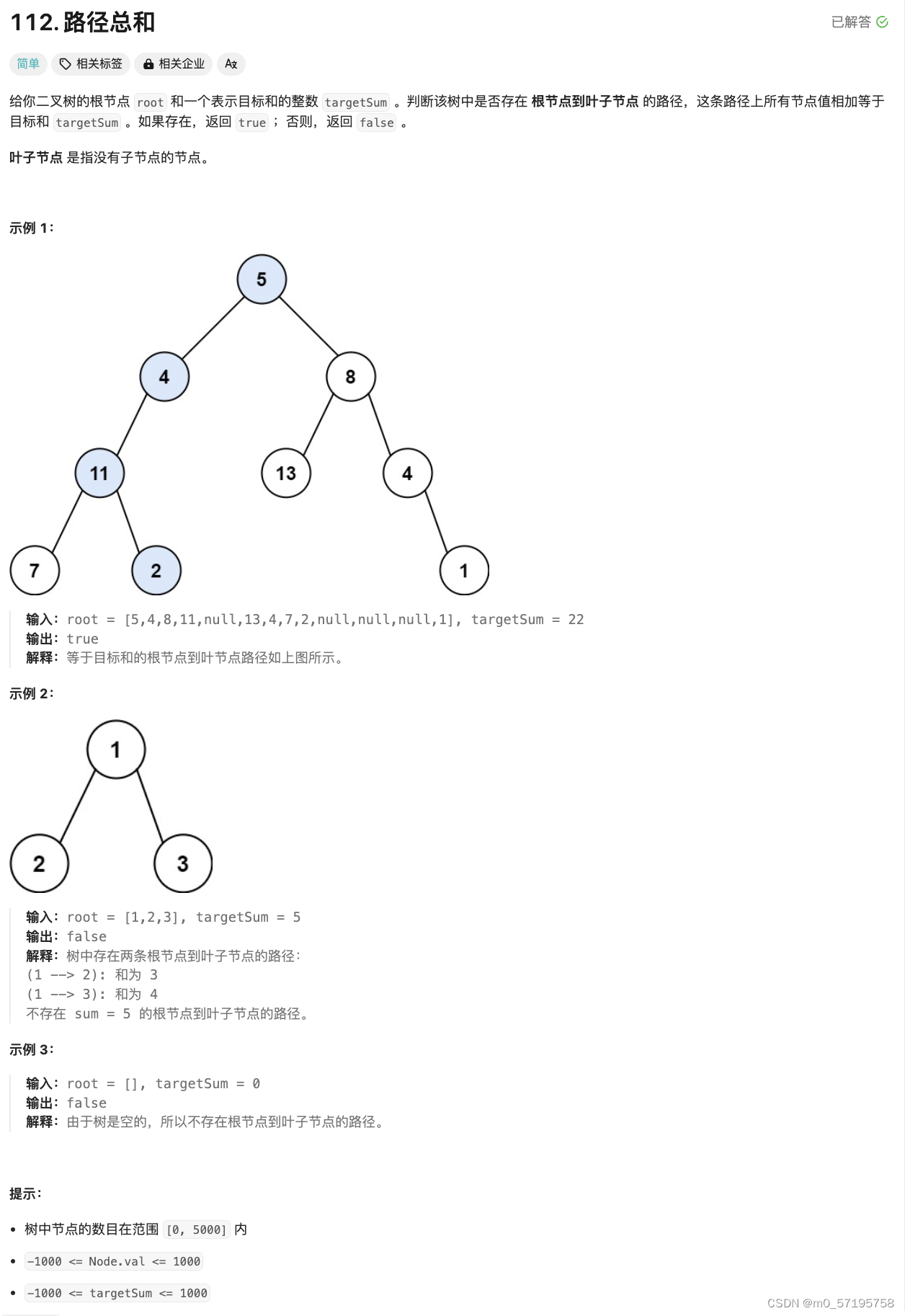
Java | Leetcode Java题解之第112题路径总和
题目: 题解: class Solution {public boolean hasPathSum(TreeNode root, int sum) {if (root null) {return false;}if (root.left null && root.right null) {return sum root.val;}return hasPathSum(root.left, sum - root.val) || has…...
HaloDB 的 Oracle 兼容模式
↑ 关注“少安事务所”公众号,欢迎⭐收藏,不错过精彩内容~ 前倾回顾 前面介绍了“光环”数据库的基本情况和安装办法。 哈喽,国产数据库!Halo DB! 三步走,Halo DB 安装指引 ★ HaloDB是基于原生PG打造的新一代高性能安…...

【Python】解决Python报错:TypeError: ‘xxx‘ object does not support item assignment
🧑 博主简介:阿里巴巴嵌入式技术专家,深耕嵌入式人工智能领域,具备多年的嵌入式硬件产品研发管理经验。 📒 博客介绍:分享嵌入式开发领域的相关知识、经验、思考和感悟,欢迎关注。提供嵌入式方向…...
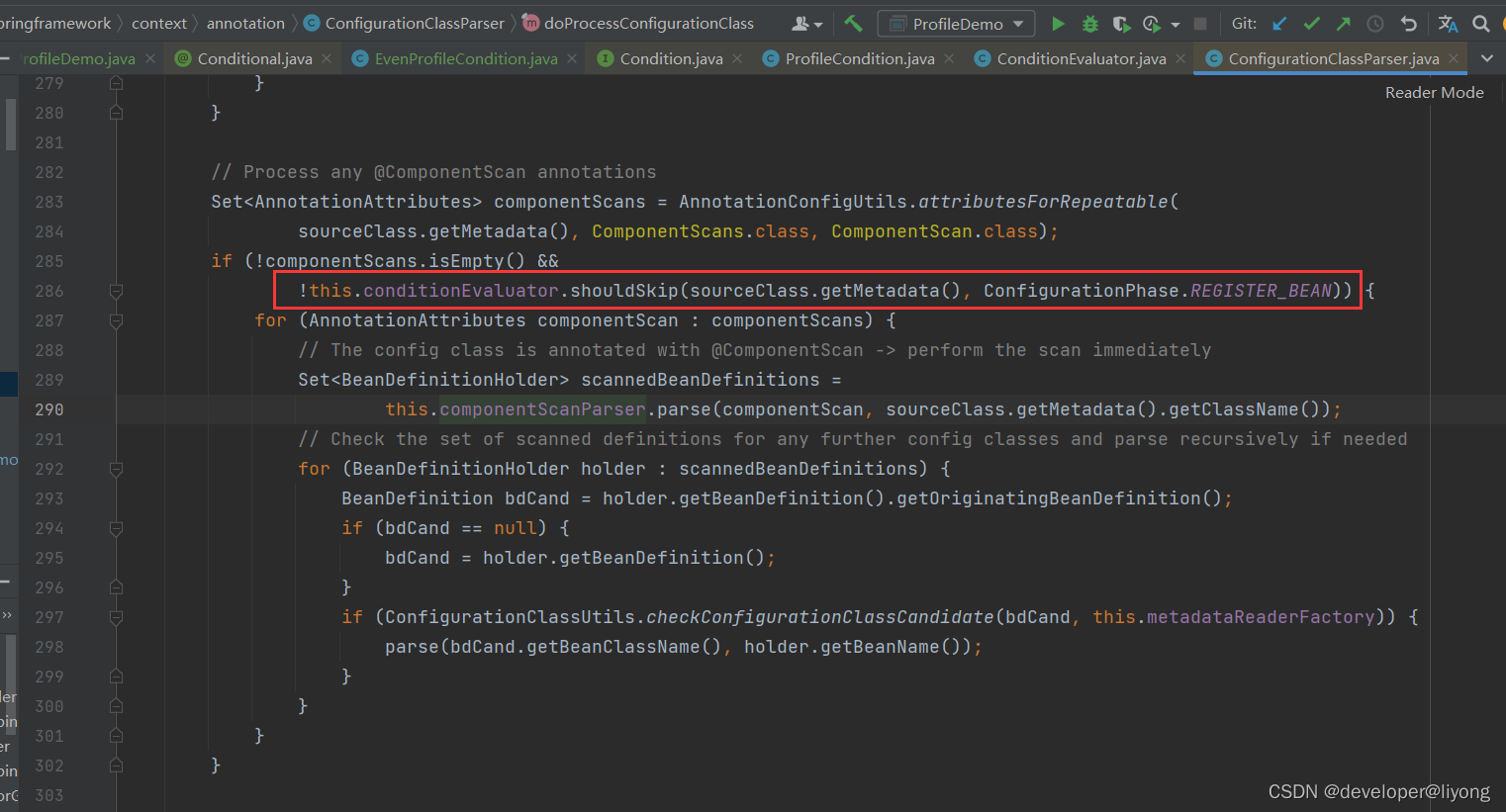
Spring-注解
Spring 注解分类 Spring 注解驱动模型 Spring 元注解 Documented Retention() Target() // 可以继承相关的属性 Inherited Repeatable()Spirng 模式注解 ComponentScan 原理 ClassPathScanningCandidateComponentProvider#findCandidateComponents public Set<BeanDefin…...

旧手机翻身成为办公利器——PalmDock的介绍也使用
旧手机有吧!!! 破电脑有吧!!! 那恭喜你,这篇文章可能对你有点用了。 介绍 这是一个旧手机废物利用变成工作利器的软件。可以在 Android 手机上快捷打开 windows 上的文件夹、文件、程序、命…...

期货交易的雷区
一、做自己看不懂的行情做交易计划一样要做有把握的,倘若你在盘中找机会交易,做自己看不懂的行情,即便你做进去了,建仓时也不会那么肯定,自然而然持仓也不自信,有点盈利就想平仓,亏损又想扛单。…...

东方通TongWeb结合Spring-Boot使用
一、概述 信创需要; 原状:原来的服务使用springboot框架,自带的web容器是tomcat,打成jar包启动; 需求:使用东方通tongweb来替换tomcat容器; 二、替换步骤 2.1 准备 获取到TongWeb7.0.E.6_P7嵌入版 这个文件,文件内容有相关对应的依赖包,可以根据需要来安装到本地…...
6.S081的Lab学习——Lab5: xv6 lazy page allocation
文章目录 前言一、Eliminate allocation from sbrk() (easy)解析: 二、Lazy allocation (moderate)解析: 三、Lazytests and Usertests (moderate)解析: 总结 前言 一个本硕双非的小菜鸡,备战24年秋招。打算尝试6.S081࿰…...
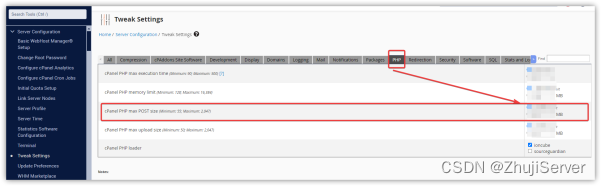
在WHM中如何调整max_post_size参数大小
今日我们在搭建新网站时需要调整一下PHP参数max_post_size 的大小,我们公司使用的Hostease的美国独立服务器产品默认5个IP地址,也购买了cPanel面板,因此联系Hostease的技术支持,寻求帮助了解到如何在WHM中调整PHP参数,…...

智能监控技术助力山林生态养鸡:打造智慧安全的养殖新模式
随着现代科技的不断发展,智能化、自动化的养殖方式逐渐受到广大养殖户的青睐。特别是在山林生态养鸡领域,智能化监控方案的引入不仅提高了养殖效率,更有助于保障鸡只的健康与安全。视频监控系统EasyCVR视频汇聚/安防监控视频管理平台在山林生…...

那些不起眼但很好玩的API合辑
那些不起眼但很好玩的API,为我们带来了许多出人意料的乐趣和惊喜。这些API可能看起来并不起眼,但它们却蕴含着无限的创意和趣味性。它们可以是一些小游戏API,让我们可以在闲暇时刻尽情娱乐;也可以是一些奇特的音乐API,…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
