算法入门----小话算法(1)
下面就首先从一些数学问题入手。
Q1: 如何证明时间复杂度O(logN) < O(N) < O(NlogN) < O(N2) < O(2N) < O(N!) < O(NN)?
A: 如果一个以整数为参数的不等式不能很容易看出不等的关系,那么最好用图示或者数学归纳法。
很显然,使用图示的方法也不能很好得到上面的关系图,因为图示范围较小,不能证明当N趋于无穷大依然成立。所以,数学归纳法成为首选。
不失一般性,假设logN的底数为2:
欲证明O(logN) < O(N),只需要证明log2N < N = log22N, 只需要证明N < 2N
当N = 1时成立,假设上面成立,现在只要证明N + 1 < 2N+1
这个显然成立。
O(N) < O(NlogN) 很容易证明,这里不再证明;
由O(logN) < O(N), 很容易证明 O(NlogN) < O(N2)
对于O(N2) < O(2N) < O(N!) < O(NN),由上面的方法同样很容易证明,这里不再赘述。
Q2:如何证明1+2+.....+n = n(n+1)/2 ?
A: 对于以整数n为变量的表达式的证明方式当然是数学归纳法。
当n=1时,很显然成立;假设等于n的时候也成立,下面就要证明当等于n+1的时候依然成立。
1+2+...+n+(n+1) = n(n+1)/2+(n+1)=(n+1)(n+2)/2.显然成立。所以证明此等式成立。
当然,证明这个还可以用高斯的NB计算方法:
假设S=1+2+...+(n-1)+n
同样S=n+(n-1)+...+2+1
所以两式相加: 2S=(n+1)+(n+1)+...+(n+1)+(n+1)=n(n+1);
所以S=n(n+1)/2.
当然,还有另外一种画图的方式来证明:
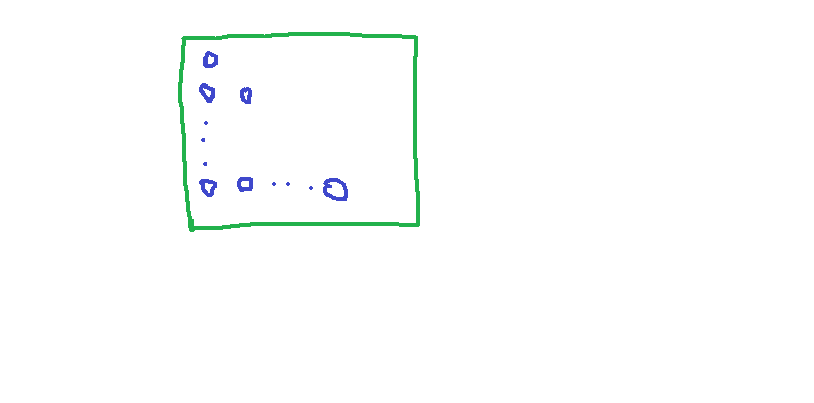
如上图,在一个边长为n的正方形里面,存放了1,2,...n这些小圆圈。
可以看出,(1+2+...+n)*2=n*n+n;
所以1+2+...+n=n(n+1)/2.
微风不燥,阳光正好,你就像风一样经过这里,愿你停留的片刻温暖舒心。
我是程序员小迷(致力于C、C++、Java、Kotlin、Android、Shell、JavaScript、TypeScript、Python等编程技术的技巧经验分享),若作品对您有帮助,请关注、分享、点赞、收藏、在看、喜欢,您的支持是我们为您提供帮助的最大动力。
欢迎关注。助您在编程路上越走越好!
相关文章:

算法入门----小话算法(1)
下面就首先从一些数学问题入手。 Q1: 如何证明时间复杂度O(logN) < O(N) < O(NlogN) < O(N2) < O(2N) < O(N!) < O(NN)? A: 如果一个以整数为参数的不等式不能很容易看出不等的关系,那么最好用图示或者数学归纳法。 很显…...

Vue | 自定义组件双向绑定基础用法
Vue | 自定义组件双向绑定基础用法 vue 中,由于单向数据流,常规的父子组件属性更新,需要 在父组件绑定相应属性,再绑定相应事件,事件里去做更新的操作,利用语法糖 可以减少绑定事件的操作。 这里就简单的梳…...

python使用modbustcp协议与PLC进行简单通信
AI应用开发相关目录 本专栏包括AI应用开发相关内容分享,包括不限于AI算法部署实施细节、AI应用后端分析服务相关概念及开发技巧、AI应用后端应用服务相关概念及开发技巧、AI应用前端实现路径及开发技巧 适用于具备一定算法及Python使用基础的人群 AI应用开发流程概…...

mongodb在游戏开发领域的优势
1、分布式id 游戏服务器里的大部分数据都是要求全局唯一的,例如玩家id,道具id。之所以有这种要求,是因为运营业务上需要进行合服操作,保证不同服的数据在进行合服之后,也能保证id不冲突。如果采用关系型数据库&#x…...

大数据Scala教程从入门到精通第十篇:Scala在IDEA中编写Hello World代码的简单说明
一:代码展示 object Main {def main(args: Array[String]): Unit {//SCALA中可以不写;//绿色的小三角达标的是这个类中有一个MAIN方法代表是可以执行的。//ctrl shift f10可以直接运行println("Hello world!")//Java中的类库我们可以直接使用System.o…...

【SPSS】基于因子分析法对水果茶调查问卷进行分析
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
ElasticSearch学习篇12_《检索技术核心20讲》基础篇
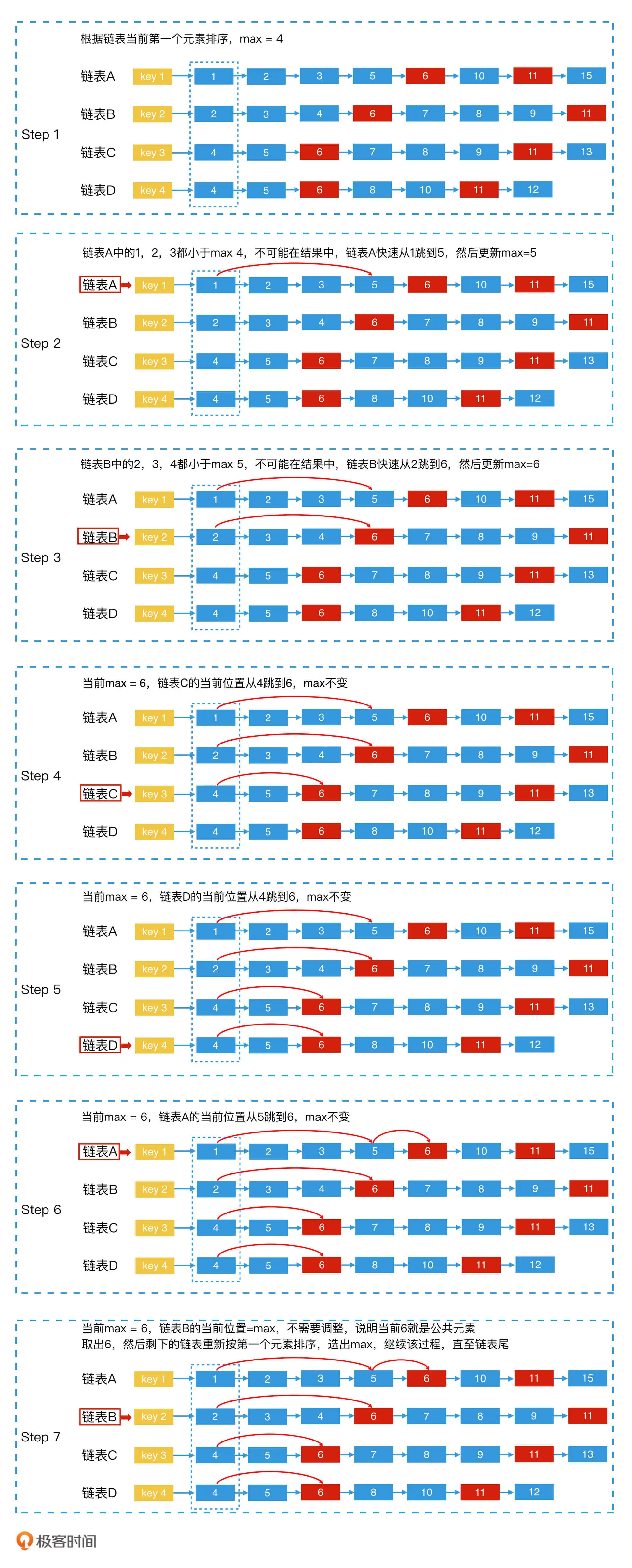
背景 学习极客实践课程《检索技术核心20讲》https://time.geekbang.org/column/article/215243 课程分为基础篇、进阶篇、系统案例篇 主要记录企业课程学习过程课程大纲关键点,以文档形式记录笔记。 内容 检索技术:它是更底层的通用技术,…...
Reids高频面试题汇总总结
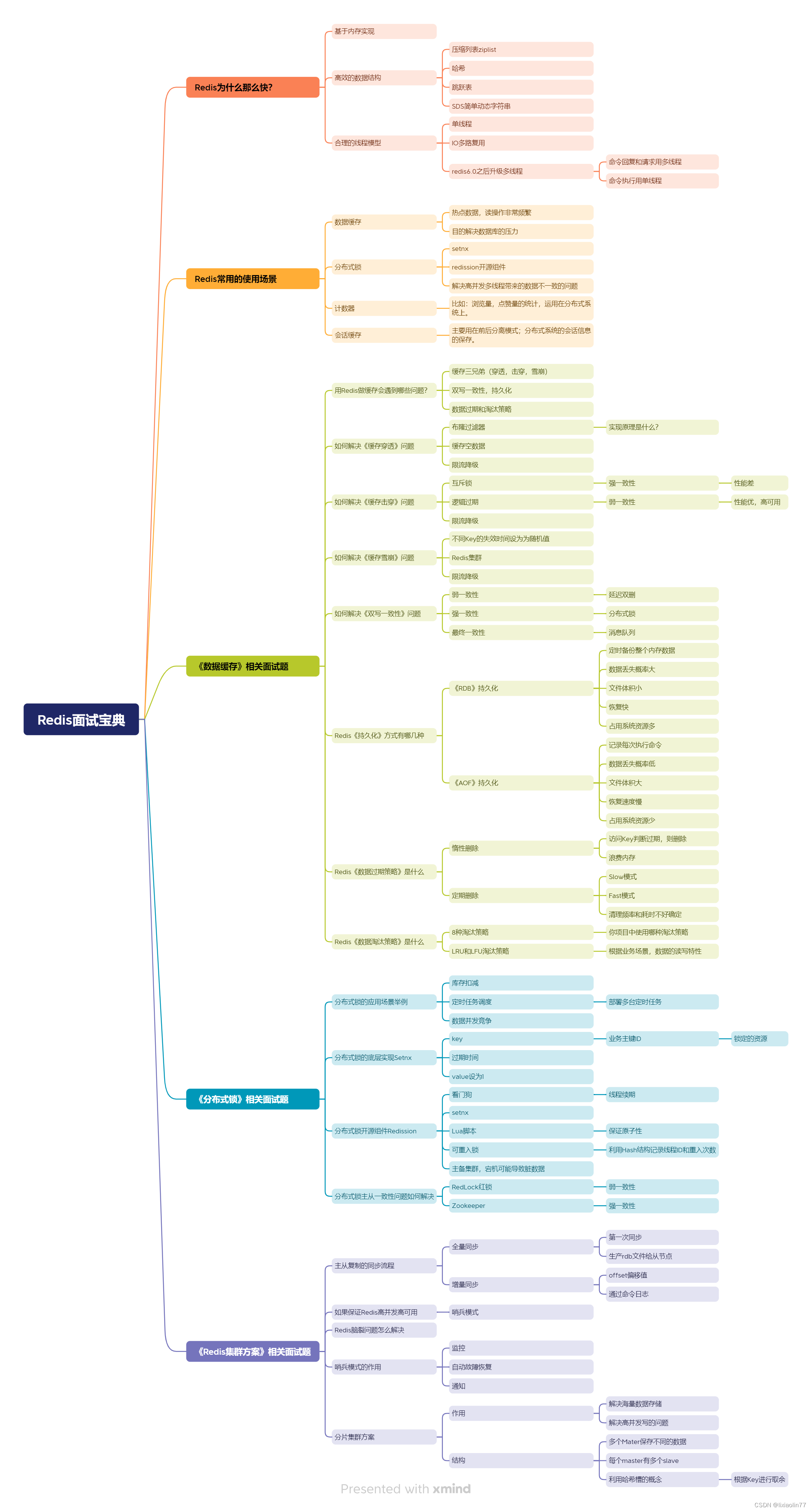
一、Redis基础 Redis是什么? Redis是一个开源的内存数据存储系统,它可以用作数据库、缓存和消息中间件。Redis支持多种数据结构,如字符串、哈希表、列表、集合、有序集合等,并提供了丰富的操作命令来操作这些数据结构。Redis的主要特点是什么? 高性能:Redis将数据存储在内…...
19 - grace数据处理 - 补充 - 地下水储量计算过程分解 - 冰后回弹(GIA)改正
19 - grace数据处理 - 补充 - 地下水储量计算过程分解 - 冰后回弹(GIA)改正 0 引言1 gia数据处理过程0 引言 由水量平衡方程可以将地下水储量的计算过程分解为3个部分,第一部分计算陆地水储量变化、第二部分计算地表水储量变化、第三部分计算冰后回弹改正、第四部分计算地下…...
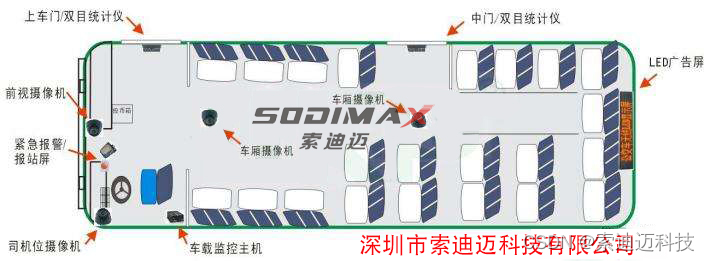
车载客流统计设备:双目3D还原智能统计算法的应用与优势
随着城市交通的日益繁忙和公共交通系统的不断完善,对公交车等交通工具的客流统计和分析变得越来越重要。传统的客流统计方法往往存在效率低下、精度不足等问题,难以满足现代城市交通管理的需求。而基于双目3D还原智能统计算法的车载客流统计设备…...
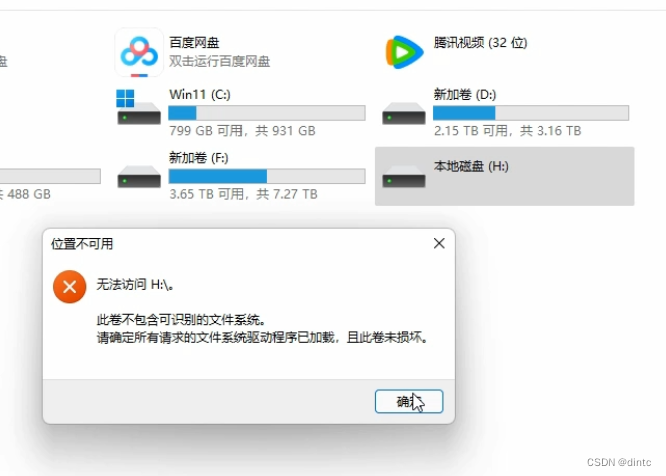
U盘无法打开?数据恢复与预防措施全解析
在日常生活和工作中,U盘已成为我们存储和传输数据的重要工具。然而,有时我们会遇到U盘无法打开的情况,这无疑给我们带来了诸多不便。本文将深入探讨U盘打不开的现象、原因及解决方案,并分享如何预防此类问题的发生。 一、U盘无法访…...

apollo版本更新简要概述
apollo版本更新简要概述 Apollo 里程碑版本9.0重要更新Apollo 开源平台 9.0 的主要新特征如下:基于包管理的 PnC 扩展开发范式基于包管理的感知扩展开发范式全新打造的 Dreamview Plus 开发者工具感知模型全面升级,支持增量训练 版本8.0版本6.0 Apollo 里…...

基于心电疾病分类的深度学习模型部署应用于OrangePi Kunpeng Pro开发板
一、开发板资源介绍 该板具有4核心64位的处理器和8TOPS的AI算力,让我们验证一下,在该板上跑深度学习模型的效果如何? 二、配网及远程SSH登录访问系统 在通过microusb连接串口进入开发板调试,在命令行终端执行以下命令 1&#…...

vue中axios的使用
1.get请求 axios.get(http://127.0.0.1:2333/show_course, {params: {param: choice} }) .then((response) > {this.list response.data; }) .catch((error) > {console.error(error); }); 2.post请求:当需要向服务器提交数据以创建新资源时使用。例如&…...

Spark SQL【Java API】
前言 之前对 Spark SQL 的影响一直停留在 DSL 语法上面,感觉可以用 SQL 表达的,没有必要用 Java/Scala 去写,但是面试一段时间后,发现不少公司还是在用 SparkSQL 的,京东也在使用 Spark On Hive 而不是我以为的 Hive O…...
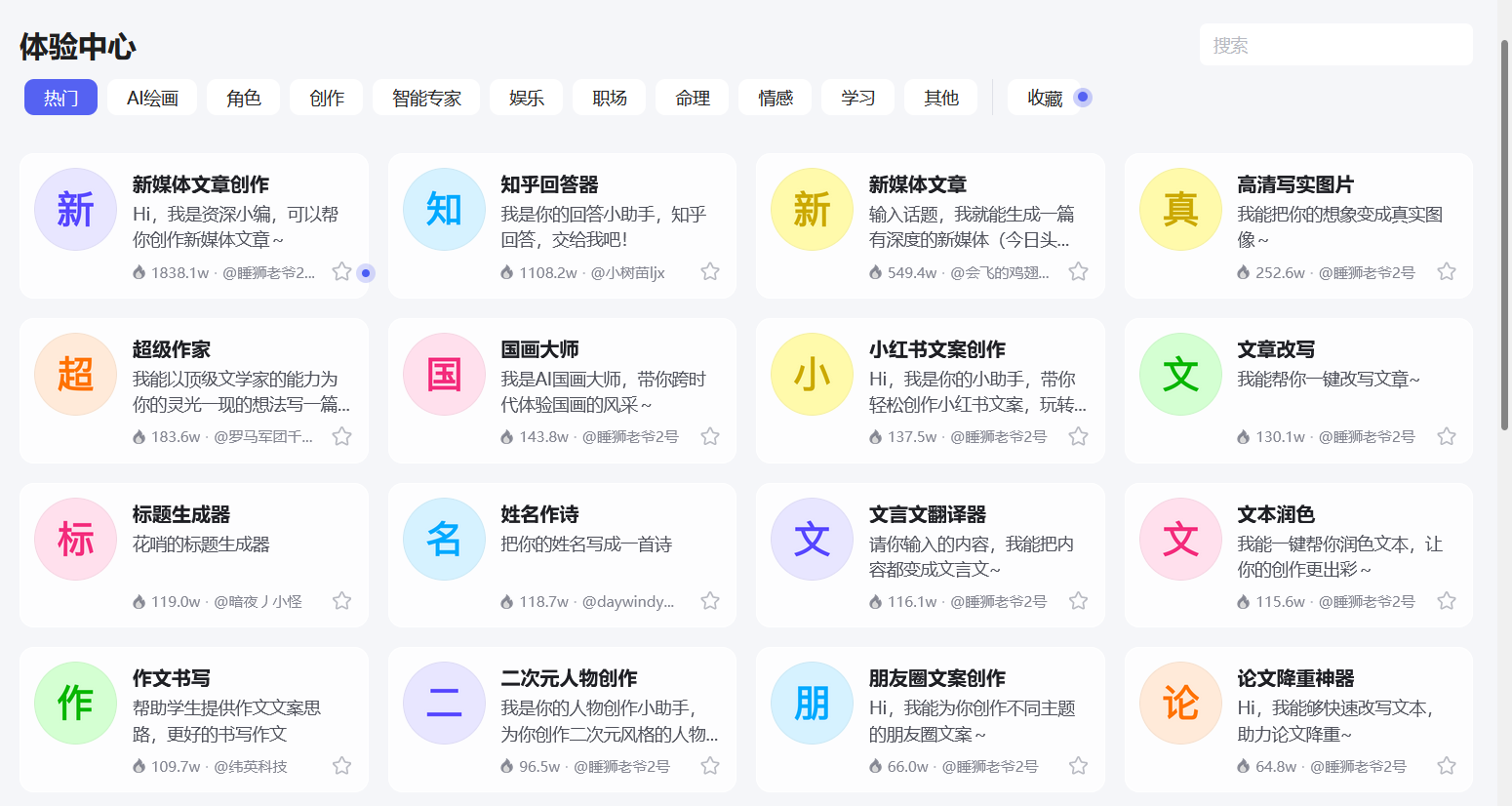
文心智能体平台丨创建你的四六级学习小助手
引言 在人工智能飞速发展的今天,我们迎来了文心智能体平台。该平台集成了最先进的人工智能技术,旨在为用户提供个性化、高效的学习辅助服务。今天,我们将向大家介绍如何利用文心智能体平台,创建一个专属于你的四六级学习小助手。…...
)
js全国省市区JSON数据(全)
AreaJson 就是全国省市区的具体数据信息,下面我自定义了一些方法,获取数据用的,不需要的可以删掉,只拿JSON内的数据即可 const AreaJson [{"name": "北京市","city": [{"name": "…...

轻量级 C Logger
目录 一、描述 二、实现效果 三、使用案例 四、内存检测 一、描述 最近实现一个 WS 服务器,内部需要一个日志打印记录服务器程序的运行过程,故自己实现了一个轻量级的 logger,主要包含如下特征: 可输出 debug、info、warn、er…...

哪里能下载到合适的衣柜3D模型素材?
室内设计师在进行家居设计时,衣柜3D模型素材是非常重要的工具。那么,哪里能下载到合适的衣柜3D模型素材呢? 一、建e网: ①建e网是一个专注于3D模型素材分享的平台,上面可以找到大量的衣柜3D模型。 ②该网站提供的模型种类丰富&am…...

计算机毕业设计 | SpringBoot+vue仓库管理系统(附源码)
1,绪论 1.1 项目背景 随着电子计算机技术和信息网络技术的发明和应用,使着人类社会从工业经济时代向知识经济时代发展。在这个知识经济时代里,仓库管理系统将会成为企业生产以及运作不可缺少的管理工具。这个仓库管理系统是由:一…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...

Ansible+Zabbix-agent2快速实现对多主机监控
ansible Ansible 是一款开源的自动化工具,用于配置管理(Configuration Management)、应用部署(Application Deployment)、任务自动化(Task Automation)和编排(Orchestration…...

CMake系统学习笔记
CMake系统学习笔记 基础操作 最基本的案例 // code #include <iostream>int main() {std::cout << "hello world " << std::endl;return 0; }// CMakeLists.txt cmake_minimum_required(VERSION 3.0)# 定义当前工程名称 project(demo)add_execu…...
