从零开始学习Slam-旋转矩阵旋转向量四元组(二)
本文参考:计算机视觉life 仅作笔记用
书接上回,上回不清不楚的介绍了旋转矩阵&旋转向量和四元组
现在回顾一下重点:
本着绕谁谁不变的变则
假设绕z轴旋转θ,旋转矩阵为:
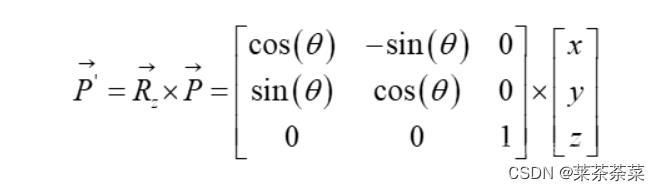
再回顾一下旋转向量的表示以及这个基本记不住的罗德里格斯公式,记不住也没事:

一个例子
已知旋转矩阵定义是沿着Z轴旋转45°。请按照该定义初始化旋转向量、旋转矩阵、四元数、欧拉角。请编程实现:
1、以上四种表达方式的相互转换关系并输出,并参考给出的结果验证是否正确。
2、假设平移向量为(1,2,3),请输出旋转矩阵和该平移矩阵构成的欧式变换矩阵,并根据欧式变换矩阵提取旋转向量及平移向量。
#include <iostream>
#include <Eigen/Dense>using namespace Eigen;int main() {// 初始化旋转参数double angle = M_PI/4; // 45°转换为弧度Vector3d axis = Vector3d::UnitZ(); // Z轴// 初始化旋转向量Vector3d rotation_vector = angle * axis;// 初始化旋转矩阵Matrix3d rotation_matrix;// AngleAxisd(angle, axis) 创建了一个表示绕着给定轴 axis 旋转 angle 弧度的旋转向量。//在Eigen库中,AngleAxisd 类表示一个旋转向量,它由一个旋转轴和一个旋转角度组成。//它的构造函数可以接受旋转角度和旋转轴作为参数,也可以接受一个旋转矩阵作为参数,并从中提取旋转轴和旋转角度。//调用 toRotationMatrix() 方法将该旋转向量转换为对应的旋转矩阵。rotation_matrix = AngleAxisd(angle, axis).toRotationMatrix();// 初始化四元数Quaterniond quaternion(rotation_matrix);// 初始化欧拉角Vector3d euler_angles = rotation_matrix.eulerAngles(2, 1, 0); // ZYX顺序// 输出四种表达方式 // 旋转向量std::cout << "Rotation Vector: " << rotation_vector.transpose() << std::endl; // .transpose()方法被用于将向量和矩阵输出成为行向量的形式,以方便显示在控制台上。// 旋转矩阵std::cout << "Rotation Matrix:\n" << rotation_matrix << std::endl;// coeffs()方法用于获取四元数对象的系数,返回一个四维向量。std::cout << "Quaternion: " << quaternion.coeffs()<< std::endl;// 欧拉角std::cout << "Euler Angles (ZYX): " << euler_angles.transpose() << std::endl;// 假设平移向量为(1,2,3)Vector3d translation_vector(1, 2, 3);// 构造欧式变换矩阵Matrix4d euclidean_transform_matrix = Matrix4d::Identity(); // 创建一个4x4的单位矩阵的静态方法// 将旋转矩阵赋值给欧几里德变换矩阵的左上角的3x3子矩阵,即旋转部分euclidean_transform_matrix.block<3,3>(0,0) = rotation_matrix;// 将平移向量赋值给欧几里德变换矩阵的右上角的3x1子矩阵,即平移部分euclidean_transform_matrix.block<3,1>(0,3) = translation_vector;/* 在Eigen库中,AngleAxisd()是用于创建一个旋转向量(Angle-Axis)的构造函数。Angle-Axis旋转表示通过一个旋转轴和一个旋转角度来描述旋转。具体来说,AngleAxisd()的使用方法如下Eigen::AngleAxisd angle_axis(angle, axis);在这段代码中,AngleAxisd(rotation_matrix)创建了一个AngleAxisd类型的对象,该对象代表了由旋转矩阵rotation_matrix表示的旋转。然后,.axis()方法用于获取该旋转向量的旋转轴,而.angle()方法用于获取旋转角度。接着,AngleAxisd(rotation_matrix).axis() * AngleAxisd(rotation_matrix).angle()部分将旋转向量的轴乘以旋转角度,这将得到一个旋转向量,其方向由旋转轴决定,大小由旋转角度决定。这个旋转向量被赋值给了extracted_rotation_vector。*/// 从欧式变换矩阵分解出旋转向量和平移向量Vector3d extracted_rotation_vector = AngleAxisd(rotation_matrix).axis() * AngleAxisd(rotation_matrix).angle();/* block<3,1>(0,3)是Eigen库中的一个函数,用于从矩阵中提取特定的块。在这里,block<3,1>(0,3)表示提取了从第0行开始,第3列开始的一个3x1的块,即欧氏变换矩阵的前三个元素(0, 1, 2行,3列),这通常是表示平移向量的部分。*/ Vector3d extracted_translation_vector = euclidean_transform_matrix.block<3,1>(0,3);// 输出欧式变换矩阵、提取的旋转向量和平移向量// 欧式变换矩阵std::cout << "\nEuclidean Transformation Matrix:\n" << euclidean_transform_matrix << std::endl;// 旋转向量std::cout << "Extracted Rotation Vector: " << extracted_rotation_vector.transpose() << std::endl;// 平移向量std::cout << "Extracted Translation Vector: " << extracted_translation_vector.transpose() << std::endl;return 0;
}多看几遍代码,俺就算基本入第一道门了。。。
相关文章:

从零开始学习Slam-旋转矩阵旋转向量四元组(二)
本文参考:计算机视觉life 仅作笔记用 书接上回,上回不清不楚的介绍了旋转矩阵&旋转向量和四元组 现在回顾一下重点: 本着绕谁谁不变的变则 假设绕z轴旋转θ,旋转矩阵为: 再回顾一下旋转向量的表示以及这个基本记不…...

基于Spring Security添加流控
基于Spring Security添加流控的过程: 步骤1: 添加依赖 确保项目中包含了Spring Security和Sentinel-Core的相关依赖。在Maven项目中,可以在pom.xml中添加如下依赖: <!-- Spring Security --> <dependency><groupId>org.…...
Python | Leetcode Python题解之第119题杨辉三角II
题目: 题解: class Solution:def getRow(self, rowIndex: int) -> List[int]:row [1, 1]if rowIndex < 1:return row[:rowIndex 1]elif rowIndex > 2:for i in range(rowIndex - 1):row [row[j] row[j 1] for j in range(i 1)]row.inser…...

物联网应用系统与网关
一. 传感器底板相关设计 1. 传感器设计 立创EDA传感器设计举例。 2. 传感器实物图 3. 传感器测试举例 测试激光测距传感器 二. 网关相关设计 1. LORA,NBIOT等设计 2. LORA,NBIOT等实物图 3. ZigBee测试 ZigBee测试 4. NBIoT测试 NBIoT自制模块的测试…...

系统稳定性概览
系统稳定性 系统稳定性,包括:监控、 告警、性能优化、慢sql、耗时接口等。 系统的稳定性的治理,可以围绕这几方面展开。 监控 Prometheus 监控并收集数据。监控 qps,tps, rt , cpu使用率,cpu load&#…...

Redis-Cluster模式基操篇
一、场景 1、搞一套6个主节点的Cluster集群 2、模拟数据正常读写 3、模拟单点故障 4、在不停服务的情况下将集群架构改为3主3从 二、环境规划 6台独立的服务器,端口18001~18006 192.169.14.121 192.169.14.122 192.169.14.123 192.169.14.124 192.169.14.125 192…...
Golang | Leetcode Golang题解之第113题路径总和II
题目: 题解: type pair struct {node *TreeNodeleft int }func pathSum(root *TreeNode, targetSum int) (ans [][]int) {if root nil {return}parent : map[*TreeNode]*TreeNode{}getPath : func(node *TreeNode) (path []int) {for ; node ! nil; no…...
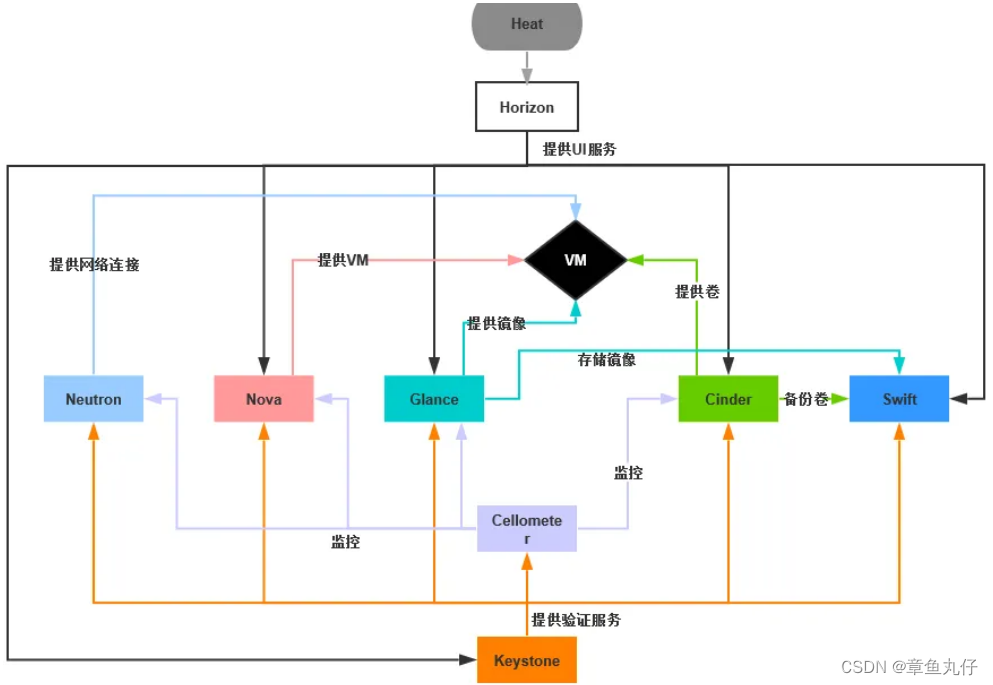
云计算与 openstack
文章目录 一、 虚拟化二、云计算2.1 IT系统架构的发展2.2 云计算2.3 云计算的服务类型 三、Openstack3.1 OpenStack核心组件 一、 虚拟化 虚拟化使得在一台物理的服务器上可以跑多台虚拟机,虚拟机共享物理机的 CPU、内存、IO 硬件资源,但逻辑上虚拟机之…...
golang语言的gofly快速开发框架如何设置多样的主题说明
本节教大家如何用gofly快速开发框架后台内置设置参数,配置出合适项目的布局及样式、主题色,让你您的项目在交互上加分,也是能帮你在交付项目时更容易得到客户认可,你的软件使用客户他们一般都是不都技术的,所以当他们拿…...
lynis安全漏洞扫描工具
Lynis是一款Unix系统的安全审计以及加固工具,能够进行深层次的安全扫描,其目的是检测潜在的时间并对未来的系统加固提供建议。这款软件会扫描一般系统信息,脆弱软件包以及潜在的错误配置。 安装 方式1 git下载使用git clone https://github…...
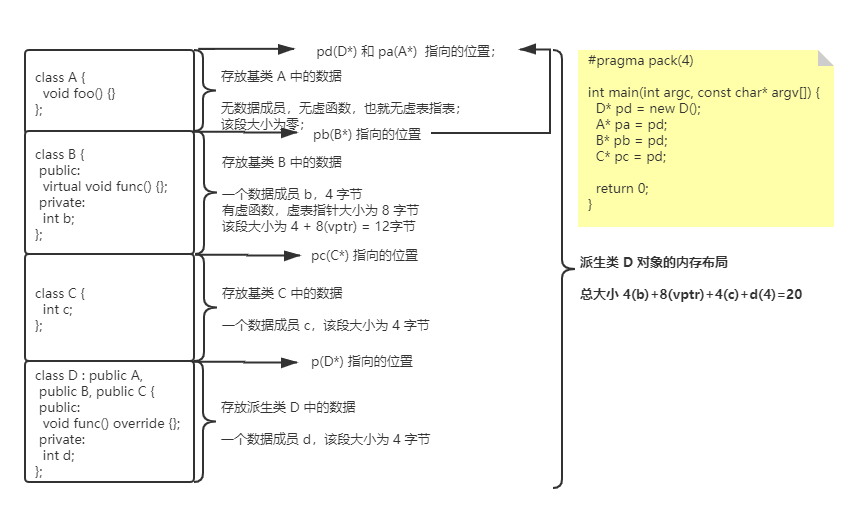
C++ 多重继承的内存布局和指针偏移
在 C 程序里,在有多重继承的类里面。指向派生类对象的基类指针,其实是指向了派生类对象里面,该基类对象的起始位置,该位置相对于派生类对象可能有偏移。偏移的大小,等于派生类的继承顺序表里面,排在该类前面…...

centos时间不对
检查当前时区是否正确 timedatectl status如果时区不正确,使用以下命令设置正确的时区(将Asia/Shanghai替换为您所在的时区): timedatectl set-timezone Asia/Shanghai如果时区正确但时间不准确,使用以下命令同步网络…...

通过Redis实现防止接口重复提交功能
本功能是在切面执行链基础上实现的功能,如果不知道切面执行链的同学,请看一下我之前专门介绍切面执行链的文章。 在SpringBoot项目中实现切面执行链功能-CSDN博客 1.定义防重复提交handler /*** 重复提交handler**/ AspectHandlerOrder public class …...

如何构建最小堆?
方式1:上浮调整 /*** 上浮调整(小的上浮)*/ public static void smallUp1(int[] arr, int child) {int parent (child - 1) / 2;while (0 < child && arr[child] < arr[parent]) { // 0 < child说明这个节点还是叶子arr[child] arr[child] ^ ar…...
客户端)
基于Netty实现安全认证的WebSocket(wss)客户端
1.Netty服务端 服务端代码参考【基于Netty实现安全认证的WebSocket(wss)服务端-CSDN博客】 2.Netty客户端 客户端代码参考【基于Netty实现WebSocket客户端-CSDN博客】中两种都可以;这里用的是第一种。 新增SslHandler的代码: …...
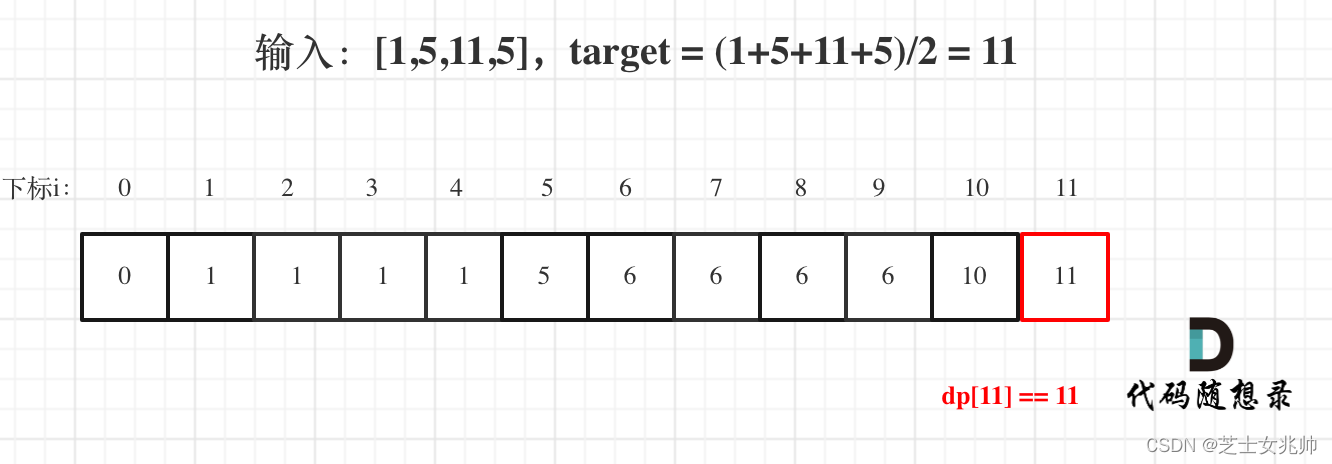
代码随想录算法训练营第四十四天 | 01背包问题 二维、 01背包问题 一维、416. 分割等和子集
01背包问题 二维 代码随想录 视频讲解:带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili 1.dp数组定义 dp[i][j] 下标为[0,i]之间的物品&…...

redis常见使用场景
文章目录 redis常见使用场景全局ID位统计购物车用户消息时间线timeline抽奖商品筛选分布式锁限流redis实现计数器排行榜消息队列redis 如何实现延时队列 redis生产常用的场景 redis常见使用场景 Redis 是一种高性能的内存数据库,广泛应用于各种场景中。以下是 Redi…...
算法更新公式推导)
模糊C均值(FCM)算法更新公式推导
模糊C均值(FCM)算法更新公式推导 目标函数 FCM的目标函数为: J m ∑ i 1 n ∑ j 1 k u i j m ∥ x i − c j ∥ 2 J_m \sum_{i1}^n \sum_{j1}^k u_{ij}^m \|x_i - c_j\|^2 Jmi1∑nj1∑kuijm∥xi−cj∥2 其中: …...

金融创新浪潮下的拆分盘投资探索
随着数字化时代的步伐加速,金融领域正经历着前所未有的变革。在众多金融创新中,拆分盘作为一种新兴的投资模式,以其独特的增长机制,吸引了投资者的广泛关注。本文将对拆分盘的投资逻辑进行深入剖析,并结合具体案例&…...

一份不知道哪里来的第十五届国赛模拟题
这是一个不知道来源的模拟题目,没有完全完成,只作代码记录,不作分析和展示,极其冗长,但里面有长按短按双击的复合,可以看看。 目录 题目代码底层驱动主程序核心代码关键:双击单击长按复合代码 …...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
