当前位置： 首页 > news >正文

解决Windows 10通过SSH连接Ubuntu 20.04时的“Permission Denied”错误

news 2026/5/16 11:46:14

在使用SSH连接远程服务器时，我们经常可能遇到各种连接错误，其中“Permission denied, please try again”是较为常见的一种。本文将分享一次实际案例的解决过程，帮助你理解如何排查并解决这类问题。

问题描述

在尝试从Windows 10系统通过SSH连接到Ubuntu 20.04服务器时，不断出现“Permission denied, please try again”的错误消息。这类问题通常与SSH认证相关。

错误原因

经过仔细检查，发现问题的根本原因在于SSH配置文件中的用户名不正确。在Ubuntu的命令行界面显示的用户名是jjj@jjjiang，这表明正确的用户名应为jjj，而不是我之前在Windows上配置的jjjiang。
在这里插入图片描述

解决步骤

  1. 检查用户名：首先确认Ubuntu系统中有效的用户名，可以通过查看命令提示符或者whoami命令来确认当前登录的用户名。

  2. 修改SSH配置：在Windows系统中，找到用于SSH连接的配置文件（通常位于~/.ssh/config），将用户名从jjjiang更改为jjj。
    在这里插入图片描述

  3. 重新连接：修改配置后，重新发起SSH连接尝试。

结果

更正用户名后，再次尝试连接时成功，且连接过程中不再要求输入密码，表明之前的认证问题已经解决。

总结

SSH连接问题很常见，但通过系统地检查配置和认证方式，大多数问题都可以被解决。在遇到“Permission denied”类的错误时，务必先从用户名和密码认证设置入手，这往往是问题的关键所在。

希望这篇文章能帮助你解决SSH连接中可能遇到的问题！如果有更多问题或需要进一步的帮助，欢迎留言交流。

相关文章：

解决Windows 10通过SSH连接Ubuntu 20.04时的“Permission Denied”错误

在使用SSH连接远程服务器时，我们经常可能遇到各种连接错误，其中“Permission denied, please try again”是较为常见的一种。本文将分享一次实际案例的解决过程，帮助你理解如何排查并解决这类问题。 问题描述 在尝试从Windows 10系统通过SS…...

编程日记 2024/6/1 11:41:01

Windows 下 PostgreSQL 图形化界面安装、配置详解

相信大家对PostgreSQL都不陌生吧，自从MySQL被Oracle所控制后，PostgreSQL就成为了国内去O的首选数据库了，并且PostgreSQL目前不受任何商业公司控制，所以国内很多厂商都是基于PostgreSQL做二次开发来实现数据库自主可控的目标(国内很…...

编程日记 2024/6/1 11:37:58

曾巩，散文的艺术与哲思

曾巩，字子固，世称南丰先生，南丰（今江西）人，生于北宋真宗天禧三年（公元1019年），卒于北宋元丰六年（公元1083年），享年64岁。他是中国北宋…...

编程日记 2024/6/1 11:36:57

【SpringBoot】怎么在一个大的SpringBoot项目中创建多个小的SpringBoot项目，从而形成子父依赖

父子项目工程创建 步骤 先创建父项目 具体操作步骤请看本文章：使用maven工程创建spring boot项目 创建子项目 file- project structure module–new module 剩下步骤请看创建父工程时的操作使用maven工程创建spring boot项目 应用 确认即可 之后创建启动类…...

编程日记 2024/6/1 11:35:56

vue3组件通信与props

title: vue3组件通信与props date: 2024/5/31 下午9:00:57 updated: 2024/5/31 下午9:00:57 categories: 前端开发 tags: Vue3组件Props详解生命周期数据通信模板语法Composition API单向数据流 Vue 3 组件基础 在 Vue 3 中，组件是构建用户界面的基本单位&#…...

编程日记 2024/6/1 11:34:55

并发和异步编程:详细概述

01 Concurrency and Asynchronous Programming: a Detailed Overview 并发和异步编程:详细概述 Asynchronous programming is one of those topics many programmers find confusing. You come to the point when you think you’ve got it, only to later realize that the …...

编程日记 2024/6/1 11:30:51

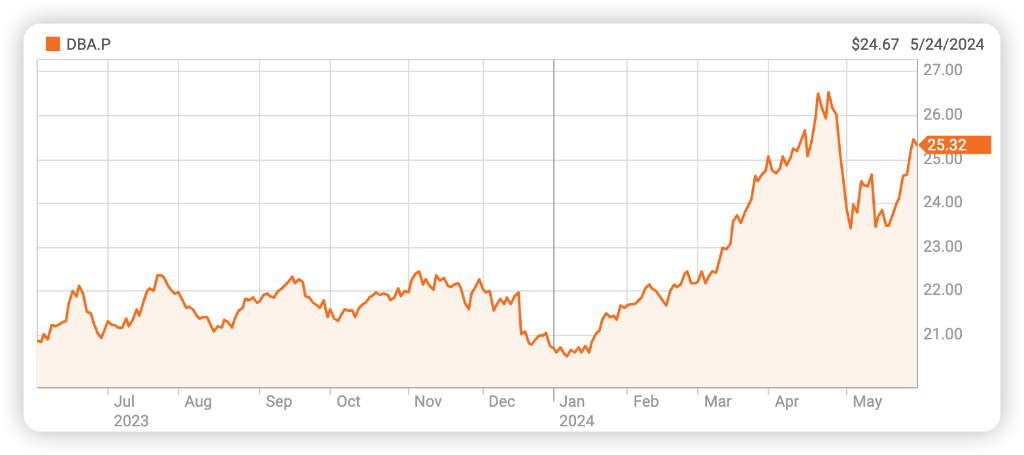
交易员摩拳擦掌，就在今年夏天，极端气候引爆商品？

有史以来最严重的高温炙烤下，从农业到能源到航运都可能受到严重负面影响，大宗商品市场波动将大幅加剧。 2024年有望成为有史以来最炎热的一年，随着北半球步入夏季，世界各地都将遭受由全球变暖造成的极端高温困扰。极端天气不仅给民…...

编程日记 2024/6/1 11:29:50

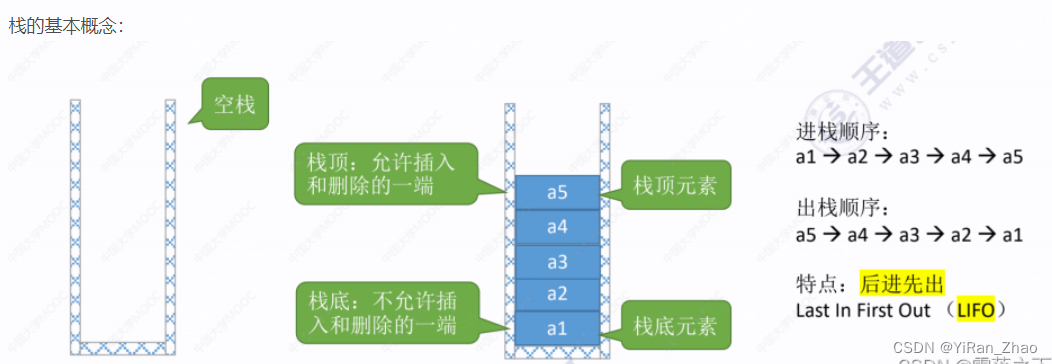
数据结构学习笔记

1. 数组 (Array) 定义 数组是一种线性数据结构，用于存储固定大小的相同类型元素集合。每个元素都有一个索引，用于快速访问。 特点 优点：访问速度快，通过索引直接访问O(1)时间复杂度。缺点：大小固定，插入…...

编程日记 2024/6/1 11:28:48

vscode导入自定义模块报错ModuleNotFoundError解决方案

问题描述 我的项目为great_gas_or_agents，目录结构如下： log_data_extract main.py math_algorithm 现在我运行main.py，报错：from math_algorithm.utils import parse_month_match_request，ModuleNotFoundError: No …...

编程日记 2024/6/1 11:27:47

go mod包管理与应用，常见错误排查方法

go mod包管理 go 中 包管理使用go mod 进行包管理 go mod init 项目名称 go mod init myproject_go生成的go.mod中有 module myproject_go 创建目录go_service 其下有两个go文件，go_request.go go_write.go . 根目录下有main.go入口文件。于是项目结构类似于&…...

编程日记 2024/6/1 11:26:46

数据结构作业

第1章 绪论 单选题 数据在计算机的存储器中表示时，逻辑上相邻的两个元素对应的物理地址也是相邻的，这种存储结构称之为________。 B. 顺序存储结构 算法指的是________。 D. 求解特定问题的指令有限序列 下面程序段的时间复杂度为：_______…...

编程日记 2024/6/1 11:24:43

项目纪实 | 版本升级操作get！GreatDB分布式升级过程详解

某客户项目现场，因其业务系统要用到数据库新版本中的功能特性，因此考虑升级现有数据库版本。在升级之前，万里数据库项目团队帮助客户在本地测试环境构造了相同的基础版本，导入部分生产数据，尽量复刻生产环境进行升级&a…...

编程日记 2024/6/1 11:18:36

富格林：应用正规技巧阻挠被骗

富格林悉知，随着如今入市现货黄金的朋友愈来愈多，不少投资者也慢慢开始重视起提高自身的正规投资技巧，希望能阻挠被骗更高效地在市场上获利。虽然目前黄金市场存在一定的受害风险，但只要投资者严格按照正规的交易规则来做单&#…...

编程日记 2024/6/1 11:16:34

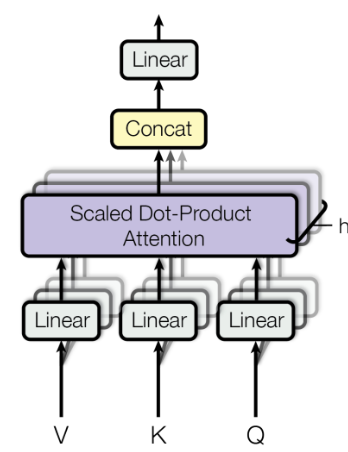
【模型架构】学习RNN、LSTM、TextCNN和Transformer以及PyTorch代码实现

一、前言 在自然语言处理（NLP）领域，模型架构的不断发展极大地推动了技术的进步。从早期的循环神经网络（RNN）到长短期记忆网络（LSTM）、Transformer再到当下火热的Mamba（放在下一节&a…...

编程日记 2024/6/1 11:15:32

【LeetCode】38.外观数列

外观数列 题目描述： 「外观数列」是一个数位字符串序列，由递归公式定义： countAndSay(1) "1"countAndSay(n) 是 countAndSay(n-1) 的行程长度编码。 行程长度编码（RLE）是一种字符串压缩方法&#xff0c…...

编程日记 2024/6/1 11:14:31

如何解决Ubuntu中软件包安装时的404错误(无法安装gdb、cgddb等)

目录 问题描述 解决方法 1. 更新软件包列表 2. 使用--fix-missing选项 3. 更换软件源 4. 清理和修复包管理器 总结 在使用Ubuntu进行软件包安装时，有时可能会遇到404错误。这种错误通常是由于软件源中的某些包已经被移除或迁移到其他位置。本文将介绍几种解决…...

编程日记 2024/6/1 11:13:30

SpringBoot中MyBatisPlus的使用

MyBatis Plus 是 MyBatis 的增强工具，提供了许多强大的功能，简化了 MyBatis 的使用。下面是在 Spring Boot 中使用 MyBatis Plus 的步骤： 添加依赖：在 Maven 或 Gradle 的配置文件中添加 MyBatis Plus 的依赖。 配置数据源&#…...

编程日记 2024/6/1 11:12:28

前后端交互：axios 和 json；springboot 和 vue

vue 准备的 <template><div><button click"sendData">发送数据</button><button click"getData">接收</button><button click"refresh">刷新</button><br><ul v-if"questions&…...

编程日记 2024/6/1 11:11:27

前端技术专家岗（虚拟岗）

定位&#xff1a; 团队技术负责人、技术领导者&#xff1b;确保框架、工具的低门槛、高性能、可扩展&#xff1b; 素质要求&#xff1a; 具备架构设计能力&#xff1b;一个或者多个领域的技术专家&#xff1b;较为丰富的基础建设经验&#xff1b;项目管理能力、任务分解、协…...

编程日记 2024/6/1 11:09:22

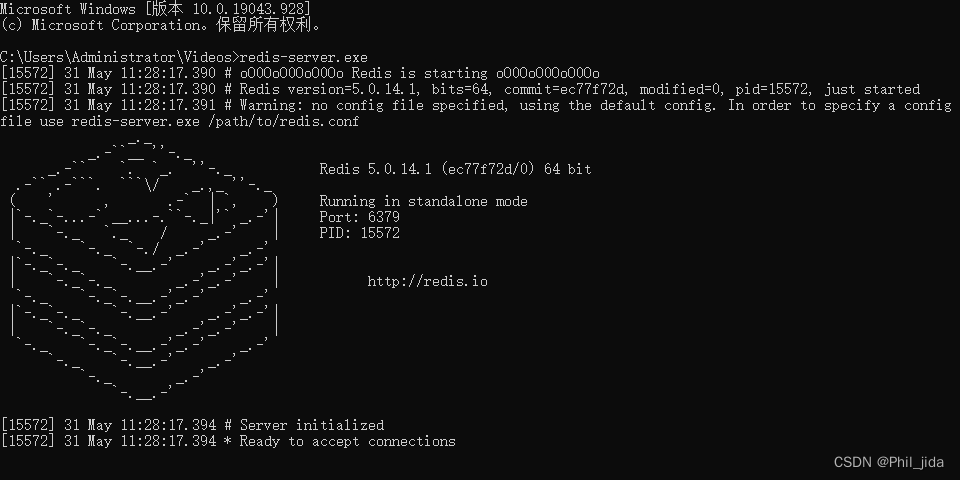
redis windows环境下的部署安装

2024Redis windows安装、部署与环境变量 一、下载 Redis官网目前暂不支持Windows版本&#xff0c;只能从github中下载。 windows 64位系统下载redis路径&#xff1a;https://github.com/tporadowski/redis/releases&#xff0c;下载zip包。 目前Windows版本只更新到5.0的版本…...

编程日记 2024/6/1 11:08:21

为内容生成应用动态切换 Taotoken 上的不同模型

&#x1f680; 告别海外账号与网络限制&#xff01;稳定直连全球优质大模型&#xff0c;限时半价接入中。 &#x1f449; 点击领取海量免费额度 为内容生成应用动态切换 Taotoken 上的不同模型 在内容创作类应用的开发中&#xff0c;一个常见的需求是根据不同的文本类型&#…...

编程新知 2026/5/16 10:49:21

生物信息学新手必看：用K-means和WGCNA分析转录组数据的保姆级流程（附R代码）

生物信息学实战&#xff1a;从K-means到WGCNA的转录组分析全流程指南 第一次接触转录组数据分析时&#xff0c;我盯着满屏的基因表达矩阵完全无从下手。那些论文里看似流畅的分析流程&#xff0c;在实际操作时却处处是坑——数据格式报错、参数设置不合理、结果解读模糊...这正…...

编程新知 2026/5/16 10:11:04

PyTorch实战：手写Sobel与Laplace算子实现图像边缘检测

1. 图像边缘检测与卷积算子基础 第一次接触图像处理时&#xff0c;我对"边缘检测"这个概念特别好奇。简单来说&#xff0c;边缘就是图像中物体轮廓或纹理变化明显的区域。想象一下用铅笔描边一幅画的过程&#xff0c;边缘检测就是让计算机自动完成这个工作。 为什么边…...

编程新知 2026/5/16 9:45:40

YOLOv8植物病害识别检测系统（项目源码+YOLO数据集+模型权重+UI界面+python+深度学习+环境配置）

摘要 植物病害是威胁全球农业产量与质量的主要因素之一&#xff0c;传统的人工识别方法依赖专家经验&#xff0c;效率低、主观性强。本文基于YOLOv8目标检测算法&#xff0c;构建了一套涵盖30类植物及其叶片病害的检测系统&#xff0c;包括苹果、玉米、马铃薯、番茄、葡萄等主…...

编程新知 2026/5/16 8:17:06

收藏！小白程序员轻松入门大模型：3个月实现转岗高薪offer的秘诀

本文针对传统程序员转行AI大模型的困境&#xff0c;提出三条实用路径&#xff1a;RAG应用工程、Agent应用开发、模型微调与部署。强调工程能力在AI应用中的重要性&#xff0c;建议通过解决实际问题积累经验&#xff0c;而非单纯堆砌技术栈。文章指出&#xff0c;懂业务、善工程…...

编程新知 2026/5/16 7:01:09

高性能计算终极指南：使用LIKWID工具套件进行性能分析与优化

高性能计算终极指南&#xff1a;使用LIKWID工具套件进行性能分析与优化 【免费下载链接】likwid Performance monitoring and benchmarking suite 项目地址: https://gitcode.com/gh_mirrors/li/likwid 在当今的高性能计算(HPC)领域&#xff0c;性能监控与分析是提升计算…...

编程新知 2026/5/16 4:42:09

Dot自定义配置指南：调整模型参数满足个性化需求

Dot自定义配置指南&#xff1a;调整模型参数满足个性化需求 【免费下载链接】Dot Text-To-Speech, RAG, and LLMs. All local! 项目地址: https://gitcode.com/gh_mirrors/dot1/Dot Dot是一款功能强大的本地AI应用&#xff0c;支持文本转语音、RAG&#xff08;检索增强生…...

编程新知 2026/5/16 4:27:31

苏峻：一个“产品偏执狂”的20年跨界史，从讲台到造车，他到底在疯什么？icar

苏峻&#xff1a;一个“产品偏执狂”的20年跨界史&#xff0c;从讲台到造车&#xff0c;他到底在疯什么&#xff1f;一个50岁的清华大学设计学博士&#xff0c;当过15年大学老师&#xff0c;做过空气净化器&#xff0c;卖过200万台&#xff0c;现在又跑去造车。有人说他是疯子&…...

编程新知 2026/5/16 4:21:20

Go语言策略模式：算法替换

Go语言策略模式&#xff1a;算法替换 1. 策略接口 type SortStrategy interface {Sort(data []int) []int }type BubbleSort struct{}func (s *BubbleSort) Sort(data []int) []int {// 冒泡排序实现return data }type QuickSort struct{}func (s *QuickSort) Sort(data []int)…...

编程新知 2026/5/16 3:05:38

科研绘图避坑指南：手把手教你用Cytoscape处理String PPI数据（TSV文件导入、节点筛选与双环图制作）

科研绘图避坑指南&#xff1a;Cytoscape实战PPI网络分析与双环图设计 在生物医学研究中&#xff0c;蛋白互作网络(PPI)可视化是揭示分子机制的重要工具。许多研究者在使用String数据库和Cytoscape软件时会遇到数据导入失败、节点筛选困难、图形美化耗时等问题。本文将针对这些痛…...

编程新知 2026/5/16 2:54:53