两整数之和 ---- 位运算
题目链接
题目:

分析:
- 题目中要求不能使用+-, 考虑到我们的位运算异或^, 是无进位加法, 可以使用
- 如果是无进位加法, 那么我们就要找到进位, 并进行计算, 进位只有1和1相加时才会产生进位1, 而0和1相加无进位, 进位为0, 那么我们就想到了&运算, 1&1 = 1, 0&1 = 0, 所以我们只需要将这两个数&, 就能知道有无进位
- 但是进位是给这一位的前一位加的, 所以我们要继续进行<<1 左移一位的操作
- 以示例二为例, 2的二进制是010, 3的二进制是011, 那么再进行^时, 结果是001, 进位就是100
- 接着就需要将进位和异或无进位相加后的结果相加, 还是使用异或运算, 无进位相加,那么结果就是101,结果为5
- 但是如果我们将进位和异或后的结果再进行异或后, 又产生了进位, 那么我们还要再进行&<<1的操作, 并和结果^ , 直到不再产生进位为止
代码:
class Solution {public int getSum(int a, int b) {while(b != 0){int x = a ^ b;int carry = (a & b) << 1;a = x;b = carry;}return a;}
}
相关文章:

两整数之和 ---- 位运算
题目链接 题目: 分析: 题目中要求不能使用-, 考虑到我们的位运算异或^, 是无进位加法, 可以使用如果是无进位加法, 那么我们就要找到进位, 并进行计算, 进位只有1和1相加时才会产生进位1, 而0和1相加无进位, 进位为0, 那么我们就想到了&运算, 1&1 1, 0&1 0, 所…...

长城电脑压缩文件丢失了怎么办?怎么解决
在数字化时代,电脑已成为我们日常生活和工作中不可或缺的设备。长城电脑作为国内知名品牌,以其稳定可靠的性能赢得了广大用户的信赖。然而,即便是可靠的电脑,也难免会遇到一些问题。其中,压缩文件丢失无疑是一个令人头…...

论文笔记《基于深度学习模型的药物-靶标结合亲和力预测》
基于深度学习模型的药物-靶标结合亲和力预测 这是一篇二区的文章,算是一个综述,记录一下在阅读过程中遇到的问题。 文章目录 基于深度学习模型的药物-靶标结合亲和力预测前言一、蛋白质接触图谱二、为什么蛋白质图谱的准确性对DTA模型预测结果没有影响1…...

ArrayList和LinkedList对比,ArrayList使用注意事项
ArrayList和LinkedList对比,ArrayList使用注意事项 ArrayList 和 LinkedList 是 Java 中常用的两种集合类,它们在内部实现和性能上有一些重要的区别。 ArrayList: ArrayList 是基于动态数组实现的。它内部使用一个数组来存储元素,当数组空间…...
小熊家务帮day5-day7 客户管理模块1 (小程序认证,手机验证码认证,账号密码认证,修改密码,找回密码等)
客户管理模块 1.认证模块1.1 认证方式介绍1.1.1 小程序认证1.1.2 手机验证码登录1.1.3 账号密码认证 1.2 小程序认证1.2.1 小程序申请1.2.2 创建客户后端工程jzo2o-customer1.2.3 开发部署前端1.2.4 小程序认证流程1.2.4.1 customer小程序认证接口设计Controller层Service层调用…...

计算机图形学入门02:线性代数基础
1.向量(Vetors) 向量表示一个方向,还能表示长度(向量的摸)。一般使用单位向量表示方向。 向量加减:平行四边形法则、三角形法则。比卡尔坐标系描述向量,坐标直接相加。 1.1向量点乘(…...
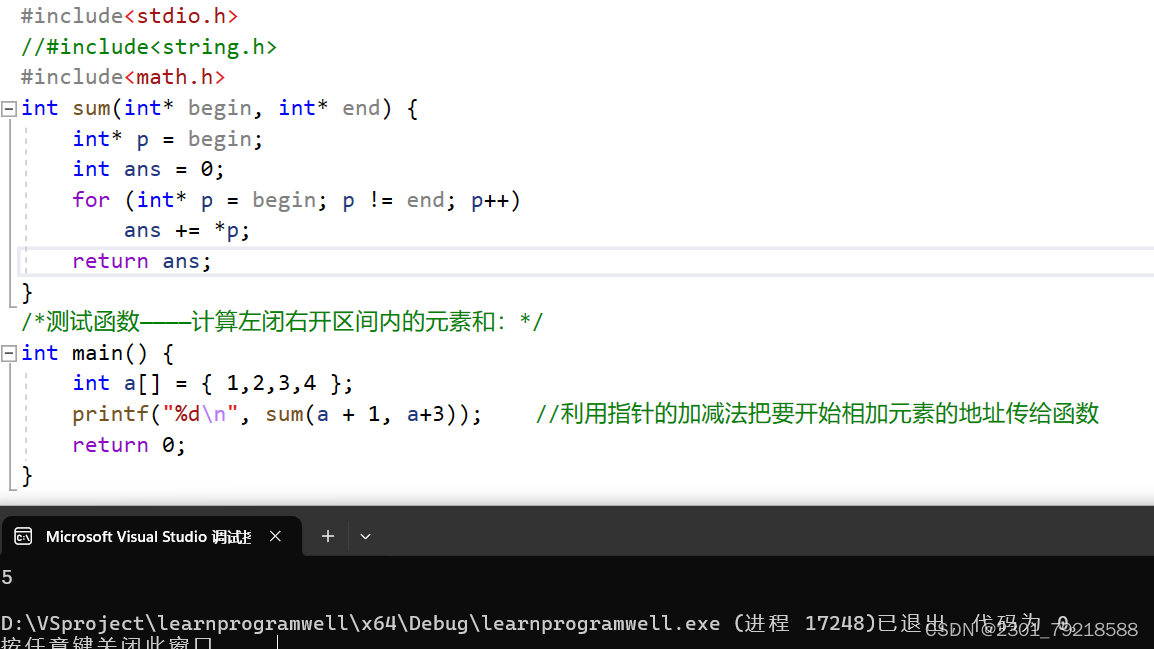
函数:计算数组的元素和
一、计算数组的元素和 参数传递给函数时,实际上只有数组的首地址作为指针传递给了函数。 在函数定义中的int a[ ]等价于int *a。在只有地址信息的情况下,是无法知道数组里有多少个元素的,因此在计算数组中的元素和时,要加一个参…...

如何进行数据库分库分表
当数据库的数据量增长到一定程度,单一数据库或表可能会遇到性能瓶颈,此时分库分表是一种常见的解决方案。以下是如何进行数据库分库分表的详细步骤和考虑因素,结合了参考文章中的相关信息: 一、分库分表概述 分库分表是为了解决…...
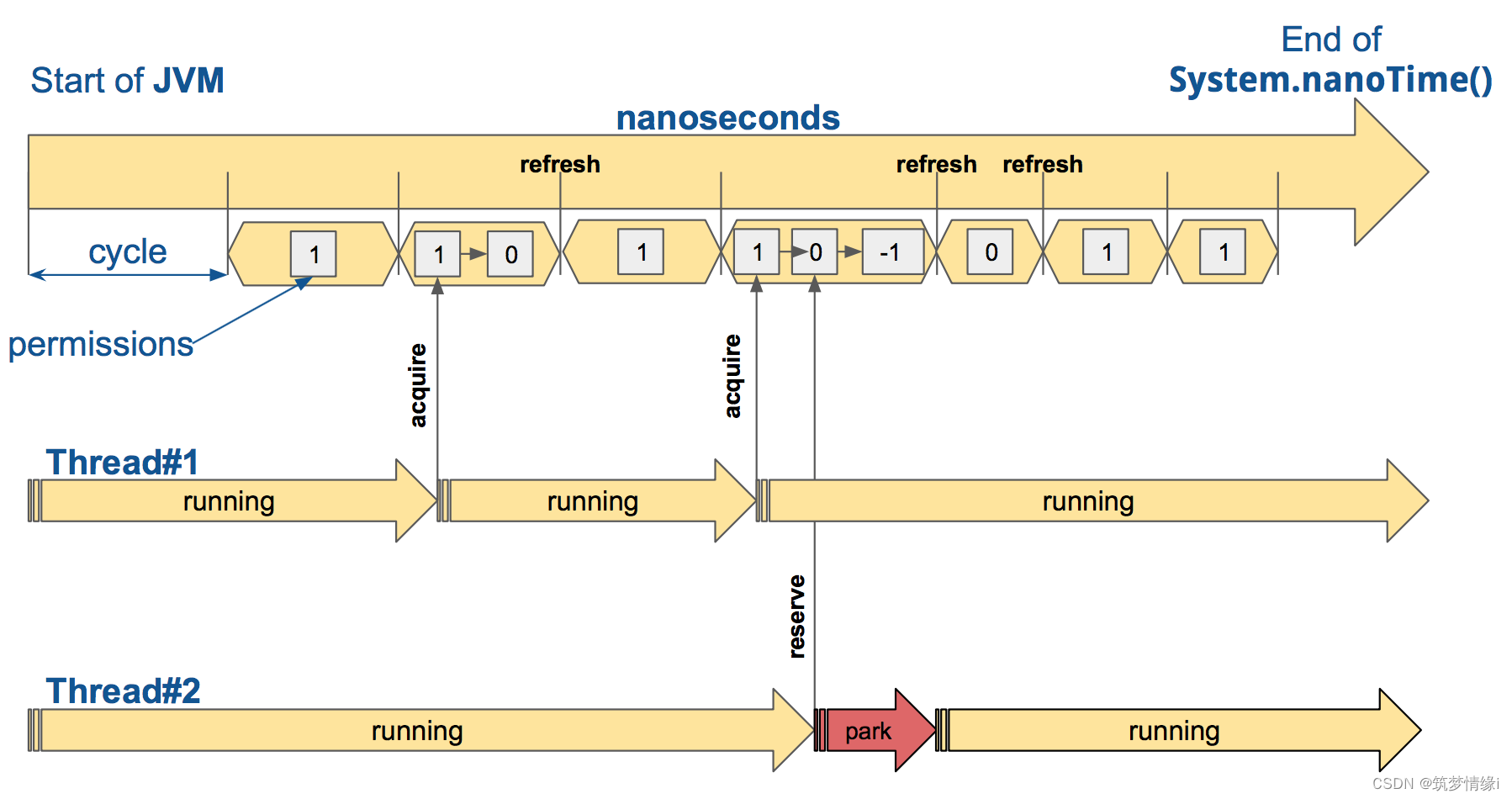
Spring-Cloud-CircuitBreaker-Resilience4j (3.1.1)
介绍 Resilience4j 是一个专为函数式编程而设计的轻量级容错库。Resilience4j 提供高阶函数(装饰器),以增强任何功能接口、lambda 表达式或方法引用,包括断路器、速率限制器、重试或隔板。您可以在任何函数接口、lambda 表达式或…...
)
重构与优化-组织数据(3)
重构组织数据是一个系统性的工程,旨在改进数据的存储方式、访问效率、质量和可用性,以更好地支持业务运营、分析决策和未来发展。以下是重构组织数据的一些关键说明点: 目的与动机 提升效率:通过优化数据结构、减少冗余数据和改善索引策略,加快数据查询和处理速度。 增强…...
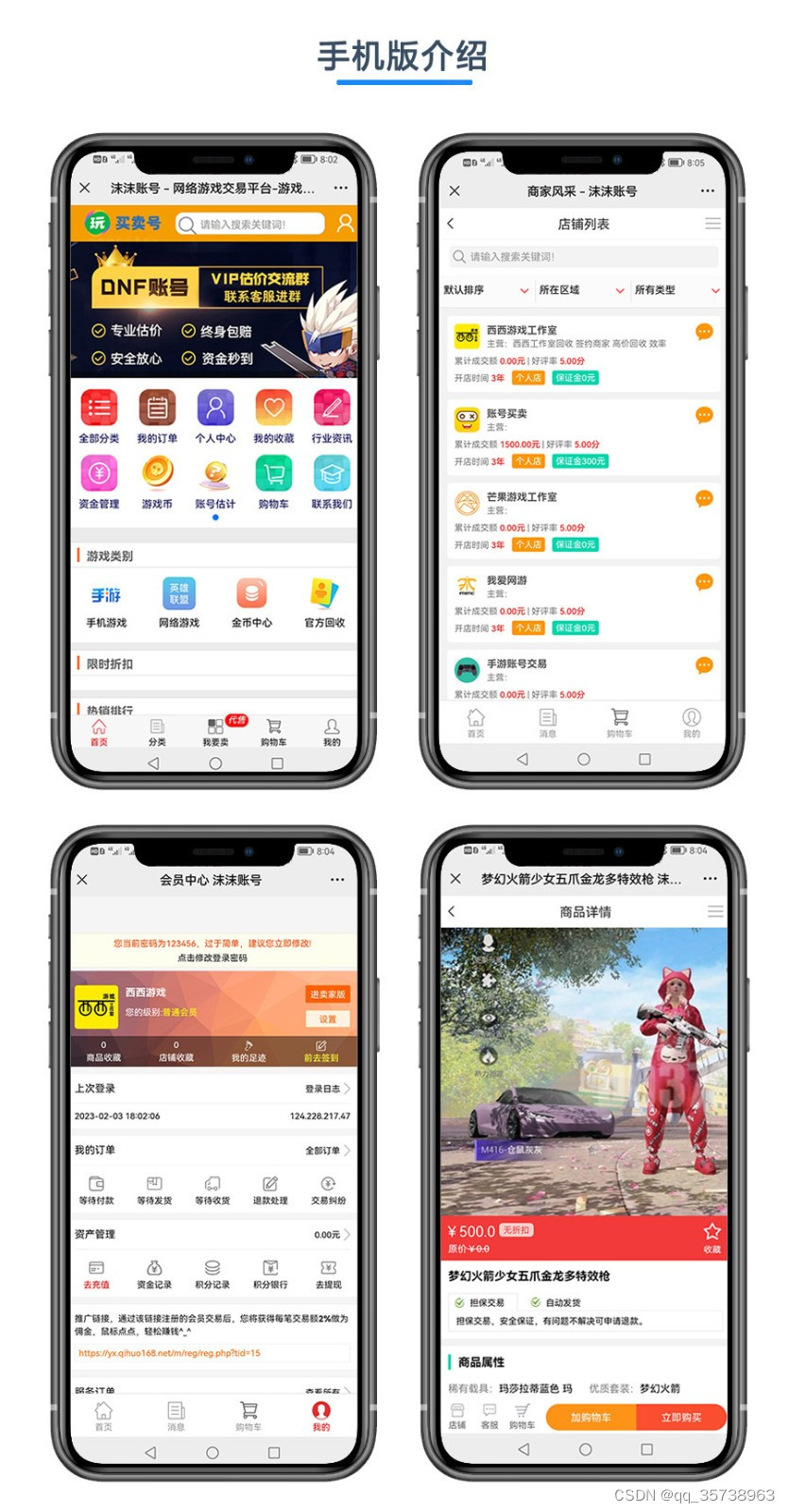
游戏交易平台源码游戏帐号交易平台系统源码
功能介绍 1:后台可以添加删除游戏分类 2:会员中心可以出售游戏币,账号,装备 3:后台可以对会员和商品进行管理 4:多商家入驻,商家发布信息 5:手机版功能可以生成APP 6:在线支付可支持微信和支…...

Matlab里面的浮点数与FPGA定点数的相互转化应用(含Matlab代码,封装成函数可直接调用)
微信公众号获取更多FPGA相关源码: 1.前言 Matlab里面计算通常用的是浮点数,而FPGA在做数字信号处理时,为了节约资源,常常使用的是定点数。在实践中,我们经常需要将Matlab实现中的算法,用FPGA进行实现。 …...

机器学习笔记——欠拟合、过拟合
欠拟合 将训练损失和测试损失都比较大的拟合叫欠拟合,那么他的预测精度很低 1.一般出现在模型的复杂度小于数据本身的复杂度导致的,这个可能就是模型对数据的分布和实际数据分布之间的差异,这个就可能需要更换模型 2.还可能出现在梯度下降算…...

【二进制部署k8s-1.29.4】七、验证master的安装
文章目录 简介 一.确认kubectl命令是否正常运行二.确认etcd安装是否正常运行三.确认kube-apiserver,kube-controller-manager,kube-scheduler安装是否正常四.配置apiserver和kubelet的访问授权五.master端安装脚本4.1.安装master端所需文件4.2.master快捷安装脚本 简介 本章节主…...

springboot获取当前数据库连接
要获取当前 Spring DataSource 的 URL,可以通过以下几种方法: 方法一:使用 JdbcTemplate 如果你使用的是 Spring 的 JdbcTemplate,可以通过 javax.sql.DataSource 获取连接,再获取它的 URL。 示例代码: …...
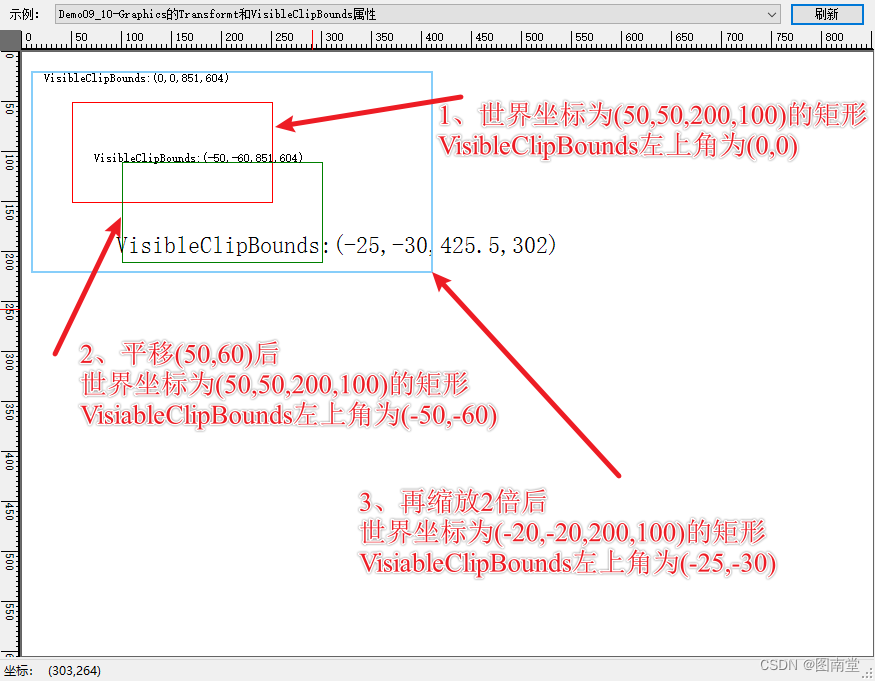
【学习笔记】Windows GDI绘图(九)Graphics详解(上)
文章目录 Graphics 定义创建Graphics对象的方法通过Graphics绘制不同的形状、线条、图像和文字等通过Graphics操作对象坐标 Graphics属性Clip(裁切/绘制区域)ClipBounds获取裁切区域矩形范围CompositiongMode合成方式CompositingQuality渲染质量DpiX和DpiY 水平、垂直分辨率Int…...

公告:公众号铁粉粉丝介绍以及说明
大家好,我是公众号博主--夏目 机械电气电机杂谈是我个人建立,为分享机械,电气,电机知识为主,闲谈杂聊社会时事,职场见闻,生活琐事,成长趣事,学习心得,读书观影…...

BioTech - 使用 CombFold 算法 实现 大型蛋白质复合物结构 的组装过程
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/139242199 CombFold 是用于预测大型蛋白质复合物结构的组合和分层组装算法,利用 AlphaFold2 预测的亚基之间的成对相互作用。 CombFold 算法的关键特点包括: 组合和…...

代码随想录算法训练营第36期DAY46
DAY46 完全背包 在闫氏DP法里学过:第i个物品选k个,纸质直至不能选,k从0开始取。就有递推式了。 代码随想录的视频也看了。 518零钱兑换ii 注意与 目标和 那题区分开。 完全背包问题,正向遍历背包容量,就能实现“多次…...

港湾周评|李小加“刀刃向内”裁员
《港湾商业观察》李镭 近年来争议颇大的滴灌通风波不断。 在交100万付费上班不久,最新又被曝出裁员。这位前港交所总裁、金融圈鼎鼎大名的李小加,没想到成立不足三年便迎来了重大挑战。 日前,滴灌通确认了公司组织架构已经调整,…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
