LabVIEW齿轮调制故障检测系统
LabVIEW齿轮调制故障检测系统
概述
开发了一种基于LabVIEW平台的齿轮调制故障检测系统,实现齿轮在恶劣工作条件下的故障振动信号的实时在线检测。系统利用LabVIEW的强大图形编程能力,结合Hilbert包络解调技术,对齿轮的振动信号进行精确分析,从而可靠地识别故障类型和位置。
齿轮作为机械传动系统中不可或缺的元件,其故障往往会导致整个机械系统的停工,带来巨大的经济损失。系统通过对齿轮振动信号的深入分析,实现故障的早期发现和准确诊断,进而有效地指导维护决策,减少非计划的停机时间。
系统组成与特点
硬件组成
数据采集卡:采用NI公司的PCI数据采集卡,因其高速的数据处理能力和广泛的兼容性,能够捕捉高频率的振动信号。
传感器:使用加速度传感器捕捉振动数据,其高灵敏度和精确性对于齿轮故障诊断至关重要。
软件架构
LabVIEW平台:作为系统开发的核心,提供了一套完整的信号处理VI库,简化了编程过程,并优化了数据处理流程。
Hilbert变换模块:专门用于信号的包络解调分析,是故障诊断中的关键技术。
特点
实时监控与分析:系统能够实现对齿轮状态的实时在线监控和分析,及时发现异常状态。
用户交互界面:提供直观的用户界面,包括实时数据显示、故障报警提示等功能,便于操作者监控和分析。
模块化设计:系统采用模块化设计,各功能模块独立,便于维护和升级。
工作原理
信号采集与处理
系统首先通过传感器收集齿轮的振动信号,然后通过数据采集卡将模拟信号转换为数字信号,输入到LabVIEW平台进行处理。信号处理流程包括时域分析、频域分析(FFT分析)和包络谱分析。
齿轮振动信号的特征分析
齿轮的振动信号主要反映了齿轮啮合的动态特性。正常情况下,振动信号主要由啮合频率及其相关谐波组成。一旦齿轮发生故障,如断齿、磨损等,振动信号便会出现异常的冲击和调制现象,这些现象在频谱中表现为调制边频带。
Hilbert解调分析
采用Hilbert变换对采集到的齿轮振动信号进行解调分析。通过这一技术,可以从调制的振动信号中提取关键的故障特征频率。解调后的信号表现为一系列的谐波和边带,通过分析这些频率成分的变化,可以准确地诊断出齿轮的具体故障位置和类型。
系统评估
通过与传统方法的对比,本系统显示出更高的故障识别准确率和更快的响应时间。通过实验验证,系统能够有效地识别和诊断各种齿轮故障,如断齿、磨损等,验证了其在工业应用中的可靠性和实用性。通过与传统方法的对比,本系统显示出更高的故障识别准确率和更快的响应时间。通过实验验证,系统能够有效地识别和诊断各种齿轮故障,如断齿、磨损等,验证了其在工业应用中的可靠性和实用性。

相关文章:

LabVIEW齿轮调制故障检测系统
LabVIEW齿轮调制故障检测系统 概述 开发了一种基于LabVIEW平台的齿轮调制故障检测系统,实现齿轮在恶劣工作条件下的故障振动信号的实时在线检测。系统利用LabVIEW的强大图形编程能力,结合Hilbert包络解调技术,对齿轮的振动信号进行精确分析…...

AI帮写:探索国内AI写作工具的创新与实用性
随着AI技术的快速发展,AI写作正成为创作的新风口。但是面对GPT-4这样的国际巨头,国内很多小伙伴往往望而却步,究其原因,就是它的使用门槛高,还有成本的考量。 不过,随着GPT技术的火热,国内也涌…...

n后问题 回溯笔记
问题描述 在nn格的棋盘上放置彼此不受攻击的n个皇后。 按照国际象棋的规则,皇后可以攻击与之处在同 一行或同一列或同一斜线上的棋子。n后问题等价于在nn格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。 代码 import java.uti…...

简述Java中实现Socket通信的步骤
在Java中,实现Socket通信通常涉及客户端和服务器端两个角色。以下是它们各自的基本步骤: 服务器端(Server) 创建ServerSocket对象: 在服务器端,首先需要创建一个ServerSocket对象。这个对象会监听来自客户…...
Asp.Net Core 实现分片下载的最简单方式
技术群里的朋友遇到了这个问题,起初的原因是他对文件增加了一个属性配置 fileResult.EnableRangeProcessing true;这个属性我从未遇到过,然后,去F1查看这个属性的描述信息也依然少的可怜,只有简单的描述为(获取或设置为 启用范围…...

[Mac软件]Leech for Mac v3.2 - 轻量级mac下载工具
黑果魏叔推荐Leech是由Many Tricks开发的适用于Mac OS X的轻量级且功能强大的下载管理器。 Leech让您完全控制下载,并与浏览器完全集成。您可以将下载排队,暂停和恢复,从受密码保护的服务器下载,并将密码存储在系统范围的安全钥匙…...
留给“端侧大模型”的时间不多了
端侧大模型(Edge AI models),也就是只在设备本地(如智能手机、IoT设备、嵌入式系统等)运行的大模型,过去一两年来非常流行。 具体表现在,终端设备厂商,如苹果、荣耀、小米、OV等&…...
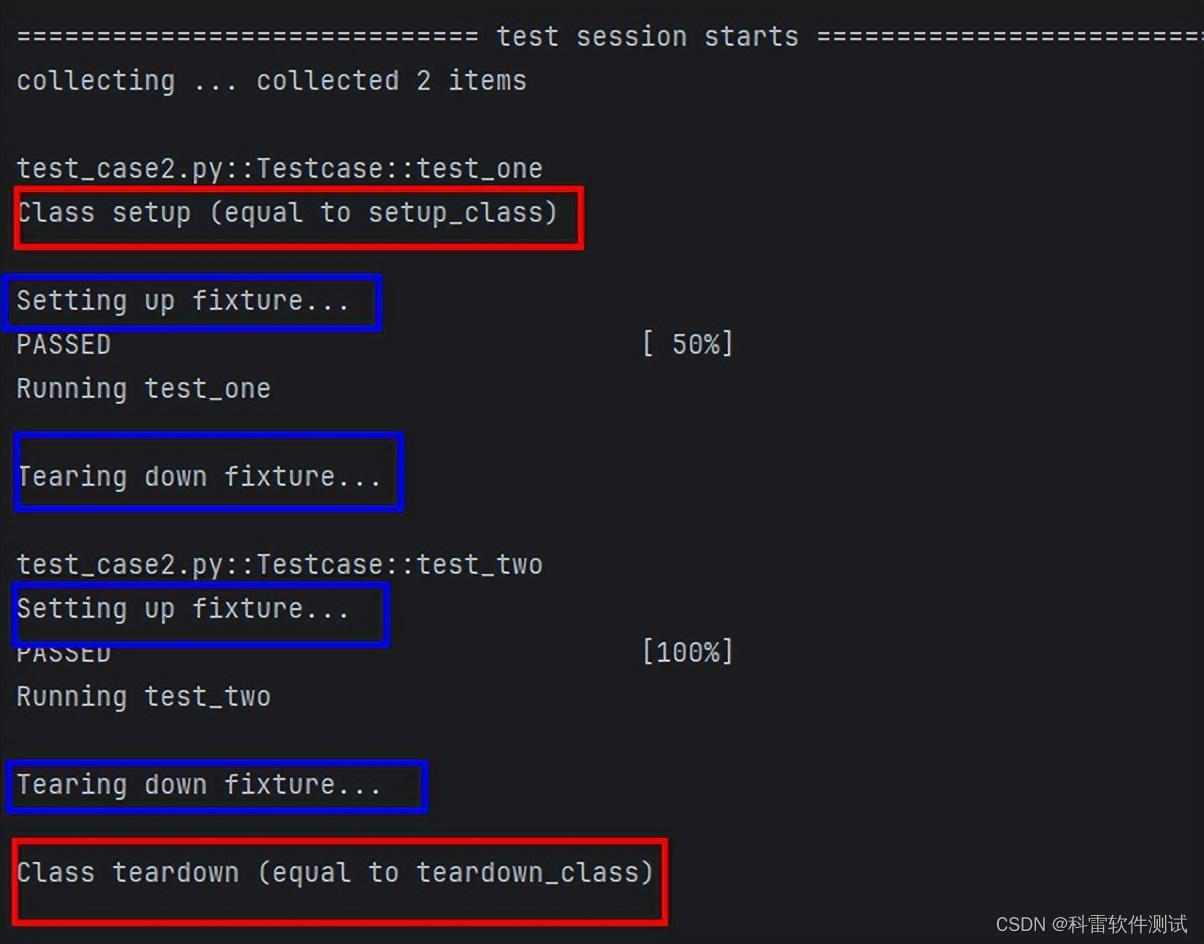
Pytest框架中的Setup和Teardown功能
在 pytest 测试框架中,setup 和 teardown是用于在每个测试函数之前和之后执行设置和清理的动作,而pytest 实际上并没有内置的 setup 和 teardown 函数,而是使用了一些装饰器或钩子函数来实现类似的功能。 学习目录 钩子函数(Hook…...

yolov10/v8 loss详解
v10出了就想看看它的loss设计有什么不同,看下来由于v8和v10的loss部分基本一致就放一起了。 v10的论文笔记,还没看的可以看看,初步尝试耗时确实有提升 好记性不如烂笔头,还是得记录一下,以免忘了,废话结束…...

Typescript高级: 深入理解infer关键字
概述 在 TS 中,infer 是一个高级类型操作,特别是条件类型和映射类型中非常有用的关键字它在泛型中使用也会是一个强大工具,增强了类型推断的能力,让开发者更灵活地处理和操作类型它允许在泛型类型推导过程中捕获一个具体的类型&a…...

JQC-3FF-S-Z 继电器模块使用(arduino)
前言 继电器模块可以控制电流的接通和非接通状态,和开关一样。实际上是用小电流去控制大电流运作的一种“自动开关” 本文只是简单使用继电器模块做一个 led 点亮和熄灭的案例,结合案例可以和 nodemcu 等板子结合做出远程控制开关。 材料准备 杜邦线…...
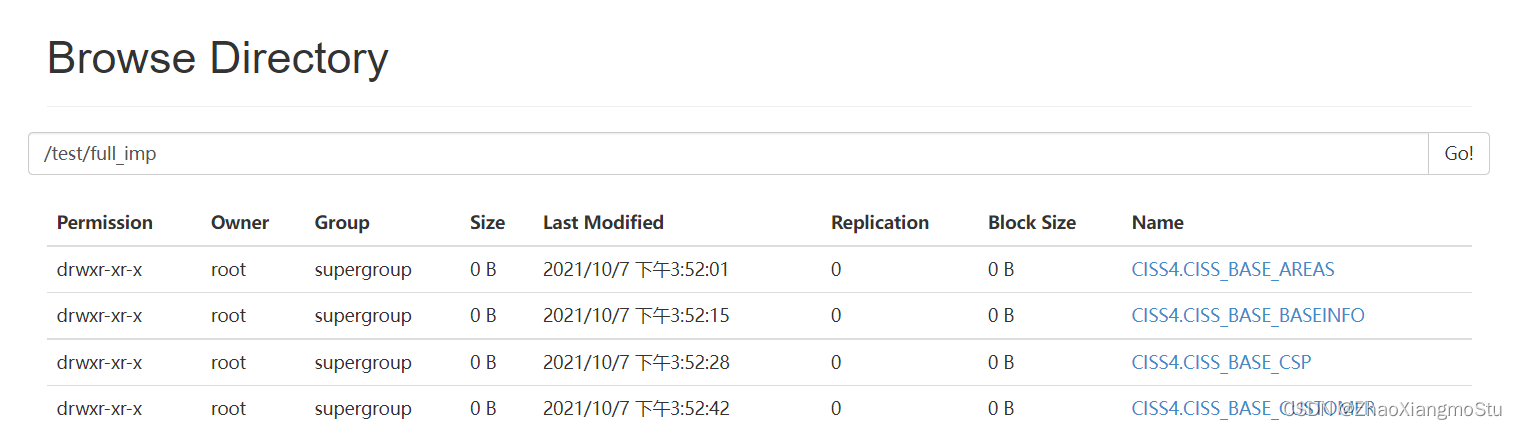
黑马一站制造数仓实战2
问题 DG连接问题 原理:JDBC:用Java代码连接数据库 Hive/SparkSQL:端口有区别 可以为同一个端口,只要不在同一台机器 项目:一台机器 HiveServer:10000 hiveserver.port 10000 SparkSQL:10001…...
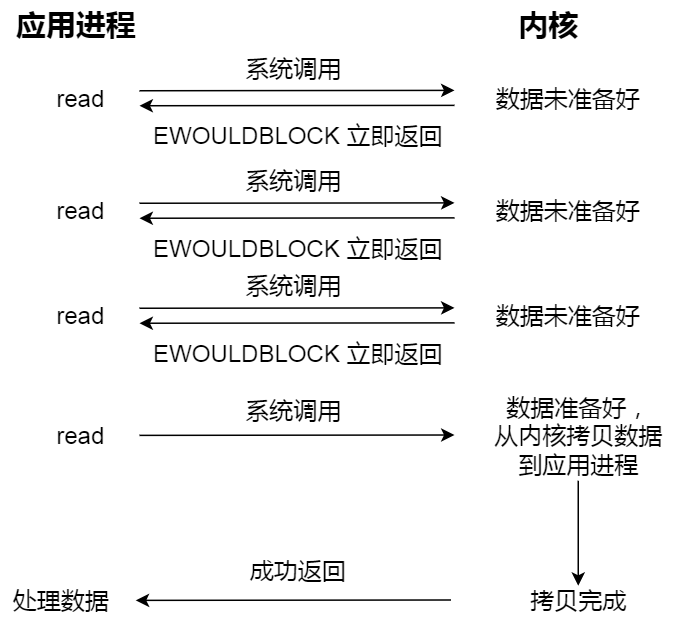
网络I/O模型
网络I/O模型 同步I/O阻塞I/O非阻塞I/OI/O多路复用select函数接口示例 poll函数接口示例 poll 和 select 的区别epoll原理:示例 异步I/O 同步I/O 阻塞I/O 一个基本的C/S模型如下图所图:其中 listen()、connect()、write()、read() 都是阻塞I/O࿰…...
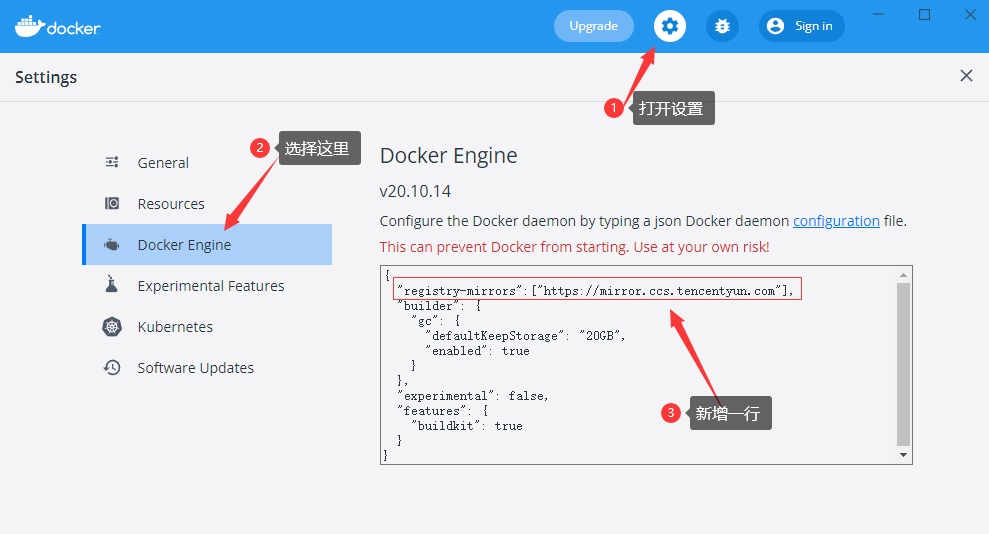
Docker 简介和安装
目录 Docker 是什么 跟普通虚拟机的对比 打包、分发、部署 Docker 部署的优势 Docker 通常用来做什么 重要概念:镜像、容器 安装 镜像加速源 Docker 是什么 Docker 是一个应用打包、分发、部署的工具 你也可以把它理解为一个轻量的虚拟机,它只虚…...

【源码】Spring Data JPA原理解析之Repository自定义方法命名规则执行原理(二)
Spring Data JPA系列 1、SpringBoot集成JPA及基本使用 2、Spring Data JPA Criteria查询、部分字段查询 3、Spring Data JPA数据批量插入、批量更新真的用对了吗 4、Spring Data JPA的一对一、LazyInitializationException异常、一对多、多对多操作 5、Spring Data JPA自定…...

Vue前端中从后端获取图片验证码
前端发送请求 <template><el-form :model"user" :rules"rules" ref"userForm" class"login" label-width"auto" style"max-width: 600px"><el-form-item label"用户名" prop"name…...
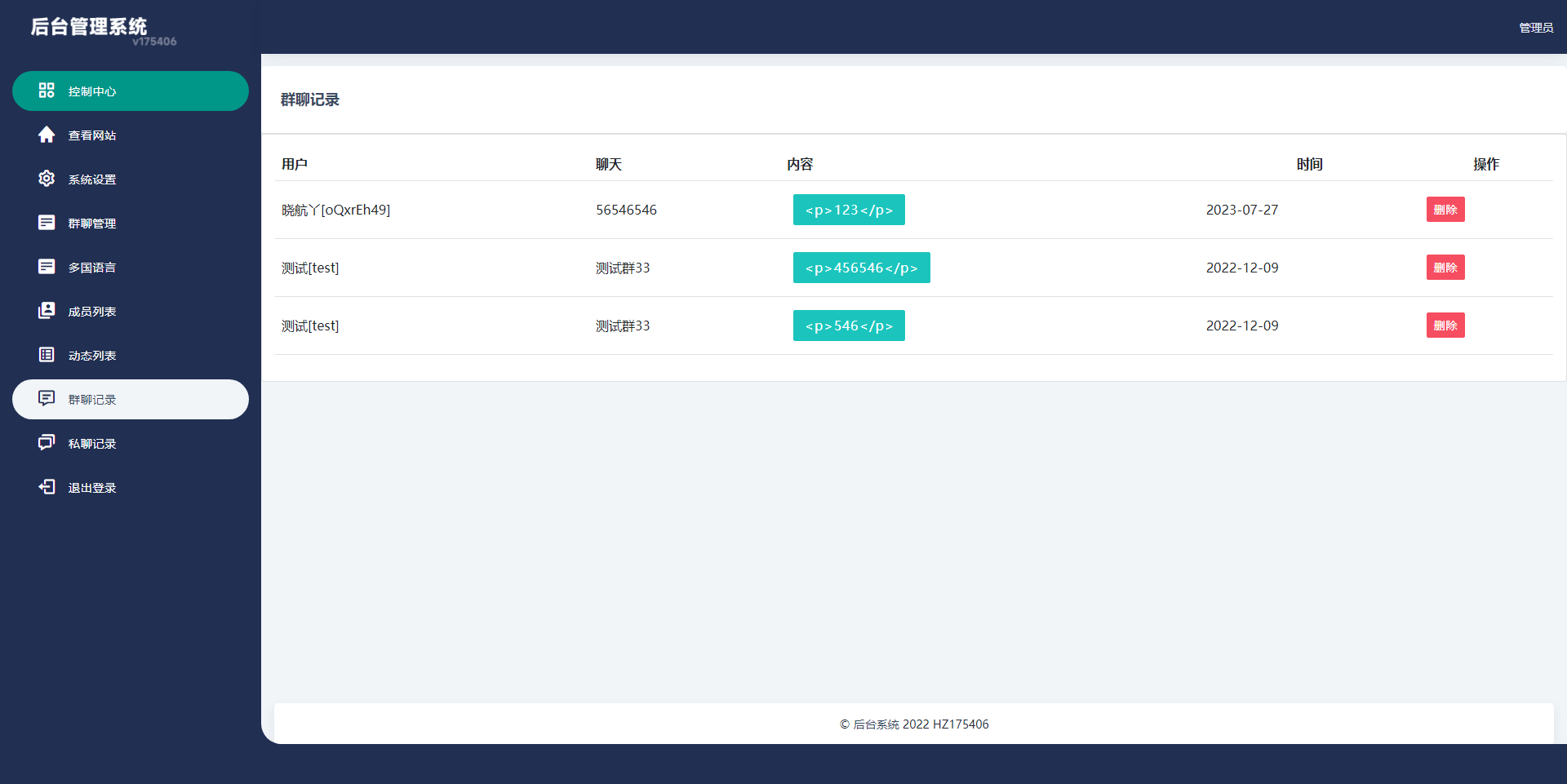
【源码】多语言H5聊天室/thinkphp多国语言即时通讯/H5聊天室源码/在线聊天/全开源
多语言聊天室系统,可当即时通讯用,系统默认无需注册即可进入群聊天,全开源 【海外聊天室】多语言H5聊天室/thinkphp多国语言即时通讯/H5聊天室源码/在线聊天/全开源 - 吾爱资源网...

gitlab 创建 ssh 和 token
文章目录 一、创建ssh key二、将密钥内容复制到gitlab三、创建token 一、创建ssh key 打开控制台cmd,执行命令 ssh-keygen -t rsa -C xxxxx xxxxx是你自己的邮箱 C:\Users\xx\.ssh 目录下会创建一个名为id_rsa.pub的文件,用记事本打开,并…...

Docker - Kafka
博文目录 文章目录 说明命令 说明 Docker Hub - bitnami/kafka Docker Hub - apache/kafka Kafka QuickStart Kafka 目前没有 Docker 官方镜像, 目前拉取次数最多的是 bitnami/kafka, Apache 提供的是 apache/kafka (更新最及时), 本文使用 bitnami/kafka bitnami/kafka 镜像…...
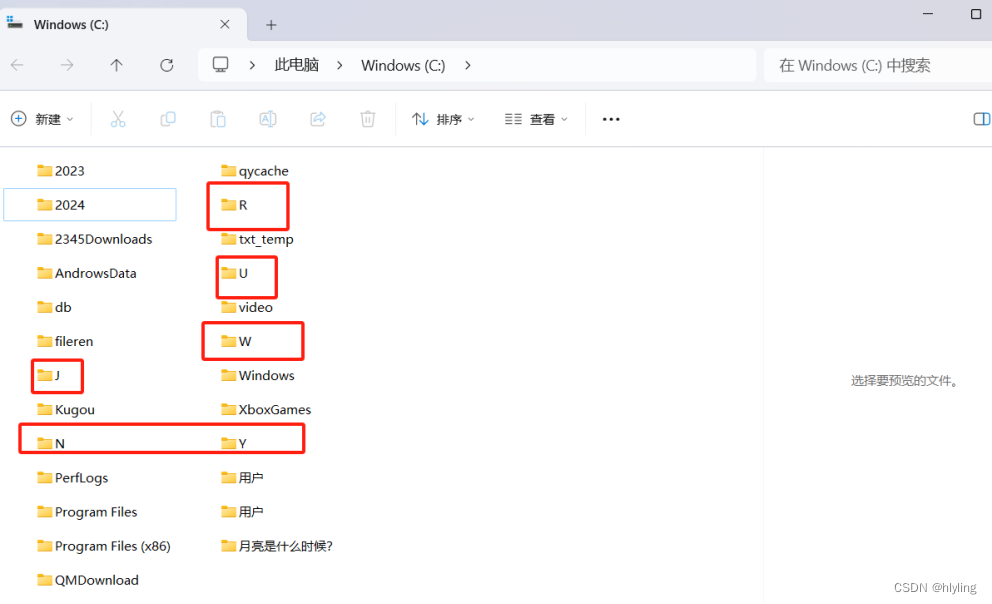
一键实现文件夹批量高效重命名:轻松运用随机一个字母命名,让文件管理焕然一新!
在数字化时代,文件夹管理是我们日常生活和工作中不可或缺的一部分。然而,随着文件数量的不断增加,文件夹命名的繁琐和重复成为了一个让人头疼的问题。你是否曾因为手动一个个重命名文件夹而感到枯燥乏味?你是否曾渴望有一种方法能…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...
