LeetCode 2965.找出缺失和重复的数字:小数据?我选择暴力(附优化方法清单:O(1)空间方法×3)
【LetMeFly】2965.找出缺失和重复的数字:小数据?我选择暴力(附优化方法清单:O(1)空间方法×3)
力扣题目链接:https://leetcode.cn/problems/find-missing-and-repeated-values/
给你一个下标从 0 开始的二维整数矩阵 grid,大小为 n * n ,其中的值在 [1, n2] 范围内。除了 a 出现 两次,b 缺失 之外,每个整数都 恰好出现一次 。
任务是找出重复的数字a 和缺失的数字 b 。
返回一个下标从 0 开始、长度为 2 的整数数组 ans ,其中 ans[0] 等于 a ,ans[1] 等于 b 。
示例 1:
输入:grid = [[1,3],[2,2]] 输出:[2,4] 解释:数字 2 重复,数字 4 缺失,所以答案是 [2,4] 。
示例 2:
输入:grid = [[9,1,7],[8,9,2],[3,4,6]] 输出:[9,5] 解释:数字 9 重复,数字 5 缺失,所以答案是 [9,5] 。
提示:
2 <= n == grid.length == grid[i].length <= 501 <= grid[i][j] <= n * n- 对于所有满足
1 <= x <= n * n的x,恰好存在一个x与矩阵中的任何成员都不相等。 - 对于所有满足
1 <= x <= n * n的x,恰好存在一个x与矩阵中的两个成员相等。 - 除上述的两个之外,对于所有满足
1 <= x <= n * n的x,都恰好存在一对i, j满足0 <= i, j <= n - 1且grid[i][j] == x。
解题方法:计数(模拟)
开辟一个 n 2 + 1 n^2+1 n2+1的数组,用来记录每个数分别出现了多少次。
遍历原始数组即可完成计数数组,遍历计数数组即可得到答案。
- 时间复杂度 O ( n 2 ) O(n^2) O(n2)
- 空间复杂度 O ( n 2 ) O(n^2) O(n2)
AC代码
C++
class Solution {
public:vector<int> findMissingAndRepeatedValues(vector<vector<int>>& grid) {vector<int> times(grid.size() * grid.size() + 1);for (vector<int>& line : grid) {for (int t : line) {times[t]++;}}vector<int> ans(2);for (int i = 1; i < times.size(); i++) {if (times[i] == 2) {ans[0] = i;}else if (times[i] == 0) {ans[1] = i;}}return ans;}
};
时间击败92.71%的提交,空间击败90.28%的提交。
其他方法
本题时间复杂度不可优化,说啥也得至少遍历一遍原始数组。如何优化空间复杂度呢?大致分为三种:
优化方法一:空间的原地使用:
例如 t t t出现过就将数组中第 t t t个元素置为负数,若某次将某元素置为负数时发现已经是负数了,则说明这个数出现了两次。到最后也没被置为负数的位置说明对应的数没有出现。
优化方法二:数学方法:
∑ i = 1 n 2 i − ∑ g r i d = b − a \sum_{i=1}^{n^2}i-\sum grid=b-a ∑i=1n2i−∑grid=b−a,一个方程不足以解出两个变量,因此可以再加一个方程。
例如 ∑ i = 1 n 2 i 2 − ∑ i ∈ g r i d i 2 = b 2 − a 2 \sum_{i=1}^{n^2}i^2-\sum_{i\in grid} i^2=b^2-a^2 ∑i=1n2i2−∑i∈gridi2=b2−a2,联立两方程即可得到 a a a和 b b b的值。
优化方法三:位运算:
根据异或的性质,异或一个数偶数次相当于没有异或。因此假设异或grid中的每个元素再异或从1到 n 2 n^2 n2得到结果 t t t,则 t = a ⊕ b t=a\oplus b t=a⊕b(相当于 a a a一共异或了3次而 b b b一共异或了1次)。
到这里很多同学都看出了这题本质和260. 只出现一次的数字 III相同。
如何拆分 a a a和 b b b?依据两个原则分别异或即可。假设 t t t二进制下第一个 1 1 1是第 2 2 2位,则所有数依据第 2 2 2位是否为 1 1 1分为两种。每组中所有元素相互异或,最终的两个结果就是 a a a和 b b b。
这里“所有数”是指 1 1 1到 n 2 n^2 n2的所有数以及原始数组中的所有数。
为什么这样能将 a a a和 b b b分开?因为根据异或结果 t t t可得, a a a和 b b b二进制下第 2 2 2位绝对不同,因此 a a a和 b b b会被分到两个不同的组中。每个组中除了 a a a或 b b b都出现偶数次,因此两组的异或结果就是 a a a和 b b b。
End
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/139357662
相关文章:
空间方法×3))
LeetCode 2965.找出缺失和重复的数字:小数据?我选择暴力(附优化方法清单:O(1)空间方法×3)
【LetMeFly】2965.找出缺失和重复的数字:小数据?我选择暴力(附优化方法清单:O(1)空间方法3) 力扣题目链接:https://leetcode.cn/problems/find-missing-and-repeated-values/ 给你一个下标从 0 开始的二维…...
)
【运维】VMware Workstation 虚拟机内无网络的解决办法(或许可行)
【使用桥接模式】 【重置网络】 这个过程涉及管理Linux系统中的网络驱动程序和网络管理工具。以下是每个步骤的详细解释: 卸载网络驱动模块: sudo rmmod e1000 sudo rmmod e1000e sudo rmmod igb这些命令使用 rmmod(remove moduleÿ…...
如何使用Dora SDK完成Fragment流式切换和非流式切换
我想大家对Fragment都不陌生,它作为界面碎片被使用在Activity中,如果只是更换Activity中的一小部分界面,是没有必要再重新打开一个新的Activity的。有时,即使要更换完整的UI布局,也可以使用Fragment来切换界面。 何…...
低代码开发平台(Low-code Development Platform)的模块组成部分
低代码开发平台(Low-code Development Platform)的模块组成部分主要包括以下几个方面: 低代码开发平台的模块组成部分可以按照包含系统、模块、菜单组织操作行为等维度进行详细阐述。以下是从这些方面对平台模块组成部分的说明: …...

Java网络编程(上)
White graces:个人主页 🙉专栏推荐:Java入门知识🙉 🙉 内容推荐:Java文件IO🙉 🐹今日诗词:来如春梦几多时?去似朝云无觅处🐹 ⛳️点赞 ☀️收藏⭐️关注💬卑微小博主&a…...

Spring Kafka 之 @KafkaListener 注解详解
我们在开发的过程中当使用到kafka监听消费的时候会使用到KafkaListener注解,下面我们就介绍下它的常见属性和使用。 一、介绍 KafkaListener 是 Spring Kafka 提供的一个注解,用于声明一个方法作为 Kafka 消息的监听器 二、主要参数 1、topic 描述&…...
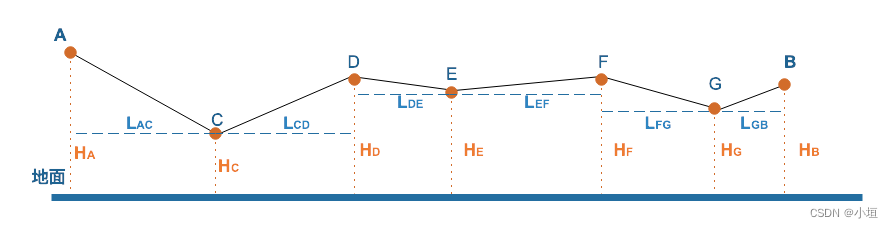
【量算分析工具-贴地距离】GeoServer改造Springboot番外系列九
【量算分析工具-概述】GeoServer改造Springboot番外系列三-CSDN博客 【量算分析工具-水平距离】GeoServer改造Springboot番外系列四-CSDN博客 【量算分析工具-水平面积】GeoServer改造Springboot番外系列五-CSDN博客 【量算分析工具-方位角】GeoServer改造Springboot番外系列…...
文件操作及vi)
【linux】(1)文件操作及vi
文件和目录的创建 创建文件 touch 命令:创建一个新的空文件。 touch filename.txtecho 命令:创建一个文件并写入内容。 echo "Hello, World!" > filename.txtcat 命令:将内容写入文件。 cat > filename.txt然后输入内容&…...
【5】MySQL数据库备份-XtraBackup - 全量备份
MySQL数据库备份-XtraBackup-全量备份 前言环境版本 安装部署下载RPM 包二进制包 安装卸载 场景分析全量备份 | 恢复备份恢复综合 增量备份 | 恢复部分备份 | 恢复 前言 关于数据库备份的一些常见术语、工具等,可见《MySQL数据库-备份》章节,当前不再重…...

数据治理-数据标准演示
数据字典 数据标准-数据字典 词根 数据标准-词根 业务字典映射 数据标准-业务字典映射 标准文档 数据标准-标准文档...
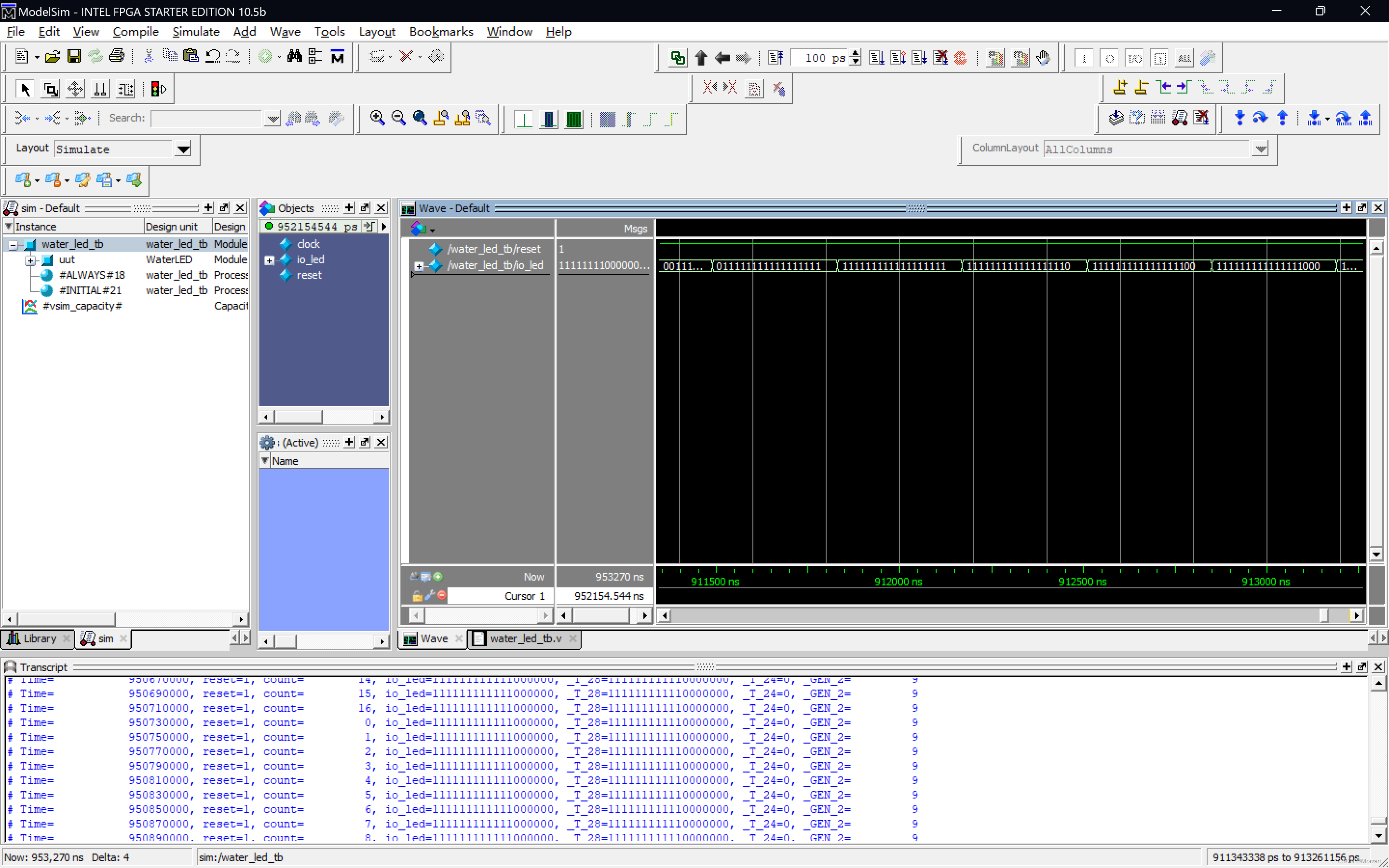
基于Chisel的FPGA流水灯设计
Chisel流水灯 一、Chisel(一)什么是Chisel(二)Chisel能做什么(三)Chisel的使用(四)Chisel的优缺点1.优点2.缺点 二、流水灯设计 一、Chisel (一)什么是Chise…...

LabVIEW齿轮调制故障检测系统
LabVIEW齿轮调制故障检测系统 概述 开发了一种基于LabVIEW平台的齿轮调制故障检测系统,实现齿轮在恶劣工作条件下的故障振动信号的实时在线检测。系统利用LabVIEW的强大图形编程能力,结合Hilbert包络解调技术,对齿轮的振动信号进行精确分析…...

AI帮写:探索国内AI写作工具的创新与实用性
随着AI技术的快速发展,AI写作正成为创作的新风口。但是面对GPT-4这样的国际巨头,国内很多小伙伴往往望而却步,究其原因,就是它的使用门槛高,还有成本的考量。 不过,随着GPT技术的火热,国内也涌…...

n后问题 回溯笔记
问题描述 在nn格的棋盘上放置彼此不受攻击的n个皇后。 按照国际象棋的规则,皇后可以攻击与之处在同 一行或同一列或同一斜线上的棋子。n后问题等价于在nn格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。 代码 import java.uti…...

简述Java中实现Socket通信的步骤
在Java中,实现Socket通信通常涉及客户端和服务器端两个角色。以下是它们各自的基本步骤: 服务器端(Server) 创建ServerSocket对象: 在服务器端,首先需要创建一个ServerSocket对象。这个对象会监听来自客户…...
Asp.Net Core 实现分片下载的最简单方式
技术群里的朋友遇到了这个问题,起初的原因是他对文件增加了一个属性配置 fileResult.EnableRangeProcessing true;这个属性我从未遇到过,然后,去F1查看这个属性的描述信息也依然少的可怜,只有简单的描述为(获取或设置为 启用范围…...

[Mac软件]Leech for Mac v3.2 - 轻量级mac下载工具
黑果魏叔推荐Leech是由Many Tricks开发的适用于Mac OS X的轻量级且功能强大的下载管理器。 Leech让您完全控制下载,并与浏览器完全集成。您可以将下载排队,暂停和恢复,从受密码保护的服务器下载,并将密码存储在系统范围的安全钥匙…...
留给“端侧大模型”的时间不多了
端侧大模型(Edge AI models),也就是只在设备本地(如智能手机、IoT设备、嵌入式系统等)运行的大模型,过去一两年来非常流行。 具体表现在,终端设备厂商,如苹果、荣耀、小米、OV等&…...
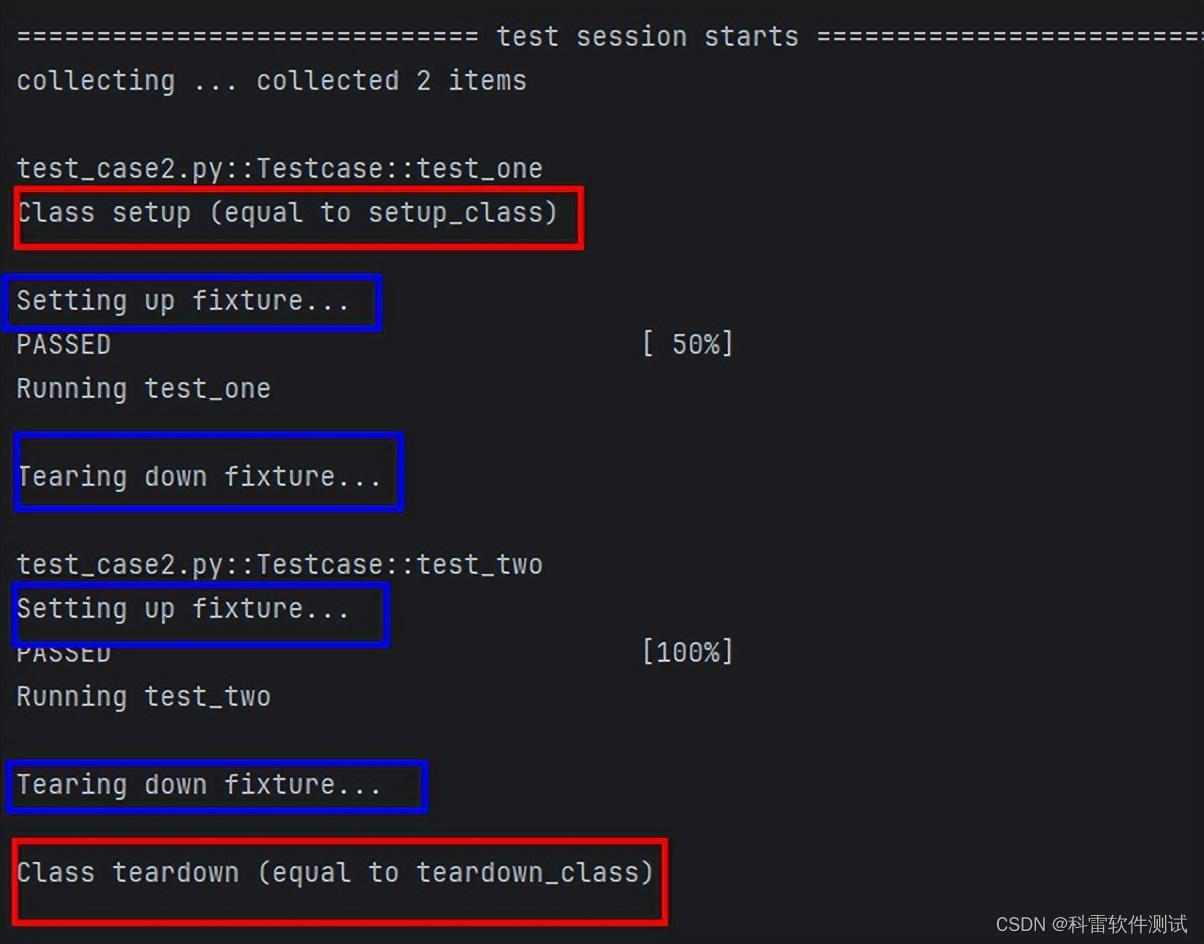
Pytest框架中的Setup和Teardown功能
在 pytest 测试框架中,setup 和 teardown是用于在每个测试函数之前和之后执行设置和清理的动作,而pytest 实际上并没有内置的 setup 和 teardown 函数,而是使用了一些装饰器或钩子函数来实现类似的功能。 学习目录 钩子函数(Hook…...

yolov10/v8 loss详解
v10出了就想看看它的loss设计有什么不同,看下来由于v8和v10的loss部分基本一致就放一起了。 v10的论文笔记,还没看的可以看看,初步尝试耗时确实有提升 好记性不如烂笔头,还是得记录一下,以免忘了,废话结束…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
