JVM常用概念之锁粗化和循环
1.什么是锁粗化
锁粗化一般指有效地合并几个相邻的锁定块,从而减少锁定开销。如下述代码所示:
锁粗化前代码:
synchronized (obj) {// statements 1
}
synchronized (obj) {// statements 2
}
锁粗化后代码:
synchronized (obj) {// statements 1// statements 2
}
2.循环场景下的锁粗化
循环场景下的锁粗化一般指合并几个循环体内的锁定块,如下述代码所示:
锁粗化前:
for (...) {synchronized (obj) {// something}
}
锁粗化后:
synchronized (this) {for (...) {// something}
}
3.锁粗化可能带来的问题
使锁变得过于粗化,以至于特定线程在执行循环时会独占锁,从而导致大量线程阻塞。
相关文章:

JVM常用概念之锁粗化和循环
1.什么是锁粗化 锁粗化一般指有效地合并几个相邻的锁定块,从而减少锁定开销。如下述代码所示: 锁粗化前代码: synchronized (obj) {// statements 1 } synchronized (obj) {// statements 2 }锁粗化后代码: synchronized (obj)…...
)
HTML (总结黑马的)
<br>换行 <hr>水平线 div 独占一行 span 不换行 header 网页头部 nav 网页导航 footer 网页底部 aside 网页侧边栏 section 网页区块 article 网页文章 空格 < 小于号 > 大于号 图片: <img src"./cat.jpg" alt&q…...

YOLOv8 segment介绍
1.YOLOv8图像分割支持的数据格式: (1).用于训练YOLOv8分割模型的数据集标签格式如下: 1).每幅图像对应一个文本文件:数据集中的每幅图像都有一个与图像文件同名的对应文本文件,扩展名为".txt"; 2).文本文件中每个目标(object)占一行…...

PMBOK® 第六版 项目整合管理概念
目录 读后感—PMBOK第六版 目录 项目往往会牵涉到众多专业的知识以及来自不同专业、具有不同性格且可能处在不同地理位置的人员,存在着诸多不同分工的状况。要是没有统一的目标,相互之间也没有有效的沟通机制,并且不存在计划、监控以及平衡等…...

【Qt】【模型视图架构】代理模型
文章目录 代理模型简单介绍QSortFilterProxyModel类简单介绍排序过滤子类化 代理模型简单介绍 代理模型的作用是可以将一个模型中的数据进行排序或者过滤,然后提供给视图进行显示。 如下所示,创建一个源模型、一个代理模型,界面上创建一个列…...
Flutter 中的 IconTheme 小部件:全面指南
Flutter 中的 IconTheme 小部件:全面指南 Flutter 是一个功能丰富的 UI 开发框架,它允许开发者使用 Dart 语言来构建跨平台的移动、Web 和桌面应用。在 Flutter 的丰富组件库中,IconTheme 是一个用于设置应用中图标主题的小部件,…...

virtualbox虚拟机、centos7安装增强工具
文章目录 1. virtualBox语言设置2. 设置终端启动快捷键3. 添加virtualbox 增强工具4. 设置共享文件夹 1. virtualBox语言设置 virtualbox -> file -> perferences -> language ->选择对应的语言 -> OK virtualbox -> 管理 -> 全局设定 -> 语言 -> …...

Kotlin 泛型
文章目录 定义泛型属性泛型函数泛型类或接口 where 声明多个约束泛型具体化in、out 限制泛型输入输出 定义 有时候我们会有这样的需求:一个类可以操作某一类型的对象,并且限定只有该类型的参数才能执行相关的操作。 如果我们直接指定该类型Intÿ…...
)
Tomcat 面试题(一)
1. 简述什么是Tomcat ? Tomcat是一个开源的Java Servlet容器,它实现了Java Servlet和JavaServer Pages (JSP)技术,提供了一个运行Java Web应用程序的平台。Tomcat由Apache软件基金会维护,并广泛用于开发和部署Web应用程序。 Tom…...

跟踪一个Pytorch Module在训练过程中的内存分配情况
跟踪一个Pytorch Module在训练过程中的内存分配情况 代码输出 目的:跟踪一个Pytorch Module在训练过程中的内存分配情况 方法: 1.通过pre_hook module的来区分module的边界 2.通过__torch_dispatch__拦截所有的aten算子,计算在该算子中新创建tensor的总内存占用量 3.通过tensor…...
空间方法×3))
LeetCode 2965.找出缺失和重复的数字:小数据?我选择暴力(附优化方法清单:O(1)空间方法×3)
【LetMeFly】2965.找出缺失和重复的数字:小数据?我选择暴力(附优化方法清单:O(1)空间方法3) 力扣题目链接:https://leetcode.cn/problems/find-missing-and-repeated-values/ 给你一个下标从 0 开始的二维…...
)
【运维】VMware Workstation 虚拟机内无网络的解决办法(或许可行)
【使用桥接模式】 【重置网络】 这个过程涉及管理Linux系统中的网络驱动程序和网络管理工具。以下是每个步骤的详细解释: 卸载网络驱动模块: sudo rmmod e1000 sudo rmmod e1000e sudo rmmod igb这些命令使用 rmmod(remove moduleÿ…...
如何使用Dora SDK完成Fragment流式切换和非流式切换
我想大家对Fragment都不陌生,它作为界面碎片被使用在Activity中,如果只是更换Activity中的一小部分界面,是没有必要再重新打开一个新的Activity的。有时,即使要更换完整的UI布局,也可以使用Fragment来切换界面。 何…...
低代码开发平台(Low-code Development Platform)的模块组成部分
低代码开发平台(Low-code Development Platform)的模块组成部分主要包括以下几个方面: 低代码开发平台的模块组成部分可以按照包含系统、模块、菜单组织操作行为等维度进行详细阐述。以下是从这些方面对平台模块组成部分的说明: …...

Java网络编程(上)
White graces:个人主页 🙉专栏推荐:Java入门知识🙉 🙉 内容推荐:Java文件IO🙉 🐹今日诗词:来如春梦几多时?去似朝云无觅处🐹 ⛳️点赞 ☀️收藏⭐️关注💬卑微小博主&a…...

Spring Kafka 之 @KafkaListener 注解详解
我们在开发的过程中当使用到kafka监听消费的时候会使用到KafkaListener注解,下面我们就介绍下它的常见属性和使用。 一、介绍 KafkaListener 是 Spring Kafka 提供的一个注解,用于声明一个方法作为 Kafka 消息的监听器 二、主要参数 1、topic 描述&…...
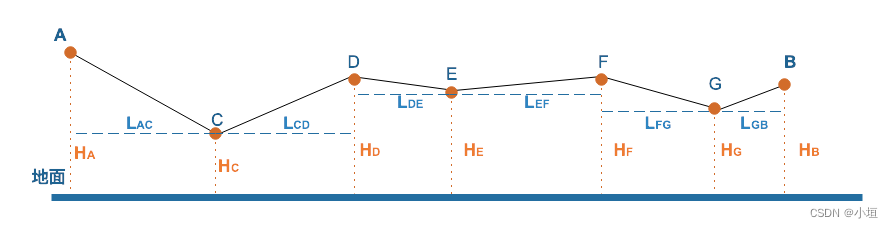
【量算分析工具-贴地距离】GeoServer改造Springboot番外系列九
【量算分析工具-概述】GeoServer改造Springboot番外系列三-CSDN博客 【量算分析工具-水平距离】GeoServer改造Springboot番外系列四-CSDN博客 【量算分析工具-水平面积】GeoServer改造Springboot番外系列五-CSDN博客 【量算分析工具-方位角】GeoServer改造Springboot番外系列…...
文件操作及vi)
【linux】(1)文件操作及vi
文件和目录的创建 创建文件 touch 命令:创建一个新的空文件。 touch filename.txtecho 命令:创建一个文件并写入内容。 echo "Hello, World!" > filename.txtcat 命令:将内容写入文件。 cat > filename.txt然后输入内容&…...
【5】MySQL数据库备份-XtraBackup - 全量备份
MySQL数据库备份-XtraBackup-全量备份 前言环境版本 安装部署下载RPM 包二进制包 安装卸载 场景分析全量备份 | 恢复备份恢复综合 增量备份 | 恢复部分备份 | 恢复 前言 关于数据库备份的一些常见术语、工具等,可见《MySQL数据库-备份》章节,当前不再重…...

数据治理-数据标准演示
数据字典 数据标准-数据字典 词根 数据标准-词根 业务字典映射 数据标准-业务字典映射 标准文档 数据标准-标准文档...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
