transfomer中attention为什么要除以根号d_k
简介
得到矩阵 Q, K, V之后就可以计算出 Self-Attention 的输出了,计算的公式如下:
A t t e n t i o n ( Q , K , V ) = S o f t m a x ( Q K T d k ) V Attention(Q,K,V)=Softmax(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=Softmax(dkQKT)V
好处
除以维度的开方,可以将数据向0方向集中,使得经过softmax后的梯度更大.
从数学上分析,可以使得QK的分布和Q/K保持一致,
推导
对于两个独立的正态分布而言,两者的加法的期望和方差就是两个独立分布的期望和方差。
qk_T的计算过程为[len_q,dim][dim,len_k]=[len_q,len_k],qk的元素等于dim个乘积的和。对于0-1分布表乘积不会影响期望和方差,但是求和操作会使得方差乘以dim,因此对qk元素除以sqrt(dim)把标准差压回1.
这里展示一个不严谨的采样可视化过程
假设在query在(0,1)分布,key在(0,1)分布,随机采样lengthdim个点,然后统计querykey_T的散点的分布
import math
import numpy as np
import matplotlib.pyplot as pltdef plot_curve(mu=0, sigma =1):import numpy as npimport matplotlib.pyplot as pltfrom scipy.stats import norm# 设置正态分布的参数# mu, sigma = 0, 1 # 均值和标准差# 创建一个x值的范围,覆盖正态分布的整个区间x = np.linspace(mu - 4 * sigma, mu + 4 * sigma, 1000)# 计算对应的正态分布的概率密度值y = norm.pdf(x, mu, sigma)# 我们可以选择y值较高的点来绘制散点图,以模拟概率密度的分布# 这里我们可以设置一个阈值,只绘制y值大于某个值的点threshold = 0.01 # 可以根据需要调整这个阈值selected_points = y > thresholdplt.plot(x, y, 'r-', lw=2, label='Normal dist. (mu={}, sigma={})'.format(mu, sigma))plt.title('Normal Distribution Scatter Approximation')plt.xlabel('Value')plt.ylabel('Probability Density')plt.legend()plt.grid(True)plt.show()def plot_poins(x):# 因为这是一个一维的正态分布,我们通常只绘制x轴上的点# 但为了模拟二维散点图,我们可以简单地将y轴设置为与x轴相同或固定值(例如0)y = np.zeros_like(x)# 绘制散点图plt.figure(figsize=(8, 6))plt.scatter(x, y, alpha=0.5) # alpha控制点的透明度plt.title('Normal (0, 1) Distribution Scatter Plot')plt.xlabel('Value')plt.ylabel('Value (or Frequency if binned)')plt.grid(True)plt.show()if __name__ == '__main__':# 设置随机种子以便结果可复现np.random.seed(0)len = 10000dim = 100query = np.random.normal(0, 1, len*dim).reshape(len,dim)key = np.random.normal(0, 1, len*dim).reshape(dim,len)qk = np.matmul(query,key) / math.sqrt(dim)mean_query = query.mean()std_query = np.std(query,ddof=1)mean_key = key.mean()std_key = np.std(key,ddof=1)mean_qk = qk.mean()std_qk = np.std(qk,ddof=1)plot_poins(query)plot_curve(mean_query,std_query)

相关文章:

transfomer中attention为什么要除以根号d_k
简介 得到矩阵 Q, K, V之后就可以计算出 Self-Attention 的输出了,计算的公式如下: A t t e n t i o n ( Q , K , V ) S o f t m a x ( Q K T d k ) V Attention(Q,K,V)Softmax(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)Softmax(dk QKT)V 好处 除以维…...
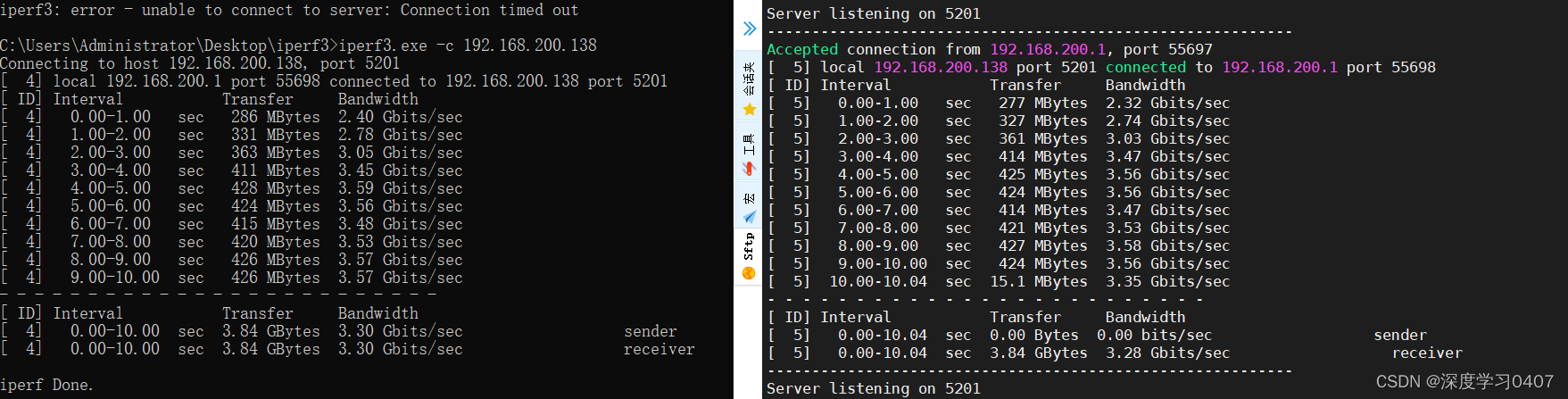
iperf3带宽压测工具使用
iperf3带宽压测工具使用 安装下载地址:[下载入口](https://iperf.fr/iperf-download.php)测试结果:时长测试(压测使用):并行测试反向测试UDP 带宽测试 iPerf3 是用于主动测试 IP 网络上最大可用带宽的工具 安装 下载地址&#x…...

[数据集][目标检测]焊接处缺陷检测数据集VOC+YOLO格式3400张8类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):3400 标注数量(xml文件个数):3400 标注数量(txt文件个数):3400 标注…...
)
2024华为OD机试真题-剩余银饰的重量-C++(C卷D卷)
题目描述 有 N 块二手市场收集的银饰,每块银饰的重量都是正整数,收集到的银饰会被熔化用于打造新的饰品。 每一回合,从中选出三块 最重的 银饰,然后一起熔掉。假设银饰的重量分别为 x 、y 和 z, 且 x <= y <= z。那么熔掉的可能结果如下: 如果x == y == z,那么三…...

糖果促销【百度之星】/思维
糖果促销 思维 大佬的解法: #include<bits/stdc.h> using namespace std; typedef long long ll; int main() {ll t;cin>>t;for(int i0;i<t;i){ll p,k;cin>>p>>k;if(k0) cout<<0<<endl;else{k-(k-1)/p;cout<<k<…...
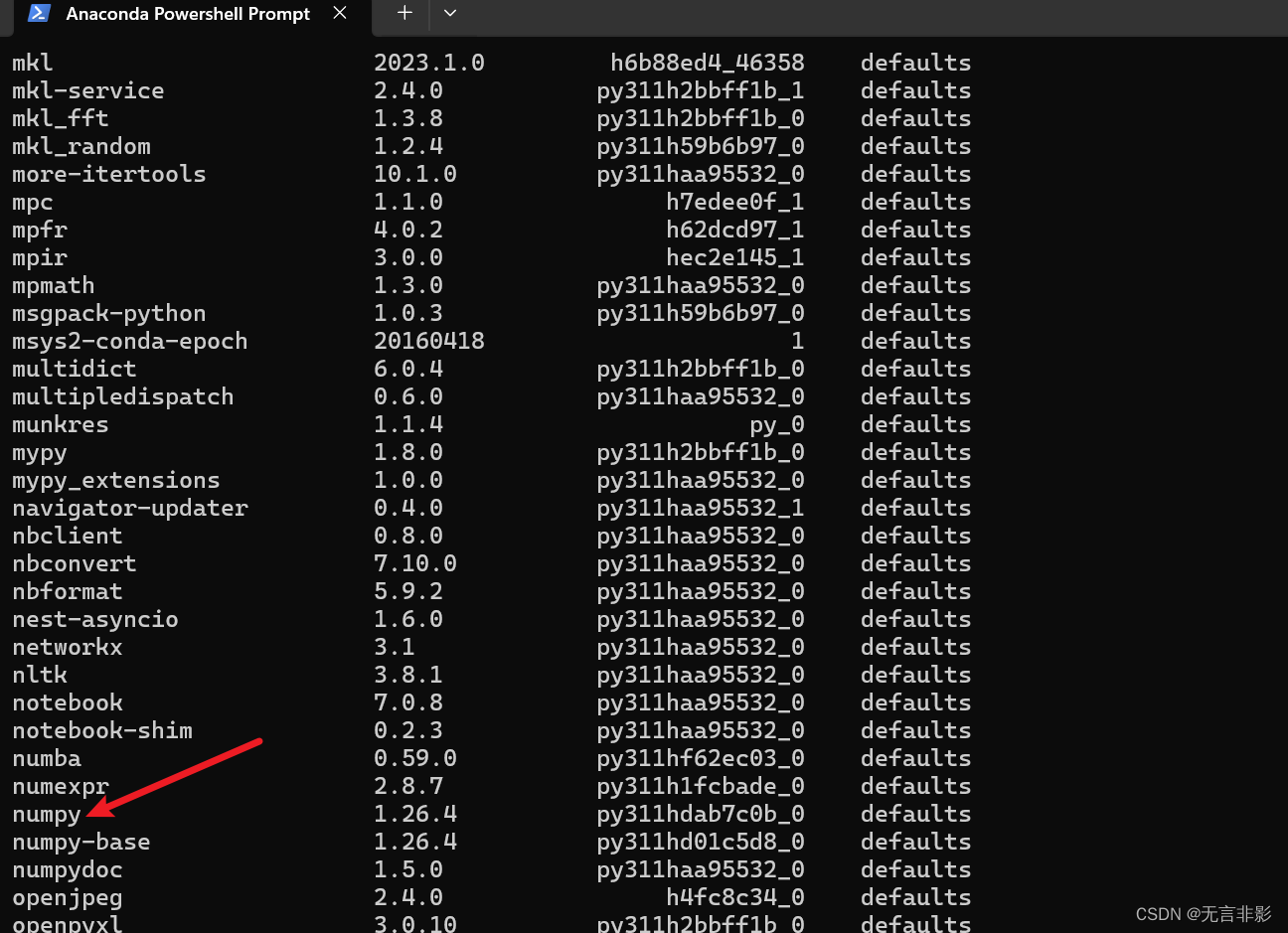
【python学习】安装Anaconda后,如何进行环境管理(命令行操作及图形化操作Anaconda Navigator)及包管理
命令行的方式 首先,打开 Anaconda Powershell Prompt 环境查看 使用以下命令查看当前所有环境: conda env list目前只有一个 base环境,就是安装 anaconda的时候选择的。 光标在闪烁,目前已经进入 base 环境模式: …...

HTML大雪纷飞
目录 写在前面 HTML简介 完整代码 代码分析 运行结果 系列文章 写在后面 写在前面 小编又又又出现啦!这次小编给大家带来大雪纷飞HTML版,不需要任何的环境,只要有一个浏览器,就可以随时随地下一场大雪哦! HTM…...

问界新M7 Ultra仅售28.98万元起,上市即交付
5月31日,问界新M7 Ultra正式上市。发布会上,鸿蒙智行旗下多款产品交出最新答卷——问界新M5上市1个月大定突破2万台;智界S7位列30万纯电轿车4月交付量NO.3;问界M9上市5个月大定突破9万台。其中,作为中国高端豪华SUV市场…...

【Java数据结构】详解LinkedList与链表(四)
🔒文章目录: 1.❤️❤️前言~🥳🎉🎉🎉 2.什么是LinkedList 3.LinkedList的使用 3.1LinkedList的构造方法 3.2LinkedList的其他常用方法介绍 addAll方法 subList方法 LinkedList的常用方法总使…...
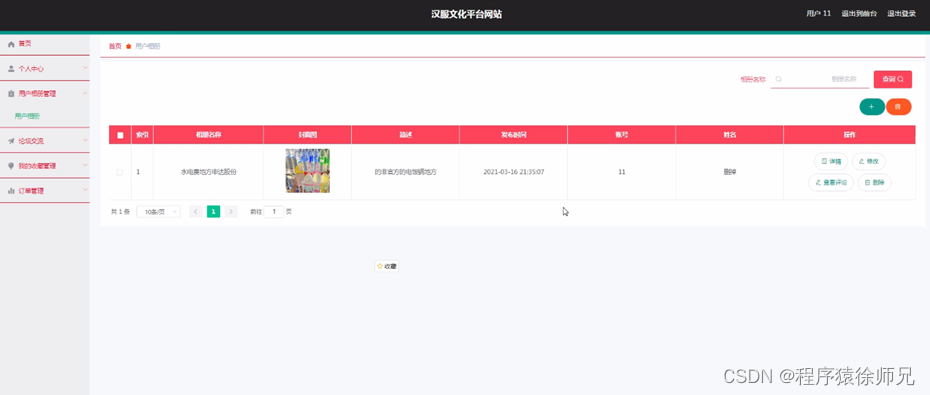
ssm汉服文化平台网站
博主介绍:✌程序员徐师兄、8年大厂程序员经历。全网粉丝15w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...

如何让 LightRoom 每次导入照片后不自动弹出 SD 卡 LR
如何让 LightRoom 每次导入照片后不自动弹出 SD 卡 LR 在导入窗口左上角有个选项: 导入后弹出 把这个去掉就可以了...

elasticdump和ESM
逐个执行如下命令; 1.拷贝analyzer如分词(需要分词器,可能不成功,不影响复制) ./elasticdump --inputhttp://[来源IP地址]:9200/[来源索引] --outputhttp://[目标IP地址]:9200/[目标索引] --typeanalyzer 2.拷贝映射…...
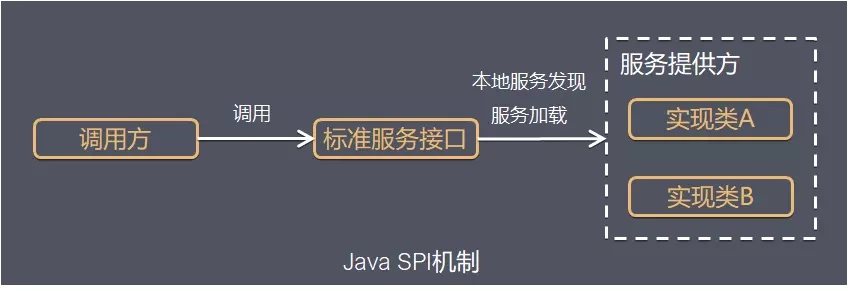
Java扩展机制:SPI与Spring.factories详解
一、SPI SPI全称Service Provider Interface,是Java提供的一套用来被第三方实现或者扩展的API,它可以用来启用框架扩展和替换组件。 整体机制图如下: Java SPI 实际上是“基于接口的编程+策略模式+配置文件”组合实现的动态加载机制。 系统设计的各个抽象,往往有很多不…...

iPhone 语言编程:深入探索与无限可能
iPhone 语言编程:深入探索与无限可能 在数字化时代的浪潮中,iPhone 作为一款全球领先的智能手机,其语言编程的奥秘一直吸引着众多开发者与爱好者的目光。iPhone 的语言编程不仅关乎技术实现,更涉及到用户体验、创新应用等多个层面…...

css动态导航栏鼠标悬停特效
charset "utf-8"; /*科e互联特效基本框架CSS*/ body, ul, dl, dd, dt, ol, li, p, h1, h2, h3, h4, h5, h6, textarea, form, select, fieldset, table, td, div, input {margin:0;padding:0;-webkit-text-size-adjust: none} h1, h2, h3, h4, h5, h6{font-size:12px…...

Vue中使用axios先获取头像上传参数然后上传图片到服务器-demo
这是一个使用axios发送POST请求上传图片到AWS S3的代码。其中: 引入了axios、FormData和fs模块;创建FormData实例,向其中添加上传图片的相关信息;创建axios请求的配置对象config,包含url、method、headers和data等属性…...
Win11环境下Android Studio中Flutter开发环境构建(逐步解决)
flutter开发环境构建 1. Flutter开发环境搭建1.1 Android Studio1.2 flutter下载flutter设置环境变量增加国内镜像 1.3 flutter doctorAndroid toolchain:cmdline-tools component is missingAndroid toolchain:Some Android licenses not acceptedChrom…...

Thread Servlet思考
在开发过程中我们经常会遇到两个对象分别是Thread和Servlet。但是很少会考虑到两者之前的关系。 Thread是线程,在tomcat服务器中请求被接收后,会启动线程对请求进行处理。线程会通过run方法执行实际执行的业务逻辑。在tomcat中当请求请求到线程池后&…...
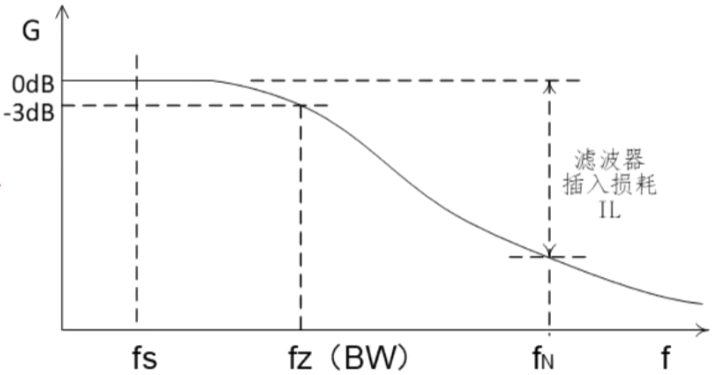
电源滤波器怎么选用
电源滤波器怎么选用 滤波器应用场景及作用第一步:第二步:第三步:第四步: 滤波器应用场景及作用 可以有效解决EMC测试无法通过、端口防护、滤除干扰、设备保护等问题 主要功能有: 1、降低主电源谐波; 2、保护驱动装置电力电子元件…...

终于更新了!时隔一年niushop多商户b2b2c的新补丁v5.0.2终于发布了,一起看看有啥新变化
注意这是最新版的V5.02_多商户V5.0.2版本更新说明 瞧瞧更新了什么内容, 优化功能 优化手机号、身份证等常用验证规则,全局化处理优化商品列表接口查询速度 修复功能修复系统内部分图片上传功能调用接口跨端口问题修复总后台和商家后台订单管理搜索标签在…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
