day46 完全背包理论基础 518. 零钱兑换 II 377. 组合总和 Ⅳ
完全背包理论基础
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
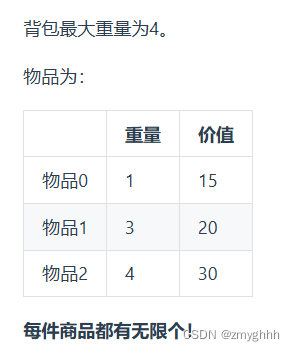
01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的,所以要从小到大去遍历
动规五部曲
1.确定dp数组的定义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
2.一维dp数组的递推公式
dp[j]为 容量为j的背包所背的最大价值,那么如何推导dp[j]呢?
dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,
3.一维dp数组如何初始化
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
4.一维dp数组遍历顺序
因为物品有无限个所以内层循环可以正序遍历重复放入。
再来看看两个嵌套for循环的顺序,代码中是先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?
可以!
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序是无所谓的!因为两个for循环都是正序遍历,物品有无数个,先遍历物品与先遍历背包得到的结果是相同的,所以遍历顺序可以改变。因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。

// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
// 先遍历背包,再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量for(int i = 0; i < weight.size(); i++) { // 遍历物品if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}5.举例推导dp数组
52. 携带研究材料(典型完全背包问题)
在本题(现有代码基础上)中需要先遍历物品再遍历背包如果先遍历背包再遍历物品由于这个题目是在第一层循环内输入weight和value这样会导致多输入一组 数据(dp数组的长度为背包容量加1方便取到dp[w],防止数组越界),解决:只有使用一次for循环(weight和value数组长度为n)来填充weight和value数组来存储数据再做操作即可(如下面第二段代码)。
代码
import java.util.*;
import java.lang.*;public class Main{public static void main (String[] args) {Scanner in = new Scanner(System.in);int n = in.nextInt();int w = in.nextInt();int[] dp = new int[w+1];for (int i = 0; i < n; ++i) {int weight = in.nextInt();int value = in.nextInt();for (int j = weight; j <= w; ++j)dp[j] = Math.max(dp[j], dp[j-weight] + value);}// for(int i = 0 ; i< = w ; i++){// int weight = in.nextInt();// int value = in.nextInt();// for(int j = 0; j < n; j++){// if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight] + value);// }// }System.out.println(dp[w]);}
}import java.util.*;
import java.lang.*;public class Main{public static void main (String[] args) {Scanner in = new Scanner(System.in);int n = in.nextInt();int w = in.nextInt();int[] dp = new int[w+1];int [] weight = new int [n];int [] value = new int [n];for (int i = 0; i < n; ++i) {int weights = in.nextInt();int values = in.nextInt();weight[i] = weights;value[i] = values;}// for(int num : weight){// System.out.print(num+",");// }// System.out.println();// for(int nums : value){// System.out.print(nums+",");// }for(int i = 0 ; i<= w ; i++){for(int j = 0; j < n; j++){if (i - weight[j] >= 0) dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);}}System.out.println(dp[w]);}
}518. 零钱兑换 II
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物品组合个数!
组合不强调元素之间的顺序,排列强调元素之间的顺序。
动规五步曲
1.确定dp数组以及下标的含义
dp[j]:凑成总金额j的货币组合数为dp[j]
2.确定递推公式
dp[j] 就是所有的dp[j - coins[i]](考虑coins[i]的情况)相加。
所以递推公式:dp[j] += dp[j - coins[i]];
只要搞到nums[i],凑成dp[j]就有dp[j - nums[i]] 种方法。
例如:dp[j],j 为5,
- 已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 容量为5的背包。
- 已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 容量为5的背包。
- 已经有一个3(nums[i]) 的话,有 dp[2]中方法 凑成 容量为5的背包
- 已经有一个4(nums[i]) 的话,有 dp[1]中方法 凑成 容量为5的背包
- 已经有一个5 (nums[i])的话,有 dp[0]中方法 凑成 容量为5的背包
那么凑整dp[5]有多少方法呢,也就是把 所有的 dp[j - nums[i]] 累加起来。
3.dp数组如何初始化
首先dp[0]一定要为1,dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话,后面所有推导出来的值都是0了。下标非0的dp[j]初始化为0,这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]。
4.确定遍历顺序
纯完全背包求得装满背包的最大价值是多少,和凑成总和的元素有没有顺序没关系,即:有顺序也行,没有顺序也行!
而本题要求凑成总和的组合数,元素之间明确要求没有顺序。
外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)的情况。(组合)
for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量dp[j] += dp[j - coins[i]];}
}假设:coins[0] = 1,coins[1] = 5。
那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。
外层for循环遍历背包(金钱总额),内层for遍历物品(钱币)的情况。(排列)
for (int j = 0; j <= amount; j++) { // 遍历背包容量for (int i = 0; i < coins.size(); i++) { // 遍历物品if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];}
}背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。
5.举例推导dp数组
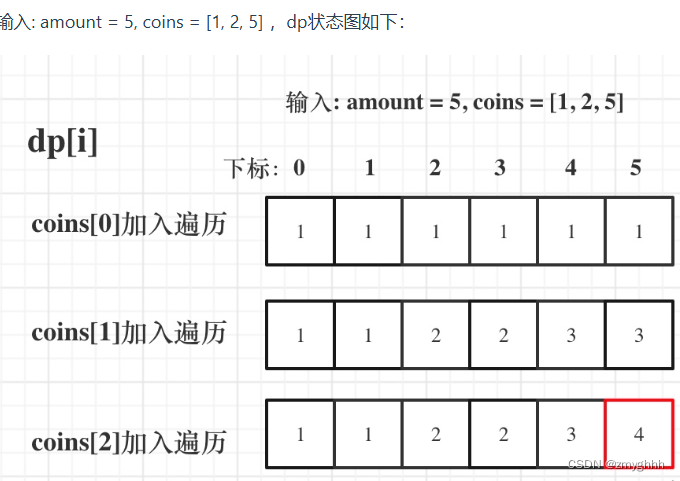
//先物品后背包 class Solution {public int change(int amount, int[] coins) {int n = coins.length;int[] dp = new int[amount + 1];Arrays.fill(dp, 0);dp[0] = 1;for (int i = 0; i < n; i++) {for(int j = coins[i]; j<=amount;j++){dp[j] += dp[j-coins[i]];}}return dp[amount];}}377. 组合总和 Ⅳ
本题题目描述说是求组合,但又说是可以元素相同顺序不同的组合算两个组合,其实就是求排列!
组合不强调顺序,(1,5)和(5,1)是同一个组合。
排列强调顺序,(1,5)和(5,1)是两个不同的排列。
动规五部曲
1.确定dp数组以及下标的含义
dp[i]: 凑成目标正整数为i的排列个数为dp[i]
2.确定递推公式
dp[i] += dp[i - nums[j]];
3.dp数组如何初始化
因为递推公式dp[i] += dp[i - nums[j]]的缘故,dp[0]要初始化为1,这样递归其他dp[i]的时候才会有数值基础。
至于dp[0] = 1 有没有意义呢?
其实没有意义,所以我也不去强行解释它的意义了,因为题目中也说了:给定目标值是正整数! 所以dp[0] = 1是没有意义的,仅仅是为了推导递推公式。
至于非0下标的dp[i]应该初始为多少呢?
初始化为0,这样才不会影响dp[i]累加所有的dp[i - nums[j]]。
4.确定遍历顺序
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
5.举例来推导dp数组

class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target + 1];dp[0] = 1;for (int i = 0; i <= target; i++) {for (int j = 0; j < nums.length; j++) {if (i >= nums[j]) {dp[i] += dp[i - nums[j]];}}}return dp[target];}
}二维解法
public class ALL {public static void main(String[] args) {int[] coins = new int[]{1, 2, 5};int amount = 5;int result = change(5, coins);System.out.println(result);}public static int change(int amount, int[] coins) {int[][] dp = new int[amount + 1][coins.length+1];dp[0][0] = 1;// weight数组的大小 就是物品个数for (int i = 1; i <= amount; i++) { // 遍历背包容量for (int j = 1; j <= coins.length; j++) { // 遍历物品,统一下标if (coins[j - 1] <= i) { //保证背包容量比物品容量大for (int k = 0; k <= coins.length; k++) { //对列进行操作 找出满足某一个背包容量的“组合数”有多少dp[i][j] += dp[i - coins[j-1]][k];}}}}int res = 0;for (int i = 0; i <= coins.length; i++) { /最后对满足背包容量的所有组合加起来即为排列res += dp[amount][i];}return res;}}相关文章:

day46 完全背包理论基础 518. 零钱兑换 II 377. 组合总和 Ⅳ
完全背包理论基础 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。 01背包内嵌的循环是从…...
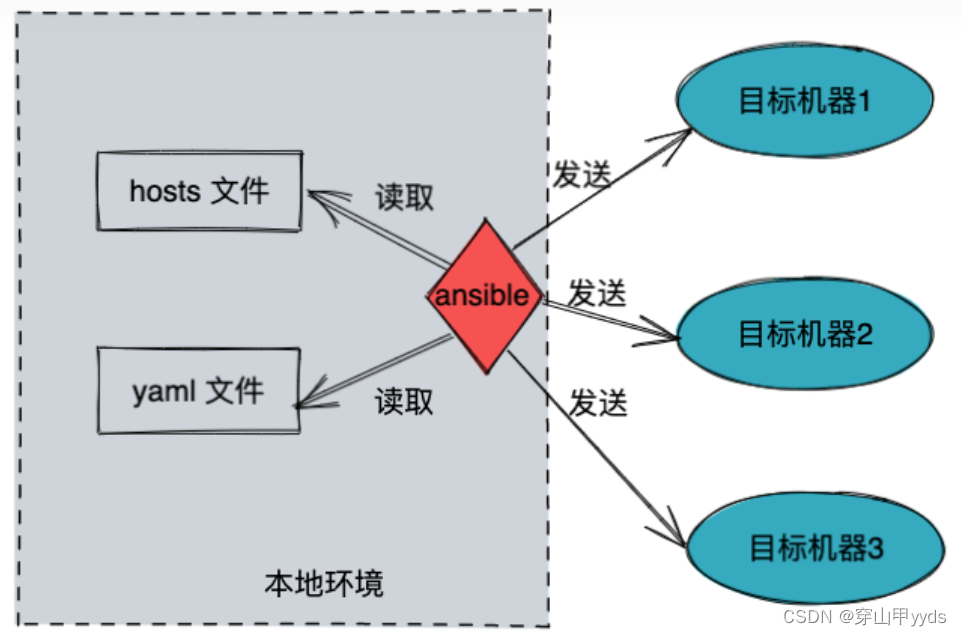
【linux】运维-基础知识-认知hahoop周边
1. HDFS HDFS(Hadoop Distributed File System)–Hadoop分布式文件存储系统 源自于Google的GFS论文,HDFS是GFS的克隆版 HDFS是Hadoop中数据存储和管理的基础 他是一个高容错的系统,能够自动解决硬件故障,eg:…...
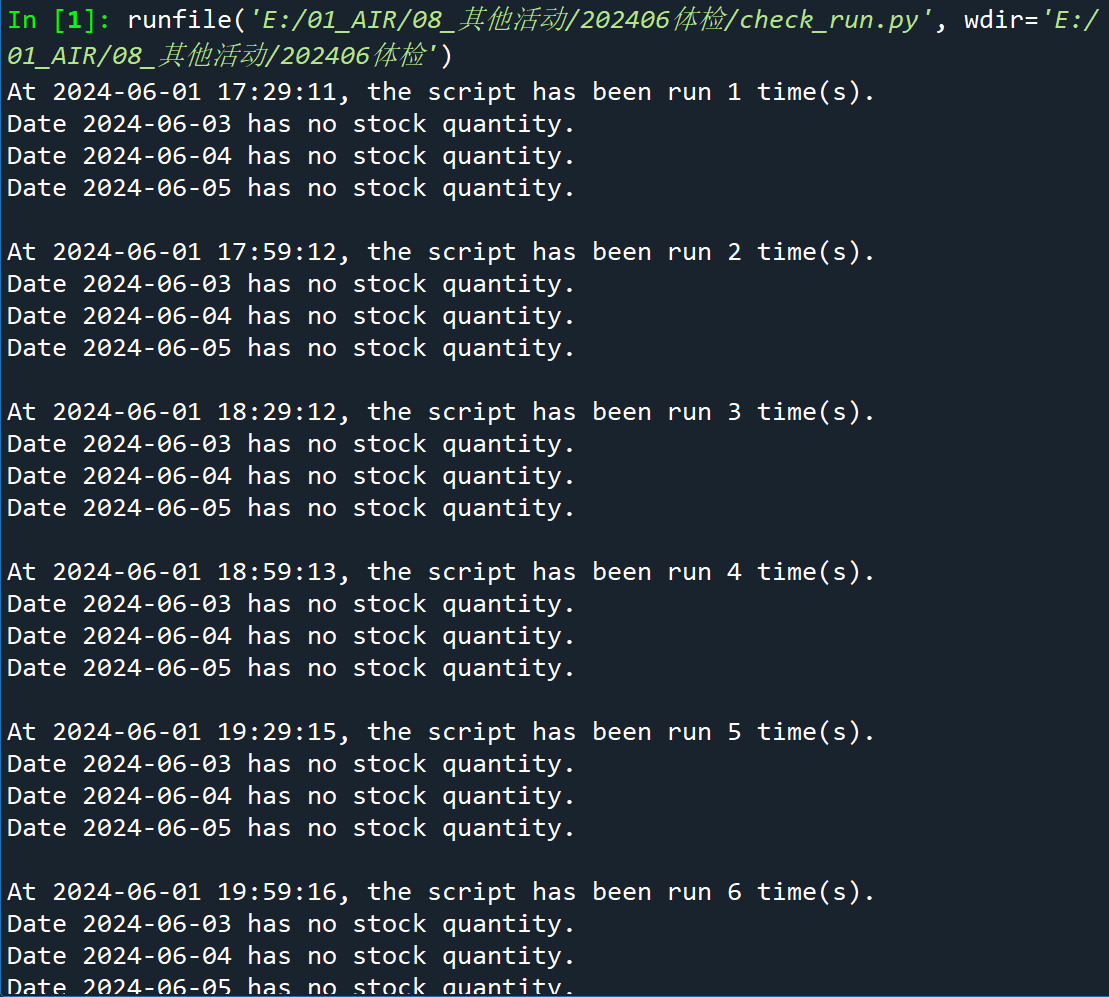
Python自动实时查询预约网站的剩余名额并在有余额时发邮件提示
本文介绍基于Python语言,自动、定时监测某体检预约网站中指定日期的体检余额,并在有体检余额时自动给自己发送邮件提醒的方法。 来到春招末期,很多单位进入了体检流程。其中,银行(尤其是四大行)喜欢“海检”…...
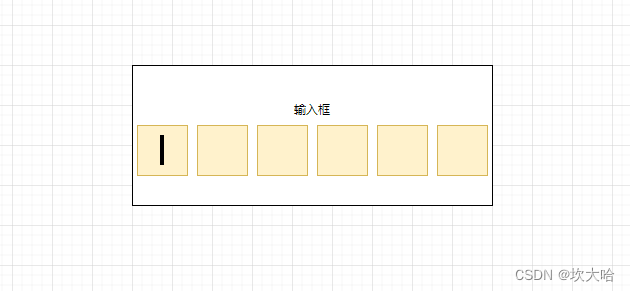
Flutter 验证码输入框
前言: 验证码输入框很常见:处理不好 bug也会比较多 想实现方法很多,这里列举一种完美方式,完美兼容 软键盘粘贴方式 效果如下: 之前使用 uniapp 的方式实现过一次 两种方式(原理相同)࿱…...

如何从0到设计一个CRM系统
什么是CRM 设计开始之前,先来了解一下什么是CRM。CRM(Customer Relationship Management)是指通过建立和维护与客户的良好关系,达到满足客户需求、提高客户满意度、增加业务收入的一种管理方法和策略。CRM涉及到跟踪和管理客户的所…...
Numba 的 CUDA 示例 (2/4):穿针引线
本教程为 Numba CUDA 示例 第 2 部分。 按照本系列从头开始使用 Python 学习 CUDA 编程 介绍 在本系列的第一部分中,我们讨论了如何使用 GPU 运行高度并行算法。高度并行任务是指任务完全相互独立的任务,例如对两个数组求和或应用任何元素函数。 在本教…...

项目的各个阶段如何编写标准的Git commit消息
标准提交消息格式 一个标准的提交消息应包括三部分:标题(summary)、正文(description)和脚注(footer)。 1. 标题(Summary) 简洁明了,不超过50个字符。使用…...
Python课设-学生信息管理系统
一、效果展示图 二、前端代码 1、HTML代码 <1>index.html <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0">…...

openssl 常用命令demo
RSA Private Key的结构(ASN.1) RSAPrivateKey :: SEQUENCE { version Version, modulus INTEGER, -- n publicExponent INTEGER, -- e privateExponent INTEGER, -- d prime1 INTEGER, -- …...

【Linux】Linux基本指令2
目录 1.man指令(重要): 2.echo指令 3.cp指令(重要): 4.mv指令 5.cat指令/echo指令重定向 6.more指令 7.less指令(重要) 8.head指令 9.tail指令 我们接着上一篇:h…...

springboot+vue+mybatis博物馆售票系统+PPT+论文+讲解+售后
如今社会上各行各业,都喜欢用自己行业的专属软件工作,互联网发展到这个时候,人们已经发现离不开了互联网。新技术的产生,往往能解决一些老技术的弊端问题。因为传统博物馆售票系统信息管理难度大,容错率低,…...
java—MyBatis框架
简介 什么是 MyBatis? MyBatis 是一款优秀的持久层框架,它支持自定义 SQL、存储过程以及高级映射。MyBatis 免除了几乎所有的 JDBC 代码以及设置参数和获取结果集的工作。MyBatis 可以通过简单的 XML 或注解来配置和映射原始类型、接口和 Java POJO&…...

如何使用Spring Cache优化后端接口?
Spring Cache是Spring框架提供的一种缓存抽象,它可以很方便地集成到应用程序中,用于提高接口的性能和响应速度。使用Spring Cache可以避免重复执行耗时的方法,并且还可以提供一个统一的缓存管理机制,简化缓存的配置和管理。 本文将详细介绍如何使用Spring Cache来优化接口,…...

大话C语言:第21篇 数组
1 数组概述 数组是若干个相同类型的变量在内存中有序存储的集合。 数组是 C 语言中的一种数据结构,用于存储一组具有相同数据类型的数据。 数组在内存中会开辟一块连续的空间 数组中的每个元素可以通过一个索引(下标)来访问,索…...

transfomer中attention为什么要除以根号d_k
简介 得到矩阵 Q, K, V之后就可以计算出 Self-Attention 的输出了,计算的公式如下: A t t e n t i o n ( Q , K , V ) S o f t m a x ( Q K T d k ) V Attention(Q,K,V)Softmax(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)Softmax(dk QKT)V 好处 除以维…...
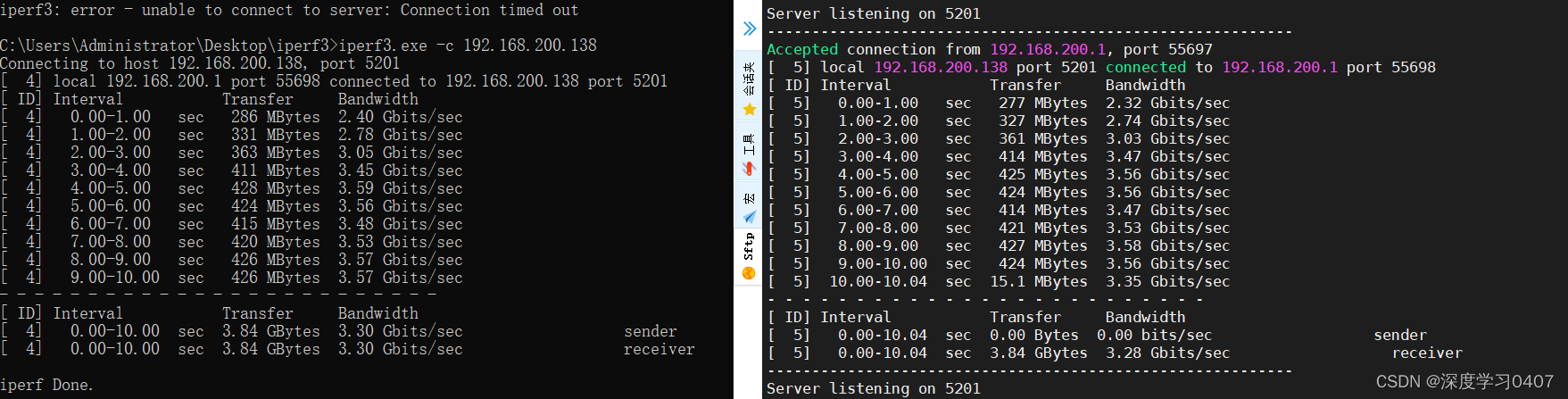
iperf3带宽压测工具使用
iperf3带宽压测工具使用 安装下载地址:[下载入口](https://iperf.fr/iperf-download.php)测试结果:时长测试(压测使用):并行测试反向测试UDP 带宽测试 iPerf3 是用于主动测试 IP 网络上最大可用带宽的工具 安装 下载地址&#x…...

[数据集][目标检测]焊接处缺陷检测数据集VOC+YOLO格式3400张8类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):3400 标注数量(xml文件个数):3400 标注数量(txt文件个数):3400 标注…...
)
2024华为OD机试真题-剩余银饰的重量-C++(C卷D卷)
题目描述 有 N 块二手市场收集的银饰,每块银饰的重量都是正整数,收集到的银饰会被熔化用于打造新的饰品。 每一回合,从中选出三块 最重的 银饰,然后一起熔掉。假设银饰的重量分别为 x 、y 和 z, 且 x <= y <= z。那么熔掉的可能结果如下: 如果x == y == z,那么三…...

糖果促销【百度之星】/思维
糖果促销 思维 大佬的解法: #include<bits/stdc.h> using namespace std; typedef long long ll; int main() {ll t;cin>>t;for(int i0;i<t;i){ll p,k;cin>>p>>k;if(k0) cout<<0<<endl;else{k-(k-1)/p;cout<<k<…...
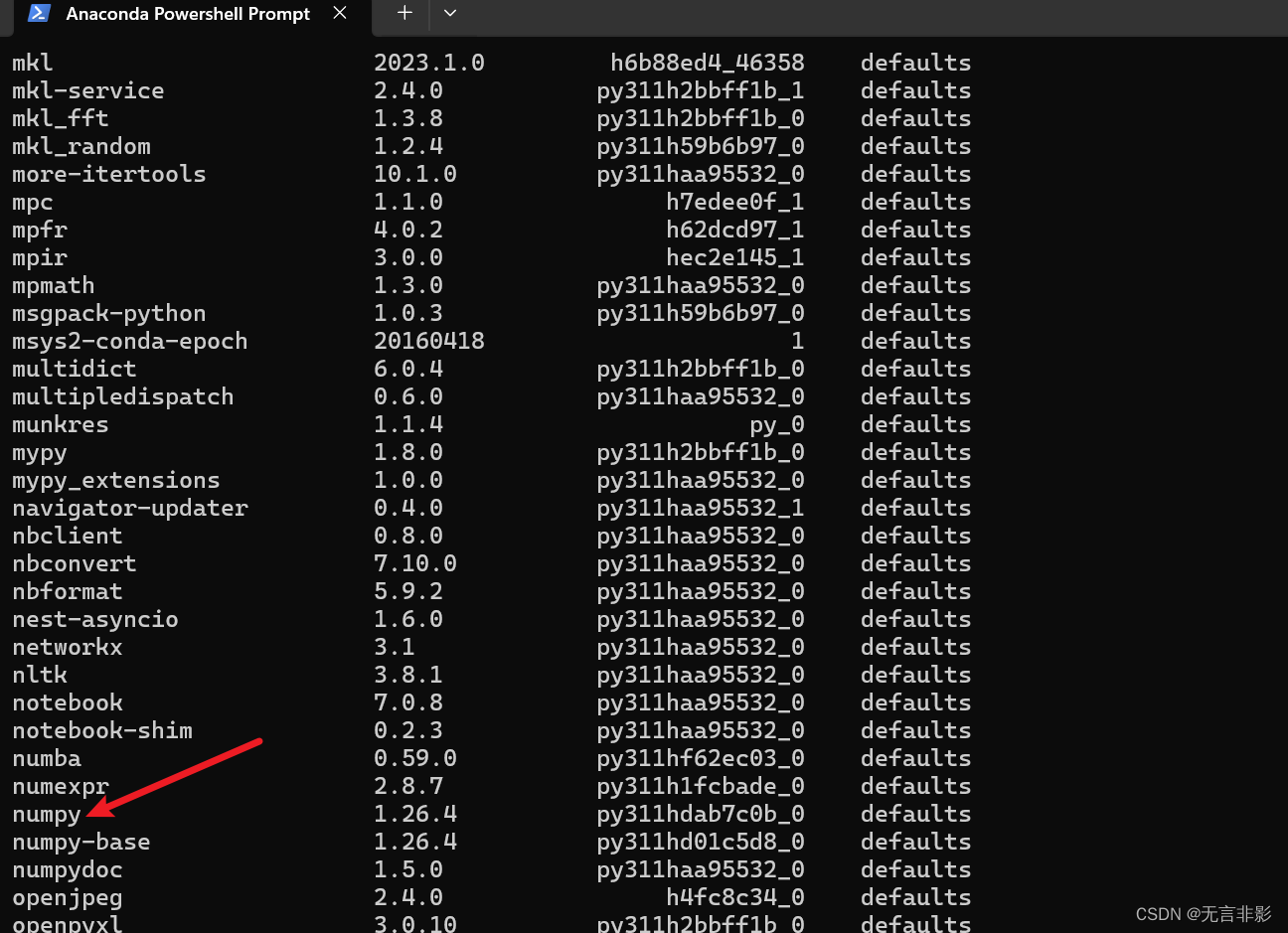
【python学习】安装Anaconda后,如何进行环境管理(命令行操作及图形化操作Anaconda Navigator)及包管理
命令行的方式 首先,打开 Anaconda Powershell Prompt 环境查看 使用以下命令查看当前所有环境: conda env list目前只有一个 base环境,就是安装 anaconda的时候选择的。 光标在闪烁,目前已经进入 base 环境模式: …...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
