R语言探索与分析-美国房价及其影响因素分析
一、选题背景
以多元线性回归统计模型为基础,用R语言对美国部分地区房价数据进行建模预测,进而探究提高多元回 归线性模型精度的方法。先对数据进行探索性预处理,随后设置虚拟变量并建模得出预测结果,再使用方差膨胀因子对 多重共线性进行修正,从而提高模型精度与稳健性,使回归结果在很大程度上得到优化。...
近年来,随着经济的不断增长,飞速增长的房价仍然是民众心中最看重的问题之一。房地产行业是我国经济健康发展的稳定器,也是加快我国经济增长的助力器,不仅对经济社会起着重要的支撑作用,还对社会的稳定产生着难以衡量的影响。
二、文献综述
...
三、方案论证(设计理念)
多元线性回归具有非常广泛的应用范围,但在实 际预测中对存在类别变量设置不充分或多重共线性 问题,导致统计模型缺乏精度和稳健性。由此,本文对如何精准且高效的排除多重共线性影响,并合理地 将分类变量转化为虚拟变量,提升多元线性回归模型 精度作了进一步探索,并将其应用于房价预测上。
四、实证分析
在美国房屋信息数据集中,包含不同地区的平均房价及多个可能影响房价的自变量:AvgAreaIncome(该地区的平均收入) AvgAreaHouseAge (房子的平均面积)AreaPopulation(该地区的人口数量)等。首先进行数据展示
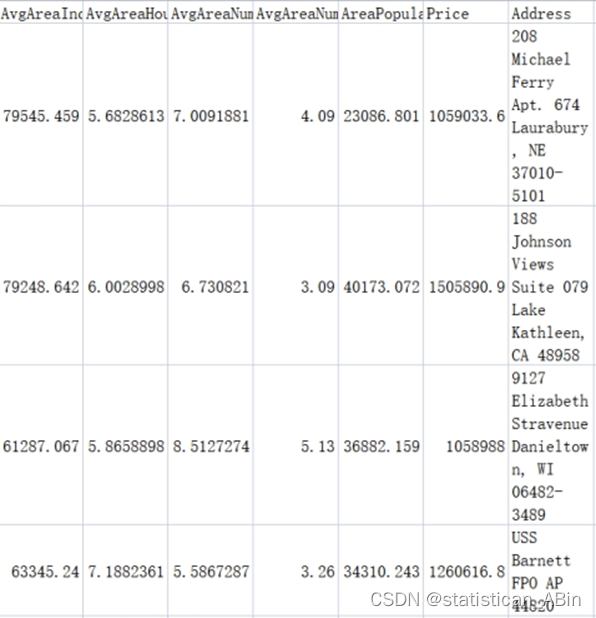
随后读取数据并且进行描述性统计
library(openxlsx)
# 文件名+sheet的序号
dataset<- read.xlsx("house.xlsx", sheet = 1)
#View(dataset)
datasetsummary(dataset)#####描述性统计分析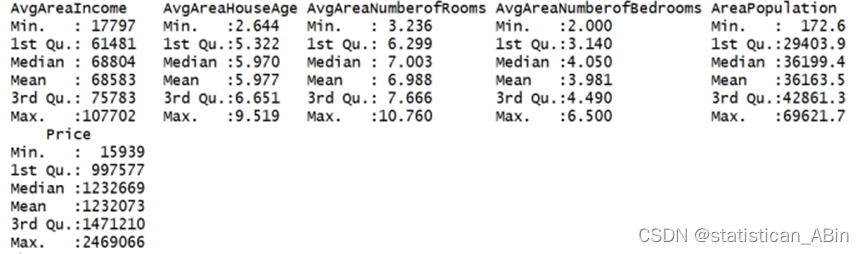
具体描述性统计如上,包括各个变量的最大值、最小值、中位数、1/4分位数和3/4分位数等
接下来画出价格、该地区的平均收入的柱状图查看情况:


###画出price柱状图
price<-dataset$Price
pricehead(price,n=100)
barplot(head(price,n=100),xlab="house",ylab="prcie",col="blue",main="房价柱状图(前100个)",border="red")####画出该地区的平均收入柱状图
income<-dataset$AvgAreaIncome
incomehead(income,n=100)
barplot(head(income,n=100),xlab="",ylab="收入",col="pink",main="该地区的平均收入柱状图(前100个)",border="green")
画出特征变量的箱线图,看其分布形状,如图所示:

由图可得,6个特征变量均分布较好且,存在异常值但是异常值很少。
接下来运用热力图展示出特征变量与响应变量的关系图:

从相关系数热力图可以看出,几乎每个特征变量对房价的相关系数都较高,但是其中该地区的平均收入与房价的相关系数是最高的,为0.64。
再用ggpairs函数展示出变量间的相关性,以及从下图中的相关系数中也可得出其相关性。

接下来用房价对最初的特征变量进行回归,结果如下:
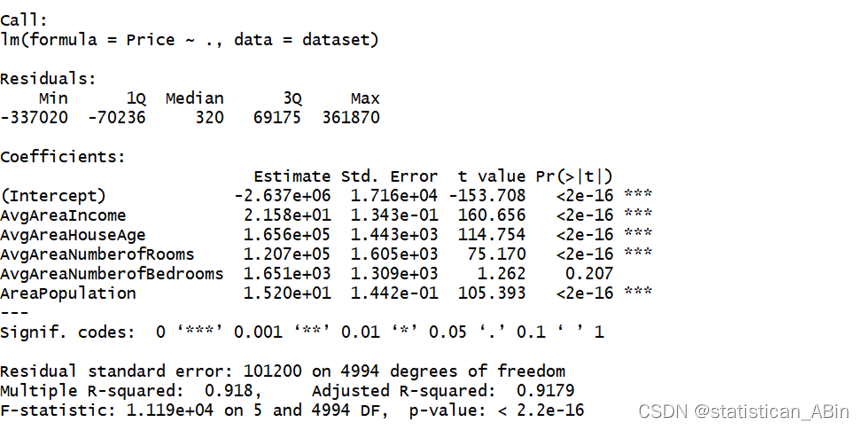
图为软件R计算的结果。R²反应了全部6个x与y之间的线性相关水平。其中调整后的拟合优度为0.9179,接近于1,表明该模型对数据的拟合程度比较好,并且可以说明Price的91.79%可由这些因素来解释。P值<0.01,说明p的值非常的小,表明有99%的把握认为至少有一个解释变量是属于这个回归方程的,但这只能说明模型总体是显著的,且*号越多影响越显著。
运用向后逐步回归,每次计算AIC值不断剔除一个变量,利用其余变量进行回归,最终方程为:
 接下来进行模型检验
接下来进行模型检验
表 1 异方差检验结果
| Stufentsized Breusch-Pagan test |
| Data: fit1 |
| BP= 10.385, df=4 , p_value=0.03441 |
由于p值小于0.05,拒绝原假设,可认为该模型不存在异方差性。
接下来,画出回归值与残差的残差图

五、结论
本次实验完整的研究了多元线性回归模型,首先简单的介绍了多元线性回归模型及其相关的基本理论,然后运用 R 语言实现多元回归模型的拟合,学习了如何求变量间的相关系数矩阵和画散点图矩阵,然后运用 lm 函数拟合回归模型,并运用赤池信息准则选择最优模型,最终对拟合的最优模型进行预测。
代码加数据
代码加数据加报告
创作不易,希望大家多多点赞收藏和评论!
相关文章:

R语言探索与分析-美国房价及其影响因素分析
一、选题背景 以多元线性回归统计模型为基础,用R语言对美国部分地区房价数据进行建模预测,进而探究提高多元回 归线性模型精度的方法。先对数据进行探索性预处理,随后设置虚拟变量并建模得出预测结果,再使用方差膨胀因子对 多重共…...
Android14 WMS-窗口添加流程(一)-Client端
窗口布局在onCreate方法中通过setContentView(R.layout.xxx)加载,但窗口的显示并不是在wm_on_create_called中, 而是在wm_on_resume_called后,也就是说应用onResume时此窗口是不可见的,真正可见是当此window窗口的mDrawState变化状态从NO_SUR…...
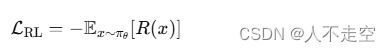
【人工智能】第二部分:ChatGPT的架构设计和训练过程
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...

Informer
I n f o r m e r Informer Informer 摘要: 长序列时间序列的预测 i n f o r m e r informer informer优点: P r o b s p a r e Probspare Probspare自关注机制,在时间复杂度和内存使用方面达到 O ( N l o g N ) O(NlogN) O(NlogN),在序列依…...

12岁学什么编程机构好:深入剖析与全面指导
12岁学什么编程机构好:深入剖析与全面指导 在数字化时代,编程已成为一项必备技能。对于12岁的孩子来说,选择一个合适的编程机构至关重要。然而,市场上的编程机构众多,如何选择成为了一个难题。本文将从四个方面、五个…...

Day60 柱状图中最大的矩形
84 柱状图中最大的矩形 题目链接:84. 柱状图中最大的矩形 - 力扣(LeetCode) 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的…...

typescript --object对象类型
ts中的object const obj new Object()Object 这里的Object是Object类型,而不是JavaScript内置的Object构造函数。 这里的Object是一种类型,而Object()构造函数表示一个值。 Object()构造函数的ts代码 interface ObjectConstructor{readonly prototyp…...

如何使用python将多个EXCEL表进行合并
在Python中,你可以使用pandas库来轻松地将多个Excel表格合并。以下是一个基本的步骤指南和示例代码,说明如何合并多个Excel文件到一个单独的DataFrame中: 步骤 安装pandas和openpyxl(如果你正在处理.xlsx文件)。导入…...

【前端每日基础】day35——HTML5离线存储
HTML5引入了一些新的特性和API来增强Web应用的功能,其中之一就是离线存储。离线存储允许Web应用在没有网络连接的情况下仍能正常运行。以下是HTML5离线存储的主要技术和详细介绍: Web Storage (LocalStorage 和 SessionStorage) LocalStorage 概述&…...

动态规划算法:背包问题
背包问题概述 背包问题 (Knapsack problem) 是⼀种组合优化的 NP完全问题 。 问题可以描述为:给定⼀组物品,每种物品都有⾃⼰的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最⾼。 根据物品的个…...
新版idea配置git步骤及项目导入
目录 git安装 下载 打开git Bash 配置全局用户名及邮箱 查看已经配置的用户名和邮箱 在IDEA中设置Git 问题解决 项目导入 前言-与正文无关 生活远不止眼前的苦劳与奔波,它还充满了无数值得我们去体验和珍惜的美好事物。在这个快节奏的世界中࿰…...
)
赶紧收藏!2024 年最常见 20道 Kafka面试题(一)
一、Kafka都有哪些特点? Kafka是一个分布式流处理平台,它被设计用于高吞吐量的数据管道和流处理。以下是Kafka的一些主要特点: 高吞吐量、低延迟:Kafka每秒可以处理数十万条消息,延迟可以低至几毫秒。这是通过优化数据…...

unsigned char*和const char*的一些问题
1.可以返回字符串常量,但是不能返回char buf[BUF_SIZE] char* get_str(){char* str "hello world";return str; }char* get_str(){char str[32] {0};strcpy(str, "hello world");return str; }//err 2.联合体不能用指针,也…...

前端知识1-4:性能优化进阶
性能优化进阶 Navigation Timing API navigationStart / end 表示从上一个文档卸载结束时 > 如果没有上一个文档,这个值和fetchStart相等 unloadEventStart / end 标识前一个网页unload的时间点 redirectStart / end 第一个http重定向发生和结束的时间 fetch…...

ios 新安装app收不到fcm推送
🏆本文收录于「Bug调优」专栏,主要记录项目实战过程中的Bug之前因后果及提供真实有效的解决方案,希望能够助你一臂之力,帮你早日登顶实现财富自由🚀;同时,欢迎大家关注&&收藏&&…...
汽美汽修店管理系统会员小程序的作用是什么
汽车后市场汽美汽修赛道同样存在着大量商家,连锁品牌店或个人小店等,门店扎堆且区域覆盖面积广,当然每天车来车往也有不少生意。 随着线上化程度加深和商家不断拓展市场的需要,传统运营模式可能难以满足现状,尤其是年…...
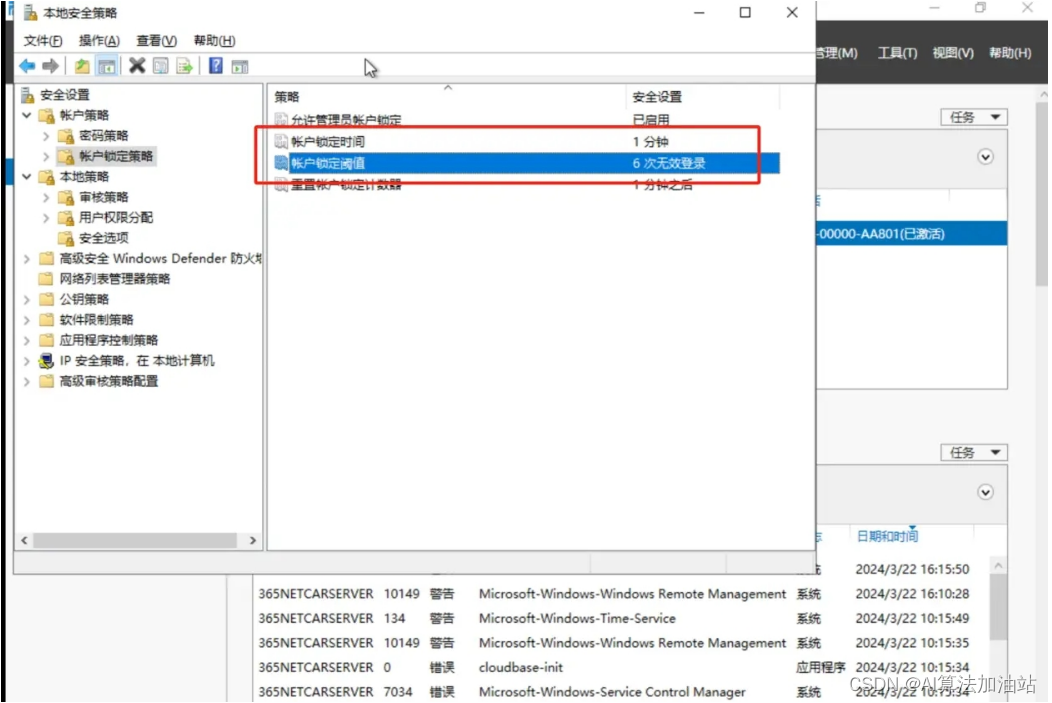
远程自动锁定平面
目录 Ubuntu 系统上 方法一:使用 SSH 重新连接 方法二:解锁当前会话 方法三:通过 SSH 解锁会话 方法四:禁用自动锁屏(如果合适) windows系统 方法三:修改组策略设置 Ubuntu 系统上 远程…...

鸿蒙Ability Kit(程序框架服务)【UIAbility组件与UI的数据同步】
UIAbility组件与UI的数据同步 基于当前的应用模型,可以通过以下几种方式来实现UIAbility组件与UI之间的数据同步。 [使用EventHub进行数据通信]:在基类Context中提供了EventHub对象,可以通过发布订阅方式来实现事件的传递。在事件传递前&am…...

一个完整的springboot项目,我们还需要做什么
文章目录 一 从0创建Srpingboot项目1.1 启动springboot项目1.2 导入必要的依赖 二、还缺什么2.1 统一异常捕获2.2 统一MVC返回2.3 数据分层2.4 连接数据库模块2.5 放置常量和工具类2.6 基础controller、基础entity、query查询类2.7 为了方便处理异常,一般还可以入参…...

QT-界面居中管理
问题:为什么不能对checkbox直接居中,LineEdit可以 复选框是一个固定大小的控件,不适合填满整个单元格,而相比之下QLineEdit是一个可变大小的控件 关于居中: lineEdit:lineEdit -> setAlignment(QT::Al…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

Gitlab + Jenkins 实现 CICD
CICD 是持续集成(Continuous Integration, CI)和持续交付/部署(Continuous Delivery/Deployment, CD)的缩写,是现代软件开发中的一种自动化流程实践。下面介绍 Web 项目如何在代码提交到 Gitlab 后,自动发布…...
