最小时间差

首先可以想到,可以计算出任意两个时间之间的差值,然后比较出最小的,不过这种蛮力方法时间复杂度是O(n^2)。而先将时间列表排序,再计算相邻两个时间的差值,就只需要计算n个差值,而排序阶段时间复杂度通常为O(nlogn),所以优化后的时间复杂度为O(nlogn)。
不过需要注意的是还需要考虑第一个和最后一个时间点跨越午夜的时间差的大小。并且一天只有1440分钟,如果时间列表大于1440,那么必然有重复的时间点,最小差值即为0。
class Solution {public int findMinDifference(List<String> timePoints) {int n = timePoints.size();// 由于一天最多有1440分钟,如果timePoints超过1440个,那么必然有重复的时间点,最小差值为0if (n > 1440) {return 0;}// 将时间点按字符串排序,默认是按HH:MM的字典顺序排序Collections.sort(timePoints);int ans = Integer.MAX_VALUE;// 获取第一个时间点的分钟数int t0Minutes = getMinutes(timePoints.get(0));// 初始化上一个时间点为第一个时间点int preMinutes = t0Minutes;// 从第二个时间点开始,逐个计算与前一个时间点的时间差for (int i = 1; i < n; ++i) {int minutes = getMinutes(timePoints.get(i));// 计算相邻时间点的时间差并保留最小的ans = Math.min(ans, minutes - preMinutes); preMinutes = minutes; // 更新上一个时间点为当前时间点}// 计算第一个和最后一个时间点跨越午夜的时间差ans = Math.min(ans, t0Minutes + 1440 - preMinutes);return ans;}// 将时间点转换为分钟数的方法,比如输入“10:01”返回601public int getMinutes(String t) {return ((t.charAt(0) - '0') * 10 + (t.charAt(1) - '0')) * 60 + ((t.charAt(3) - '0') * 10 + (t.charAt(4) - '0'));}
}相关文章:

最小时间差
首先可以想到,可以计算出任意两个时间之间的差值,然后比较出最小的,不过这种蛮力方法时间复杂度是O(n^2)。而先将时间列表排序,再计算相邻两个时间的差值,就只需要计算n个差值,而排序阶段时间复杂度通常为O…...
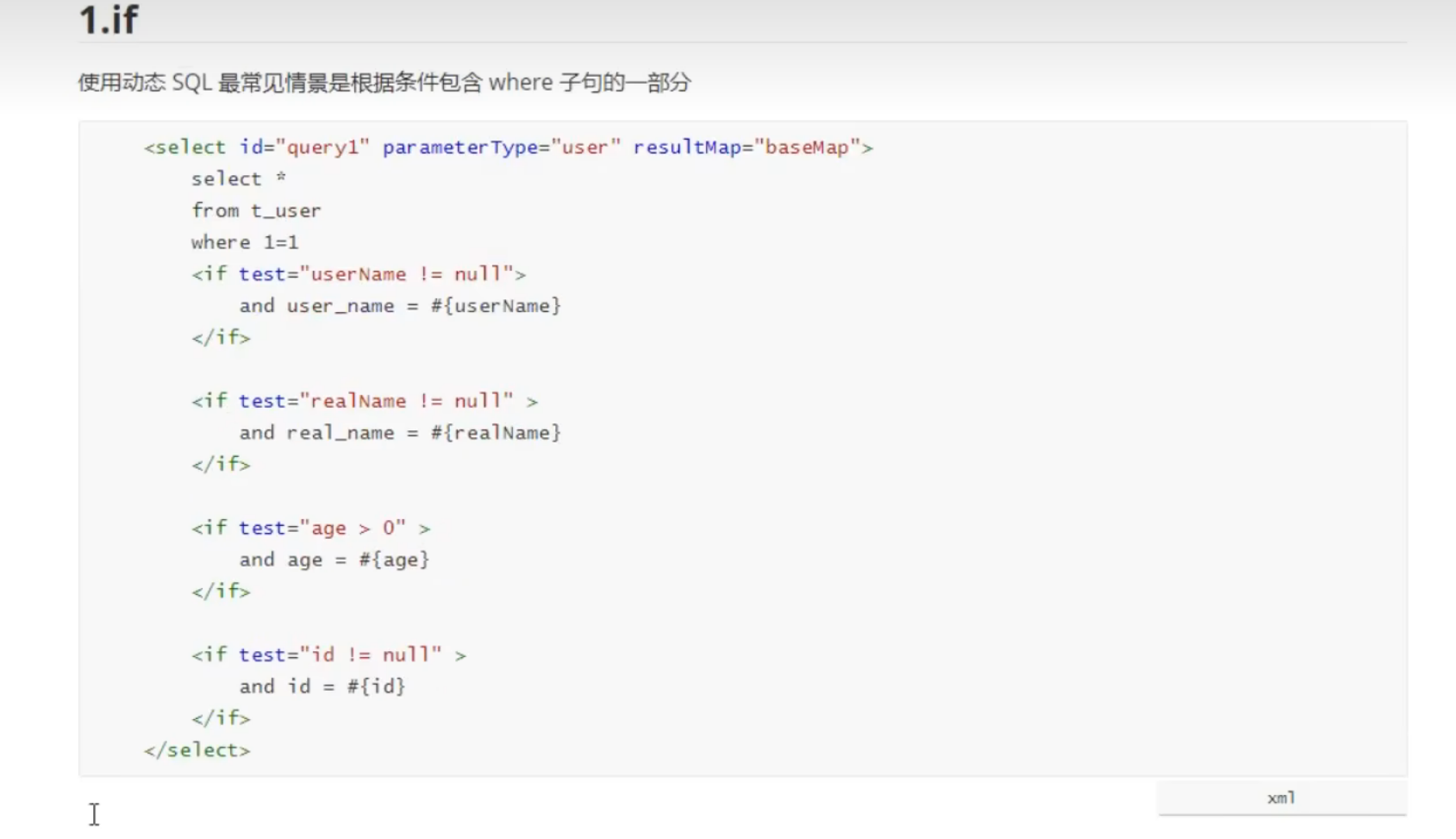
动态SQL IF语句
IF语句学习 第一种写法(标准) 我们先来看以下标准写法: select * from .. <where> <if test""> and ....... <if test""> and ....... <where> 我们用了一个where标签 , 内嵌if语句 第二种写法: 这是第二种写法:不用where标…...
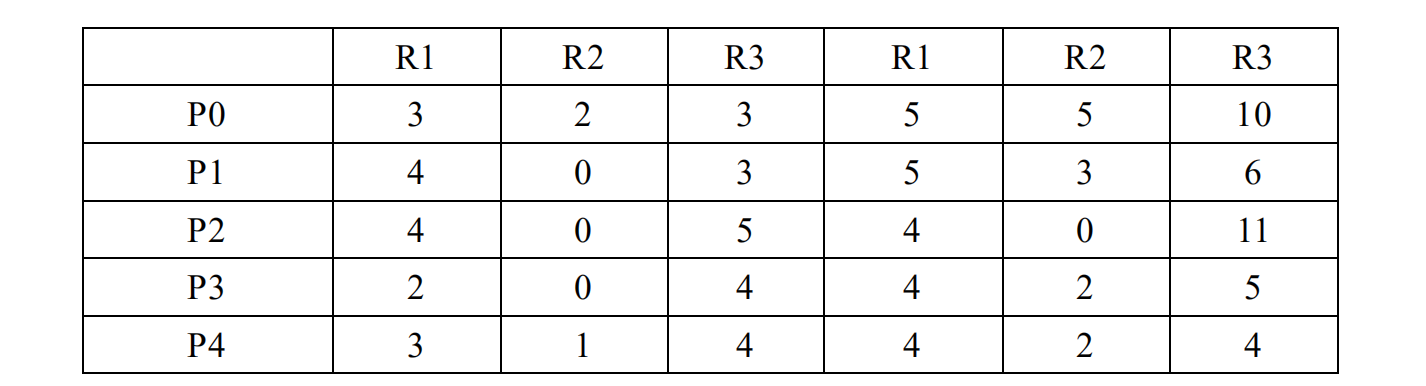
961题库 北航计算机 操作系统 附答案 选择题形式
有题目和答案,没有解析,不懂的题问大模型即可,无偿分享。 第1组 习题 计算机系统的组成包括( ) A、程序和数据 B、处理器和内存 C、计算机硬件和计算机软件 D、处理器、存储器和外围设备 财务软件是一种ÿ…...

SylixOS 版本与 RealEvo-IDE 版本对应关系说明
SylixOS 版本与 RealEvo-IDE 版本对应关系说明 SylixOS 版本IDE 版本发布日期1.4.13.1.52017/01/171.5.23.5.12017/10/121.7.13.8.32018/06/221.8.33.9.52018/10/081.9.9-103.9.102020/01/021.11.63.10.22020/05/131.11.73.10.x2020/06/121.12.93.11.02020/09/111.12.11&#…...

linux命令:调试必备工具dmesg
在服务器上进行芯片调试时,我们会遇到各种各样的问题,很多问题与操作系统相关。此时就需要了解操作系统发生了哪些事件。 dmesg 是linux系统中用来打印或控制内核缓冲区内容的命令。这个环形缓冲区记录了系统启动以来发生的各种事件消息,包括…...

第三届大湾区算力大会丨暴雨开启数字未来新篇
5月30-31日,韶关市迎来主题为“算启新篇智创未来”的第三届粤港澳大湾区(广东)算力产业大会暨第二届中国算力网大会,活动由广东省人民政府主办,广东省政数局、韶关市人民政府共同承办。暴雨信息作为算力产业发展的重要构建者受邀赴会…...
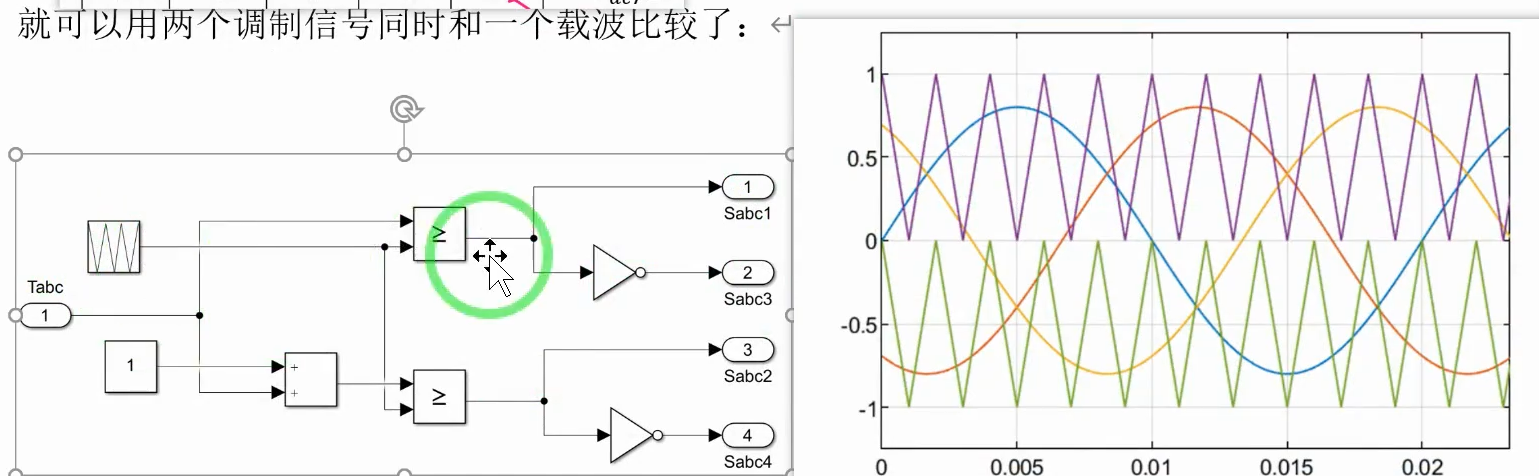
SPWM载波调制方式-三电平杂记1
方法一: P2 O1 N0 方法二:双载波直接发波 方法三:负轴载波和调制波往上抬升1,得到使用同一个载波 在正半周在P和O切换,在下半轴式O和N切换...

常见攻击类型整理
文章目录 网络攻击web攻击XSS攻击存储型XSS反射型XSSDOM型XSS CSRF攻击SQL注入攻击文件上传漏洞业务逻辑漏洞越权访问水平越权垂直越权 密码找回验证码漏洞 信息泄露暴力破解远程命令执行(RCE)xxe注入反序列化文件包含本地文件包含(LFI&#…...

R语言探索与分析-美国房价及其影响因素分析
一、选题背景 以多元线性回归统计模型为基础,用R语言对美国部分地区房价数据进行建模预测,进而探究提高多元回 归线性模型精度的方法。先对数据进行探索性预处理,随后设置虚拟变量并建模得出预测结果,再使用方差膨胀因子对 多重共…...
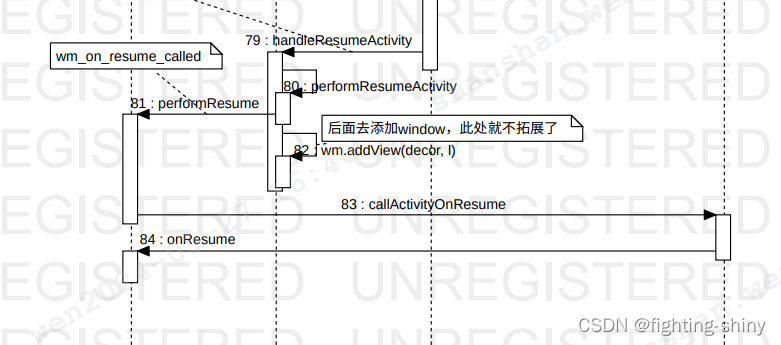
Android14 WMS-窗口添加流程(一)-Client端
窗口布局在onCreate方法中通过setContentView(R.layout.xxx)加载,但窗口的显示并不是在wm_on_create_called中, 而是在wm_on_resume_called后,也就是说应用onResume时此窗口是不可见的,真正可见是当此window窗口的mDrawState变化状态从NO_SUR…...
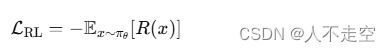
【人工智能】第二部分:ChatGPT的架构设计和训练过程
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...

Informer
I n f o r m e r Informer Informer 摘要: 长序列时间序列的预测 i n f o r m e r informer informer优点: P r o b s p a r e Probspare Probspare自关注机制,在时间复杂度和内存使用方面达到 O ( N l o g N ) O(NlogN) O(NlogN),在序列依…...

12岁学什么编程机构好:深入剖析与全面指导
12岁学什么编程机构好:深入剖析与全面指导 在数字化时代,编程已成为一项必备技能。对于12岁的孩子来说,选择一个合适的编程机构至关重要。然而,市场上的编程机构众多,如何选择成为了一个难题。本文将从四个方面、五个…...

Day60 柱状图中最大的矩形
84 柱状图中最大的矩形 题目链接:84. 柱状图中最大的矩形 - 力扣(LeetCode) 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的…...

typescript --object对象类型
ts中的object const obj new Object()Object 这里的Object是Object类型,而不是JavaScript内置的Object构造函数。 这里的Object是一种类型,而Object()构造函数表示一个值。 Object()构造函数的ts代码 interface ObjectConstructor{readonly prototyp…...

如何使用python将多个EXCEL表进行合并
在Python中,你可以使用pandas库来轻松地将多个Excel表格合并。以下是一个基本的步骤指南和示例代码,说明如何合并多个Excel文件到一个单独的DataFrame中: 步骤 安装pandas和openpyxl(如果你正在处理.xlsx文件)。导入…...

【前端每日基础】day35——HTML5离线存储
HTML5引入了一些新的特性和API来增强Web应用的功能,其中之一就是离线存储。离线存储允许Web应用在没有网络连接的情况下仍能正常运行。以下是HTML5离线存储的主要技术和详细介绍: Web Storage (LocalStorage 和 SessionStorage) LocalStorage 概述&…...

动态规划算法:背包问题
背包问题概述 背包问题 (Knapsack problem) 是⼀种组合优化的 NP完全问题 。 问题可以描述为:给定⼀组物品,每种物品都有⾃⼰的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最⾼。 根据物品的个…...
新版idea配置git步骤及项目导入
目录 git安装 下载 打开git Bash 配置全局用户名及邮箱 查看已经配置的用户名和邮箱 在IDEA中设置Git 问题解决 项目导入 前言-与正文无关 生活远不止眼前的苦劳与奔波,它还充满了无数值得我们去体验和珍惜的美好事物。在这个快节奏的世界中࿰…...
)
赶紧收藏!2024 年最常见 20道 Kafka面试题(一)
一、Kafka都有哪些特点? Kafka是一个分布式流处理平台,它被设计用于高吞吐量的数据管道和流处理。以下是Kafka的一些主要特点: 高吞吐量、低延迟:Kafka每秒可以处理数十万条消息,延迟可以低至几毫秒。这是通过优化数据…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...

第14节 Node.js 全局对象
JavaScript 中有一个特殊的对象,称为全局对象(Global Object),它及其所有属性都可以在程序的任何地方访问,即全局变量。 在浏览器 JavaScript 中,通常 window 是全局对象, 而 Node.js 中的全局…...
