集成算法:Bagging模型、AdaBoost模型和Stacking模型
概述
目的:让机器学习效果更好,单个不行,集成多个
集成算法
Bagging:训练多个分类器取平均
f ( x ) = 1 / M ∑ m = 1 M f m ( x ) f(x)=1/M\sum^M_{m=1}{f_m(x)} f(x)=1/M∑m=1Mfm(x)
Boosting:从弱学习器开始加强,通过加权来进行训练
F m ( x ) = F m − 1 ( x ) + a r g m i n h ∑ i = 1 n L ( y i , F m − 1 ( x i ) + h ( x i ) ) F_m(x)=F_{m-1}(x)+argmin_h\sum^n_{i=1}L(y_i,F_{m-1}(x_i)+h(x_i)) Fm(x)=Fm−1(x)+argminh∑i=1nL(yi,Fm−1(xi)+h(xi))
(加入一棵树,新的树更关注之前错误的例子)
Stacking:聚合多个分类或回归模型(可以分阶段来做)
Bagging模型(随机森林)
全称: bootstrap aggregation(说白了就是并行训练一堆分类器)
最典型的代表就是随机森林,现在Bagging模型基本上也是随机森林。
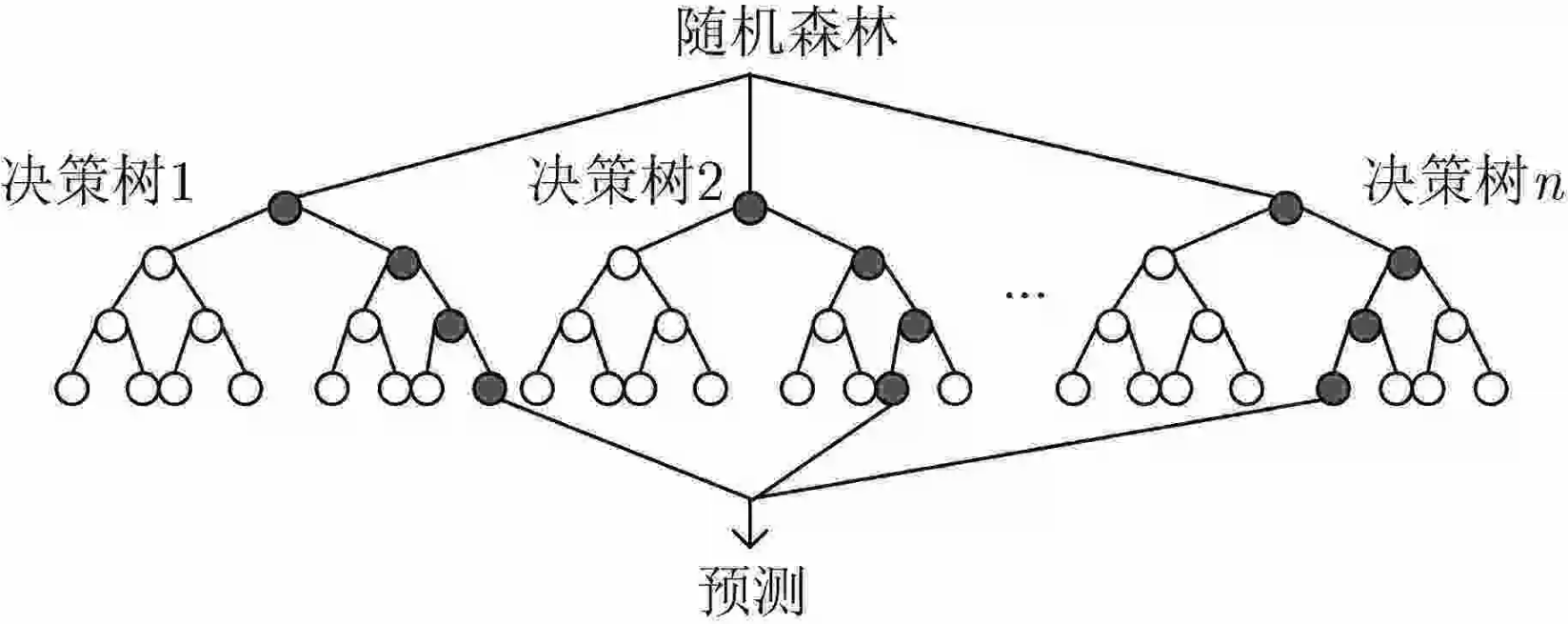
随机:数据采样随机,每棵树只用部分数据;数据有多个特征(属性)组成,每棵树随机选择部分特征。随机是为了使得每个分类器拥有明显差异性。
森林:很多个决策树并行放在一起
如何对所有树选择最终结果?分类的话可以采取少数服从多数,回归的话可以采用取平均值。
构造树模型

由于二重随机性,使得每个树基本上都不会一样,最终的结果也会不一样。
树模型:
随机性
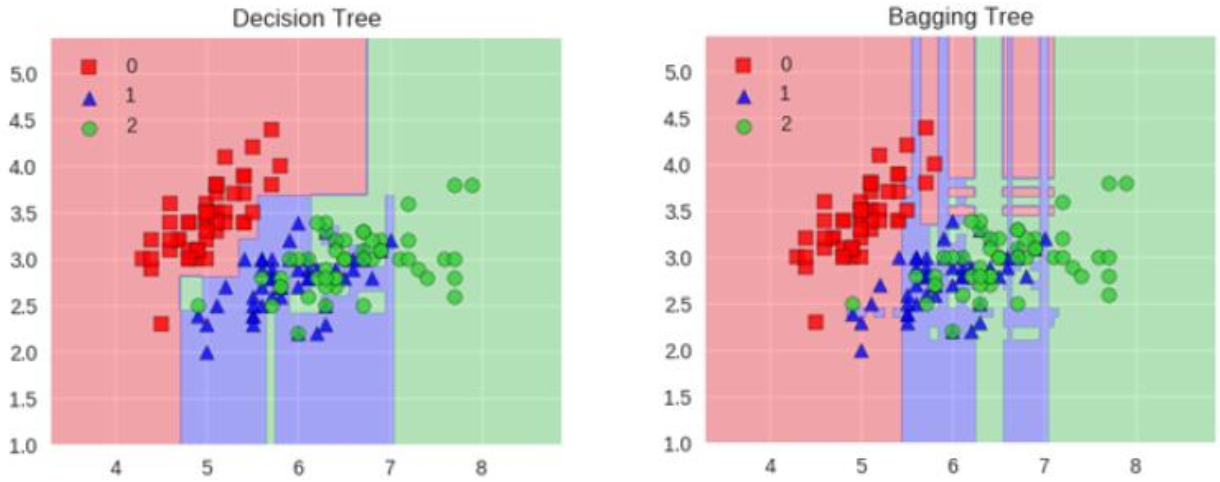
之所以要进行随机,是要保证泛化能力,如果树都一样,那就没意义了!
如下图所示,当每个弱分类器分类错误的样本各不相同时,则能得到一个效果优异的集成模型。
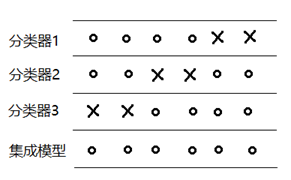
随机森林优势
它能够处理很高维度的数据,即数据拥有很多特征(属性),并且不用做特征选择(集成算法自动选择了重要的特征)。
在训练完后,它能够给出哪些feature比较重要。
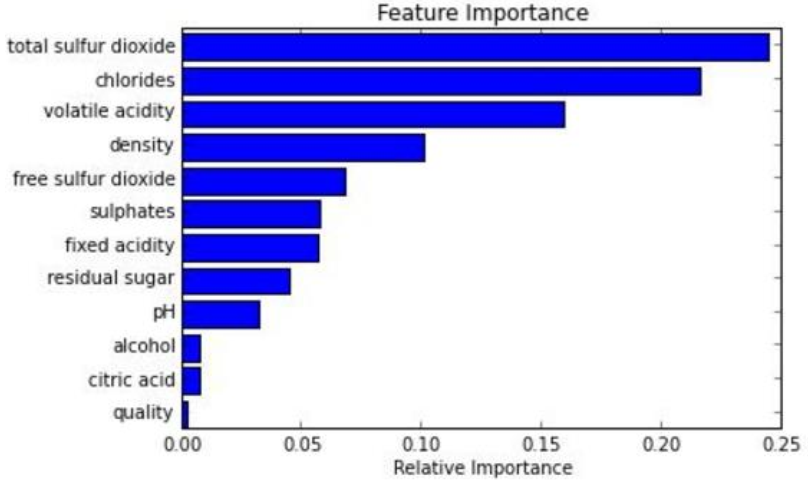
可以进行可视化展示,便于分析。
容易做成并行化方法,速度比较快。
解答:为什么随机森林能够给出哪些feature比较重要。
假如有四个分类器 A , B , C , D A,B,C,D A,B,C,D,他们对应关注(随机选择到)的属性为 a , b , c , d a,b,c,d a,b,c,d
取 A , B , C , D A,B,C,D A,B,C,D的结果并且按少服从多数(也可以去平均等决策策略)得到错误了 e r r o r 1 error_1 error1
之后我们给 B B B制作假数据,把之前真的数据结果打乱或者换成不合理的值,得到 B ′ B' B′,之后
取 A , B ′ , C , D A,B',C,D A,B′,C,D的结果并且按少服从多数(也可以去平均等决策策略)得到错误了 e r r o r 2 error_2 error2
如果 e r r o r 2 ≈ e r r o r 1 error_2\approx error_1 error2≈error1,则说明属性 B B B并不重要。
如果 e r r o r 2 ≫ e r r o r 1 error_2 \gg error_1 error2≫error1,则说明属性 B B B非常重要,对结果造成了巨大影响。
关于树的个数
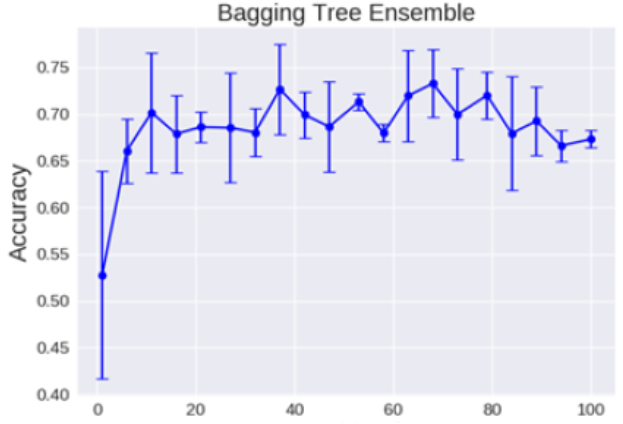
理论上越多的树效果会越好,但实际上基本超过一定数量就差不多上下浮动了。
Boosting模型(提升算法模型)
概述:
F m ( x ) = F m − 1 ( x ) + a r g m i n h ∑ i = 1 n L ( y i , F m − 1 ( x i ) + h ( x i ) ) F_m(x)=F_{m-1}(x)+argmin_h\sum^n_{i=1}L(y_i,F_{m-1}(x_i)+h(x_i)) Fm(x)=Fm−1(x)+argminh∑i=1nL(yi,Fm−1(xi)+h(xi))
假如有三个分类器 A , B , C A,B,C A,B,C,这个时候正如公式所示, A , B , C A,B,C A,B,C有种串联的感觉。
假如有1000条数据, A A A仅分类正确900条,之后 B B B就关注错误的100条数据,仅那100条作为数据预测(这个做法有点极端,也可以拿小部分900条里面的数据),之后 B B B正确预测出50条,那么 C C C就那拿剩下的50条错误的数据用来给 C C C预测。
典型代表: AdaBoost, Xgboost
AdaBoost模型
Adaboost会根据前一次的分类效果调整数据权重,如果某一个数据在这次分错了,那么在下一次我就会给它更大的权重。
最终的结果:每个分类器根据自身的准确性来确定各自的权重,再合并结果。
Adaboost工作流程
每一次切一刀,最终合在一起,弱分类器效果就更好了
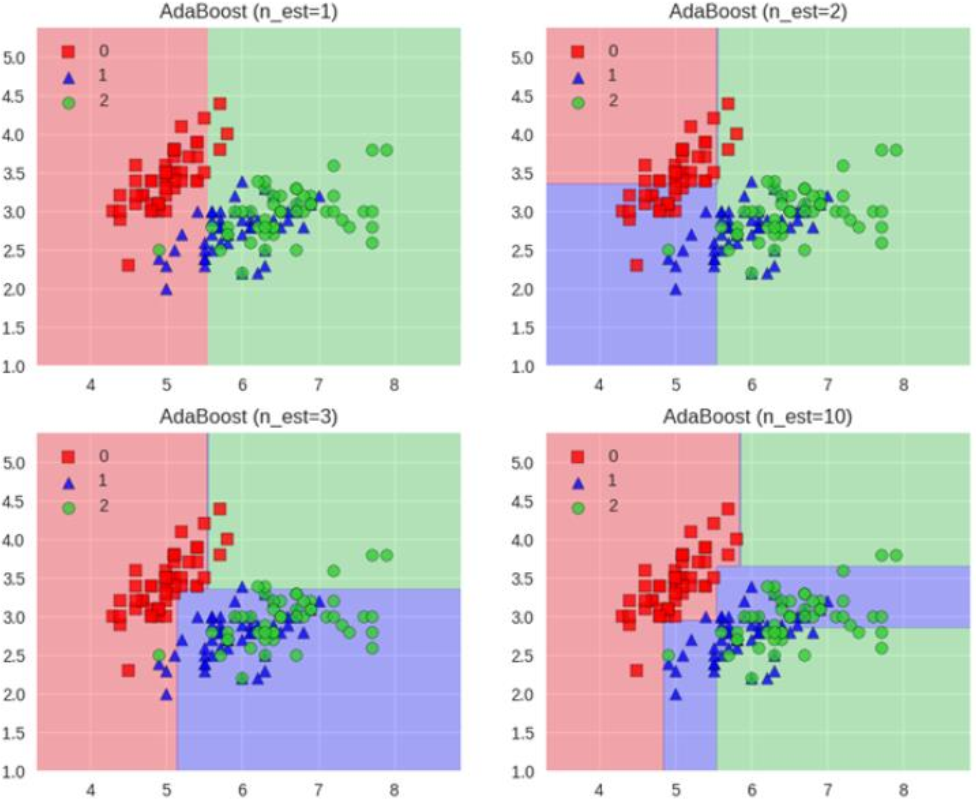
Stacking模型
堆叠:很暴力,拿来一堆分类器直接上
可以堆叠各种各样的分类器( KNN,SVM,RF等等)
为了刷结果,不择手段!
分阶段:第一阶段得出各自结果,第二阶段再用前一阶段结果训练
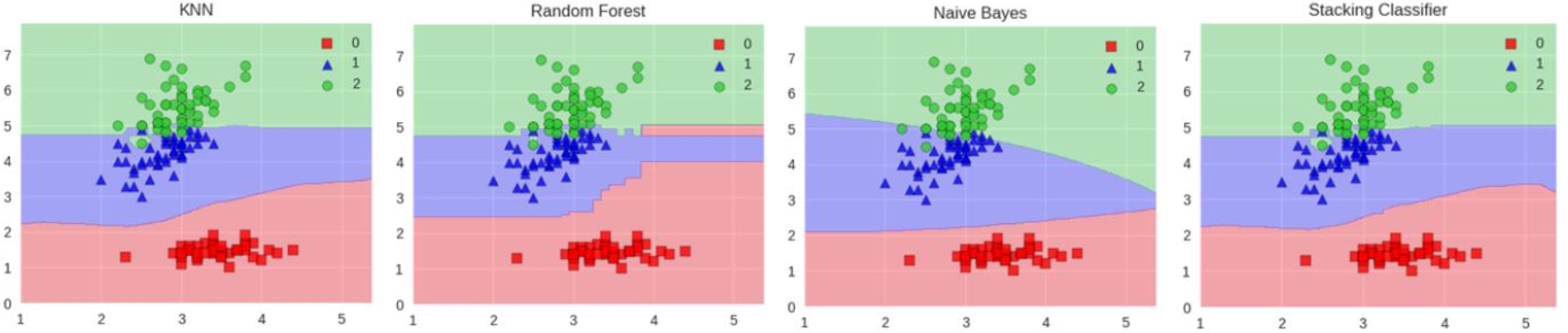
堆叠在一起确实能使得准确率提升,但是速度是个问题。
相关文章:

集成算法:Bagging模型、AdaBoost模型和Stacking模型
概述 目的:让机器学习效果更好,单个不行,集成多个 集成算法 Bagging:训练多个分类器取平均 f ( x ) 1 / M ∑ m 1 M f m ( x ) f(x)1/M\sum^M_{m1}{f_m(x)} f(x)1/M∑m1Mfm(x) Boosting:从弱学习器开始加强&am…...

DW怎么Python:探索Dreamweaver与Python的交织世界
DW怎么Python:探索Dreamweaver与Python的交织世界 在数字世界的广袤天地中,Dreamweaver(简称DW)与Python这两大工具各自闪耀着独特的光芒。DW以其强大的网页设计和开发能力著称,而Python则以其简洁、易读和强大的编程…...

算法(十三)回溯算法---N皇后问题
文章目录 算法概念经典例子 - N皇后问题什么是N皇后问题?实现思路 算法概念 回溯算法是类似枚举的深度优先搜索尝试过程,主要是再搜索尝试中寻找问题的解,当发生不满足求解条件时,就会”回溯“返回(也就是递归返回&am…...
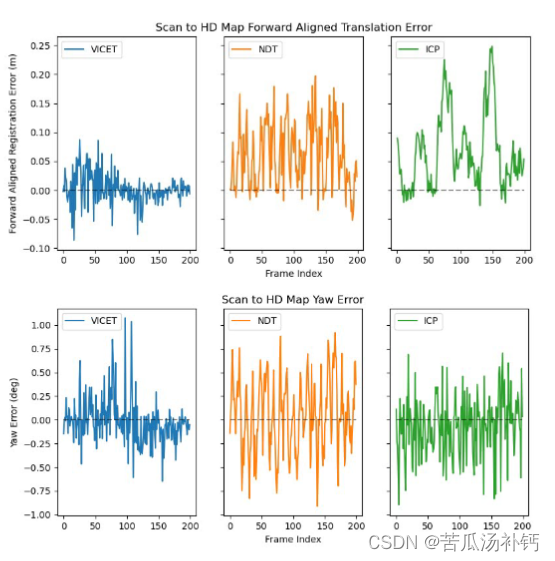
论文阅读:Correcting Motion Distortion for LIDAR HD-Map Localization
目录 概要 Motivation 整体架构流程 技术细节 小结 论文地址:http://arxiv.org/pdf/2308.13694.pdf 代码地址:https://github.com/mcdermatt/VICET 概要 激光雷达的畸变矫正是一个非常重要的工作。由于扫描式激光雷达传感器需要有限的时间来创建…...
Git操作笔记
学git已经好多次了。但是还是会忘记很多的东西,一些常用的操作命令和遇到的bug以后在这边记录汇总下 一.github图片展示 图片挂载,我是创建了一个库专门存图片,然后在github的md中用专用命令展示图片,这样你的md就不会全是文字那…...

使用Python进行数据分析的基本步骤
简介: 在当今的数据驱动世界中,数据分析已成为各行各业不可或缺的一部分。Python作为一种强大的编程语言,提供了丰富的库和工具,使得数据分析变得简单易行。本文将带你了解使用Python进行数据分析的基本步骤。 一、数据获取 从外…...
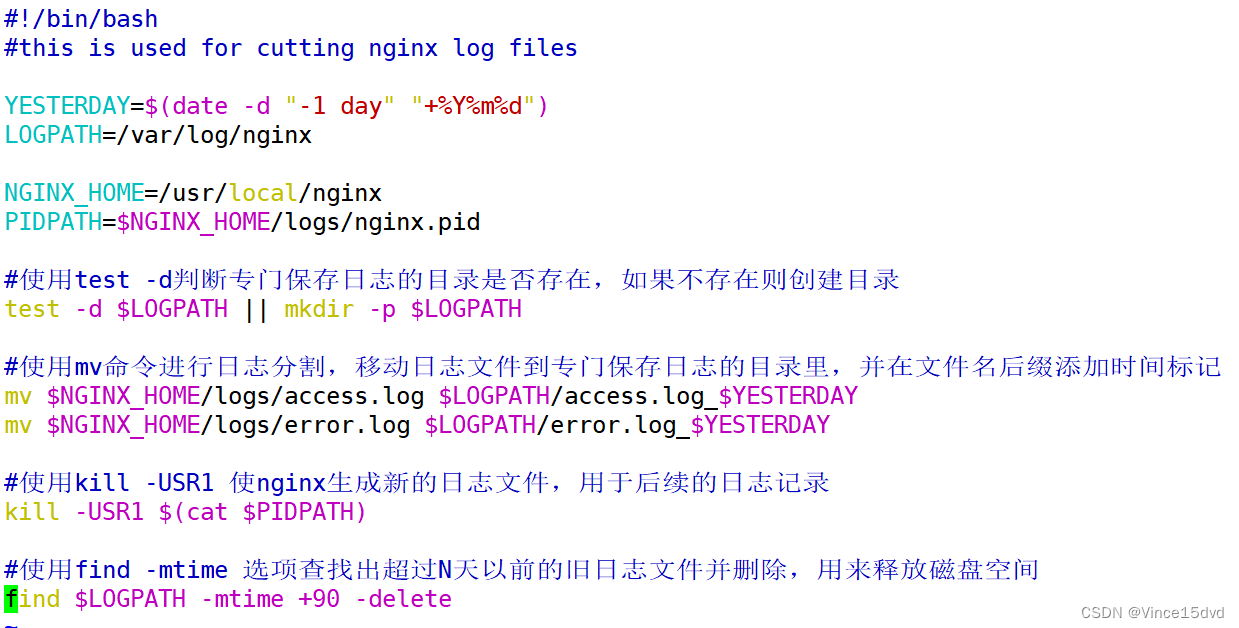
NGINX优化
NGINX优化分为两个方面: 一. nginx应用配置文件的优化: 1.nginx的性能优化: 全局块: 设置工作进程数: work_processes #设置工作进程数 设置工作进程连接数:work_rilmit_nofile #设置每个worker进程最大可…...

【LeetCode刷题】二分查找:山脉数组的峰顶索引、寻找峰值
【LeetCode刷题】Day 13 题目1:852.山脉数组的峰顶索引思路分析:思路1:暴力枚举O(N)思路2:二分查找O(logN) 题目2:162.寻找峰值思路分析:思路1:二分查找O(logN) 题目1:852.山脉数组的…...

《Python学习》-- 实操篇一
一、文件操作 1. 1 读取文本文件 # 文件操作模式 # r (默认) - 只读模式。文件必须存在,否则会抛出FileNotFoundError。在这种模式下,你只能读取文件内容,不能写入或追加。 # w - 写入模式。如果文件存在,内容会被清空ÿ…...
 —— List/Queue类)
C# 集合(二) —— List/Queue类
总目录 C# 语法总目录 集合二 List/Queue 1. List2. Queue 1. List List有ArrayList和LinkedList ArrayList 类似数组,查找快,插入删除慢(相对)LinkedList 类似双向链表,查找慢(相对),插入删除快 //ArrayList //ArrayList Arr…...

【TB作品】MSP430 G2553 单片机口袋板,读取单片机P1.4电压显示,ADC
功能 读取P1.4电压,显示到口袋板显示屏,电压越高亮灯越多。 部分程序 while (1){ADC10CTL0 | ENC ADC10SC; // Sampling and conversion startLPM0;adcvalue ADC10MEM; //原始数据 0到1023adtest (float) adcvalue / 1024.…...

知乎x-zse-96、x-zse-81
声明 本文章中所有内容仅供学习交流使用,不用于其他任何目的,抓包内容、敏感网址、数据接口等均已做脱敏处理,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关!wx a15018601872 本文章未…...

【Linux】Linux工具——yum,vim
1.Linux 软件包管理器——yum Linux安装软件: 源代码安装(不建议)rpm安装(类似Linux安装包,版本可能不兼容,不推荐,容易报错)yum安装(解决了安装源,安装版本&…...
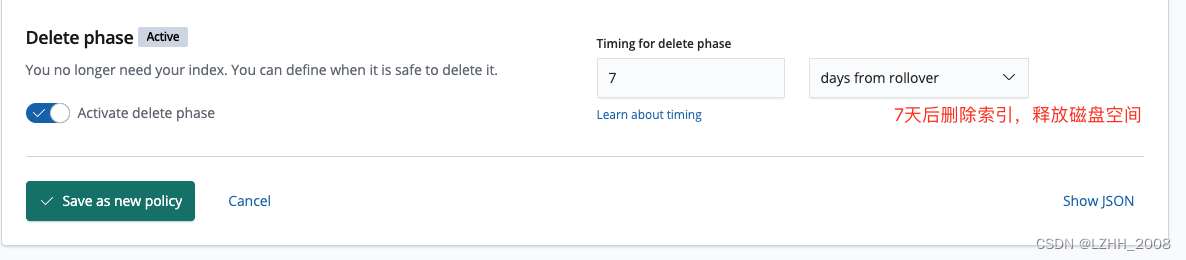
ES 生命周期管理
一 .概念 ILM定义了四个生命周期阶段:Hot:正在积极地更新和查询索引。Warm:不再更新索引,但仍在查询。cold:不再更新索引,很少查询。信息仍然需要可搜索,但是如果这些查询速度较慢也可以。Dele…...

【JavaScript脚本宇宙】揭秘HTTP请求库:深入理解它们的特性与应用
深度揭秘:六大HTTP请求库的比较与应用 前言 在这篇文章中,我们将探讨六种主要的HTTP请求库。这些库为处理网络请求提供了不同的工具和功能,包括Axios、Fetch API、Request、SuperAgent、Got和Node-fetch。通过本文,你将对每个库…...
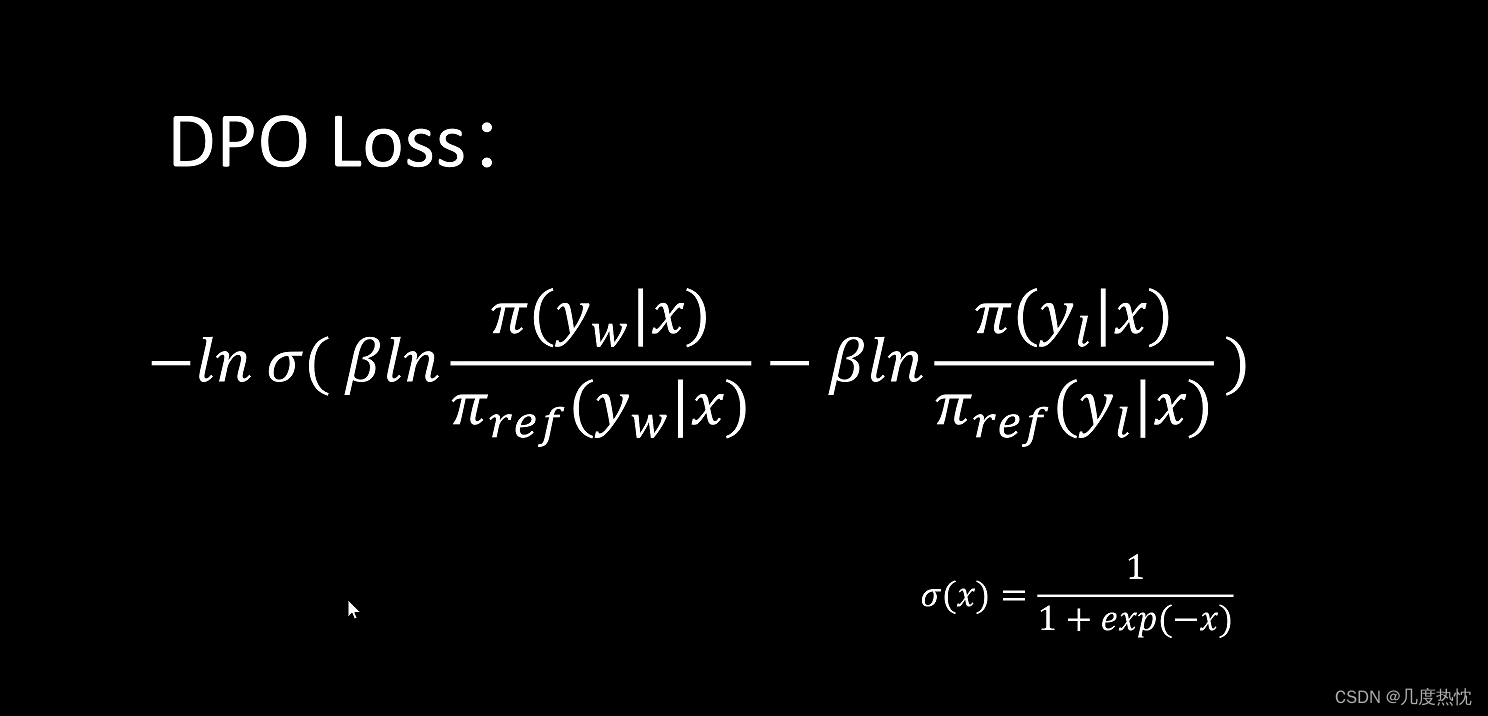
【强化学习】DPO(Direct Preference Optimization)算法学习笔记
【强化学习】DPO(Direct Preference Optimization)算法学习笔记 RLHF与DPO的关系KL散度Bradley-Terry模型DPO算法流程参考文献 RLHF与DPO的关系 DPO(Direct Preference Optimization)和RLHF(Reinforcement Learning f…...

vue3 todolist 简单例子
vue3 简单的TodList 地址: https://gitee.com/cheng_yong_xu/vue3-composition-api-todo-app-my 效果 step-1 初始化项项目 我们不采用vue cli 搭建项目 直接将上图文件夹,复制到vscode编辑器,清空App.vue的内容 安装包 # 安装包 npm…...

Linux项目编程必备武器!
本文目录 一、更换源服务器二、下载man开发手册(一般都自带,没有的话使用下面方法下载) 一、更换源服务器 我们使用apt-get等下载命令下载的软件都是从源服务器上获取的,有些软件包在某个服务器上存在,而另一个服务器不存在。所以我们可以添加…...

AndroidStudio编译很慢问题解决
如果gradle同步、编译下载很慢,可以换一下仓库阿里云镜像 repositories {maven { url https://maven.aliyun.com/repository/google } maven { url https://maven.aliyun.com/repository/jcenter } maven { url https://maven.aliyun.com/repository/public } goog…...
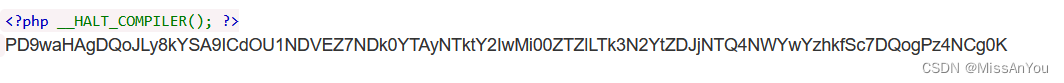
PHAR反序列化
PHAR PHAR(PHP Archive)文件是一种归档文件格式,phar文件本质上是一种压缩文件,会以序列化的形式存储用户自定义的meta-data。当受影响的文件操作函数调用phar文件时,会自动反序列化meta-data内的内容,这里就是我们反序…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...
