【C++杂货铺】unordered系列容器
目录
🌈 前言🌈
📁 unordered系列关联式容器
📁 底层结构
📂 哈希概念
📂 哈希冲突
📂 哈希函数
📂 哈希冲突解决
📁 模拟实现
📁 总结
🌈 前言🌈
欢迎收看本期【C++杂货铺】,本期内容将讲解C++的STL中的unordered系列容器,其中包含了unordered_map 和 unordered_set 的使用,底层结构哈希的原理,实现,最后模拟实现unordered系列的容器。
📁 unordered系列关联式容器
在C++98中,STL提供了底层为红黑树结构的系列关联式容器,在查询时效率可达到 O(log2),即最差情况下需要比较红黑树的高度次,当书中的节点比较多时,查询效率也不理想。
最好的查询是,进行很少的比较次数就能将元素找到,因此在C++11中,STL又提供了4个unordered系列的关联式容器,这四个容器与红黑树结构的关联式容器使用方式基本类似,只是底层结构不同,本文中只对unordered_map 和 unordered_set进行介绍。
其中,unordered_map是存储 <key , value>键值对的关联式容器,其允许通过key快速的索引找到对应的value。
📁 底层结构
unordered系列的关联式容器效率之所以比较高,是因为底层使用了哈希结构。
📂 哈希概念
顺序结构及平衡树中,元素关键码与其存储位置之间没有对应关系,因此在查找一个元素时,必须要经过关键码的多次比较。顺序查找时间复杂度为O(N) ,平衡术中为树的高度,即O(logN),搜索效率取决于搜索过程中元素的比较次数。
理想的搜索方法是:可以不经过任何比较,一次直接从表中得到搜索的元素。如果构造一种存储结构,通过某种函数(HashFunc)使得元素的存储位置和它的关键码之间能够建立一种映射关系,那么在查找时通过该函数可以很快找到该元素。
该结构中:
● 插入元素:根据插入元素的关键码,用哈希函数计算出该元素的存储位置并按次位置进行存放。
● 搜搜元素:对元素的关键码进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按次位置取元素的比较,若关键码相等,则搜索成功。
该方式即为哈希(散列)方法,哈希方法中使用的转换函数称为哈希(散列)函数,构造出的结构为哈希表(散列表)。
该方法不必经过多次关键码的比较,因此搜索的速度比较快。
📂 哈希冲突
当两个数据元素的关键码 i != j , 但是Hash(i) == Hash(j),即:不同关键码通过相同的哈希函数计算出相同的哈希地址,这种现象成为哈希冲突(哈希碰撞)。
📂 哈希函数
引起哈希冲突的一个原因可能是,哈希函数设计不合理。
哈希函数的设计原则:
1. 哈希函数的定义域必须包括需要存储的全部关键码,如果散列表允许有m个地址,其值域必须在0 ~ m-1 之间。
2. 哈希函数计算出的地址能均匀分布在整个空间中
3. 哈希函数应比较简单。
常见的哈希函数:
1. 直接定址法(常用)
取关键字的某个线性函数为散列地址:Hash(key) = A*Key + B。
优点:简单,均匀
缺点:需要实现知道关键字的分布情况
使用场景:适合查找比较小且连续的情况
2. 除留余数法(常用)
设散列表允许的地址数为m,取一个不大于m,但是接近或等于m的质数p作为除数,按照哈希函数:Hash(key) = key % p (p <= m) ,将关键字改为哈希地址。
3. 平方取中法
假设关键字为1234,对它平方就是1522756,抽取中间的3位227作为哈希地址;
再比如关键字为4321,对它平方就是18671041,抽取中间的3位671(或710)作为哈希地址
平方取中法比较适合:不知道关键字的分布,而位数又不是很大的情况
4. 折叠法(了解)
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些),然后将这 几部分叠加求和,并按散列表表长,取后几位作为散列地址。
折叠法适合事先不需要知道关键字的分布,适合关键字位数比较多的情况
5. 随机数法(了解)
选择一个随机函数,取关键字的随机函数值为它的哈希地址,即H(key) = random(key),其中 random为随机数函数。
通常应用于关键字长度不等时采用此法。
6. 数学分析法(了解)
设有n个d位数,每一位可能有r种不同的符号,这r种不同的符号在各位上出现的频率不一定 相同,可能在某些位上分布比较均匀,每种符号出现的机会均等,在某些位上分布不均匀只 有某几种符号经常出现。可根据散列表的大小,选择其中各种符号分布均匀的若干位作为散 列地址。例如:
假设要存储某家公司员工登记表,如果用手机号作为关键字,那么极有可能前7位都是 相同 的,那么我们可以选择后面的四位作为散列地址,如果这样的抽取工作还容易出现 冲突,还 可以对抽取出来的数字进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环移 位、前两数与后两数叠加(如1234改成12+34=46)等方法。
数字分析法通常适合处理关键字位数比较大的情况,如果事先知道关键字的分布且关键字的 若干位分布较均匀的情况
注意:哈希函数设计的越精妙,产生哈希冲突的可能性就越低,但是无法避免哈希冲突
📂 哈希冲突解决
1. 闭散列
闭散列也叫做开放定址法,当发生哈希冲突时,如果哈希表未被填满,说明在哈希表中必然还有空位置,那么可以吧key存放到冲突位置的“下一个”空位置中区。那么如果寻找下一个空位置呢?
1.1 线性探测:从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止。
插入:
● 通过哈希函数获取插入元素在哈希表中的位置
● 如果该位置中没有元素啧直接插入新元素,如果该位置中有元素发生哈希冲突,使用线性探测找到下一个空位置,插入新元素。

删除:
采用闭散列处理哈希冲突时,不能随便物理删除哈希表中已有的元素,若直接删除元素会影响到其他元素的搜索。比如函数元素4,如果直接删除,44差啊后起来会受到影响。因此线性探测采用标记的未删除法来删除掉一个元素。
// 哈希表每个空间给个标记
// EMPTY此位置空, EXIST此位置已经有元素, DELETE元素已经删除
enum State{EMPTY, EXIST, DELETE};
// 注意:假如实现的哈希表中元素唯一,即key相同的元素不再进行插入
// 为了实现简单,此哈希表中我们将比较直接与元素绑定在一起
template<class K, class V>
class HashTable
{struct Elem{ pair<K, V> _val;State _state;};public:HashTable(size_t capacity = 3): _ht(capacity), _size(0){for(size_t i = 0; i < capacity; ++i)_ht[i]._state = EMPTY;}bool Insert(const pair<K, V>& val){// 检测哈希表底层空间是否充足// _CheckCapacity();size_t hashAddr = HashFunc(key);// size_t startAddr = hashAddr;while(_ht[hashAddr]._state != EMPTY){if(_ht[hashAddr]._state == EXIST && _ht[hashAddr]._val.first
== key)return false;hashAddr++;if(hashAddr == _ht.capacity())hashAddr = 0;/*// 转一圈也没有找到,注意:动态哈希表,该种情况可以不用考虑,哈希表中元
素个数到达一定的数量,哈希冲突概率会增大,需要扩容来降低哈希冲突,因此哈希表中元素是
不会存满的if(hashAddr == startAddr)return false;*/}// 插入元素_ht[hashAddr]._state = EXIST;_ht[hashAddr]._val = val;_size++;return true;}int Find(const K& key){size_t hashAddr = HashFunc(key);while(_ht[hashAddr]._state != EMPTY){if(_ht[hashAddr]._state == EXIST && _ht[hashAddr]._val.first
== key)return hashAddr;hashAddr++;}return hashAddr;}bool Erase(const K& key){int index = Find(key);if(-1 != index){_ht[index]._state = DELETE;_size++;return true;}return false;}size_t Size()const;bool Empty() const; void Swap(HashTable<K, V, HF>& ht);
private:size_t HashFunc(const K& key){return key % _ht.capacity();}
private:vector<Elem> _ht;size_t _size;
};
思考:哈希表什么情况下进行扩容?如何扩容?

void CheckCapacity()
{if(_size * 10 / _ht.capacity() >= 7){HashTable<K, V, HF> newHt(GetNextPrime(ht.capacity));for(size_t i = 0; i < _ht.capacity(); ++i){if(_ht[i]._state == EXIST)newHt.Insert(_ht[i]._val);}Swap(newHt);}
}线性探测优点:实现非常简单
线性探测缺点:一旦发生哈希冲突,所有的冲突连载一起,容易产生数据堆积,即:不同关键码占据了可利用的空位置,使得寻找某关键码的位置需要许多次比较,导致搜搜效率降低,如何缓解呢?
1.2 二次探测
线性探测的缺陷是产生冲突的数据堆积在一起,这与其找下一个空位置有关系,因为找空位置的方式就是挨着往后逐个去找,因此二次探测是为了避免该问题。
找到下一个空位置的方法为:H(i) = (k + i^2) % m 或者 H(i) = (k - i^2) % m,其中i = 1,2,3..,k是通过哈希函数,对元素键值key进行计算得到的地址,m是表的大小。
研究表明:当表的长度为质数且表装载因子a不超过0.5时,新的表项一定能够插入,而且任 何一个位置都不会被探查两次。因此只要表中有一半的空位置,就不会存在表满的问题。在 搜索时可以不考虑表装满的情况,但在插入时必须确保表的装载因子a不超过0.5,如果超出 必须考虑增容。
因此,闭散列最大的缺陷就是空间利用率较低,这也是哈希的缺陷。
2. 开散列
开散列又叫做链地址发(开链法),首先要对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于一个集合,每一个子集和称为一个桶,各个桶中的元素通过一个单链表链接起来,各个链表的头节点存储在哈希表中。

template<class V>
struct HashBucketNode
{HashBucketNode(const V& data): _pNext(nullptr), _data(data){}HashBucketNode<V>* _pNext;V _data;
};
// 本文所实现的哈希桶中key是唯一的
template<class V>
class HashBucket
{typedef HashBucketNode<V> Node;typedef Node* PNode;
public:HashBucket(size_t capacity = 3): _size(0){ _ht.resize(GetNextPrime(capacity), nullptr);}// 哈希桶中的元素不能重复PNode* Insert(const V& data){// 确认是否需要扩容。。。 // _CheckCapacity();// 1. 计算元素所在的桶号size_t bucketNo = HashFunc(data);// 2. 检测该元素是否在桶中PNode pCur = _ht[bucketNo];while(pCur){if(pCur->_data == data)return pCur;pCur = pCur->_pNext;}// 3. 插入新元素pCur = new Node(data);pCur->_pNext = _ht[bucketNo];_ht[bucketNo] = pCur;_size++;return pCur;}// 删除哈希桶中为data的元素(data不会重复),返回删除元素的下一个节点PNode* Erase(const V& data){size_t bucketNo = HashFunc(data);PNode pCur = _ht[bucketNo];PNode pPrev = nullptr, pRet = nullptr;while(pCur){if(pCur->_data == data){if(pCur == _ht[bucketNo])_ht[bucketNo] = pCur->_pNext;elsepPrev->_pNext = pCur->_pNext;pRet = pCur->_pNext;delete pCur;_size--;return pRet;}}return nullptr;}PNode* Find(const V& data);size_t Size()const;bool Empty()const;void Clear();bool BucketCount()const;void Swap(HashBucket<V, HF>& ht;~HashBucket();
private:size_t HashFunc(const V& data){return data%_ht.capacity();}
private:vector<PNode*> _ht;size_t _size; // 哈希表中有效元素的个数
};开散列增容:
桶的个数是一定的,随着元素的不断插入,每个桶中元素的个数不断增多,极端情况下,可 能会导致一个桶中链表节点非常多,会影响的哈希表的性能,因此在一定条件下需要对哈希 表进行增容,那该条件怎么确认呢?开散列最好的情况是:每个哈希桶中刚好挂一个节点, 再继续插入元素时,每一次都会发生哈希冲突,因此,在元素个数刚好等于桶的个数时,可 以给哈希表增容。
void _CheckCapacity()
{size_t bucketCount = BucketCount();if(_size == bucketCount){HashBucket<V, HF> newHt(bucketCount);for(size_t bucketIdx = 0; bucketIdx < bucketCount; ++bucketIdx){PNode pCur = _ht[bucketIdx];while(pCur){// 将该节点从原哈希表中拆出来_ht[bucketIdx] = pCur->_pNext;// 将该节点插入到新哈希表中size_t bucketNo = newHt.HashFunc(pCur->_data);pCur->_pNext = newHt._ht[bucketNo];newHt._ht[bucketNo] = pCur;pCur = _ht[bucketIdx];}}newHt._size = _size;this->Swap(newHt);}
}
📁 模拟实现
1. 模拟实现哈希表
template<class T>
struct HashNode
{HashNode(){}HashNode(const T& data):_data(data), _next(nullptr){}T _data;HashNode* _next;
};template<class K,class T,class KOfT ,class Hash=HashFunc<K>>
class HashTable
{typedef HashNode<T> Node;public:template<class Ptr,class Ref>struct HashTableIterator{typedef HashNode<T> Node;typedef HashTableIterator Self;Node* _node = nullptr;const HashTable* _pht;HashTableIterator(Node* node, const HashTable* pht):_node(node), _pht(pht){}Self& operator++(){KOfT kot;Hash hs;if (_node->_next == nullptr){size_t hashi = hs(kot(_node->_data)) % _pht->_tables.size();hashi++;for (; hashi < _pht->_tables.size();hashi++){if (_pht->_tables[hashi] != nullptr){break;}}if (hashi == _pht->_tables.size()){_node = nullptr;}else{_node = _pht->_tables[hashi];}}else{_node = _node->_next;}return *this;}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}bool operator!=(const Self& it){return _node != it._node;}};typedef HashTableIterator<T*, T&> Iterator;typedef HashTableIterator<const T*, const T&> const_Iterator;HashTable(){_tables.resize(10,nullptr);_n = 0;}Iterator Begin(){//this -> HT*Node* cur = nullptr;for (int i = 0; i < _tables.size();i++){if (_tables[i]){cur = _tables[i];break;}}return Iterator(cur, this);}Iterator End(){//this -> HT*return Iterator(nullptr,this);}const_Iterator Begin() const{//this -> const HT*Node* cur = nullptr;for (int i = 0; i < _tables.size();i++){if (_tables[i]){cur = _tables[i];break;}}return const_Iterator(cur, this);}const_Iterator End() const{//this -> const HT*return const_Iterator(nullptr, this);}Iterator Find(const K& k){Hash hs;KOfT kot;size_t hashi = hs(k) % _tables.size();Node* cur = _tables[hashi];while (cur){if (kot(cur->_data) == k)return Iterator(cur, this);cur = cur->_next;}return Iterator(nullptr, this);}pair<Iterator,bool> Insert(const T& data){Hash hs;KOfT kot;Iterator it = Find(kot(data));if (it != End())return make_pair(it, false);if (_n == _tables.size()){//扩容vector<Node*> newtables(_tables.size() * 2,nullptr);for (int i = 0; i < _tables.size(); i++){if (_tables[i]){Node* cur = _tables[i];while (cur){size_t hashi = hs(kot(cur->_data)) % newtables.size();Node* next = cur->_next;cur->_next = newtables[i];newtables[hashi] = cur;cur = next;}}}_tables.swap(newtables);}size_t hashi = hs(kot(data)) % _tables.size();Node* newnode = new Node(data);newnode->_next = _tables[hashi];_tables[hashi] = newnode;_n++;return make_pair(Iterator(_tables[hashi], this),true);}bool Erase(const K& k){if (Find(k) == nullptr)return false;Hash hs;KOfT kot;size_t hashi = hs(k) % _tables.size();Node* prev = nullptr;Node* cur = _tables[hashi];while (cur){if (kot(cur->_data) == k){if (prev == nullptr){_tables[hashi] = cur->_next;}else{prev->_next = cur->_next;}delete cur;break;}prev = cur;cur = cur->_next;}return true;}private:vector<Node*> _tables;size_t _n = 0;
};2. 模拟实现unordered_set
template<class K>
class unordered_set
{struct SetKOfT{K operator()(const K& key){return key;}};public:typedef typename hash_bucket::HashTable<K, K, SetKOfT>::Iterator iterator;typedef typename hash_bucket::HashTable<K, K, SetKOfT>::const_Iterator const_iterator;pair<iterator, bool> insert(const K& key){return ht.Insert(key);}bool erase(const K& key){return ht.Erase(key);}iterator find(const K& key){return ht.Find(key);}iterator begin(){return ht.Begin();}iterator end(){return ht.End();}const_iterator begin() const{return ht.Begin();}const_iterator end() const{return ht.End();}private:hash_bucket::HashTable<K, K,SetKOfT> ht;
};3. 模拟实现unordered_map
template<class K, class V>
class unordered_map
{struct MapKOfT{K operator()(const pair<K, V>& kv){return kv.first;}};public:typedef typename hash_bucket::HashTable<K, pair<K, V>, MapKOfT>::Iterator iterator;typedef typename hash_bucket::HashTable<K, pair<K, V>, MapKOfT>::const_Iterator const_iterator;iterator insert(const pair<K, V>& kv){return ht.Insert(kv);}bool erase(const K& key){return ht.Erase(key);}iterator find(const K& key){return ht.Find(key);}iterator begin(){return ht.Begin();}iterator end(){return ht.End();}const_iterator begin() const{return ht.Begin();}const_iterator end() const{return ht.End();}V& operator[](const K& key){pair<iterator, bool> ret = ht.Insert(make_pair(key, V()));return ret.first->second;}private:hash_bucket::HashTable<K, pair<K,V>,MapKOfT> ht;
};📁 总结
以上,就是本期内容,介绍了unordered_set 和 unordered_map是什么,底层的哈希表,什么是哈希,以及哈希实现快速查找的原理,通过某种哈希函数对关键字进行计算,得到地址。也讲解了如果不同值计算得到相同地址,即哈希冲突时,如何处理。
最后,也给出了模拟实现哈希表,unordered_set 和 unordered_map的代码。

相关文章:

【C++杂货铺】unordered系列容器
目录 🌈 前言🌈 📁 unordered系列关联式容器 📁 底层结构 📂 哈希概念 📂 哈希冲突 📂 哈希函数 📂 哈希冲突解决 📁 模拟实现 📁 总结 🌈 前…...
模板-初阶
引言: 在C,我们已经学过了函数重载,这使得同名函数具有多个功能。但是还有一种更省力的方法:采用模板。 本文主要介绍以下内容 1. 泛型编程 2. 函数模板 3. 类模板 1.泛型编程 在将这一部分之前,通过一个故事引…...

重载运算符C++---学习笔记
一、笔记 1. 重载运算符基础知识 重载运算符进行的运算和普通数的加减运算不同之处在于重载运算符的操作数为一个一个自定义的对象,所以相应的要对普通的运算符如-*%/的调用方法进行重写,重载的本质还是函数调用 2. 重载运算符的语法 重载运算符的语…...

SpringMVC枚举类型字段处理
在日常的项目开发中经常会遇到一些取值范围固定的字段,例如性别、证件类型、会员等级等,此时我们可以利用枚举来最大程度减少字段的乱定义,统一管理枚举的值。 SpringMVC中对于枚举也有默认的处理策略: 对于RequestParam…...
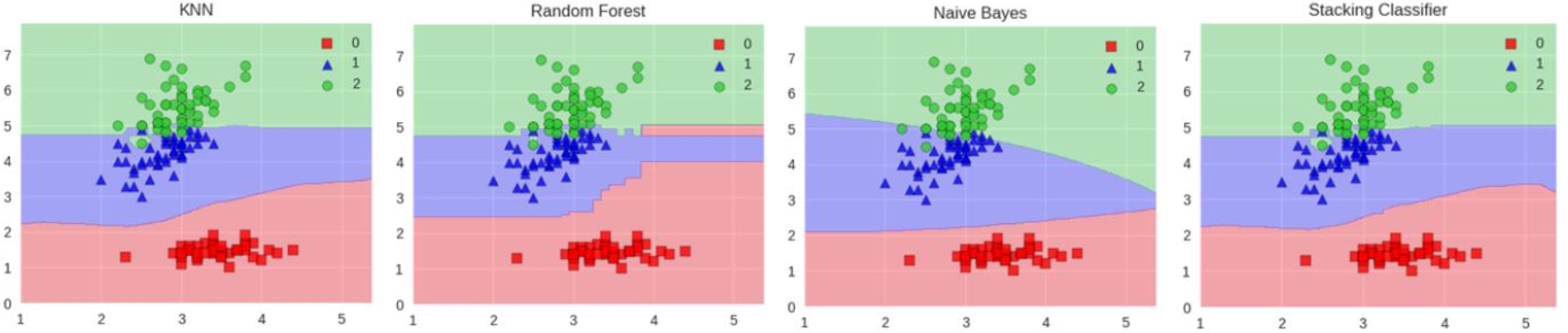
集成算法:Bagging模型、AdaBoost模型和Stacking模型
概述 目的:让机器学习效果更好,单个不行,集成多个 集成算法 Bagging:训练多个分类器取平均 f ( x ) 1 / M ∑ m 1 M f m ( x ) f(x)1/M\sum^M_{m1}{f_m(x)} f(x)1/M∑m1Mfm(x) Boosting:从弱学习器开始加强&am…...

DW怎么Python:探索Dreamweaver与Python的交织世界
DW怎么Python:探索Dreamweaver与Python的交织世界 在数字世界的广袤天地中,Dreamweaver(简称DW)与Python这两大工具各自闪耀着独特的光芒。DW以其强大的网页设计和开发能力著称,而Python则以其简洁、易读和强大的编程…...

算法(十三)回溯算法---N皇后问题
文章目录 算法概念经典例子 - N皇后问题什么是N皇后问题?实现思路 算法概念 回溯算法是类似枚举的深度优先搜索尝试过程,主要是再搜索尝试中寻找问题的解,当发生不满足求解条件时,就会”回溯“返回(也就是递归返回&am…...
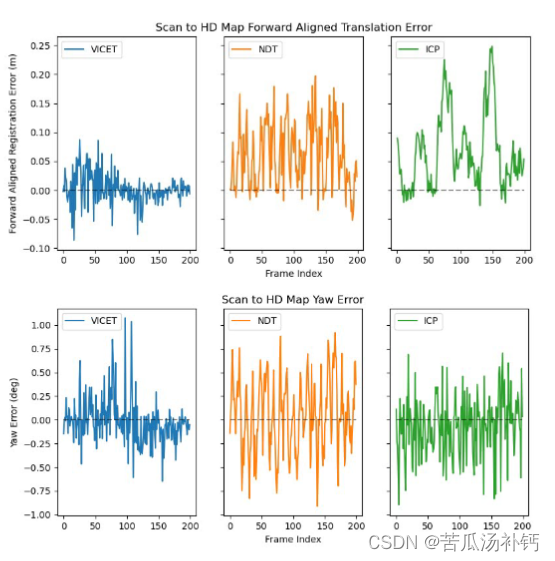
论文阅读:Correcting Motion Distortion for LIDAR HD-Map Localization
目录 概要 Motivation 整体架构流程 技术细节 小结 论文地址:http://arxiv.org/pdf/2308.13694.pdf 代码地址:https://github.com/mcdermatt/VICET 概要 激光雷达的畸变矫正是一个非常重要的工作。由于扫描式激光雷达传感器需要有限的时间来创建…...
Git操作笔记
学git已经好多次了。但是还是会忘记很多的东西,一些常用的操作命令和遇到的bug以后在这边记录汇总下 一.github图片展示 图片挂载,我是创建了一个库专门存图片,然后在github的md中用专用命令展示图片,这样你的md就不会全是文字那…...

使用Python进行数据分析的基本步骤
简介: 在当今的数据驱动世界中,数据分析已成为各行各业不可或缺的一部分。Python作为一种强大的编程语言,提供了丰富的库和工具,使得数据分析变得简单易行。本文将带你了解使用Python进行数据分析的基本步骤。 一、数据获取 从外…...
NGINX优化
NGINX优化分为两个方面: 一. nginx应用配置文件的优化: 1.nginx的性能优化: 全局块: 设置工作进程数: work_processes #设置工作进程数 设置工作进程连接数:work_rilmit_nofile #设置每个worker进程最大可…...

【LeetCode刷题】二分查找:山脉数组的峰顶索引、寻找峰值
【LeetCode刷题】Day 13 题目1:852.山脉数组的峰顶索引思路分析:思路1:暴力枚举O(N)思路2:二分查找O(logN) 题目2:162.寻找峰值思路分析:思路1:二分查找O(logN) 题目1:852.山脉数组的…...

《Python学习》-- 实操篇一
一、文件操作 1. 1 读取文本文件 # 文件操作模式 # r (默认) - 只读模式。文件必须存在,否则会抛出FileNotFoundError。在这种模式下,你只能读取文件内容,不能写入或追加。 # w - 写入模式。如果文件存在,内容会被清空ÿ…...
 —— List/Queue类)
C# 集合(二) —— List/Queue类
总目录 C# 语法总目录 集合二 List/Queue 1. List2. Queue 1. List List有ArrayList和LinkedList ArrayList 类似数组,查找快,插入删除慢(相对)LinkedList 类似双向链表,查找慢(相对),插入删除快 //ArrayList //ArrayList Arr…...

【TB作品】MSP430 G2553 单片机口袋板,读取单片机P1.4电压显示,ADC
功能 读取P1.4电压,显示到口袋板显示屏,电压越高亮灯越多。 部分程序 while (1){ADC10CTL0 | ENC ADC10SC; // Sampling and conversion startLPM0;adcvalue ADC10MEM; //原始数据 0到1023adtest (float) adcvalue / 1024.…...

知乎x-zse-96、x-zse-81
声明 本文章中所有内容仅供学习交流使用,不用于其他任何目的,抓包内容、敏感网址、数据接口等均已做脱敏处理,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关!wx a15018601872 本文章未…...

【Linux】Linux工具——yum,vim
1.Linux 软件包管理器——yum Linux安装软件: 源代码安装(不建议)rpm安装(类似Linux安装包,版本可能不兼容,不推荐,容易报错)yum安装(解决了安装源,安装版本&…...
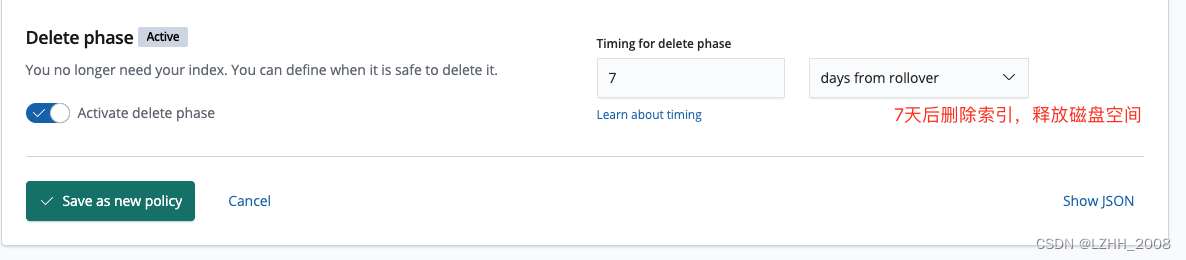
ES 生命周期管理
一 .概念 ILM定义了四个生命周期阶段:Hot:正在积极地更新和查询索引。Warm:不再更新索引,但仍在查询。cold:不再更新索引,很少查询。信息仍然需要可搜索,但是如果这些查询速度较慢也可以。Dele…...

【JavaScript脚本宇宙】揭秘HTTP请求库:深入理解它们的特性与应用
深度揭秘:六大HTTP请求库的比较与应用 前言 在这篇文章中,我们将探讨六种主要的HTTP请求库。这些库为处理网络请求提供了不同的工具和功能,包括Axios、Fetch API、Request、SuperAgent、Got和Node-fetch。通过本文,你将对每个库…...
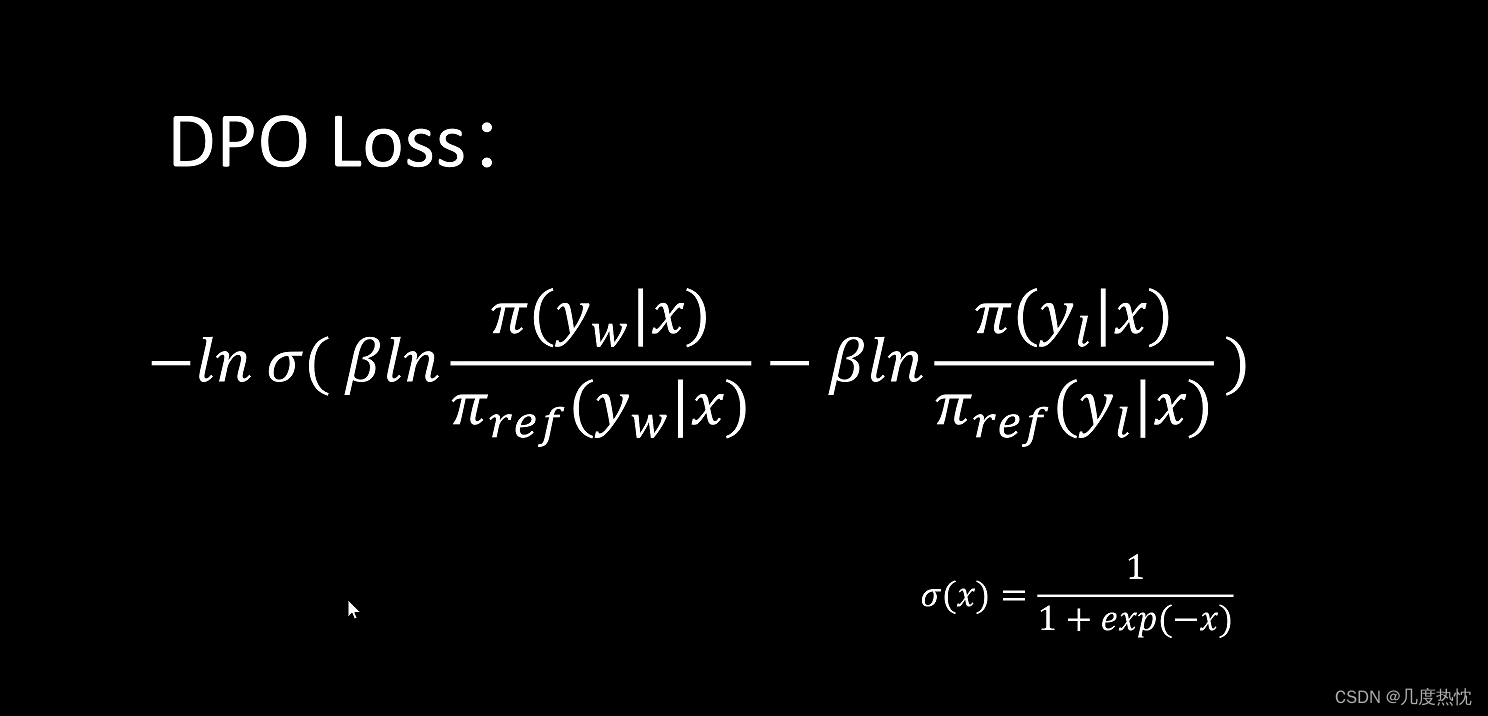
【强化学习】DPO(Direct Preference Optimization)算法学习笔记
【强化学习】DPO(Direct Preference Optimization)算法学习笔记 RLHF与DPO的关系KL散度Bradley-Terry模型DPO算法流程参考文献 RLHF与DPO的关系 DPO(Direct Preference Optimization)和RLHF(Reinforcement Learning f…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

CentOS 7.9安装Nginx1.24.0时报 checking for LuaJIT 2.x ... not found
Nginx1.24编译时,报LuaJIT2.x错误, configuring additional modules adding module in /www/server/nginx/src/ngx_devel_kit ngx_devel_kit was configured adding module in /www/server/nginx/src/lua_nginx_module checking for LuaJIT 2.x ... not…...


