排序-插入排序与选择排序
插入排序
基本思想
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
打扑克牌整理手牌用的就是插入排序的思想

代码实现
void InsertSort(int* a, int n)
{
assert(a);
for (int i = 0; i < n - 1; i++)//将一个数组中所有元素升序
{ //,这里必须是n-1,不然后面数组会越界
int end=i;
int x=a[end+1];//x始终指向end下一个位置的值
while (end >= 0)//每趟插入最多挪动end-1个数据
{
if (a[end] > x)//x前一个数大于x,就将数据往后移一格
{
a[end + 1] = a[end];//这里数组的值会往后覆盖
//但是没关系,我们已经将a[end+1]的值保存在x当中了
end--;
}
else
{
break;//跳出里面的while循环
}
}
a[end + 1] = x;
}
}
特性总结
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
选择排序
基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
就像小学生排队一样,让最矮的那个站到第一排,然后让第二矮的占到第二排,以此类推
代码实现
void SelectSort(int* a, int n)
{
int begain = 0;
int end = n - 1;
while (begain < end)
{
int maxi = begain;//初始化最值
int mini = begain;
for (int i = begain; i <= end; i++)
{
if (a[i] < a[mini])
{
mini = i;//记录下标,否则会有数据被覆盖的问题
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
swap(&a[begain], &a[mini]);//将最大最小值交换
swap(&a[end], &a[maxi]);
begain++;//数组范围往中间缩小
end--;
}
}
代码优化
上述思想是单向的,我们可以让最高的和最矮的同时排序,就可以优化一下,实现双向排序
void SelectSort(int* a, int n)
{
int begain = 0;
int end = n - 1;
while (begain < end)
{
int maxi = begain;
int mini = begain;
for (int i = begain; i <=end; i++)
{
if (a[i] < a[mini])
{
mini = i;//记录下标,否则会有数据被覆盖的问题
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
swap(&a[begain], &a[mini]);
if (maxi == begain)//当最大值为begain时,交换最小值和开头元素后,maxi指向的值不再是最大值了.
{
maxi = mini;
}
swap(&a[end], &a[maxi]);
begain++;
end--;
}
}
特性总结
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
相关文章:

排序-插入排序与选择排序
插入排序 基本思想 把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。 打扑克牌整理手牌用的就是插入排序的思想 代码实现 void InsertSort(int* a, int n) { assert(a); …...

【前端每日基础】day33——响应式布局
响应式布局是一种网页设计的方法,它可以使网站在不同的设备上(如桌面电脑、平板电脑、手机等)以及不同的屏幕尺寸上呈现出最佳的显示效果。响应式布局的目标是使用户在任何设备上都能够方便地访问和浏览网站,而不需要使用不同版本…...
)
leetcode 2981.找出出现至少三次的最长子特殊字符串(纯哈希表暴力)
leetcode 2981.找出出现至少三次的最长子特殊字符串(传送门) class Solution { public:int maximumLength(string s) {int hash[30][52] { 0 },len 1,maxn0;char last A;for (char ch : s) {if (ch last) len;else len 1;for (int i len; i > …...
集成算法实验与分析(软投票与硬投票)
概述 目的:让机器学习效果更好,单个不行,集成多个 集成算法 Bagging:训练多个分类器取平均 f ( x ) 1 / M ∑ m 1 M f m ( x ) f(x)1/M\sum^M_{m1}{f_m(x)} f(x)1/M∑m1Mfm(x) Boosting:从弱学习器开始加强&am…...

网络数据库后端框架相关面试题
面试是工作的第一步,面试中面试官所提出的问题千奇百怪,其中关于网络数据库后端框架面试题汇总如下: 1,关系型数据库和非关系型数据库的区别 关系型数据库主要有 MYsql Iracle SQLSever等 相对于非关系型数据库的优势为查询效率…...
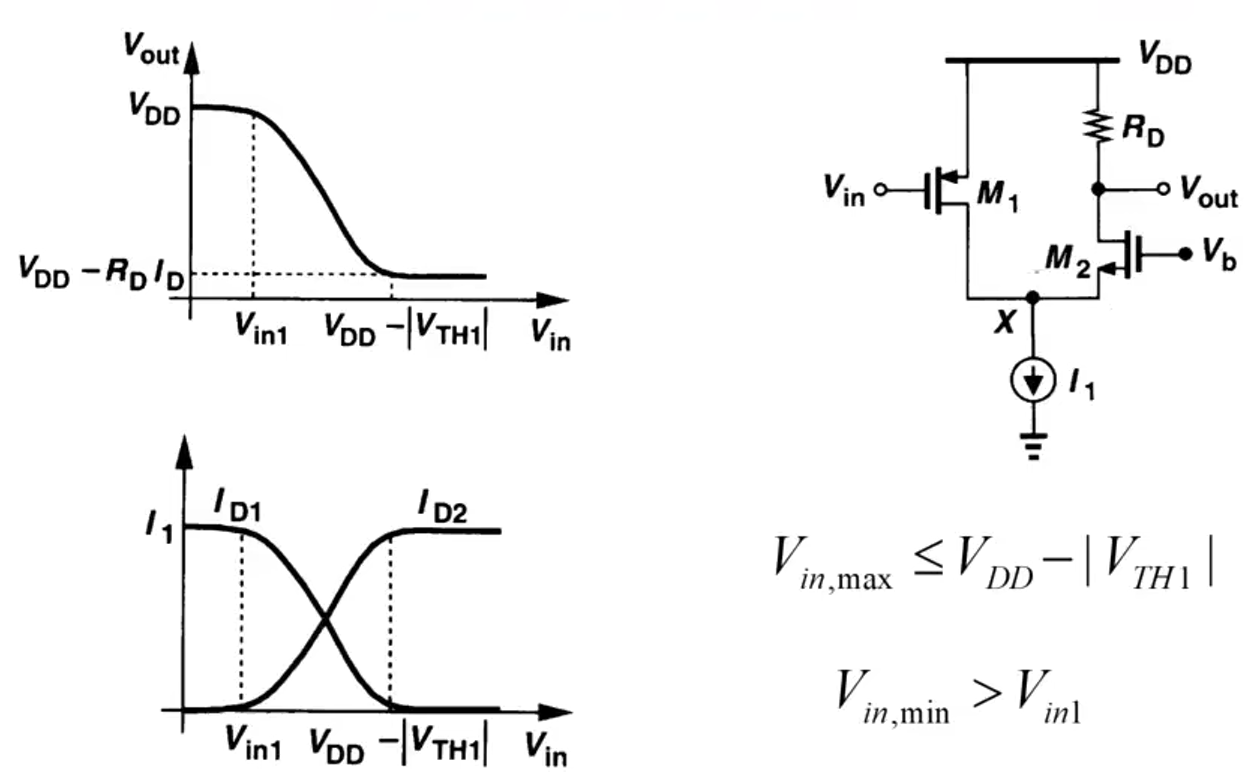
模拟集成电路(6)----单级放大器(共源共栅级 Cascode Stage)
模拟集成电路(6)----单级放大器(共源共栅级 Cascode Stage) 大信号分析 对M1 V x ≥ V i n − V T H 1 V x V B − V G S 2 V B ≥ V i n − V T H 1 V G S 2 V_{x}\geq V_{in}-V_{TH1}\quad V_{x}V_{B}-V_{GS2}\\V_{B}\geq V_{in}-V_{TH1}V_{GS2} Vx…...
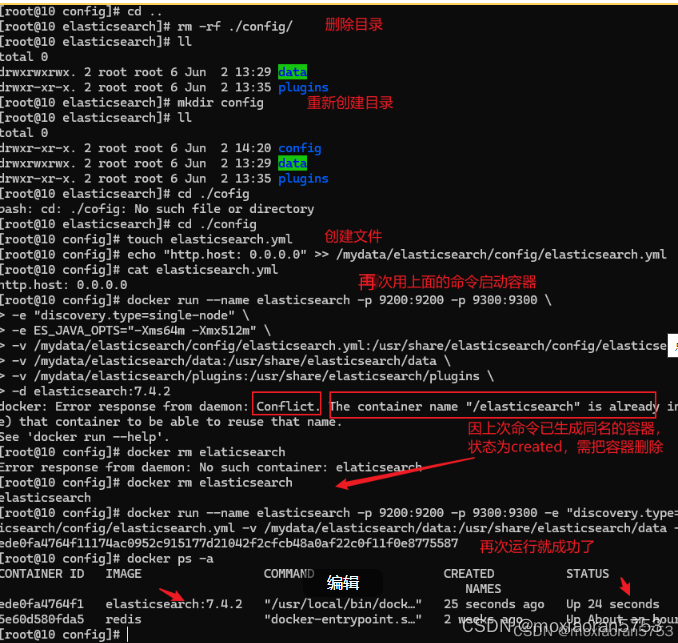
docker以挂载目录启动容器报错问题的解决
拉取镜像: docker pull elasticsearch:7.4.2 docker pull kibana:7.4.2 创建实例: mkdir -p /mydata/elasticsearch/configmkdir -p /mydata/elasticsearch/dataecho "http.host: 0.0.0.0" >> /mydata/elasticsearch/config/elasti…...
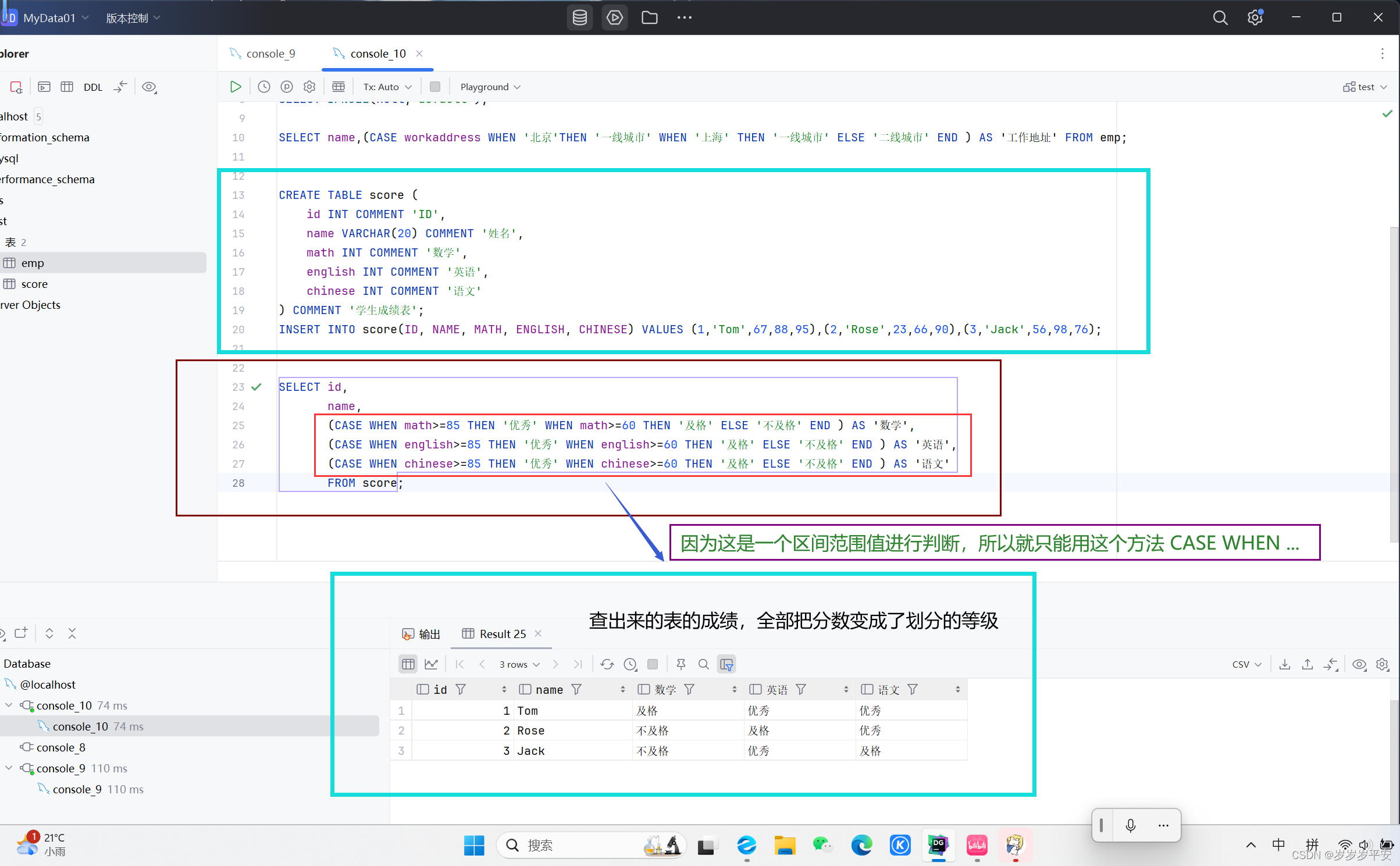
MySQL—函数—流程控制函数(基础)
一、引言 接下来,我们就进入函数的最后一个部分:流程函数。而流程控制函数在我们的日常开发过程是很有用的。 流程控制函数在我们 sql 语句当中,经常用来实现条件的筛选,从而提高语句的一个执行效率。 我们主要介绍以下4个流程控…...
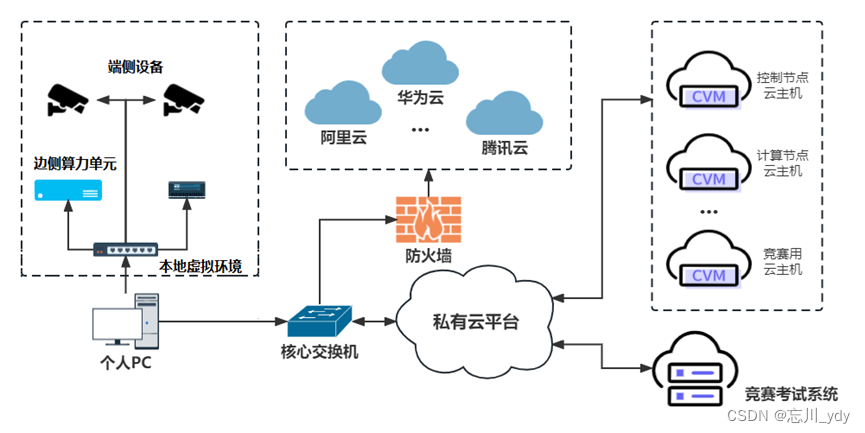
2023年全国职业院校技能大赛(高职组)“云计算应用”赛项赛卷7(私有云)
#需要资源(软件包及镜像)或有问题的,可私聊博主!!! #需要资源(软件包及镜像)或有问题的,可私聊博主!!! #需要资源(软件包…...
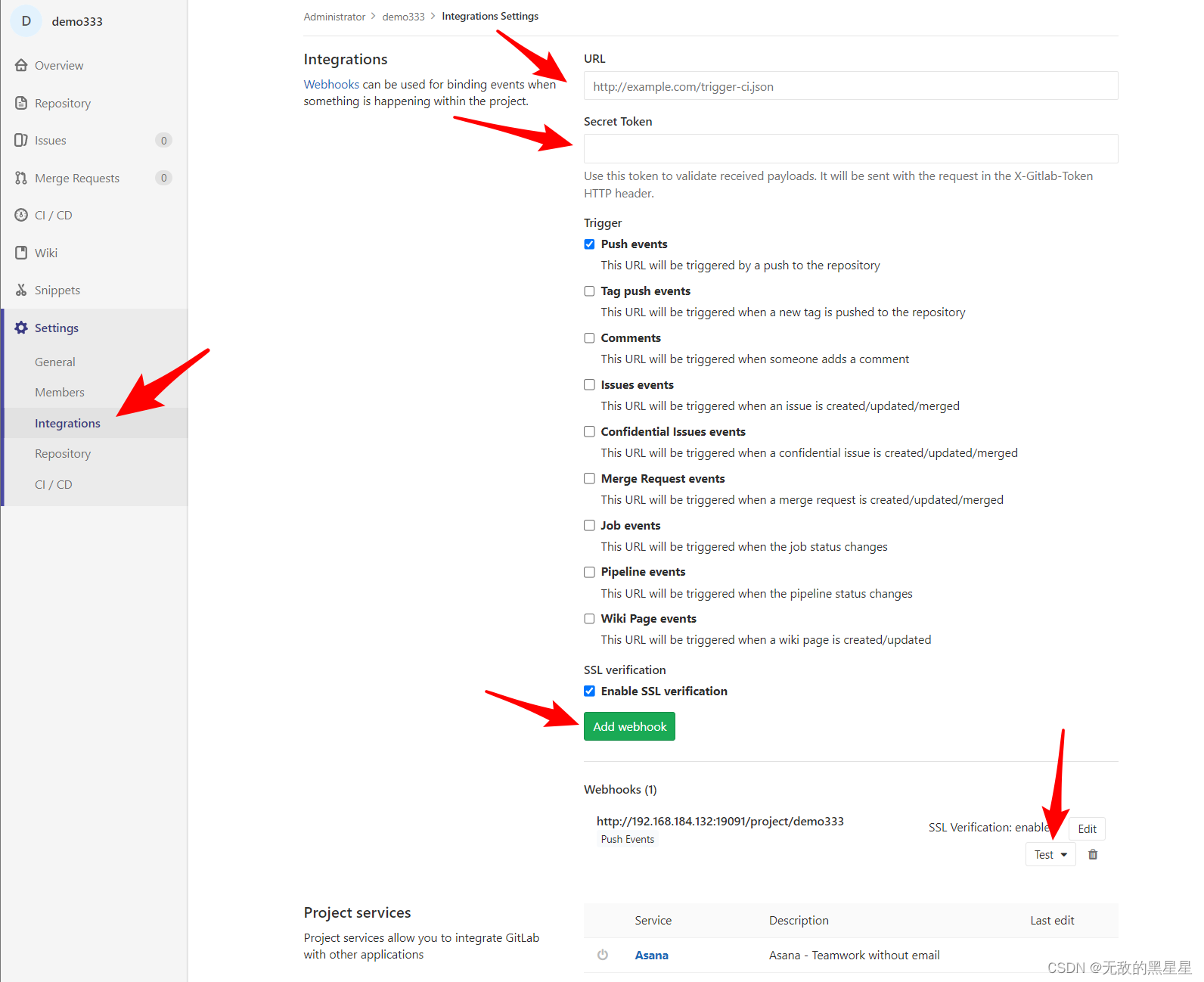
Jenkins、GitLab部署项目
1、安装JDK 1.1、下载openJdk11 yum -y install fontconfig java-11-openjdk1.2、查看安装的版本号 java -version1.3、配置环境变量 vim /etc/profile在最底部添加即可 export JAVA_HOME/usr/lib/jvm/java-11-openjdk-11.0.23.0.9-2.el7_9.x86_64 export PATH$JAVA_HOME/…...
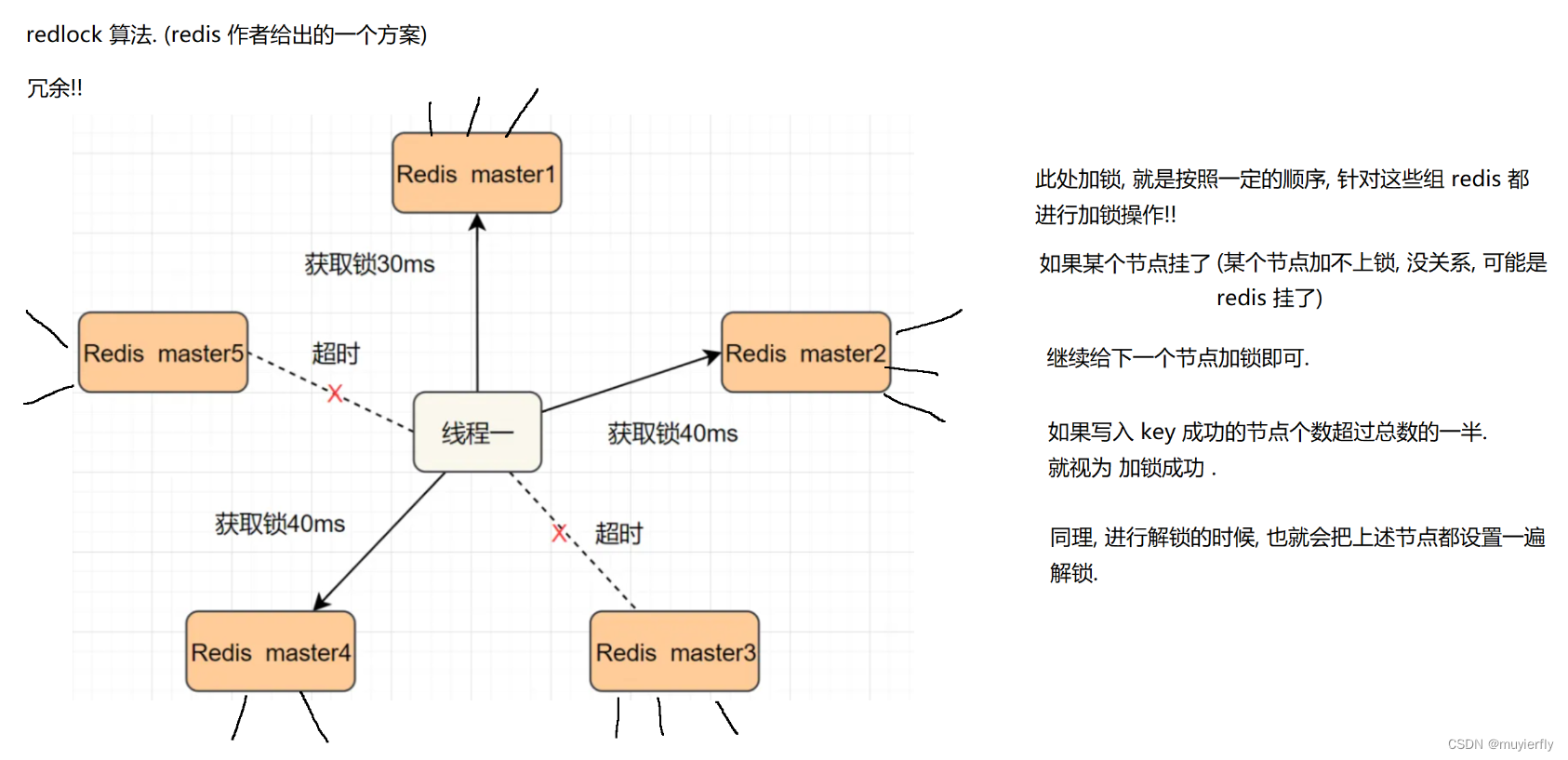
21.Redis之分布式锁
1.什么是分布式锁 在⼀个分布式的系统中, 也会涉及到多个节点访问同⼀个公共资源的情况. 此时就需要通过 锁 来做互斥控制, 避免出现类似于 "线程安全" 的问题. ⽽ java 的 synchronized 或者 C 的 std::mutex, 这样的锁都是只能在当前进程中⽣效, 在分布式的这种多…...

Mysql基础学习:mysql8 JSON字段查询操作
文章目录 一、查询JSON中某个属性值为XXX的数据量1、方式一2、方式二 二、查询的JSON中的value并去除双引号 一、查询JSON中某个属性值为XXX的数据量 1、方式一 select count(*)from table_namewhere JSON_CONTAINS(json-> $.filed1, "xxx")or JSON_CONTAINS(jso…...

搭建基于Django的博客系统数据库迁移从Sqlite3到MySQL(四)
上一篇:搭建基于Django的博客系统增加广告轮播图(三) 下一篇:基于Django的博客系统之用HayStack连接elasticsearch增加搜索功能(五) Sqlite3数据库迁移到MySQL 数据库 迁移原因 Django 的内置数据库 SQL…...

24年护网工具,今年想参加护网的同学要会用
24年护网工具集 吉祥学安全知识星球🔗http://mp.weixin.qq.com/s?__bizMzkwNjY1Mzc0Nw&mid2247483727&idx1&sndb05d8c1115a4539716eddd9fde4e5c9&chksmc0e47813f793f105017fb8551c9b996dc7782987e19efb166ab665f44ca6d900210e6c4c0281&scene21…...
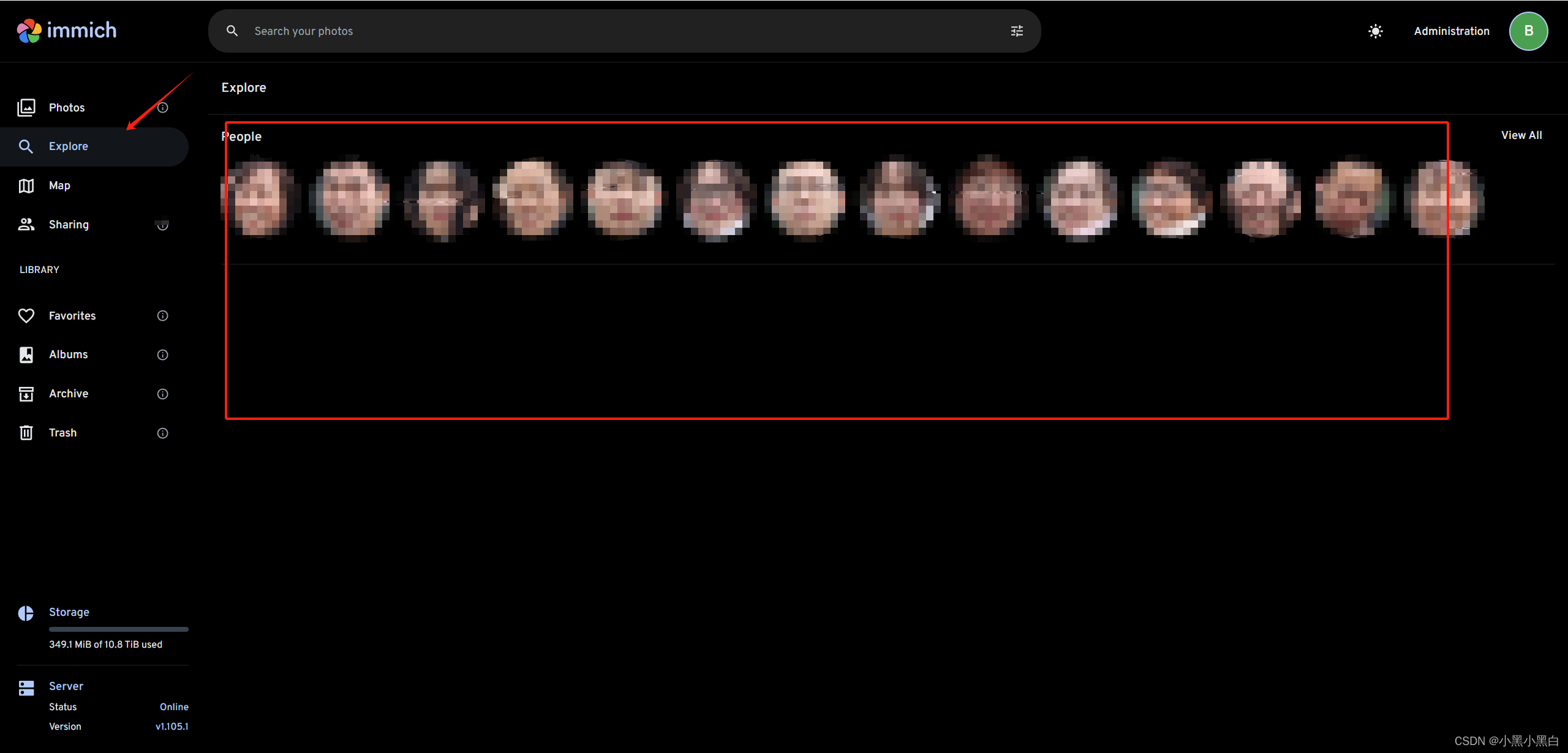
解决TrueNas Scale部署immich后人脸识别失败,后台模型下载异常,immich更换支持中文搜索的CLIP大模型
这个问题搞了我几天终于解决了,搜遍网上基本没有详细针对TrueNas Scale部署immich应用后,CLIP模型镜像下载超时导致人脸识别失败,以及更换支持中文识别的CLIP模型的博客。 分析 现象:TrueNas Scale安装immich官方镜像应用后&…...

面试高频问题----2
一、进程、线程、协程有什么区别? 1.进程:进程是操作系统中独立运行的程序实例,每个进程都有自己的内存空间和系统资源;进程之间相互独立,每个进程有自己的内存地址空间,一个进程无法直接访问另一个进程的…...

Nginx的配置文件-详细使用说明
Nginx的配置文件是Nginx服务器运行的核心,它决定了Nginx如何响应和处理各种请求。以下是对Nginx配置文件(通常名为nginx.conf)的详细解析,按照常见的结构和配置项进行分类: 1. 全局块 user:指定Nginx运行的用户和用户组。例如:user nginx;worker_processes:指定工作进…...

YOLOv5改进 | 卷积模块 | 提高网络的灵活性和表征能力的动态卷积【附代码+小白可上手】
💡💡💡本专栏所有程序均经过测试,可成功执行💡💡💡 轻量级卷积神经网络由于其低计算预算限制了CNNs的深度(卷积层数)和宽度(通道数),…...

23、linux系统文件和日志分析
linux文件系统与日志分析 文件时存储在硬盘上的,硬盘上的最小存储单位是扇区,每个扇区大大小是512字节。 inode:元信息(文件的属性 权限,创建者,创建日期等) block:块,…...
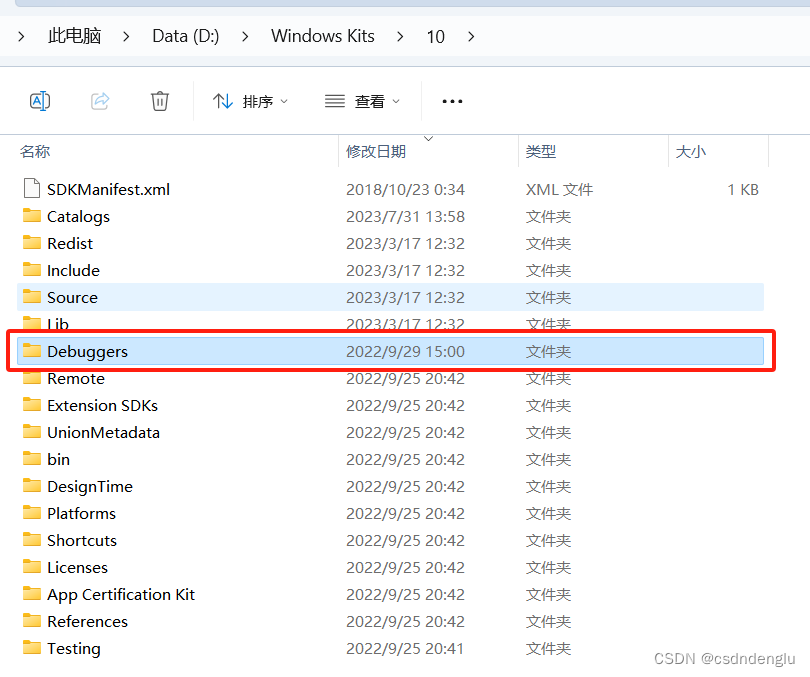
安装VS2017后,离线安装Debugging Tools for Windows(QT5.9.2使用MSVC2017 64bit编译器)
1、背景 安装VS2017后,Windows Software Development Kit - Windows 10.0.17763.132的Debugging Tools for Windows默认不会安装,如下图。这时在QT5.9.2无法使用MSVC2017 64bit编译器。 2、在线安装 如果在线安装参考之前的文章: Qt5.9.2初…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
