【数据结构】链式二叉树详解

个人主页~
链式二叉树基本内容~
链式二叉树详解
- 1、通过前序遍历的数组来构建二叉树
- 2、二叉树的销毁
- 3、二叉树节点个数
- 4、二叉树叶子节点个数
- 5、二叉树第k层节点个数
- 6、二叉树查找
- 7、前序遍历
- 8、中序遍历
- 9、后序遍历
- 10、层序遍历与检查二叉树是否为完全二叉树
- Queue.h
- Queue.c
- 层序遍历代码
- 完全二叉树判断
整个链式二叉树以递归定义为主,需要详细了解递归的相关概念:递归定义在第六条
最需要记住的是:递归定义中的return是退出到上一级,而不是整个程序
1、通过前序遍历的数组来构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a,int n, int* pi)
{if (*pi >= n || a[*pi] == '#'){ // 如果到达数组末尾或遇到#,则返回NULL (*pi)++;//移动到下一个数据return NULL;}BTNode* node = BuyNode(a[*pi]);(*pi)++; // 移动到下一个数据node->left = BinaryTreeCreate(a, n, pi); // 递归创建左子树 node->right = BinaryTreeCreate(a, n, pi); // 递归创建右子树 return node;
}
建树过程(部分过程省略):






2、二叉树的销毁
二叉树销毁是不能够从第一层开始销毁的,这样我们不能销毁所有的节点,从叶节点开始销毁,递归释放,才能销毁二叉树所有节点
void BinaryTreeDestory(BTNode* root)
{if (root == NULL)return;BinaryTreeDestory(root->left);//找到底层左节点BinaryTreeDestory(root->right);//找完左节点找右节点free(root);
}
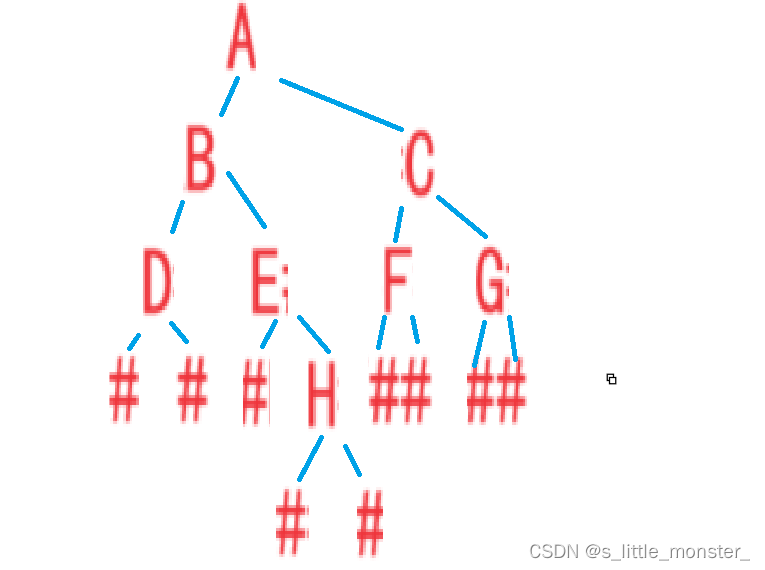
找到D的左子结点,是#返回,再找D的右节点,是#返回,然后释放掉D节点,此时B的root->left结束,进行root->right,以此类推,这样会从最底下的叶节点开始将所有节点释放
3、二叉树节点个数
int BinaryTreeSize(BTNode* root)
{//return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;if (root == NULL)return 0;return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
两种表达方式,一种是普通表达,另一种是三目表达
如果当前节点为空,返回0,如果左右子节点都遍历完了,将结果+1返回
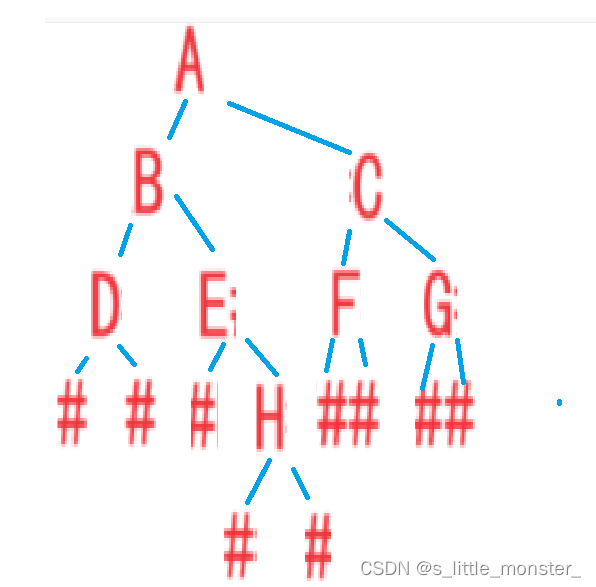
递归走到D的左子结点,返回到D,return 0
右子节点,返回到D,return 0
函数走完返回到B,return 0+0+1
以此类推
4、二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
当前节点为空时,返回0
当前节点不为空且左右子节点都为空时,说明该节点为叶节点,返回1
将左子树的叶节点与右子树的叶节点相加就是二叉树总共的叶子结点个数
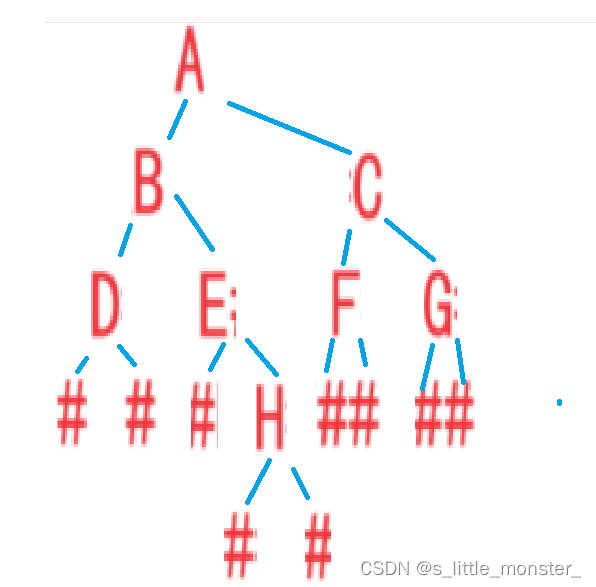
A走到B,B走到D,D的左右节点都为空,D是叶子结点,返回1,返回到B
再走E的左子结点,为空,返回0,走E节点,E节点的左右子节点为空,为叶子节点返回1,以此类推
5、二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
当节点为0时,返回0
当k为1时,只有根节点,返回1
每次递归会使k减1,到第k层时k=1,然后就开始返回,这样递归的定义可以保证第k层的所有个数都可以算到
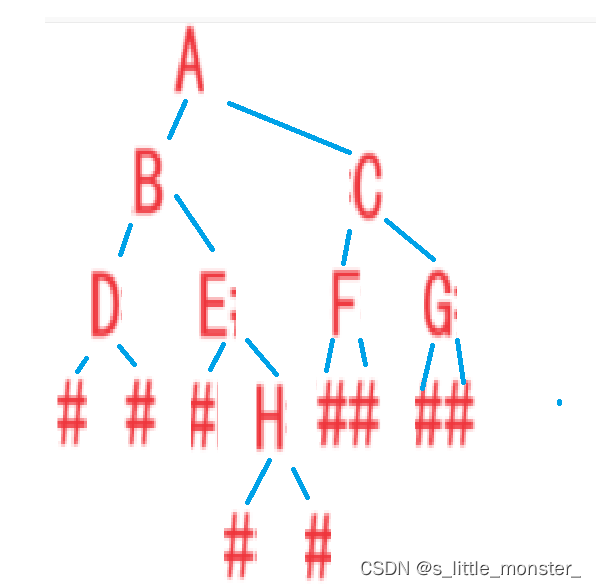
当我们想要求第三层的节点个数时,我们找到BC两棵子树,此时对于BC来说,它们需要找到它第二层的节点个数,再向下递归,此时k==1,将它们不为空的节点返回1
6、二叉树查找
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data = x)return root;BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1)return ret1;//不为空就返回BTNode* ret2 = BinaryTreeFind(root->right, x);if (ret2)return ret2;//不为空就返回return NULL;
}
当节点为空时,返回空
当节点数据为想要查找的数据时,返回该节点指针
递归调用,当左子树中存在这个数时,ret1不为空,返回的就是那个值,右子树同上,都没有就返回空
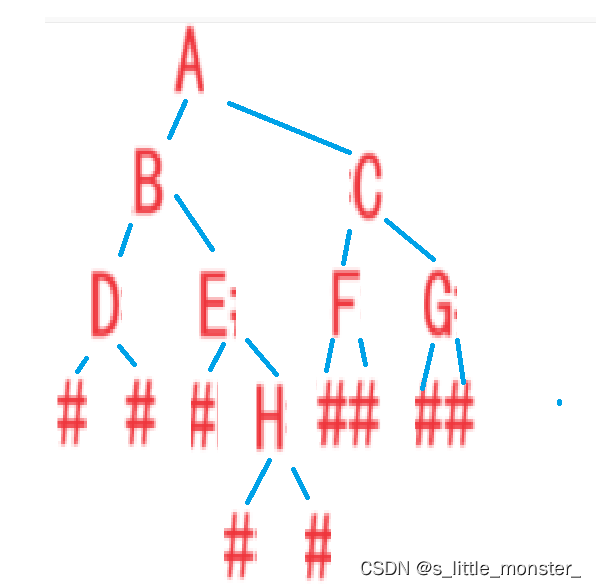
7、前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%c ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}
前序遍历的顺序:根节点->左子树->右子树
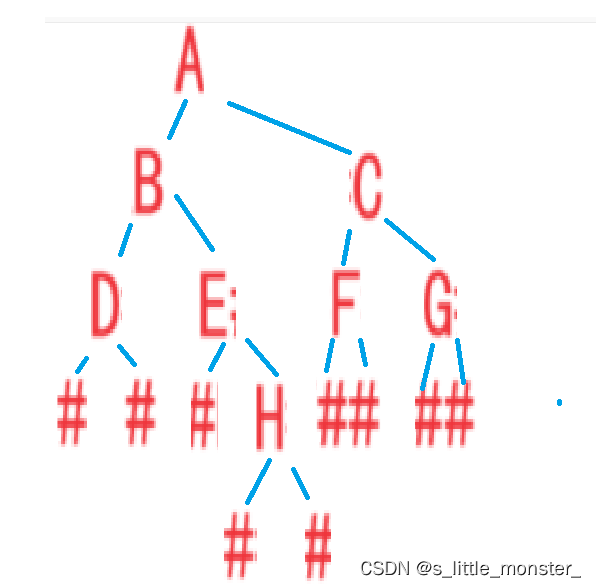
先将根节点A打印之后,递归到左子结点B,打印B,递归到B的左子结点D,打印D,D的左子节点为空,打印N,查看右子节点,也为空,打印N,返回到B,查看右子结点,打印E,以此类推
8、中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BinaryTreeInOrder(root->left);printf("%c ", root->data);BinaryTreeInOrder(root->right);
}
中序遍历顺序:左子树->根->右子树
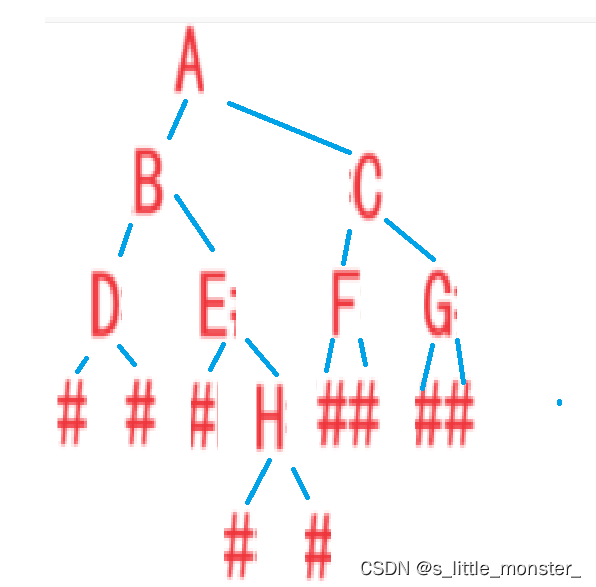
A到B,B到D,D到最底的左子节点,为空,打印N,再打印根D,右子节点,为空,打印N,然后回到B看E,以此类推
9、后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BinaryTreeInOrder(root->left);BinaryTreeInOrder(root->right);printf("%c ", root->data);
}
后序遍历顺序:左子树->右子树->根
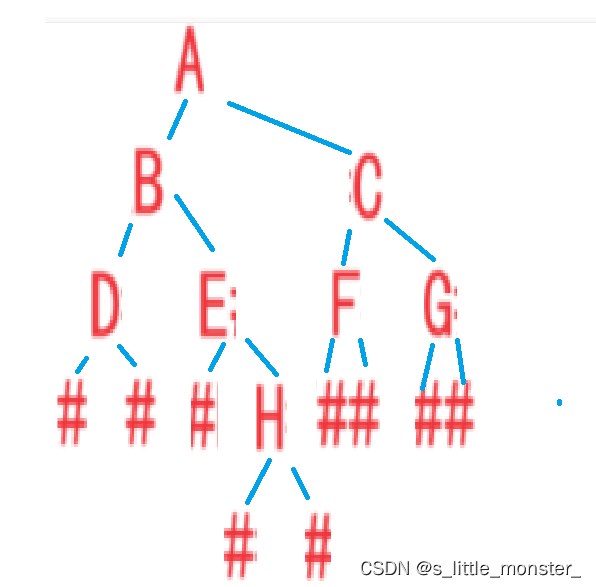
A到B,B到D,D到最底的左子节点,为空,打印N,看D的右子节点,为空,打印N,最后打印D
去到B的右子节点E,以此类推
10、层序遍历与检查二叉树是否为完全二叉树
层序遍历即一层一层的遍历,从第一层开始,此时我们需要一个队列,因为队列可以实现先入先出,并且可以存储数据
Queue.h
#pragma once#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef struct BinaryTreeNode* QDataType;// 链式结构:表示队列
typedef struct QListNode
{struct QListNode* pNext;QDataType data;
}QNode;
// 队列的结构
typedef struct Queue
{QNode* front;QNode* rear;int size;
}Queue;
// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType node);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);
Queue.c
队列我就不添加注释了,前边的文章-栈和队列中都有,可以自行翻阅
#include "Queue.h"void QueueInit(Queue* q)
{assert(q);q->front = q->rear = NULL;q->size = 0;
}void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail\n");return;}newnode->data = x;newnode->pNext = NULL;if (pq->rear == NULL){assert(pq->front == NULL);pq->front = pq->rear = newnode;}else{pq->rear->pNext = newnode;pq->rear = newnode;}pq->size++;
}void QueuePop(Queue* q)
{assert(q);assert(!QueueEmpty(q));if (q->front->pNext == NULL){free(q->front);q->front = q->rear = NULL;}else{QNode* next = q->front->pNext;free(q->front);q->front = next;}q->size--;
}QDataType QueueFront(Queue* q)
{assert(q);assert(!QueueEmpty(q));if (q->front == NULL){return NULL;}return q->front->data;
}int QueueEmpty(Queue* q)
{assert(q);return q->size == 0;
}void QueueDestroy(Queue* q)
{assert(q);QNode* pur = q->front;while (pur){QNode* next = pur->pNext;free(pur);pur = next;}q->front = q->rear = NULL;q->size = 0;
}
层序遍历代码
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);//把根节点作为队列的队头while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);//将要出队的队头数据存储一下QueuePop(&q);//将队头弹出printf("%c ", front->data);//打印被存储的队头数据if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}//从队头开始检查左右子节点,若不为空则添加入队printf("\n");QueueDestroy(&q);
}
完全二叉树判断
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);
//到此的解释如上层序遍历同if (front == NULL)break;
// 遇到空就跳出,只要有空,后面也是空的话,那就是完全二叉树,如果后面不都为空,那么就不是QueuePush(&q, front->left);QueuePush(&q, front->right);//将空之前的数据全部入队}// 检查后面的节点有没有非空while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(&q);return 0;}}QueueDestroy(&q);return 1;
}
今日分享完毕,瑞思拜~

相关文章:

【数据结构】链式二叉树详解
个人主页~ 链式二叉树基本内容~ 链式二叉树详解 1、通过前序遍历的数组来构建二叉树2、二叉树的销毁3、二叉树节点个数4、二叉树叶子节点个数5、二叉树第k层节点个数6、二叉树查找7、前序遍历8、中序遍历9、后序遍历10、层序遍历与检查二叉树是否为完全二叉树Queue.hQueue.c层序…...

PHP面向对象编程总结
PHP面向对象编程总结 学习PHP时,面向对象编程(OOP)往往是一个重要的里程碑。PHP的OOP功能提供了一种更加模块化、可扩展和易于维护的代码结构。在本文中,我们将深入探讨PHP面向对象编程的各个方面,包括类与对象、访问控…...

linux中的“->“符号
问: "->“符号在Linux中是什么意思。 例如:当我在一个特定的文件夹中执行ls -l时,我得到了以下结果。 lrwxrwxrwx 1 root root 11 May 16 13:30 nexus3 -> /nexus-data lrwxrwxrwx 1 root root 29 Feb 27 12:23 ojdbc.jar -&g…...

MySql 数据类型选择与优化
选择优化的数据类型 更小的通常更好 一般情况下尽量使用可以正确存储数据的最小类型。更小的数据类型通常更快,因为它们占用更少的磁盘,内存和CPU缓存,并且处理时需要的CPU周期也更少。但也要确保没有低估需要存储值的范围。 简单就好 简单的…...

HTML静态网页成品作业(HTML+CSS)——家乡常德介绍网页(1个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有1个页面。 二、作品演示 三、代…...

【ARMv7-A】——CP15 协处理器
文章目录 CP15 协处理器指令格式MCR 示例MRC 示例寄存器C0 identification registersC1 system control registersC2 memory protection and control registersC3 memory protection and control registersC4 Not usedC5 Memory system fault registers...

学习笔记:(2)荔枝派Nano开机显示log(全志F1C200S)
学习笔记:TF卡启动荔枝派Nano(全志F1C200S) 1.u-boot配置2.需要配置LCD的显示设备树1.u-boot配置 ARM architecture Enable graphical uboot console on HDMI, LCD or VGAx:480,y:272,depth:...
Qt——升级系列(Level Two):Hello Qt 程序实现、项目文件解析、
Hello Qt 程序实现 使用“按钮”实现 纯代码方式实现: // Widget构造函数的实现 Widget::Widget(QWidget *parent): QWidget(parent) // 使用父类构造函数初始化QWidget,传入父窗口指针, ui(new Ui::Widget) // 创建Ui::Widget类的实例,并…...
)
VUE阻止浏览器记住密码若依CLOUD(INPUT框密码替换圆点)
网上找的要不就是缺少方法要不就是不好用,故发一个完整的 粘贴可用版本 <el-form-item prop"password"><el-input v-model"loginForm.pwdCover" type"text" name"pwd" id"pwd" placeholder"密码" autoco…...

GPT-4o:人工智能新纪元的启航者
引言 随着人工智能技术的不断进步,我们见证了从简单的自动化工具到复杂的决策支持系统的演变。在这一演变过程中,OpenAI的GPT系列无疑占据了领导地位。最近,GPT-4o的推出再次引发了关于AI能力的广泛讨论。本文将对GPT-4o进行详细评价&#x…...

CSRF跨站请求伪造漏洞
CSRF跨站请求伪造漏洞 1.CSRF漏洞概述2.防御CSRF攻击3.CSRF防御绕过CSRF令牌未绑定到用户会话自定义标头令牌绕过绕过Referer检查关键词绕过 4.利用示例使用HTML标签进行GET表单 GET 请求表单POST请求通过 iframe 发送表单 POST 请求Ajax POST 请求 5.CSRF BP 验证方法6.CSRF测…...
)
【Linux】System V 消息队列(不重要)
一、消息队列的原理 一个进程给另一个进程发送类型数据块的方式每一个数据快都被认为是有一个类型的,接收者进程接收的数据快可以有不同的类型值 二、消息队列的接口 和共享内存的接口很像: 消息队列的创建 创建消息队列我们需要用msgget函数&#x…...

label标签
01、label标签 概述 label标签页属于:form元素的成员之一,它有啥意义呢?它主要用来修饰文本和form元素的指向和体验问题。我们只需要把文本和form元素使用label标签包裹,就可以产生一个奇妙的化学反应。就是:我们点击…...

vruntime
vruntime vruntime 变量存放进程的虚拟运行时间,虚拟时间是以 ns 为单位的,which is the actual runtime (the amount of time spent running) normalized (or weighted) by the number of runnable processesvruntime 和定时器节拍不再相关。优先级相同的所有进程的虚拟运行时…...
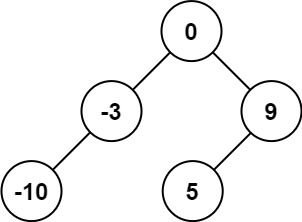
!力扣 108. 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按升序排列,请你将其转换为一棵 平衡二叉搜索树。 示例 1: 输入:nums [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案…...
)
13、matlab使用switch case语句实现两个数字的加减乘除运算以及数据的输入输出(可以设置计算次数)
1、不同数据的键盘输入 函数:input() 代码: a input(请输入一个数字: );%输入数字 c input(请输入一个运算符号: ,s);%输入字符 b input(请输入一个数字: );%输入数字 请输入一个数字: 1 请输入一个运算符号: 请输入一个数字: 2 2、 格式化输出 …...

数学建模 —— 聚类分析(3)
目录 一、聚类分析概述 1.1 常用聚类要素的数据处理 1.1.1 总和标准化 1.1.2 标准差标准化 1.1.3 极大值标准化 1.1.4 极差的标准化 1.2 分类 1.2.1 快速聚类法(K-均值聚类) 1.2.2 系统聚类法(分层聚类法) 二、分类统计…...

java —— 匿名内部类与 Lambda 表达式
一、匿名内部类 匿名内部类是一种没有名称的类,多用于只使用一次的情况,本质上就是其所继承的父类或接口的一个子类。 (一)继承普通类的情况 public class Test{public void method(){System.out.println("通用方法"…...
对红黑树、跳表、B+树的一些理解
文章目录 红黑树应用场景 跳表使用场景 B树使用场景 毫无疑问数据结构是复杂的,让人头大的,大学时唯一挂科的就是数据结构,上学时不用心,不晓得自己的职业生涯要一直被数据结构支配。 或多或少,面试抱佛脚时࿰…...

C++ deque 双端队列
deque原理介绍 deque(双端队列):是一种双开口的"连续"空间的数据结构,双开口的含义是:可以在头尾两端进行插入和删除操作,且时间复杂度为O(1)。 与vector比较,头插效率高,不需要搬移元素…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
