11.7 堆排序
目录
11.7 堆排序
11.7.1 算法流程
11.7.2 算法特性
11.7 堆排序
Tip
阅读本节前,请确保已学完“堆“章节。
堆排序(heap sort)是一种基于堆数据结构实现的高效排序算法。我们可以利用已经学过的“建堆操作”和“元素出堆操作”实现堆排序。
- 输入数组并建立小顶堆,此时最小元素位于堆顶。
- 不断执行出堆操作,依次记录出堆元素,即可得到从小到大排序的序列。
以上方法虽然可行,但需要借助一个额外数组来保存弹出的元素,比较浪费空间。在实际中,我们通常使用一种更加优雅的实现方式。
11.7.1 算法流程
设数组的长度为 𝑛 ,堆排序的流程如图 11-12 所示。
- 输入数组并建立大顶堆。完成后,最大元素位于堆顶。
- 将堆顶元素(第一个元素)与堆底元素(最后一个元素)交换。完成交换后,堆的长度减 1 ,已排序元素数量加 1 。
- 从堆顶元素开始,从顶到底执行堆化操作(sift down)。完成堆化后,堆的性质得到修复。
- 循环执行第
2.步和第3.步。循环 𝑛−1 轮后,即可完成数组排序。
Tip
实际上,元素出堆操作中也包含第 2. 步和第 3. 步,只是多了一个弹出元素的步骤。
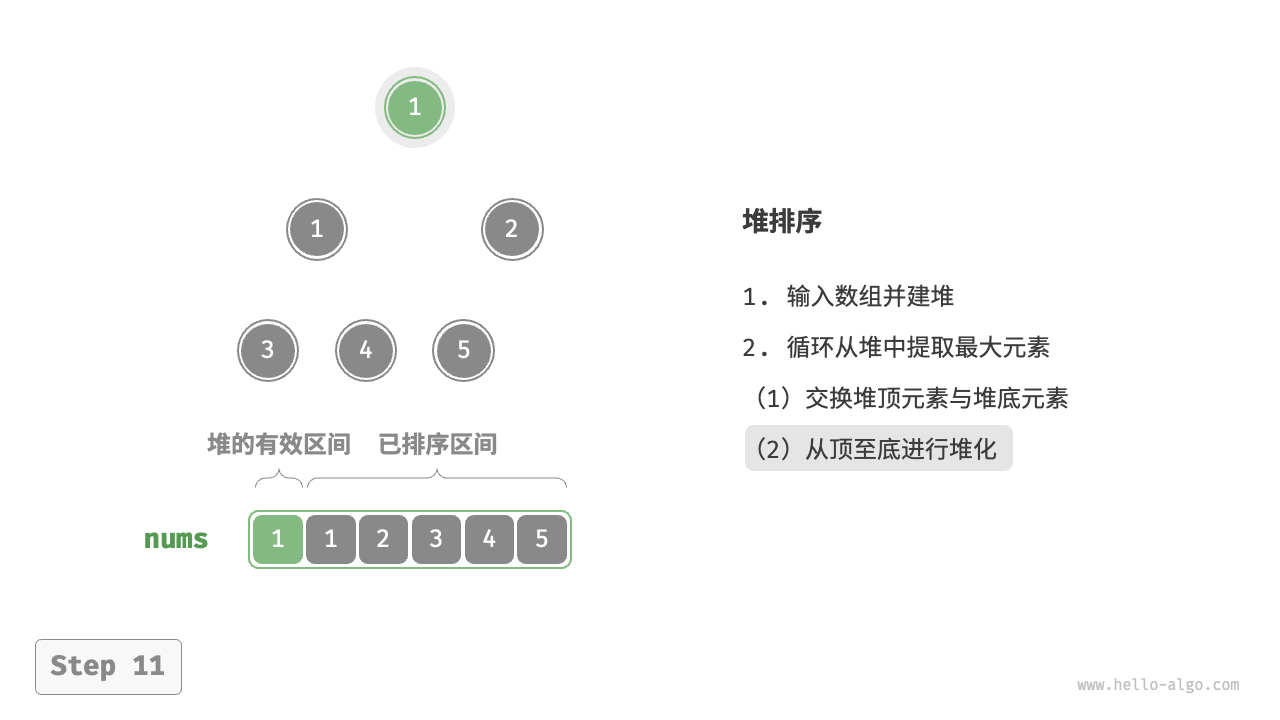
图 11-12 堆排序步骤
在代码实现中,我们使用了与“堆”章节相同的从顶至底堆化 sift_down() 函数。值得注意的是,由于堆的长度会随着提取最大元素而减小,因此我们需要给 sift_down() 函数添加一个长度参数 𝑛 ,用于指定堆的当前有效长度。代码如下所示:
heap_sort.c
/* 堆的长度为 n ,从节点 i 开始,从顶至底堆化 */
void siftDown(int nums[], int n, int i) {while (1) {// 判断节点 i, l, r 中值最大的节点,记为 maint l = 2 * i + 1;int r = 2 * i + 2;int ma = i;if (l < n && nums[l] > nums[ma])ma = l;if (r < n && nums[r] > nums[ma])ma = r;// 若节点 i 最大或索引 l, r 越界,则无须继续堆化,跳出if (ma == i) {break;}// 交换两节点int temp = nums[i];nums[i] = nums[ma];nums[ma] = temp;// 循环向下堆化i = ma;}
}/* 堆排序 */
void heapSort(int nums[], int n) {// 建堆操作:堆化除叶节点以外的其他所有节点for (int i = n / 2 - 1; i >= 0; --i) {siftDown(nums, n, i);}// 从堆中提取最大元素,循环 n-1 轮for (int i = n - 1; i > 0; --i) {// 交换根节点与最右叶节点(交换首元素与尾元素)int tmp = nums[0];nums[0] = nums[i];nums[i] = tmp;// 以根节点为起点,从顶至底进行堆化siftDown(nums, i, 0);}
}
11.7.2 算法特性
- 时间复杂度为 𝑂(𝑛log𝑛)、非自适应排序:建堆操作使用 𝑂(𝑛) 时间。从堆中提取最大元素的时间复杂度为 𝑂(log𝑛) ,共循环 𝑛−1 轮。
- 空间复杂度为 𝑂(1)、原地排序:几个指针变量使用 𝑂(1) 空间。元素交换和堆化操作都是在原数组上进行的。
- 非稳定排序:在交换堆顶元素和堆底元素时,相等元素的相对位置可能发生变化。
相关文章:

11.7 堆排序
目录 11.7 堆排序 11.7.1 算法流程 11.7.2 算法特性 11.7 堆排序 Tip 阅读本节前,请确保已学完“堆“章节。 堆排序(heap sort)是一种基于堆数据结构实现的高效排序算法。我们可以利用已经学过的“建堆操作”和“元素出堆操作”…...

Patchwork++:基于点云的快速、稳健的地面分割方法
1. 背景 论文发表在2022IROS,是Patchwork的改进版本。算法通过数学方法进行快速而鲁棒性很强的地面分割,在智能机器人上的可操作性非常强。通过微调算法,可以应用于16-beams等多种规格的激光雷达。由于激光雷达点云数据标注的难度非常大&…...

Llama改进之——分组查询注意力
引言 今天介绍LLAMA2模型引入的关于注意力的改进——分组查询注意力(Grouped-query attention,GQA)1。 Transformer中的多头注意力在解码阶段来说是一个性能瓶颈。多查询注意力2通过共享单个key和value头,同时不减少query头来提升性能。多查询注意力可能导致质量下…...
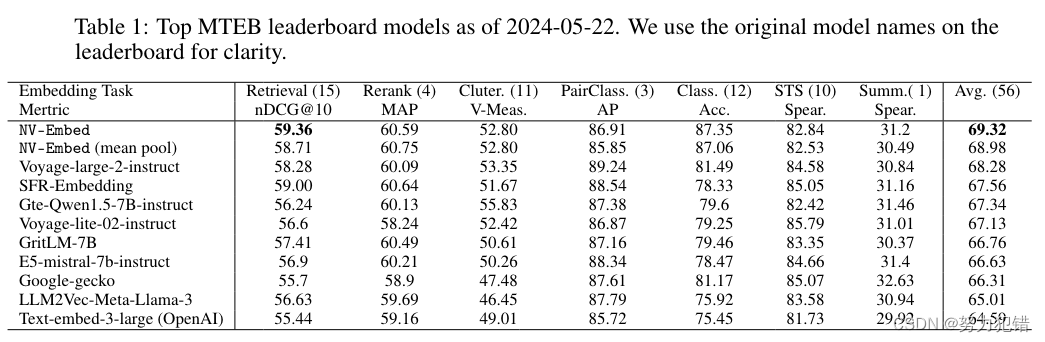
英伟达开源新利器NV-Embed向量模型,基于双向注意力的LLM嵌入模型,MTEB 56项任务排名第一
前言 文本嵌入模型能够将文本信息转化为稠密的向量表示,并在信息检索、语义相似度计算、文本分类等众多自然语言处理任务中发挥着关键作用。近年来,基于解码器的大型语言模型 (LLM) 开始在通用文本嵌入任务中超越传统的 BERT 或 T5 嵌入模型,…...

JVM之【GC-垃圾清除算法】
Java虚拟机(JVM)中的垃圾收集算法主要分为以下几种: 标记-清除算法(Mark-Sweep)复制算法(Copying)标记-整理算法(Mark-Compact)分代收集算法(Generational C…...
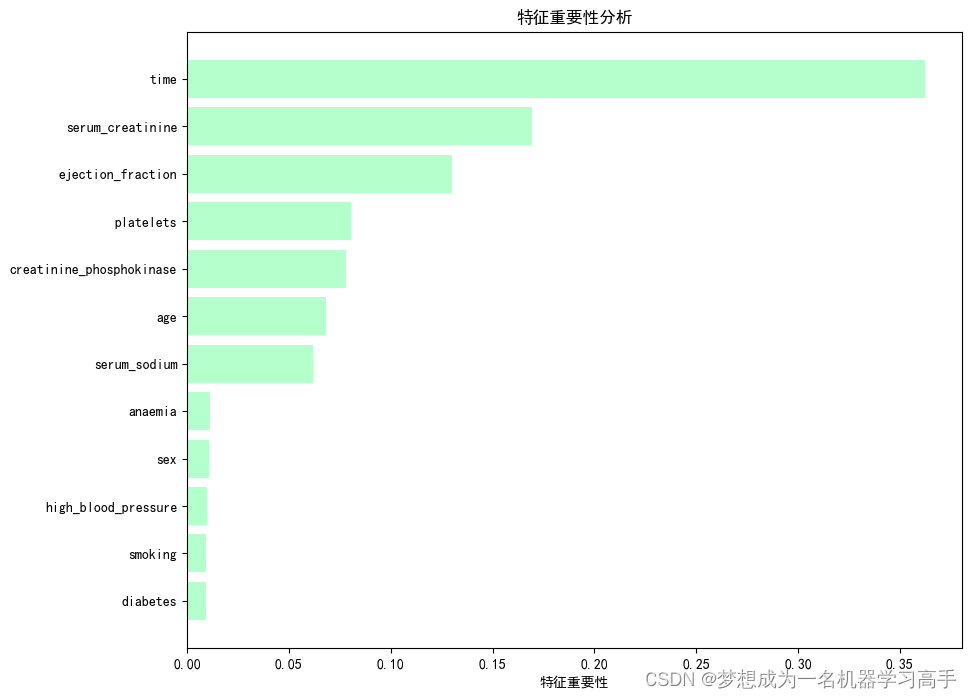
数据分析每周挑战——心衰患者特征数据集
这是一篇关于医学数据的数据分析,但是这个数据集数据不是很多。 背景描述 本数据集包含了多个与心力衰竭相关的特征,用于分析和预测患者心力衰竭发作的风险。数据集涵盖了从40岁到95岁不等年龄的患者群体,提供了广泛的生理和生活方式指标&a…...
)
单例模式(Java实现)
我的相关文章: JavaSE 学习记录-CSDN博客 多线程笔记-CSDN博客 单例模式(Java实现)-CSDN博客 JUC笔记-CSDN博客 注解与反射(Java,类加载机制,双亲委派机制)-CSDN博客 1. 懒汉式线程不安全 pu…...

24.面向对象六大原则
目录介绍 00.面向对象六大原则01.代码单一职责原则02.代码开放封闭原则03.代码里氏替换原则04.代码依赖倒置原则05.代码接口隔离原则06.代码迪米特原则00.面向对象六大原则 六大原则一句话介绍 单一职责原则:指一个类的功能要单一,不能包罗万象。开放封闭原则:指一个模块在扩…...

Vue3-shallowRef与shallowReactive
shallowRef 作用:创建一个响应式数据,但只对顶层属性进行响应式处理。 用法: let myVar shallowRef(initialValue);特点:只跟踪引用值的变化,不关心值内部的属性变化。 shallowReactive 作用:创建一个浅…...

CI/CD(基于ESP-IDF)
主要参考资料 B站乐鑫信息科技《【乐鑫全球开发者大会】DevCon23 #15 |通过 CI/CD 进行流水线开发》 pytest-embedded乐鑫文档: https://docs.espressif.com/projects/pytest-embedded/en/latest/api.html 目录 CI/CD简介乐鑫内部CI/CD测试GitLab CI/CDGitHub Actio…...

聚观早报 | 东风奕派eπ008将上市;苹果Vision Pro发布会
聚观早报每日整理最值得关注的行业重点事件,帮助大家及时了解最新行业动态,每日读报,就读聚观365资讯简报。 整理丨Cutie 6月3日消息 东风奕派eπ008将上市 苹果Vision Pro发布会 特斯拉Model 3高性能版开售 小米14推送全新澎湃OS系统 …...

k8s牛客面经篇
k8s的pod版块: k8s的网络版块: k8s的deployment版块: k8s的service版块: k8s的探针板块: k8s的控制调度板块: k8s的日志监控板块: k8s的流量转发板块: k8s的宏观版块:...

第9周 基于MinIO与OSS实现分布式与云存储
第9周 基于MinIO与OSS实现分布式与云存储 1. 基于mybatis-plus数据修改非空属性忽略更新2. 文件上传3. 分布式文件存储3.1 文件存储架构演变4. Minio docker安装5. 文件服务整合minio依赖minio API测试yml配置minio信息minio配置类业务:上传文件6. 云存储阿里OSS:要钱6.1 依赖6…...

【Linux内核-编程指南】
■ IPC组件 添加链接描述 ■ ■ ■ ■ ■...

Go 编程风格指南 - 最佳实践
Go 编程风格指南 - 最佳实践 原文:https://google.github.io/styleguide/go 概述 | 风格指南 | 风格决策 | 最佳实践 注意: 本文是 Google Go 风格 系列文档的一部分。本文档是 规范性(normative) 但不是强制规范(canonical),并且从属于Goo…...

awk的应用
步骤一:awk的基本用法 1)基本操作方法 格式1:awk [选项] [条件]{指令} 文件 格式2:前置指令 | awk [选项] [条件]{指令} 其中,print 是最常用的编辑指令;若有多条编辑指令,可用分号分隔。 …...
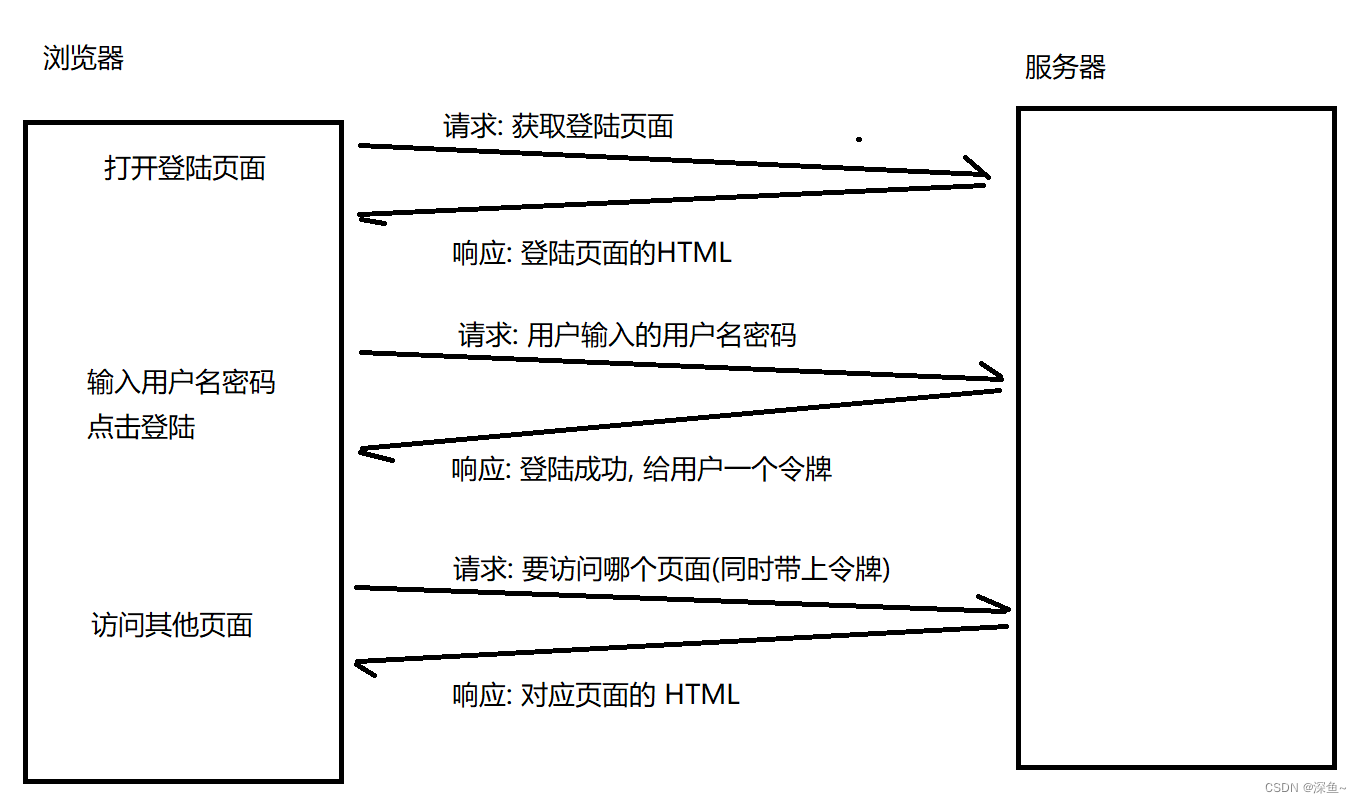
【网络原理】HTTP|认识请求“报头“|Host|Content-Length|Content-Type|UA|Referer|Cookie
目录 认识请求"报头"(header) Host Content-Length Content-Type User-Agent(简称UA) Referer 💡Cookie(最重要的一个header,开发&面试高频问题) 1.Cookie是啥? 2.Cookie怎么存的? …...

深入React Hoooks:从基础到自定义 Hooks
使用 useContext useContext 是另一个常用的 Hook,它可让我们在函数组件中轻松访问 React 的 context。如果你的应用程序依赖于一些全局状态,或者你希望避免将 props 一层一层地传递到子组件,context 很有用。你可以在父组件设置一个值&…...

9.7 Go语言入门(映射 Map)
Go语言入门(映射 Map) 目录六、映射 Map1. 声明和初始化映射1.1 使用 make 函数1.2 使用映射字面量 2. 映射的基本操作2.1 插入和更新元素2.2 访问元素2.3 检查键是否存在2.4 删除元素2.5 获取映射的长度 3. 遍历映射4. 映射的注意事项4.1 映射的零值4.2…...
过期视频怎么恢复?如何从手机、电脑和其他设备中恢复?
过期视频是指那些被误删、丢失或因系统升级等原因而无法正常访问的视频文件。这些视频可能包含了我们珍贵的回忆、重要的信息或者具有商业价值的内容。过期视频的恢复可以帮助我们找回失去的数据,减少损失,提高工作效率和生活质量。过期视频怎么恢复&…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...
