python数据分析——线性模型
参考资料:活用pandas库
1、简单线性回归
线性回归的目标是描述响应变量(或“因变量”)和预测变量(也称“特征”、“协变量”、“自变量”)之间的直线关系。本例中将讨论tips数据集中的total_bill对tip的影响。
# 导入pandas库
import pandas as pd
# 导入数据集
tips=pd.read_csv(r"...\seaborn常用数据案例\tips.csv")
# 展示数据集
print(tips.head())
(1)使用统计模型库
具体相关资料可参考:python统计分析——线性模型的预测和评估_python 线性拟合评估-CSDN博客
# 导入statsmodels库的formula API
import statsmodels.formula.api as smf
# 用普通最小二乘法进行公式拟合
model=smf.ols("tip~total_bill",data=tips)
results=model.fit()
# 用params属性查看线性方程的系数
print(results.params)
# 用conf_int()方法查看置信区间
print(results.conf_int())
# 用summary方法查看整体的结果
print(results.summary())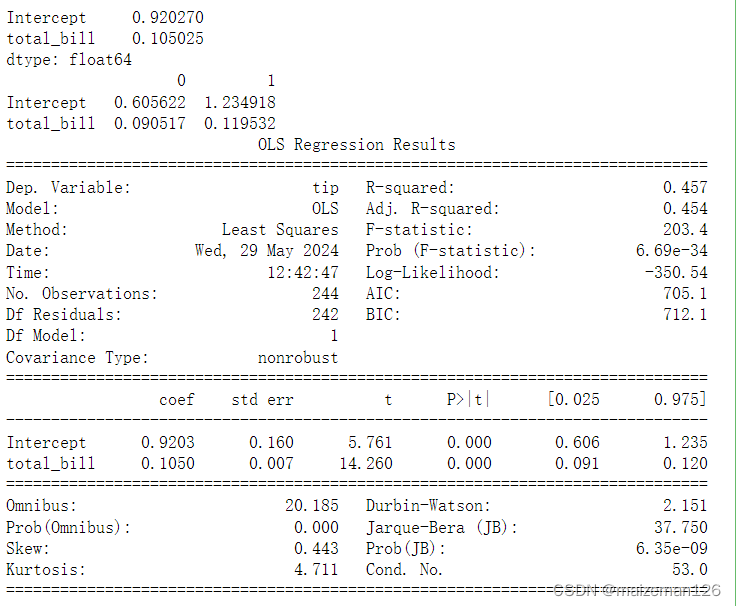
(2)使用sklearn库
由于sklearn接收的是numpy数组,所以有时需要处理数据,以便把DataFrame传入sklearn。如果输入的不是矩阵数据,则需要重塑输入。根据是否只有一个变量或者一个样本,要分别指定reshape(-1,1)或reshape(1,-1)。
# 从sklearn库中导入linear_model模块
from sklearn import linear_model
# 创建LinearRegression()对象
lm=linear_model.LinearRegression()
# 对数据进行拟合
# 注意参数中X是大写,输入的参数是矩阵而非向量
# y是小写,输入的参数是向量
predicted=lm.fit(X=tips['total_bill'].values.reshape(-1,1),y=tips['tip'])
# 输出线性方程的系数
print(predicted.coef_)
# 输出线性方程的截距
print(predicted.intercept_)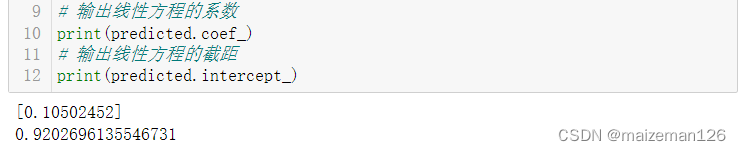
2、多元回归
多元线性回归的系数,是在所有其他变量保持不变的情况下进行解释的。
(1)使用statsmodels库
用多元回归模型拟合数据集与拟合简单的线性回归模型非常相似。在formula参数中,可以轻松地把其他协变量“添加”到波浪线的右边。
# 使用statsmodels库进行多元线性回归的拟合
model=smf.ols("tip~total_bill + size",data=tips).fit()
# 输出结果
print(model.summary())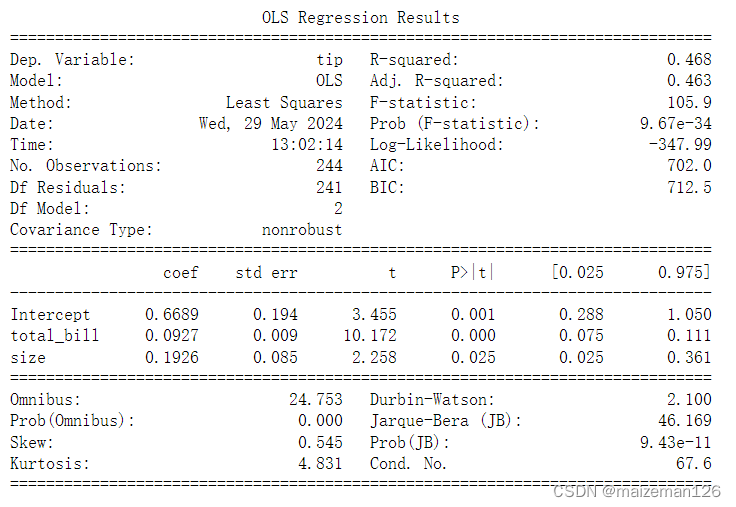
(2)使用statsmodels和分类变量
对分类变量建模时,必须创建虚拟变量,即分类中的每个唯一值都变成了新的二元特征。statsmodels会自动创建虚拟变量。为了避免多重共线性,通常会删除其中一个虚拟变量。
# 拟合所有的变量
model=smf.ols("tip~total_bill + size + sex + smoker + day + time",data=tips).fit()
# 输出结果
print(model.summary())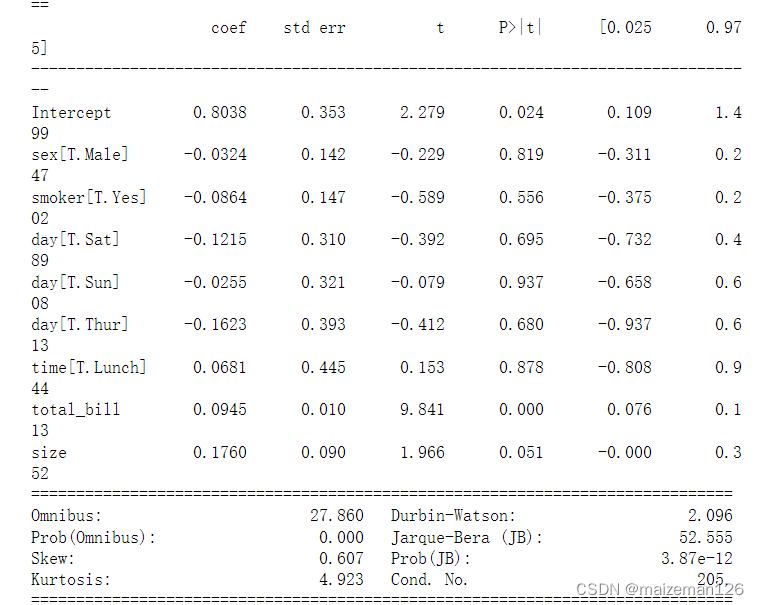
对于分类变量的解释必须和参考变量(即从分析中删除的虚拟变量)联系起来。例如sex[T。Female]的系数为0.0324,解释该值时要与参考值(Male)联系起来。也就是说,当sex从Male变为Female时,tip增加0.0324。
(3)使用sklearn库
在sklearn中,多元回归语法与库中的简单线性回归语法相似,为了想模型添加更多特征,可以把要使用的列传入模型。
# 创建LinearRegression对象
lm=linear_model.LinearRegression()
# 多元线性回归拟合
predicted=lm.fit(X=tips[['total_bill','size']],y=tips['tip'])
# 输出系数和截距
print(predicted.coef_)
print(predicted.intercept_)
(4)使用sklearn和分类变量
必须手动为sklearn创建虚拟变量,可以使用pandas的get_dummies函数来实现。该函数会自动把所有分类变量转换为虚拟变量,所以不必再逐个传入各列。sklearn中OneHotEncoder函数与之类似。
# 用get_dummies函数创建虚拟变量
tips_dummy=pd.get_dummies(tips[['total_bill','size','sex','smoker','day','time']])
# 展示tips_dummy
print(tips_dummy.head())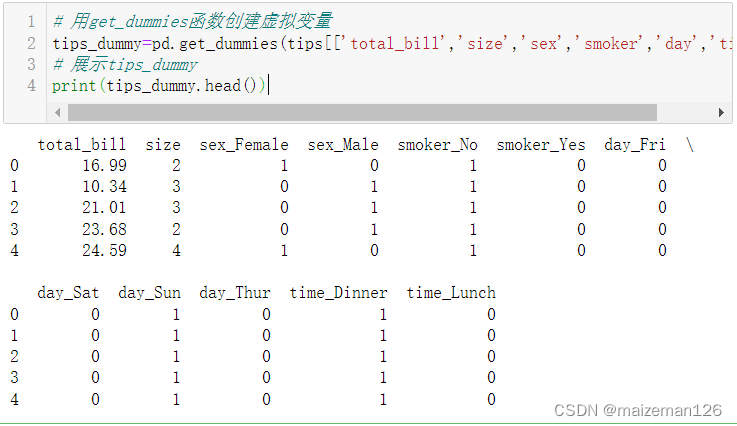
可以向get_dummies函数传入drop_first=True来删除参考变量。
x_tips_dummy_ref=pd.get_dummies(tips[['total_bill','size','sex','smoker','day','time']],drop_first=True)
print(x_tips_dummy_ref.head())
lm=linear_model.LinearRegression()
predicted=lm.fit(X=x_tips_dummy_ref,y=tips['tip'])
print(predicted.coef_)
print(predicted.intercept_)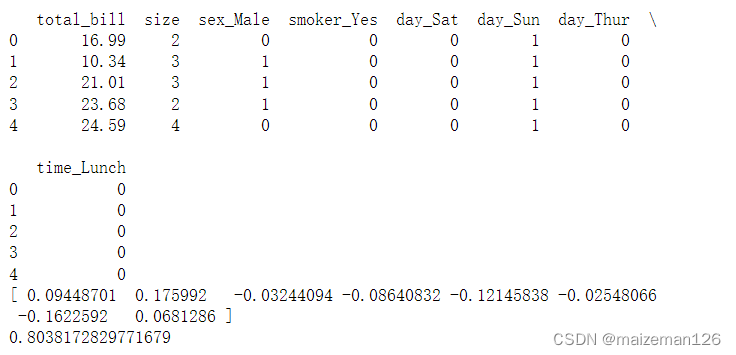
3、保留sklearn的索引标签
在尝试解释sklearn模型时,一个棘手的问题就是模型的系数不带标签,原因是numpy ndarray无法存储这类元数据。如果想让输出结果和statsmodels类似,需要手动存储标签,并添加系数。
# 导入numpy库
import numpy as np
# 创建模型并拟合
lm=linear_model.LinearRegression()
predicted=lm.fit(X=x_tips_dummy_ref,y=tips['tip'])
# 获取截距以及其他系数
values=np.append(predicted.intercept_,predicted.coef_)
# 获取值得名称
names=np.append('intercept',x_tips_dummy_ref.columns)
# 把所有所项目放入一个带标签的DataFrame中
results=pd.DataFrame(values,index=names,columns=['coef'])
print(results)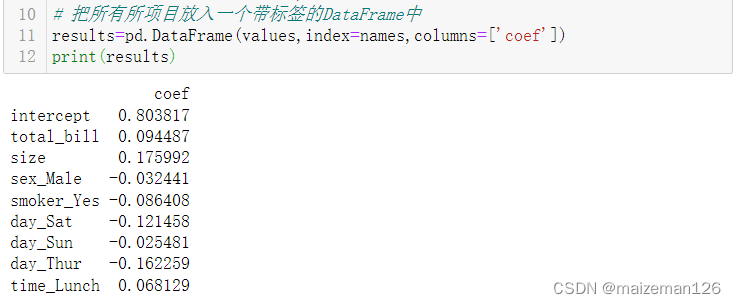
相关文章:

python数据分析——线性模型
参考资料:活用pandas库 1、简单线性回归 线性回归的目标是描述响应变量(或“因变量”)和预测变量(也称“特征”、“协变量”、“自变量”)之间的直线关系。本例中将讨论tips数据集中的total_bill对tip的影响。 # 导入…...

网络原理——HTTP/HTTPS ---- HTTPS
T04BF 👋专栏: 算法|JAVA|MySQL|C语言 🫵 今天你敲代码了吗 目录 HTTPS加密与解密HTTPS的工作流程使用对称密钥来加密使用非对称密钥 来对 对称密钥进行加密第三方公证总结 HTTPS https本质上就是在http的基础之上 增加了加密层,抛开加密层之后,剩下的部…...
网络协议二
一、套接字Socket 基于 TCP UDP 协议的 Socket 编程,在讲 TCP 和 UDP 协议的时候,我们分客户端和服务端,在写程序的时候,我们也同样这样分。 在网络层,Socket 函数需要指定到底是 IPv4 还是 IPv6,分别对应设…...

内存映射mmap技术详解
一、mmap基础概念 mmap 即 memory map,也就是内存映射。mmap 是一种内存映射文件的方法,即将一个文件或者其它对象映射到进程的地址空间,实现文件磁盘地址和进程虚拟地址空间中一段虚拟地址的一一对映关系。实现这样的映射关系后,…...

react 合成事件
React合成事件-CSDN博客 当然,很高兴为你解释React中的合成事件概念,非常适合React初学者理解。 想象一下,你正在组织一场派对,为了让派对顺利进行,你需要管理各种活动,比如游戏、音乐和食物分配。但是&a…...
springboot配置集成RedisTemplate和Redisson,使用分布式锁案例
文章要点 自定义配置属性类集成配置RedisTemplate集成配置分布式锁Redisson使用分布式锁简单实现超卖方案 1. 项目结构 2. 集成RedisTemplate和Redisson 添加依赖 依赖的版本与继承的spring-boot-starter-parent工程相对应,可写可不写 <!--spring data redis…...

随机数相关
产生随机数对象 固定写法: Random 随机数变量名 new Random();Random r new Random();生成随机数 int i r.Next(); //生成一个非负数的随机数 Console.WriteLine(i);i r.Next(100); // 生成一个 0~99的随机数 左边始终是0 左包含 右边是100 右不包含 Consol…...
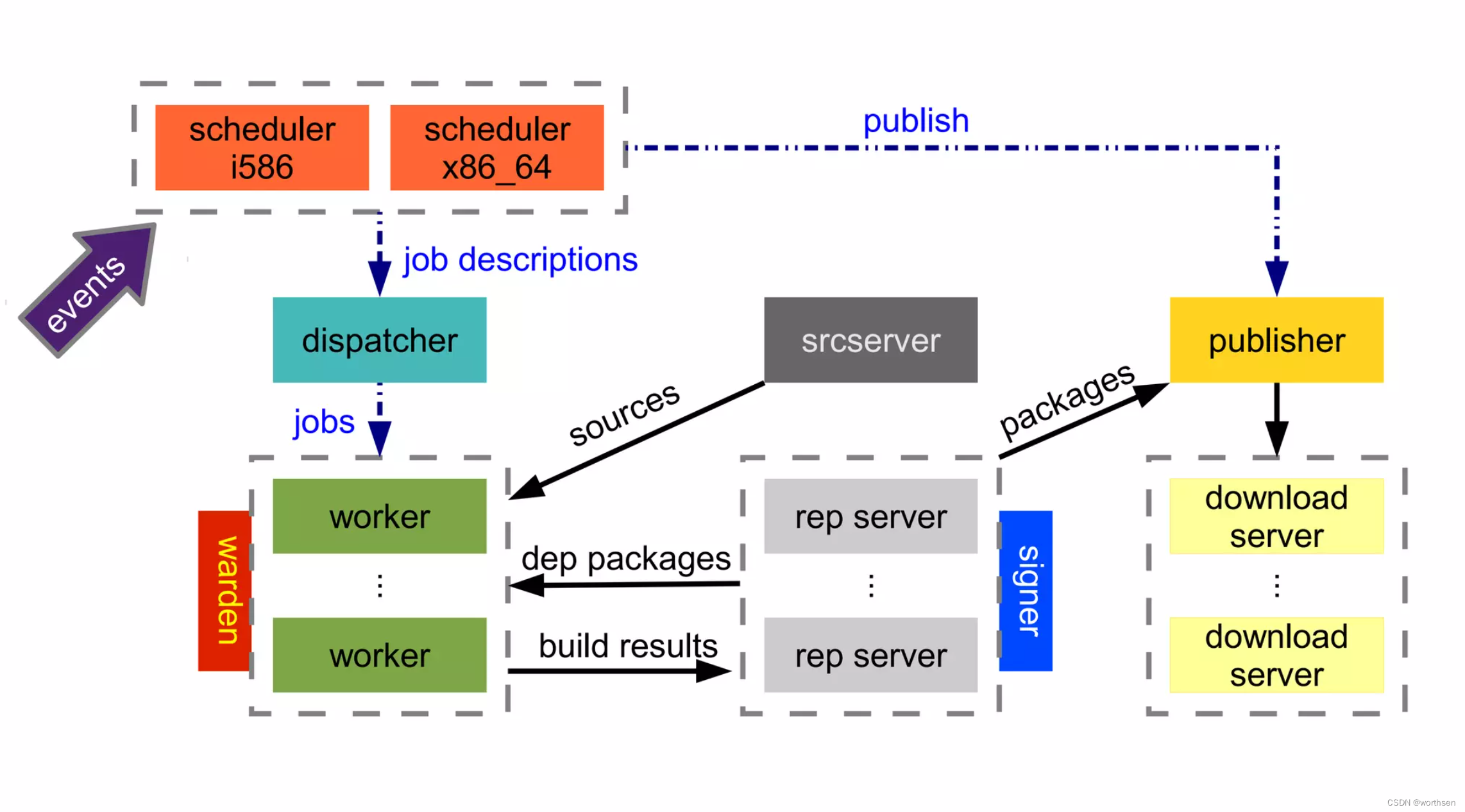
EulerMaker Yocto Open Build Service
EulerMaker & Yocto & Open Build Service 1 介绍1.1 概述 2 工具2.1 Yocto 【嵌入式领域】介绍目标好处三大关键组件创建流程发行版本 2.2 Open Build Service 【OBS】【服务器领域】介绍应用 2.3 EulerMaker 【全场景】介绍特性需求背景(1)能支…...
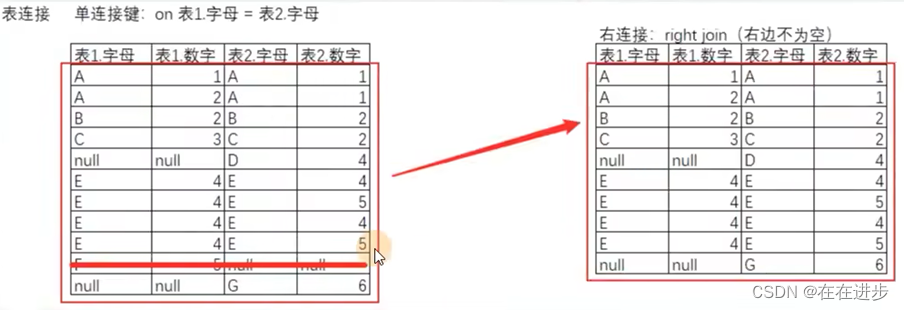
SQL面试问题集
目录 Q.左连接和右连接的区别 Q.union 和 union all的区别 1、取结果的交集 2、获取结果后的操作 Q.熟悉开窗函数吗?讲一下row_number和dense_rank的区别。 Q.hive行转列怎么操作的 Q.要求手写的题主要考了聚合函数和窗口函数,row_number()&#…...

基于单片机的八路抢答器设计论文
绪 论1.1 课题研究的相关背景 抢答器是一种应用非常广泛的设备,在各种竞赛、抢答场合中,它能迅速、客观地分辨出最先获得发言权的选手。早期的抢答器只由几个三极管、可控硅、发光管等组成,能通过发光管的指示辩认出选手号码。现在大多数抢答器均使用单片机(如MCS-5…...

一个最简单基于spring的websocket服务端+客户端实现案例
1、服务端 代码分为两部分: 一个是服务器终端类:用java注解来监听连接ServerEndpoint、连接成功OnOpen、连接失败OnClose、收到消息等状态OnMessage import org.springframework.stereotype.Component;import javax.websocket.*; import javax.websoc…...

三.二、关于 Vue.js 中`transition`组件使用:页面切换动画和标签移动动画都是要用到的
一、引言 在 Vue.js 中,transition组件提供了一种简单而强大的方式来实现页面过渡效果。它可以让元素在状态改变时,如进入或离开视图时,以平滑的动画方式进行过渡。通过transition,我们可以为应用增添更加生动和吸引人的用户体验…...

指纹考勤系统
目录 1.课题研究目的和内容 1.1 课题研究目的 1.2 课题研究内容 2.系统总体方案设计及功能模块介绍 2.1总体方案设计 2.2 ATK-301模块介绍 2.3 TFTLCD显示功能模块介绍 2.4 蜂鸣器报警功能模块介绍 2.5 时钟模块介绍 3.系统硬件设计与实现 3.1 系统硬件电…...
怎么找抖音视频素材?下载抖音的素材视频网站分享给你
在这个视觉印象至关重要的时代,选用高质量的视频素材对于制作抖音视频来说是关键。如果你正在寻找适合的视频素材来丰富你的抖音创作,以下这份详细的视频素材网站指南将帮助你迈出第一步。 蛙学府网 蛙学府网提供了丰富多样的视频素材,包括动…...
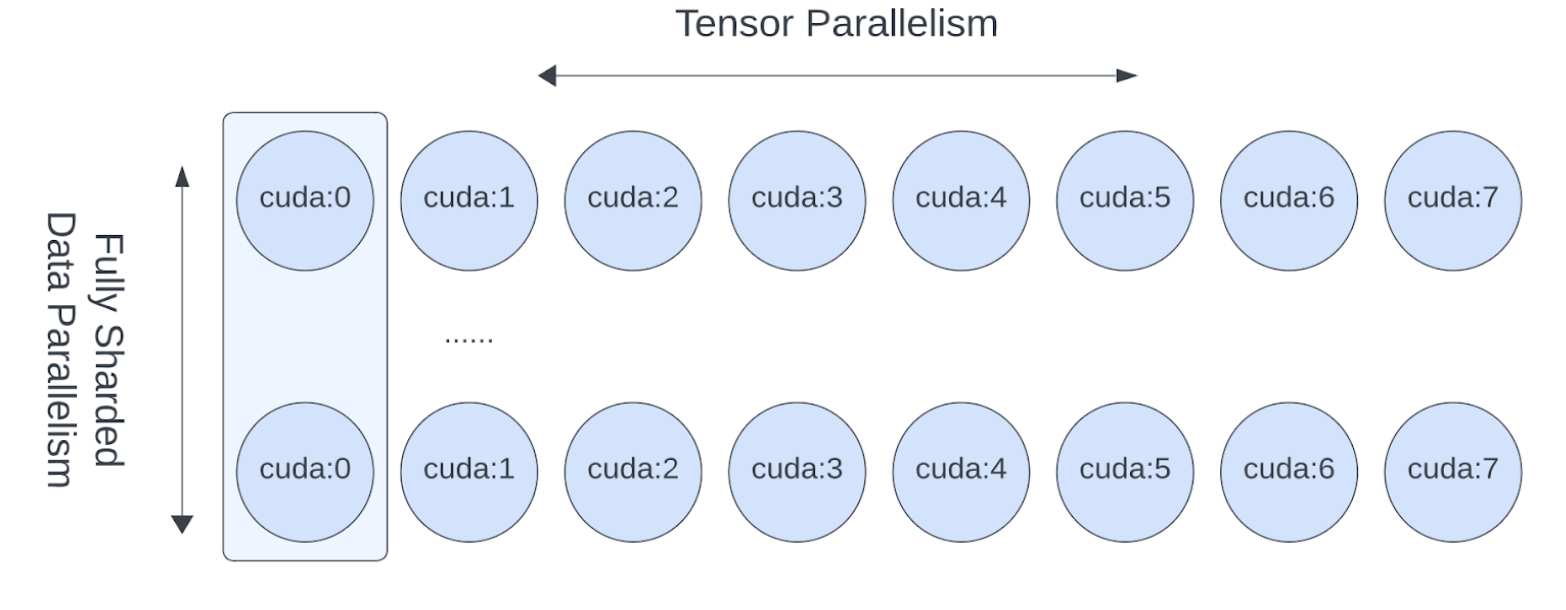
【pytorch】大模型训练张量并行
Large Scale Transformer model training with Tensor Parallel (TP) 张量并行如何工作 原始 Tensor Parallel (TP) 模型并行技术于Megatron-LM论文中被提出,是一种用于培育大规模Transformer模型的高效模型并行技术。我们在本练习指南中介绍的序列并行 (SP) 实际…...

Flutter 中的 CupertinoSliverNavigationBar 小部件:全面指南
Flutter 中的 CupertinoSliverNavigationBar 小部件:全面指南 Flutter 是一个由 Google 开发的跨平台 UI 框架,它允许开发者使用 Dart 语言来构建高性能、美观的移动、Web 和桌面应用。在 Flutter 的丰富组件库中,CupertinoSliverNavigation…...

【数据库系统概论】程序题
“学生管理数据库”包含以下三个表,即学生表Student、课程表Course和选课表SC,结构如下: Student(Sno,Sname,Ssex,Sage,Sdept)Course (Cno,Cname&…...
群体优化算法---蝙蝠优化算法分类Iris数据集
介绍 蝙蝠算法(Bat Algorithm, BA)是一种基于蝙蝠回声定位行为的优化算法。要将蝙蝠算法应用于分类问题,可以通过将蝙蝠算法用于优化分类器的参数,图像分割等 本文示例 我们使用一个经典的分类数据集,如Iris数据集&…...

【C++】类和对象1.0
本鼠浅浅介绍一些C类和对象的知识,希望能得到读者老爷们的垂阅! 目录 1.面向过程和面向对象 2.类的引入 3.类的定义 4.类的访问限定符及封装 4.1.类的访问限定符 4.2.封装 5.C中struct和class的区别 6.类域 7.类的实例化 8.类对象模型 8.1.类…...

Linux下gcc编译32位程序报错
gcc使用-m32选项,编译32位程序时,报错:/usr/include/stdio.h:27:10: fatal error: bits/libc-header-start.h: No such file or directory gcc编译32位程序时,报错:/usr/include/stdio.h:27:10: fatal error: bits/li…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
