当前位置： 首页 > news >正文

上传RKP 证书签名请求息上传到 Google 的后端服务器

news 2026/2/11 2:39:52

上传证书签名请求

1.准备环境：OK

pip3 install google-auth==2.13.0 requests==2.28

在这里插入图片描述
下载 device_info_uploader.py 。
在这里插入图片描述
没找到先跳过

选项 1：通过 GCP 帐户使用 device_info_uploader.py

  1. 运行脚本。
./device_info_uploader.py --credentials /secure/storage/cred.json --json-csr
csrs.json --cache-token --company-id COMPANY_ID
  1. 等待脚本输出，其中包含要登录的 URL。
  2. 复制脚本输出中显示的登录 URL 并将其粘贴到新的浏览器选项卡中（这将打开 Google 登录屏
    幕）。选择您的公司帐户（格式为 android-partner-api@company.com ）。
  3. 选择“允许”以授予对您帐户的测试访问权限，使其能够查看和管理合作伙伴设备信息。

相关文章：

上传RKP 证书签名请求息上传到 Google 的后端服务器

上传证书签名请求 1.准备环境：OK pip3 install google-auth2.13.0 requests2.28下载 device_info_uploader.py 。 没找到先跳过 选项 1：通过 GCP 帐户使用 device_info_uploader.py 运行脚本。 ./device_info_uploader.py --credentials /secure/s…...

编程日记 2024/6/4 18:29:43

Debian和ubuntu 嵌入式的系统的 区别

随着开源操作系统的日益流行，Debian和Ubuntu这两个基于Linux的发行版本成为了众多开发者和系统管理员的首选。它们各自拥有独特的优势和特点，那么，在选择时，哪一个更适合你呢？接下来，我们将深入探讨两者的关…...

编程日记 2024/6/4 18:26:39

HTML旋转照片盒子

效果图 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><meta http-equiv"X-UA-Compatible" content…...

编程日记 2024/6/4 18:25:38

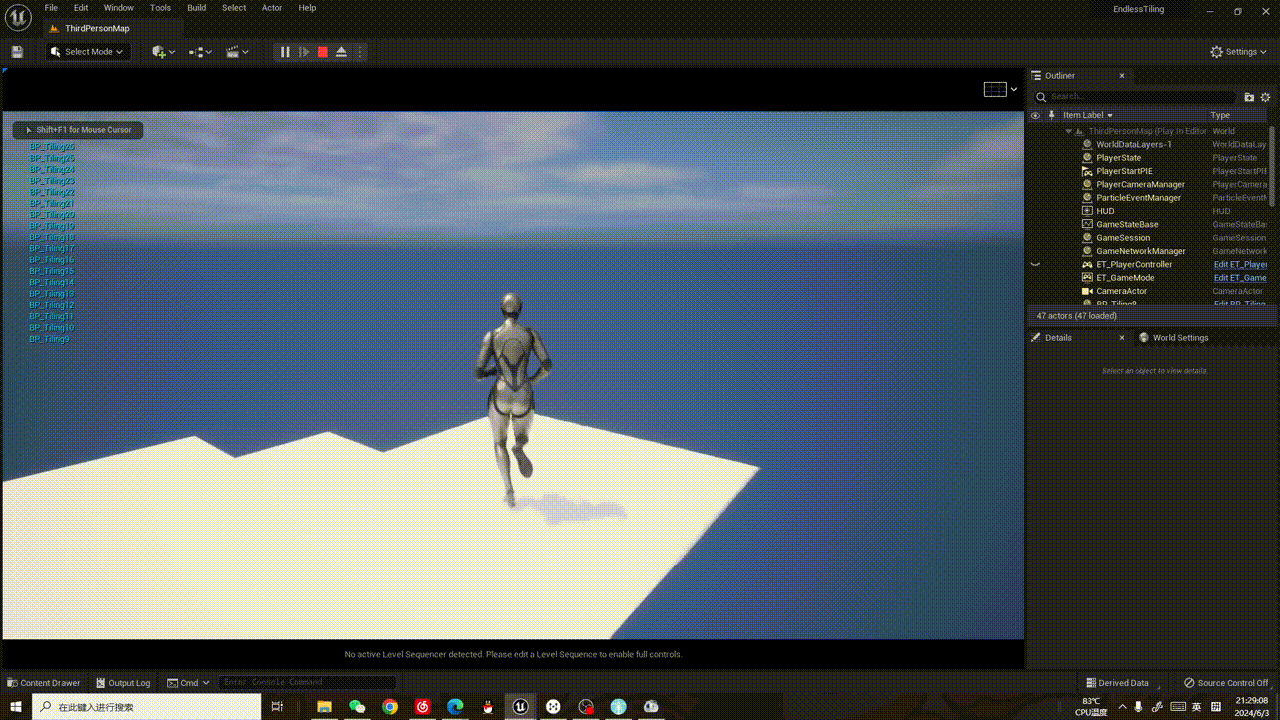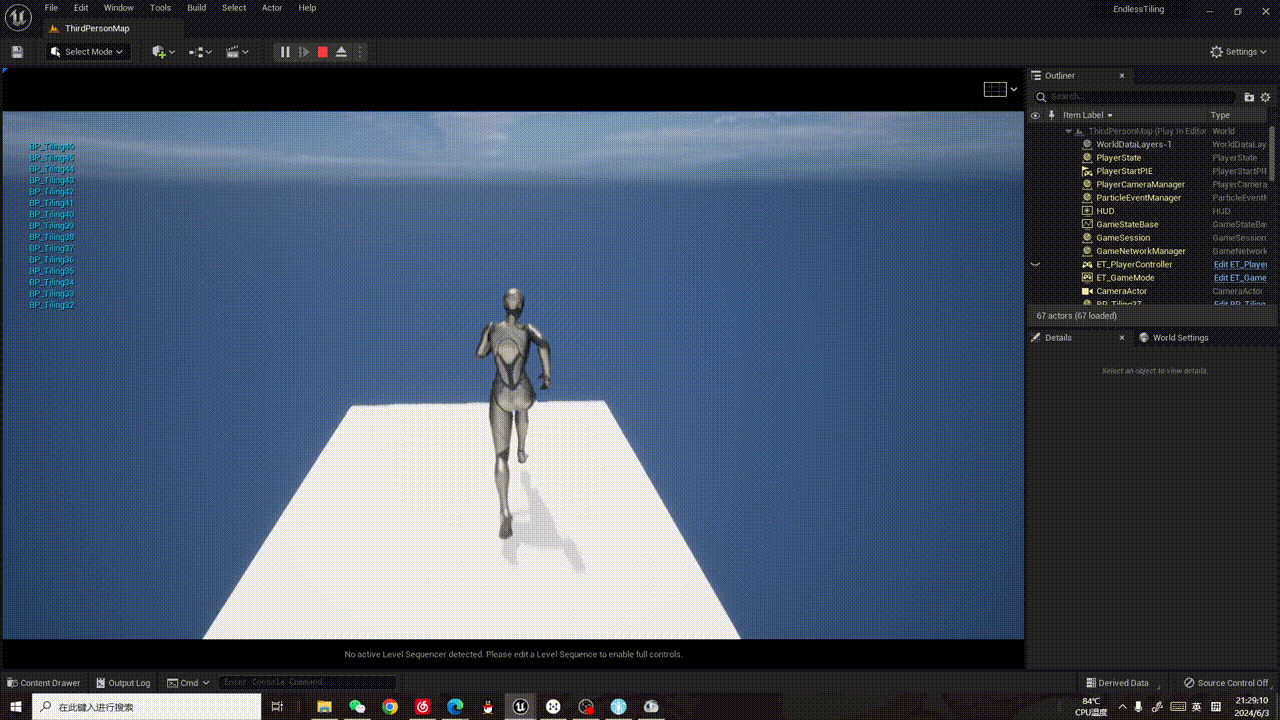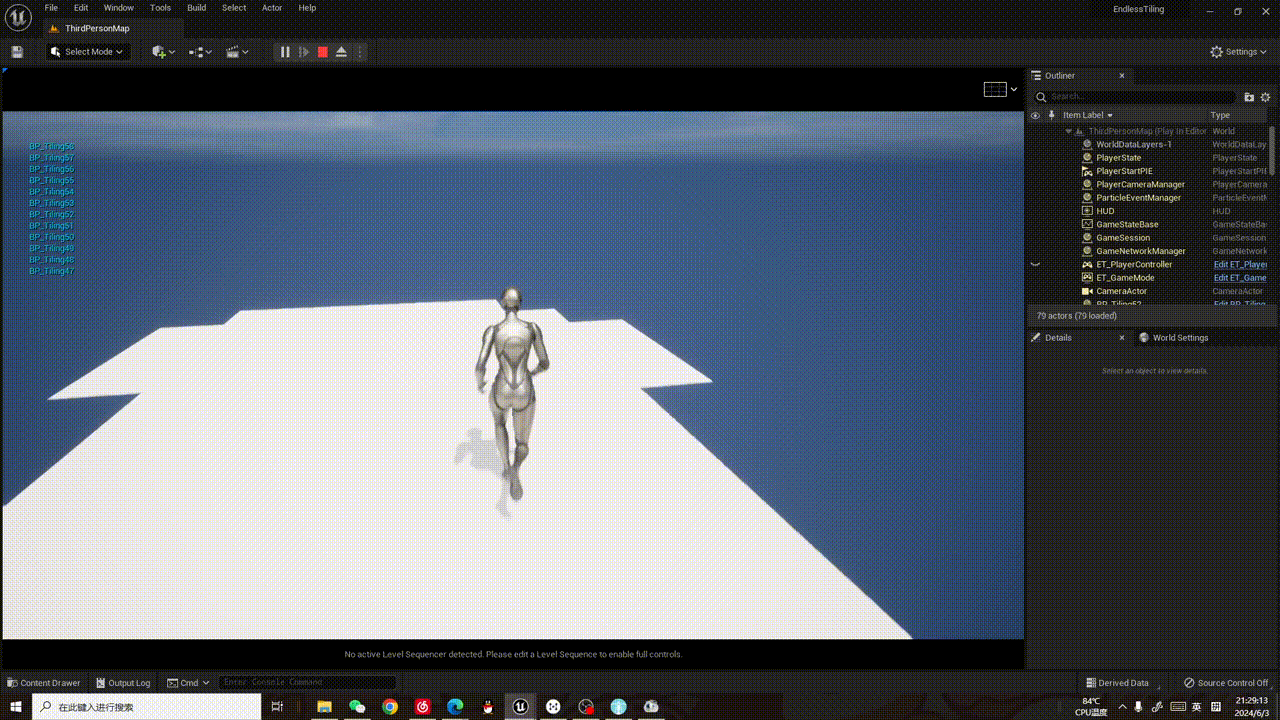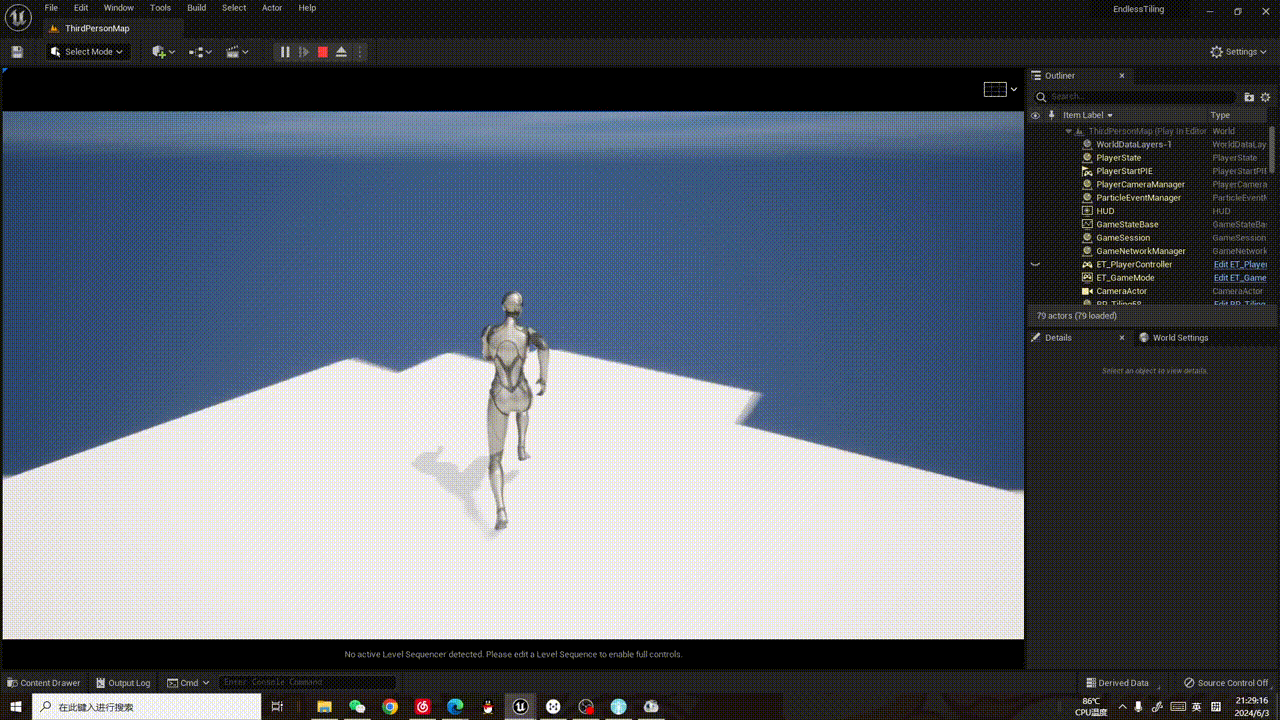
【UE5 刺客信条动态地面复刻】实现无界地面01：动态生成

2024.6.4更新 昨天半夜意识到生成Cube的方案不合适&#xff0c;又开始到处找动态地面的方法&#xff0c;发现了我想要的效果直接可以用nigara实现&#xff01;&#xff01;&#xff01;&#xff01; 于是这个部分就暂时告一段落&#xff0c;今季开始新的方向的学习。 为了快速…...

编程日记 2024/6/4 18:24:37

AI产品经理系列-如何使用kimi快速撰写用户故事(含提示词)

在AI时代&#xff0c;可能人人都可成为产品经理。 之前我们聊过如何使用kimi协助完成产品需求文档&#xff0c;如何写竞品分析报告&#xff0c;这一篇我们聊聊用户故事&#xff0c;如何使用kimi协助撰写产品需求文档中的用户故事。 在此之前我们先了解下什么是用户故事&#…...

编程日记 2024/6/4 18:23:36

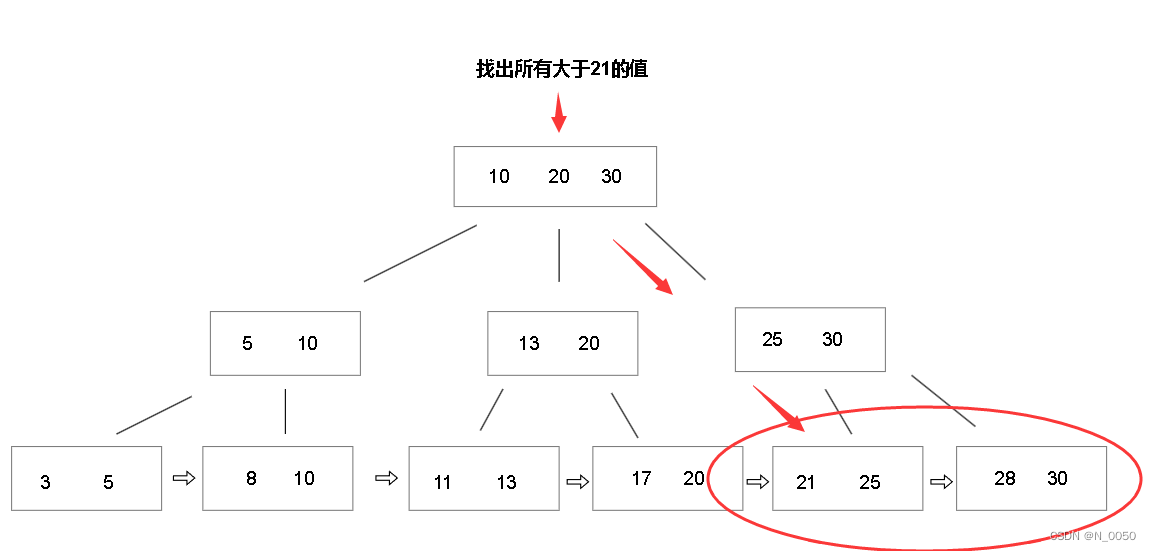
MySQL索引与事务

前言&#x1f440;~ 紧接着数据库的相关知识&#xff0c;今天讲解MySQL面试中频繁被问到的知识点&#xff0c;索引与事务!!! 如果各位对文章的内容感兴趣的话&#xff0c;请点点小赞&#xff0c;关注一手不迷路&#xff0c;如果内容有什么问题的话&#xff0c;欢迎各位评论纠正…...

编程日记 2024/6/4 18:21:29

『大模型笔记』从基础原理出发提升深度学习性能

从基础原理出发提升深度学习性能 文章目录 一. 从基础原理出发提升深度学习性能1.1. 计算（compute）1.2. 带宽（Bandwidth）1.2.1 关于内存带宽成本的推理(Reasoning about Memory-Bandwidth Costs)1.3. 开销（Overhead）二. 总结三. 参考文献Making Deep Learning Go Brrrr F…...

编程日记 2024/6/4 18:19:27

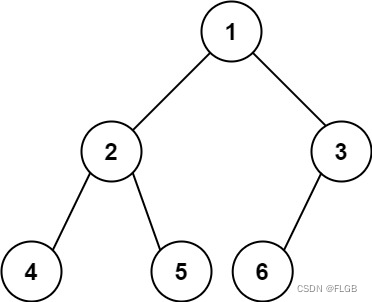
【二叉树】Leetcode 222. 完全二叉树的节点个数【简单】

完全二叉树的节点个数 你一棵 完全二叉树 的根节点 root &#xff0c;求出该树的节点个数。 完全二叉树 的定义如下&#xff1a;在完全二叉树中&#xff0c;除了最底层节点可能没填满外&#xff0c;其余每层节点数都达到最大值&#xff0c;并且最下面一层的节点都集中在该层最…...

编程日记 2024/6/4 18:18:26

golang界面设计器，全网少见

今天登录govcl的网站&#xff0c;无意中看到有个简易UI设计器。 对于golang的UI专用设计器&#xff0c;还没在网上真正见过。 之前也用govcl来做过两三个桌面应用&#xff0c;好用是好用&#xff0c;不过要安装Lazarus的IDE来拖动设计UI&#xff0c;还要配置很多东西&#xff0…...

编程日记 2024/6/4 18:17:25

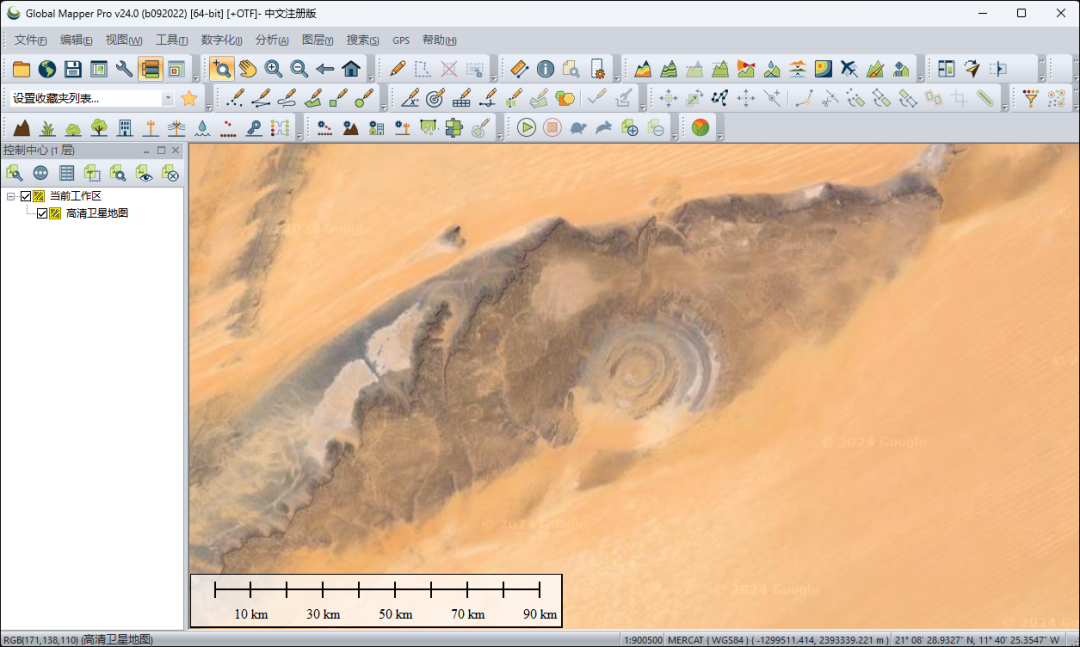
如何在GlobalMapper中加载高清卫星影像？

GlobalMapper在GIS行业几乎无人不知&#xff0c;无人不晓&#xff0c;但它可以直接加载卫星影像也许就不是每个人都知道的了。 这里就来分享一下如何在GlobalMapper中加载高清卫星影像&#xff0c;并可以在文末查看领取软件安装包和图源的方法。 如何加载高清图源 首先&…...

编程日记 2024/6/4 18:16:23

【机器学习】解锁AI密码：神经网络算法详解与前沿探索

&#x1f440;传送门&#x1f440; &#x1f50d;引言&#x1f340;神经网络的基本原理&#x1f680;神经网络的结构&#x1f4d5;神经网络的训练过程&#x1f686;神经网络的应用实例&#x1f496;未来发展趋势&#x1f496;结语 &#x1f50d;引言 随着人工智能技术的飞速发…...

编程日记 2024/6/4 18:15:23

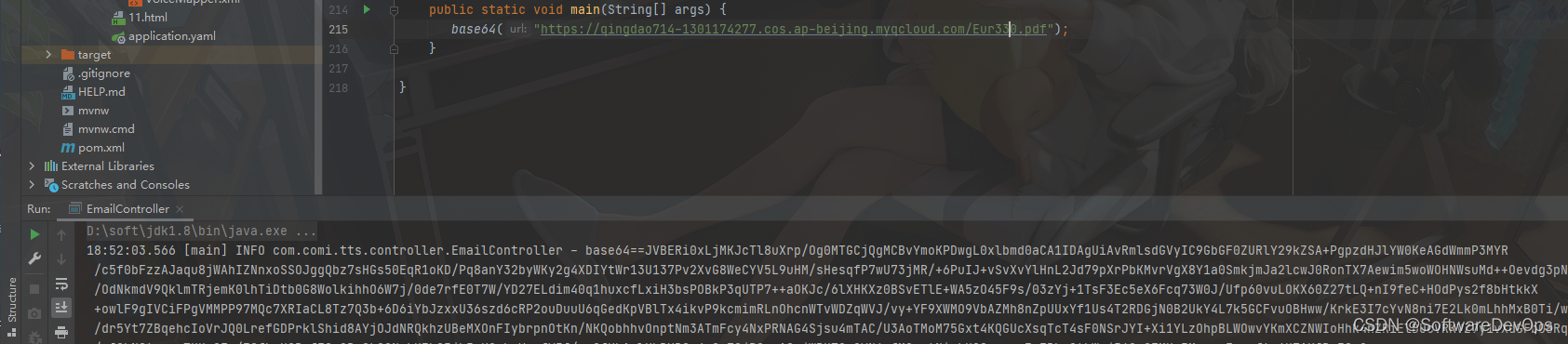
Java如何实现pdf转base64以及怎么反转？

问题需求 今天在做发送邮件功能的时候&#xff0c;发现邮件的附件部分&#xff0c;比如pdf文档&#xff0c;要求先把pdf转为base64&#xff0c;邮件才会发送。那接下来就先看看Java 如何把 pdf文档转为base64。 两种方式&#xff0c;一种是通过插件 jar 包的方式引入&#xf…...

编程日记 2024/6/4 18:08:16

动态规划5：62. 不同路径

动态规划解题步骤&#xff1a; 1.确定状态表示&#xff1a;dp[i]是什么 2.确定状态转移方程&#xff1a;dp[i]等于什么 3.初始化&#xff1a;确保状态转移方程不越界 4.确定填表顺序&#xff1a;根据状态转移方程即可确定填表顺序 5.确定返回值 题目链接&#xff1a;62. …...

编程日记 2024/6/4 18:07:13

Python编程学习第一篇——Python零基础快速入门（五）-列表（List）

今天我们来一起学习Python的列表&#xff08;list&#xff09;&#xff0c;Python中的列表&#xff08;List&#xff09;是一种有序、可变的数据结构&#xff0c;可以用来存储多个值。列表可以包含不同类型的数据&#xff0c;例如整数、浮点数、字符串等。以下是关于Python列表…...

编程日记 2024/6/4 18:06:12

c# - 运算符 ＜＜ 不能应用于 long 和 long 类型的操作数

Compiler Error CS0019 c# - 运算符 << 不能应用于 long 和 long 类型的操作数 处理方法 特此记录 anlog 2024年5月30日...

编程日记 2024/6/4 18:03:09

问题排查｜记录一次基于mymuduo库开发的服务器错误排查(回响服务器无法正常工作)

问题背景&#xff1a; 服务器程序如下&#xff1a; #include <mymuduo/TcpServer.h> #include <mymuduo/Logger.h>#include <string> #include <functional>class EchoServer { public:EchoServer(EventLoop *loop,const InetAddress &addr, con…...

编程日记 2024/6/4 18:01:06

中介模式实现聊天室

中介者模式的核心逻辑就是解耦对象‘多对多’的相互依赖关系。当遇到一大堆混乱的对象呈现“网状结构”&#xff0c;利用通过中介者模式解耦对象之间的通讯。 代码案例 抽象中介类 public abstract class AbstractChatRoom {public abstract void notice(String message , Us…...

编程日记 2024/6/4 18:00:05

游戏开发与游戏设计区别

游戏设计与游戏开发是两个紧密相关但有着不同重点的领域&#xff0c;通常需要不同的技能和流程。以下是对游戏设计与游戏开发的详细解释&#xff0c;以及两者的区别&#xff1a; 游戏设计是关于构思和规划游戏的内容、机制和体验的过程。 主要内容: 故事和情节&#xff1a;构…...

编程日记 2024/6/4 17:59:04

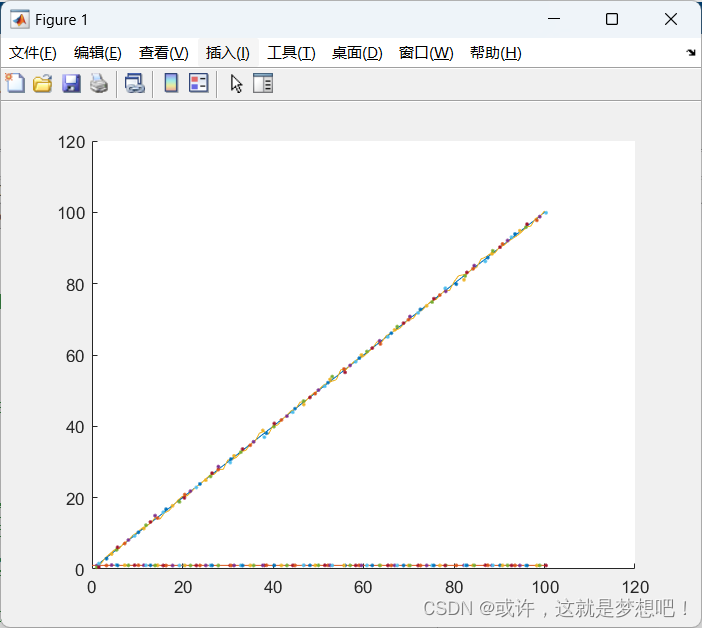
卡尔曼滤波算法的matlab实现

卡尔曼滤波算法的matlab实现 figure; hold on;Z(1:1:100); %观测值&#xff1a;第一秒观测1m 第二秒观测两米 匀速运动, 每秒1m, 最后拟合的也是速度 1m/splot(Z); plot([0,100], [1,1]);noiserandn(1,100)*0.5; %生成方差为1的高斯噪声 ZZnoise; % 加入噪声plot(Z);X[0;…...

编程日记 2024/6/4 17:58:02

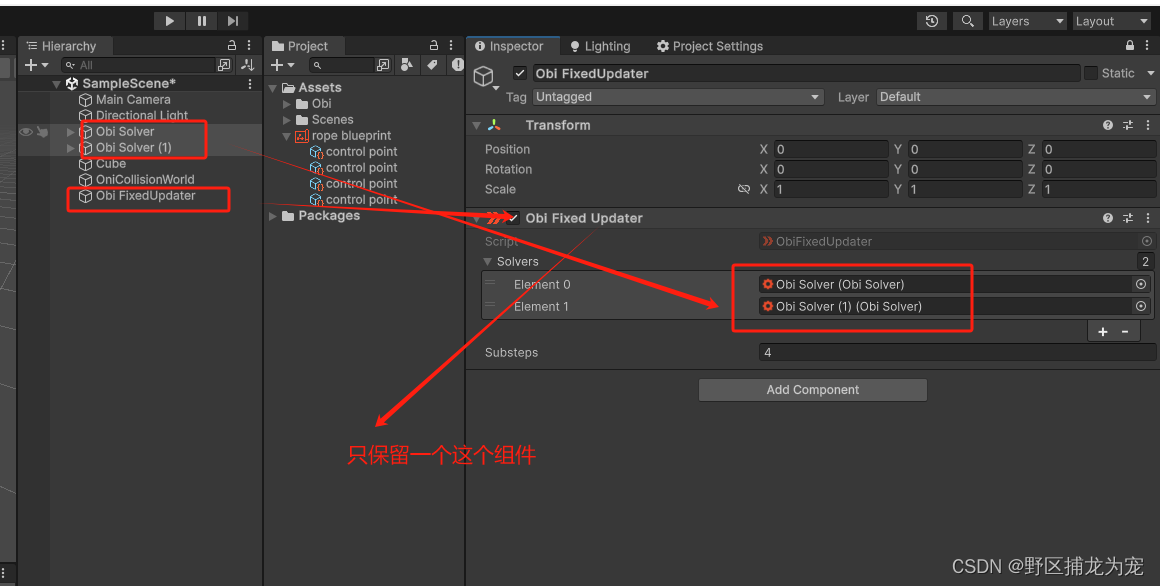
Unity Obi Rope失效

文章目录 前言一、WebGL端Obi Rope失效二、Obi Rope 固定不牢三、使用Obi后卡顿总结 前言 Obi 是一款基于粒子的高级物理引擎&#xff0c;可模拟各种可变形材料的行为。 使用 Obi Rope&#xff0c;你可以在几秒内创建绳索和杆子&#xff0c;同时完全控制它们的形状和行为&…...

编程日记 2024/6/4 17:57:01

Linux链表操作全解析

Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表&#xff1f;1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

编程新知 2025/12/3 20:14:32

Golang 面试经典题：map 的 key 可以是什么类型？哪些不可以？

Golang 面试经典题&#xff1a;map 的 key 可以是什么类型&#xff1f;哪些不可以&#xff1f; 在 Golang 的面试中&#xff0c;map 类型的使用是一个常见的考点&#xff0c;其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

编程新知 2025/12/20 7:42:02

Xshell远程连接Kali（默认 | 私钥）Note版

前言:xshell远程连接&#xff0c;私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

编程新知 2026/1/28 2:18:42

阿里云ACP云计算备考笔记 (5)——弹性伸缩

目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

编程新知 2026/1/22 6:07:24

大数据零基础学习day1之环境准备和大数据初步理解

学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 &#xff08;1&#xff09;设置网关 打开VMware虚拟机&#xff0c;点击编辑…...

编程新知 2026/1/25 14:43:07

Objective-C常用命名规范总结

【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名&#xff08;Class Name)2.协议名&#xff08;Protocol Name)3.方法名&#xff08;Method Name)4.属性名&#xff08;Property Name&#xff09;5.局部变量/实例变量&#xff08;Local / Instance Variables&…...

编程新知 2025/12/14 22:33:06

C# 类和继承(抽象类)

抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

编程新知 2026/1/29 16:25:24

Robots.txt 文件

什么是robots.txt&#xff1f; robots.txt 是一个位于网站根目录下的文本文件&#xff08;如&#xff1a;https://example.com/robots.txt&#xff09;&#xff0c;它用于指导网络爬虫&#xff08;如搜索引擎的蜘蛛程序&#xff09;如何抓取该网站的内容。这个文件遵循 Robots…...

编程新知 2025/9/9 5:38:23

C++.OpenGL （10/64）基础光照（Basic Lighting）

基础光照（Basic Lighting） 冯氏光照模型（Phong Lighting Model） #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

编程新知 2026/1/20 2:37:04

NFT模式：数字资产确权与链游经济系统构建

NFT模式&#xff1a;数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新&#xff1a;构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议&#xff1a;基于LayerZero协议实现以太坊、Solana等公链资产互通&#xff0c;通过零知…...

编程新知 2026/1/31 23:23:23