一、向量及其线性运算
🙌作者简介:数学与计算机科学学院出身、在职高校高等数学专任教师,分享学习经验、生活、 努力成为像代码一样有逻辑的人!
🌙个人主页:阿芒的主页
⭐ 高等数学专栏介绍:本专栏系统地梳理高等数学这门课的知识点,参考书主要为经典的同济版第七版《高等数学》以及作者在高校使用的《高等数学》系统教材。梳理《高等数学》这门课,旨在帮助那些刚刚接触这门课的小白以及需要系统复习这门课的考研人士。希望自己的一些经验能够帮助更多的人。
文章目录
- 向量的概念
- 向量的线性运算
- 空间直角坐标系
向量的概念
向量: 既有大小又有方向的量(又称矢量)
表示法: 有向线段 M1M2→\overrightarrow{M_1M_2}M1M2 或a→\overrightarrow{a}a
向径(矢径): 起点为原点的向量
自由向量: 与起点无关的向量
向量的模: 向量的大小,记作 ∣M1M2→∣|\overrightarrow{M_1M_2}|∣M1M2∣ 或∣a→∣|\overrightarrow{a}|∣a∣
单位向量: 模为1的向量
零向量: 模为0的向量,记作 0→\overrightarrow{0}0,或0
向量相等: 若向量a→\overrightarrow{a}a与b→\overrightarrow{b}b 大小相等,方向相同,记作a→=b→\overrightarrow{a}=\overrightarrow{b}a=b
负向量: 与 模相同,方向相反向量,记作 −a→-\overrightarrow{a}−a
向量共线: 由于平行向量可平移到同一直线上,故两向量平行又称两向量共线.
向量共面: 若 k(≥3)k(\geq 3)k(≥3)个向量经平移可移到同一平面上,则称此 kkk个向量共面.
向量的线性运算
-
向量的加法
运算法则: 满足平行四边形法则和三角形法则
注:三角形法则可推广到多个向量相加
运算规律:
①交换律 a→+b→=b→+a→\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}a+b=b+a
②结合律(a→+b→)+c→=a→+(b→+c→)(\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})(a+b)+c=a+(b+c) -
向量的减法
运算法则: 满足三角形法则
注:三角不等式关系(由三角形边长关系可证) -
向量的数乘
λ{\lambda}λ是一个数,λ{\lambda}λ与 a→\overrightarrow{a}a的乘积是一个新向量,记作 λa→\lambda\overrightarrow{a}λa
规定:λ>0{\lambda>0}λ>0时,λa→\lambda\overrightarrow{a}λa与a→\overrightarrow{a}a同向,∣λa→∣|\lambda\overrightarrow{a}|∣λa∣=λ∣a→∣\lambda|\overrightarrow{a}|λ∣a∣;
~~~~~~~~~ λ<0{\lambda<0}λ<0时,λa→\lambda\overrightarrow{a}λa与a→\overrightarrow{a}a反向,∣λa→∣|\lambda\overrightarrow{a}|∣λa∣=-λ∣a→∣\lambda|\overrightarrow{a}|λ∣a∣;
~~~~~~~~~ λ=0{\lambda=0}λ=0时,λa→\lambda\overrightarrow{a}λa=0→\overrightarrow{0}0.
总之:∣λa→∣|\lambda\overrightarrow{a}|∣λa∣=∣λ∣∣a→∣|\lambda||\overrightarrow{a}|∣λ∣∣a∣
运算规律:
①结合律:λ(μ)a→\lambda(\mu)\overrightarrow{a}λ(μ)a=μ(λa→)\mu(\lambda\overrightarrow{a})μ(λa)=λμa→\lambda\mu\overrightarrow{a}λμa
②分配律:(λ+μ)a→(\lambda+\mu)\overrightarrow{a}(λ+μ)a=λa→+μa→\lambda\overrightarrow{a}+\mu\overrightarrow{a}λa+μa
~~~~~~~~~~~~~~~ λ(a→+b→)\lambda(\overrightarrow{a}+\overrightarrow{b})λ(a+b)=λa→+λb→\lambda\overrightarrow{a}+\lambda\overrightarrow{b}λa+λb
注:若a→≠0→\overrightarrow{a}\neq\overrightarrow{0}a=0,则有单位向量a→°=a→∣a→∣\overrightarrow{a}^{°}=\frac{\overrightarrow{a}}{|\overrightarrow{a}|}a°=∣a∣a.因此a→\overrightarrow{a}a=∣a→∣|\overrightarrow{a}|∣a∣a→°\overrightarrow{a}^{°}a°
向量共线定理:设a→\overrightarrow{a}a为非零向量,则a→∥b→\overrightarrow{a}\parallel\overrightarrow{b}a∥b ⟺\Longleftrightarrow⟺b→\overrightarrow{b}b=λa→\lambda\overrightarrow{a}λa(λ\lambdaλ为唯一 实数).
空间直角坐标系
概念: 过空间一定点O,由三条互相垂直的数轴按右手规则组成一个空间直角坐标系.
构成: 坐标原点:O(0,0,0)
~~~~~~~~~~~ 坐标轴: x轴、y轴、z轴
~~~~~~~~~~~ 坐标面:xoy面、yoz面、xoz面
~~~~~~~~~~~ 卦限(八个)
卦限符号特征:
| 卦限 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ | Ⅶ | Ⅷ |
|---|---|---|---|---|---|---|---|---|
| x | + | - | - | + | + | - | - | + |
| y | + | + | - | - | + | + | - | - |
| z | + | + | + | + | - | - | - | - |
相关文章:

一、向量及其线性运算
🙌作者简介:数学与计算机科学学院出身、在职高校高等数学专任教师,分享学习经验、生活、 努力成为像代码一样有逻辑的人! 🌙个人主页:阿芒的主页 ⭐ 高等数学专栏介绍:本专栏系统地梳理高等数学…...

Spring Cloud/Spring Cloud Alibaba核心知识总结
Spring Cloud核心知识总结 springCloud是一个服务治理平台,若干个框架的集合,提供了全套的分布式系统的解决方案。包含:服务注册与发现、配置中心、服务网关、智能路由、负载均衡、断路器、监控跟踪、分布式消息、分布式事务等等。 SpringC…...
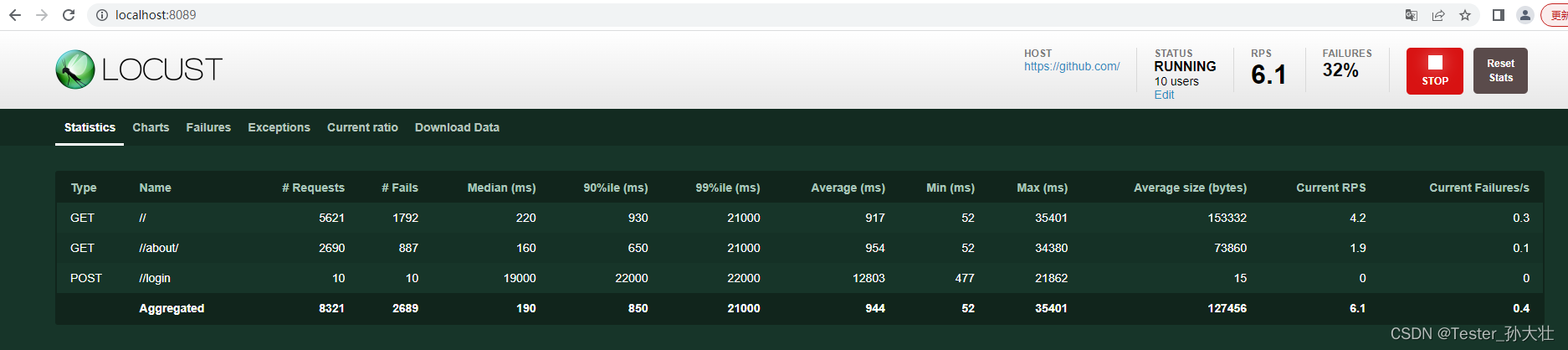
Locust框架从0到1入门
Locust介绍 Locust是使用Python语言编写实现的开源性能测试工具,可以用来测试Web应用程序、API、数据库等各种应用程序的性能,使用起来简洁、轻量、高效,并发机制基于gevent协程,可以实现单机模拟生成较高的并发压力。中文意为&a…...
表示范围)
C++:整数(short ,int,long,long long)表示范围
整形 C用short、int、long 、long long来表示整数的整形,同一整形也分为有符号(signed)和无符号(unsigned)两种。数据长度与操作系统和编译器的位数有关,其能够表示的范围也有所不同。接下来本文将用代码的…...
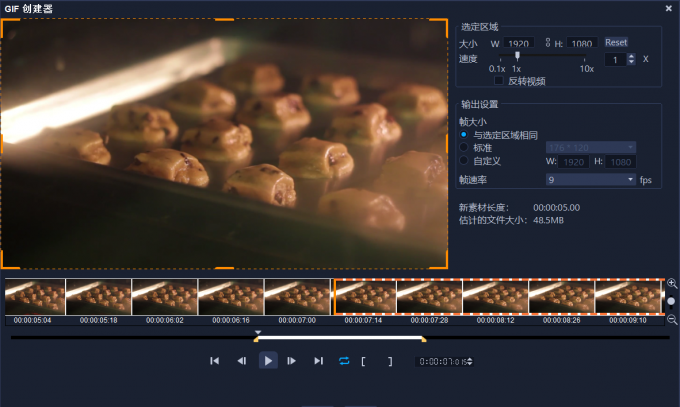
会声会影2023旗舰版新功能介绍,Corel VideoStudio Ultimate2023以及电脑系统配置要求
会声会影2023中文旗舰版功能非常强大的视频编辑软件,非常专业的使用效果,会声会影2023中文版可以针对剪辑电影进行使用,非常强大的色彩校正方式,无论什么光线下进行拍摄,都可以通过后期进行调整,并且里面超…...

软件测试用例篇(5)
测试是否运行代码去划分? 1)静态测试: 不运行代码,检查代码的风格,格式是否符合公司的标准规范,检查代码的逻辑结构是否满足需求要实现的功能 看代码,不运行代码,通过静态分析代码的语法,编写规…...

三个修饰符
三个修饰符三个修饰符一、abstract1.1 修饰类1.2 修饰方法二、final2.1 修饰类2.2 修饰方法2.3 修饰变量2.3.1 修饰属性2.3.2 修饰局部变量2.3.3 修饰方法的参数2.3.4 常量三、static关键字3.1 修饰属性3.2 修饰方法3.3 修饰代码块3.4 继承时的执行顺序三个修饰符 一、abstrac…...

JVM调优面试题——参数命令专题
文章目录1、JVM参数有哪些?1.1、 标准参数1.2、-X参数1.3、 -XX参数1.4、 其他参数1.5、 查看参数1.6、 设置参数的常见方式1.7、 常用参数含义2、JVM常用命令有哪些?2.1、jps2.2、jinfo2.3、jstat2.4、jstack2.5、jmap3、你会估算GC频率吗?4、 内存溢出…...
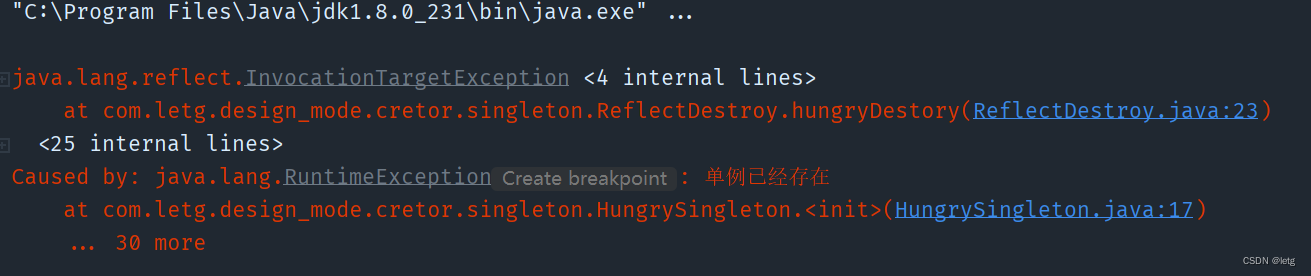
单例模式(设计模式详解)
单例模式 描述 单例模式是一种创建型模式,它的目的是确保一个类只有一个实例,并提供全局访问点。这个实例可以被多个客户端共享,从而避免创建多个实例所带来的资源浪费和不必要的复杂性。 实现 懒汉模式 public class LasySingleton {priv…...

设计一份关于文化遗产视频的调查问卷
参考文献:[1]任洁. 重庆美食类短视频传播策略研究[D].重庆交通大学,2021.DOI:10.27671/d.cnki.gcjtc.2021.000699.📰1 设计背景现已制作一些关于文化遗产的时长4-5分钟的视频,需要面向在校大学生收集他们对视频的看法从而分析视频的传播效果&…...
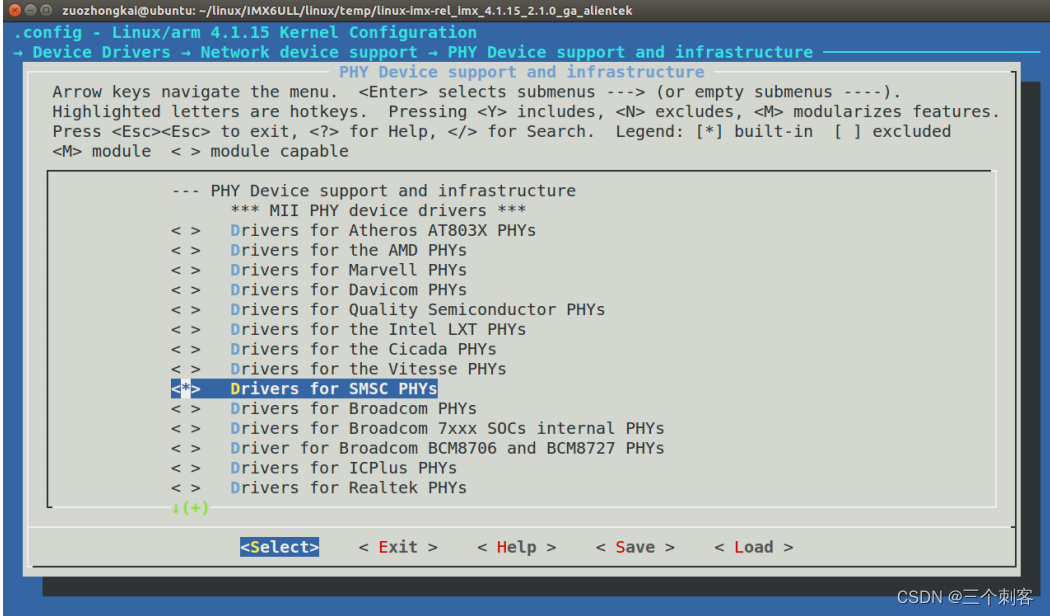
Linux内核移植
内核移植半导体厂商会从linux内核官网下载某个版本,将其移植到自己的CPU上,测试成功后就会将其开放给该半导体的厂商的CPU开发者,开发者下载其提供的linux内核,然后将其移植到自己的 产品上。1、NXP官方开发板Linux内核编译测试编…...

忆享科技优化入职培训加强人效管理全面迎接新挑战
-优化入职培训-忆享科技加强人效管理入职培训课程 ✦ KPI系统上线 ✦ 砥砺前行前言许多企业随着自身的不断发展,对于各类人才引进需求也越来越迫切,一批批新员工的加入,公司规模逐渐扩大,给公司带来了全新的血液。但在大量新员工加…...
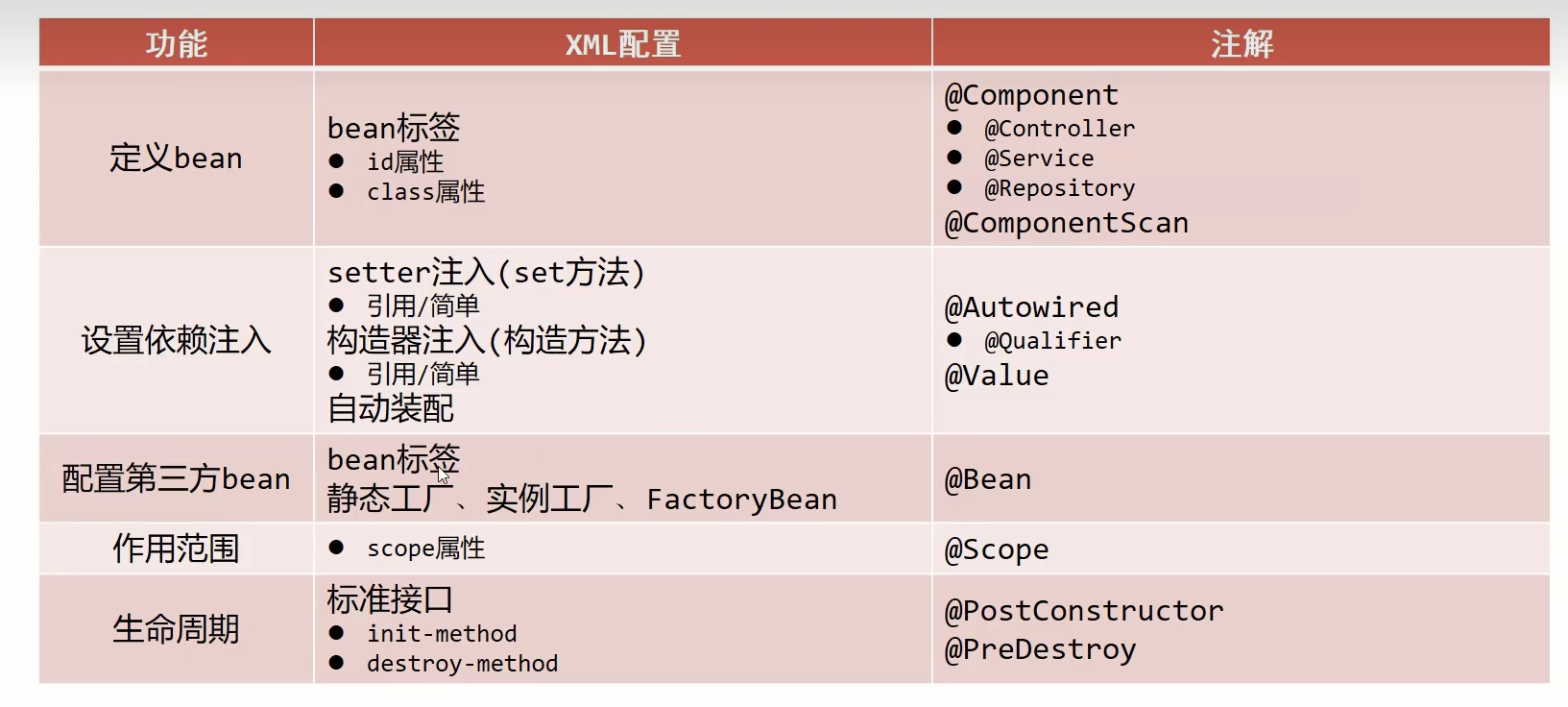
Spring——注解开发依赖注入和管理第三方bean
自动装配(引用类型) 环境准备: 文件结构如下图所示,Dao层的实现类里面有一个save方法,Service层里面的实现类有一个BookDao的声明和一个set方法,同时也有一个save方法,配置类的扫描范围如图所示 在当前的一个测试类当…...
)
shell可能考你但是不常用的基础($篇)
前言 当你面试的时候,可能要说的架构什么都准备好了,也说的七七八八,结果到最后问了一些基础的问题答不上来或者没想起来就很容易造成社会性死亡,一个没答上来道心被破,后面就更容易懵逼了 通常造成这个问题的原因是写…...

项目管理必备:如何绘制一份优秀的甘特图?
本文一共分为两部分—— 分享60Excel甘特图模板,简单省事儿分享两种甘特图制作教程,高效快捷 第一部分——60甘特图模板 分享一些项目管理甘特图的模板,省事儿!高效!简单! Excel甘特图表模板自取…...
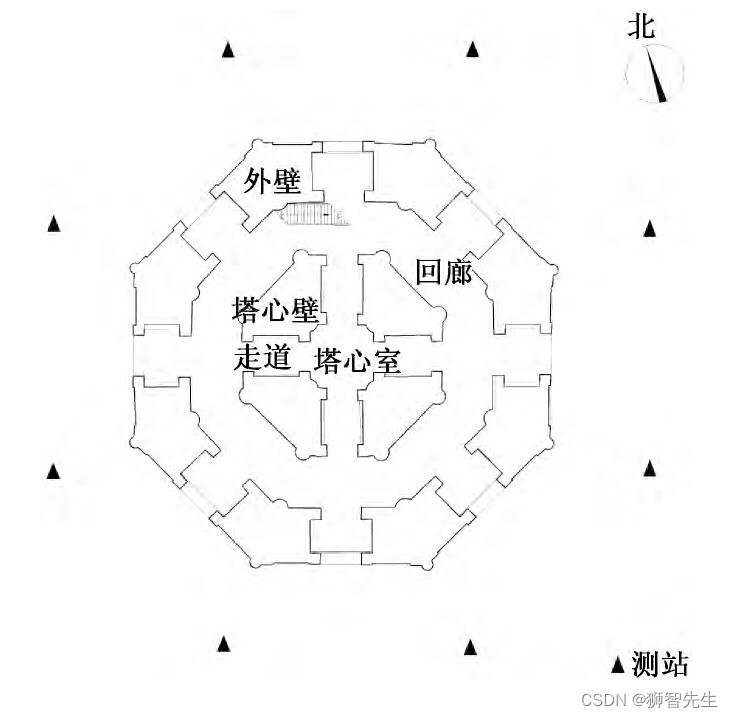
【点云学习】多时相激光雷达点云
多时相雷达数据(multi-tempral LiDAR data) 1 一种多时相激光雷达数据建筑物变化检测方法-汪承义(2013) 背景:空间分辨率的提高引入了“类内可分性”增加与“类间可分性”降低;遮挡与阴影的存在使问题变得…...

使用QT C++编写一个随机生成网络ip地址的程序
根据网络搜索结果,使用QT C编写一个随机生成网络ip地址的程序的示例代码可能如下: cpp #include <QCoreApplication> #include <QRandomGenerator> #include <QDebug> int main(int argc, char *argv[]) { QCoreApplication a(a…...

Web前端学习:章三 -- JavaScript预热(三)
六九:函数的变量提升 函数的变量提升没有var高,var是最高的。 先提var,再提函数 解析: 1、4行打印之前没有定义变量,预解析触发变量提升 2、先提var,再提函数。所以先把var提升到最上面,然后提…...

java实用小技巧:判断list是否有重复项
在项目中经常会遇到这样的场景,就是一个list,根据某种规则,我要去判断里面是不是有重复的项。 难度不高,但有点烦,所以专门开一篇文章来记录一下,争取弄一个相对简洁的写法。 先看一个简单的例子…...
)
SQL优化常用招数(上)
文章目录 一、查询SQL尽量不要使用select *,而是具体字段二、避免在where子句中使用 or 来连接条件三、尽量使用数值替代字符串类型四、使用varchar代替char五、技术延伸,char与varchar2的区别?六、where中使用默认值代替null七、避免在where子句中使用!=或<>操作符八…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
